Matrices Orthogonal matrix When the product of a


















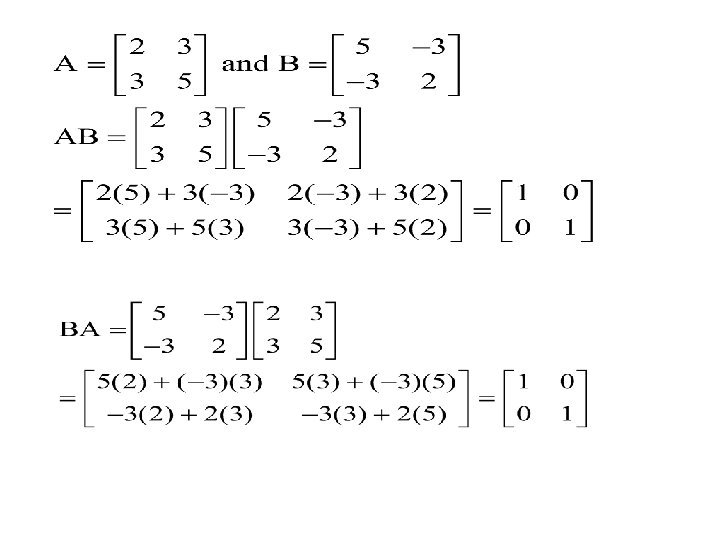
































- Slides: 52

Matrices









Orthogonal matrix When the product of a matrix A with its transposed matrix is a unit matrix ; then the matrix A is called an orthogonal matrix.

Conjugate of a matrix The complex matrix obtained from any given matrix A on replacing its elements by the corresponding conjugate complex numbers is called the conjugate matrix.

Trensposed Conjugate of a matrix The transpose of the conjugate of a matrix A is called Transposed Conjugate of a matrix.

Hermitian matrix A square matrix A is said to be Hermitian matrix if it is equal to its conjugate transposed matrix

Skew-Hermitian matrix A square matrix A is said to be Skew-Hermitian matrix if it is equal to the minus of its conjugate transposed matrix

Unitary matrix A square matrix A is said to be Unitary matrix if the product of A to its conjugate transposed matrix is equal to the Identity matrix



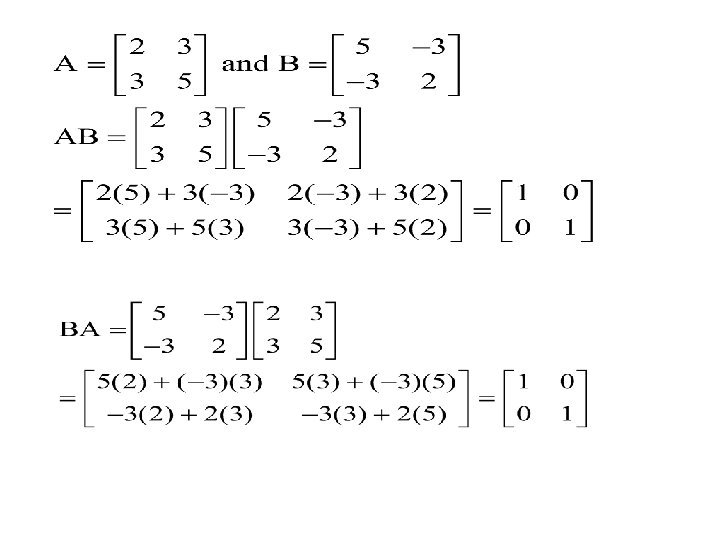



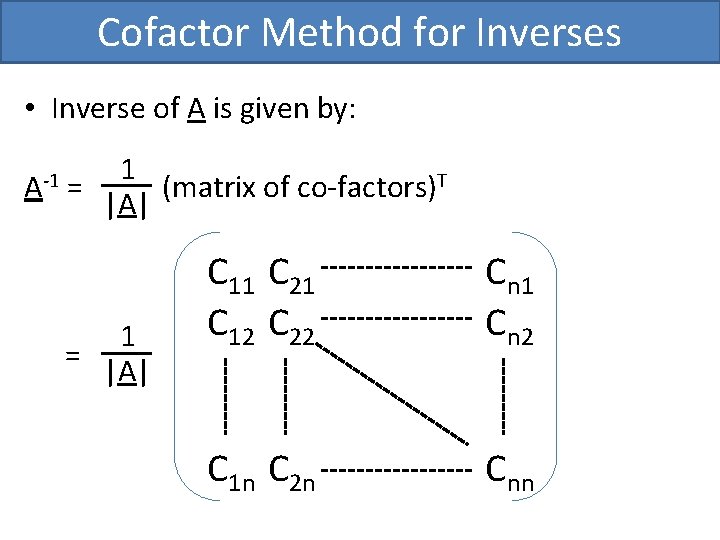
Cofactor Method for Inverses • Let A = (aij) be an nxn matrix • Recall, the co-factor Cij of element aij is: Cij = (-1)i+j |Mij| • Mij is the (n-1) x (n-1) matrix made by removing the ROW i and COLUMN j of A

Cofactor Method for Inverses • Inverse of A is given by: A-1 1 = (matrix of co-factors)T |A| 1 = |A| C 11 C 21 C 12 C 22 Cn 1 Cn 2 C 1 n C 2 n Cnn

Examples • Calculate the inverse of A = M 11 = d |M 11| = d a b c d C 11 = d

Examples • Calculate the inverse of A = M 12 = c |M 12| = c a b c d C 12 = -c

Examples • Calculate the inverse of A = M 21 = b |M 21| = b a b c d C 12 = -b

Examples • Calculate the inverse of A = M 22 = a |M 22| = a a b c d C 22 = a

Examples • Calculate the inverse of A = a b c d • Found that: C 11 = d C 12 = -c C 21 = -b C 22 = a • So, A-1 1 = (matrix of co-factors)T |A|

Examples • Calculate the inverse of A = a b c d • Found that: C 11 = d C 12 = -c C 21 = -b C 22 = a • So, A-1 1 = (matrix of co-factors)T (ad-bc)

Examples • Calculate the inverse of A = a b c d • Found that: C 11 = d C 12 = -c C 21 = -b C 22 = a • So, C 11 C 12 1 A-1 = (ad-bc) C C 21 22 T

Examples • Calculate the inverse of A = a b c d • Found that: C 11 = d C 12 = -c C 21 = -b C 22 = a • So, C 11 C 21 1 A-1 = (ad-bc) C C 12 22

Examples • Calculate the inverse of A = a b c d • Found that: C 11 = d C 12 = -c C 21 = -b C 22 = a • So, A-1 d -b 1 = (ad-bc) -c a

Examples 3 x 3 Matrix 1 • Calculate the inverse of B = 1 2 1 1 2 2 3 4 • Find the co-factors: 2 2 M 11 = 3 4 |M 11| = 2 C 11 = 2

Examples 3 x 3 Matrix 1 • Calculate the inverse of B = 1 2 1 1 2 2 3 4 • Find the co-factors: 1 2 M 12 = 2 4 |M 12| = 0 C 12 = 0

Examples 3 x 3 Matrix 1 • Calculate the inverse of B = 1 2 1 1 2 2 3 4 • Find the co-factors: 1 2 M 13 = 2 3 |M 13| = -1 C 13 = -1

Examples 3 x 3 Matrix 1 • Calculate the inverse of B = 1 2 1 1 2 2 3 4 • Find the co-factors: 1 1 M 21 = 3 4 |M 21| = 1 C 21 = -1

Examples 3 x 3 Matrix 1 • Calculate the inverse of B = 1 2 1 1 2 2 3 4 • Find the co-factors: 1 1 M 22 = 2 4 |M 22| = 2 C 22 = 2

Examples 3 x 3 Matrix 1 • Calculate the inverse of B = 1 2 1 1 2 2 3 4 • Find the co-factors: 1 1 M 23 = 2 3 |M 23| = 1 C 23 = -1

Examples 3 x 3 Matrix 1 • Calculate the inverse of B = 1 2 1 1 2 2 3 4 • Find the co-factors: 1 1 M 31 = 2 2 |M 31| = 0 C 31 = 0

Examples 3 x 3 Matrix 1 • Calculate the inverse of B = 1 2 1 1 2 2 3 4 • Find the co-factors: 1 1 M 32 = 1 2 |M 32| = 1 C 32 = -1

Examples 3 x 3 Matrix 1 • Calculate the inverse of B = 1 2 1 1 2 2 3 4 • First find the co-factors: 1 1 M 33 = 1 2 |M 33| = 1 C 33 = 1

Examples 3 x 3 Matrix 1 • Calculate the inverse of B = 1 2 1 1 2 2 3 4 • Next the determinant: use the top row: |B| = 1 x |M 11| -1 x |M 12| + 1 x |M 13| = 2 – 0 + (-1) = 1

Examples 3 x 3 Matrix • Using the formula, B-1 1 = (matrix of co-factors)T |B| 1 = (matrix of co-factors)T 1

Examples 3 x 3 Matrix • Using the formula, B-1 1 = (matrix of co-factors)T |B| 1 2 0 1 = 1 -1 2 -1 0 -1 1 = 2 -1 0 0 2 -1 -1 -1 1 T








 Perpendicular matrix
Perpendicular matrix Orthogonal matrices
Orthogonal matrices Orthogonal matrix properties
Orthogonal matrix properties Eigenvalue definition
Eigenvalue definition 3x3 orthogonal matrix
3x3 orthogonal matrix Orthogonal matrix
Orthogonal matrix Orthogonal similarity transformation
Orthogonal similarity transformation Properties of transpose of matrix
Properties of transpose of matrix Boolean product of zero-one matrices
Boolean product of zero-one matrices Ndc computer graphics
Ndc computer graphics Orthogonal set
Orthogonal set Orthogonal unit differentiation
Orthogonal unit differentiation Orthogonal polynomials examples
Orthogonal polynomials examples Orthogonal range searching
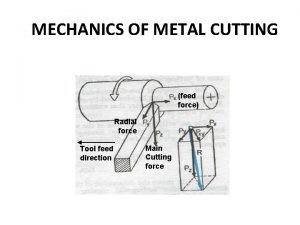
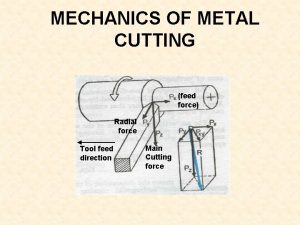
Orthogonal range searching Orthogonal cutting diagram
Orthogonal cutting diagram Orthonormal basis
Orthonormal basis Orthogonal views of software in ooad
Orthogonal views of software in ooad Merchant force circle diagram
Merchant force circle diagram Orthogonal iteration
Orthogonal iteration Orthogonal transformation in image processing
Orthogonal transformation in image processing Taguchi array selector
Taguchi array selector Orthogonal decomposition
Orthogonal decomposition Cauchy-schwarz inequality proof inner product
Cauchy-schwarz inequality proof inner product Orthogonal complement
Orthogonal complement Linear algebra
Linear algebra Fourier series orthogonality
Fourier series orthogonality Tool life in orthogonal cutting is mcq
Tool life in orthogonal cutting is mcq Pythagoras theorem for orthogonal set of vectors
Pythagoras theorem for orthogonal set of vectors Orthogonal hole phantom
Orthogonal hole phantom Feed in metal cutting
Feed in metal cutting Orthogonal projection in computer graphics
Orthogonal projection in computer graphics Orthogonal series expansion
Orthogonal series expansion Site:slidetodoc.com
Site:slidetodoc.com Orthogonal functions in fourier series
Orthogonal functions in fourier series Define orthonormal set with example
Define orthonormal set with example Orthogonal vectors
Orthogonal vectors Orthogonal array
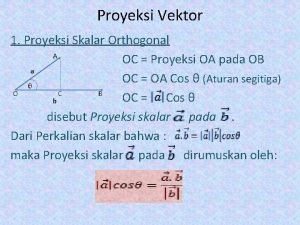
Orthogonal array Contoh proyeksi vektor
Contoh proyeksi vektor Orthogonal projection
Orthogonal projection Orthogonal
Orthogonal What are the two orthogonal view of software
What are the two orthogonal view of software Orthogonal frequency division multiplexing
Orthogonal frequency division multiplexing Channel
Channel Orthogonal cutting is dimensional metal cutting
Orthogonal cutting is dimensional metal cutting Fourier series and orthogonal functions
Fourier series and orthogonal functions First order linear differential equation
First order linear differential equation Hát kết hợp bộ gõ cơ thể
Hát kết hợp bộ gõ cơ thể Lp html
Lp html Bổ thể
Bổ thể Tỉ lệ cơ thể trẻ em
Tỉ lệ cơ thể trẻ em Voi kéo gỗ như thế nào
Voi kéo gỗ như thế nào Tư thế worm breton là gì
Tư thế worm breton là gì Chúa sống lại
Chúa sống lại