Math 307 Spring 2003 Hentzel Time 1 10




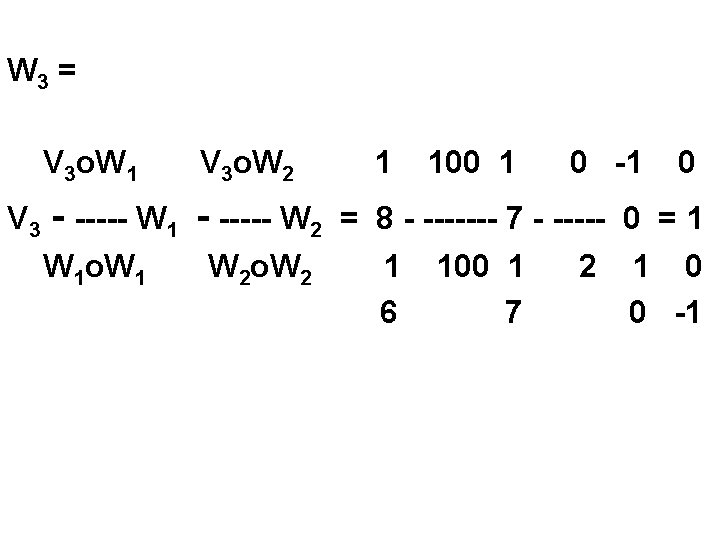
![Basis 1 -1 0 1/10 7 1/Sqrt[2] 0 1/Sqrt[2] 1 1 1 0 7 Basis 1 -1 0 1/10 7 1/Sqrt[2] 0 1/Sqrt[2] 1 1 1 0 7](https://slidetodoc.com/presentation_image_h/fde26ef1e9c199695c7d205789e95d46/image-6.jpg)

![| 1/10 -1/Sqrt[2] 0 || 10 10 10 | | 1 0 1 | | 1/10 -1/Sqrt[2] 0 || 10 10 10 | | 1 0 1 |](https://slidetodoc.com/presentation_image_h/fde26ef1e9c199695c7d205789e95d46/image-8.jpg)








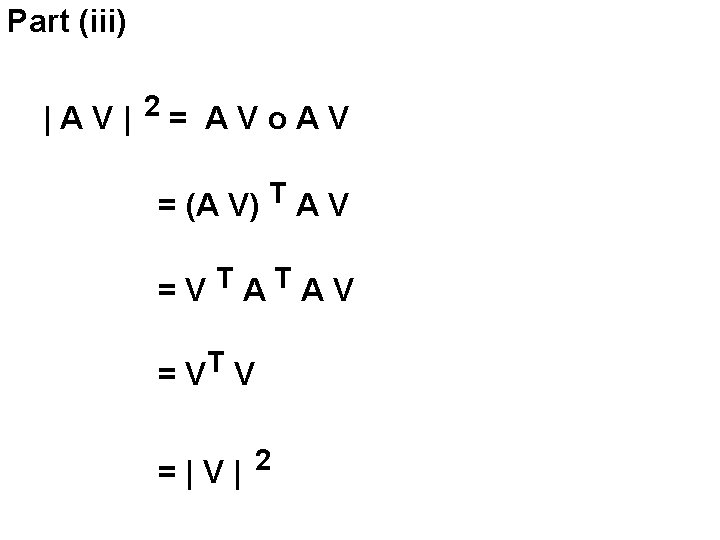






- Slides: 23

Math 307 Spring, 2003 Hentzel Time: 1: 10 -2: 00 MWF Room: 1324 Howe Hall Instructor: Irvin Roy Hentzel Office 432 Carver Phone 515 -294 -8141 E-mail: hentzel@iastate. edu http: //www. math. iastate. edu/hentzel/class. 307. ICN Text: Linear Algebra With Applications, Second Edition Otto Bretscher

Monday, March 24 Chapter 5. 3 Page 209 Problems 2, 6, 8, 12, 34 Main Idea: Orthonormal vectors make Orthogonal matrices. Key Words: QR-Factorization, (A B)T = BT AT, Transpose, Vo. W = V T W = WT V. Goal: Learn about orthogonal matrices and the matrix of orthogonal projections.

Previous Assignment Page 199 Problem 14 Using paper and pencil, perform the Gram. Schmidt process on the sequences of vectors given in Exercises 1 through 14. 1 7 V 1 0 7 2 7 V 2 1 8 1 6 V 3

W 1 = V 1 = 1 7 V 2 o. W 1 0 100 1 -1 W 2 = V 2 - ----- W 1 = 7 - --- 7 = 0 W 1 o. W 1 2 100 1 1 7 7 0
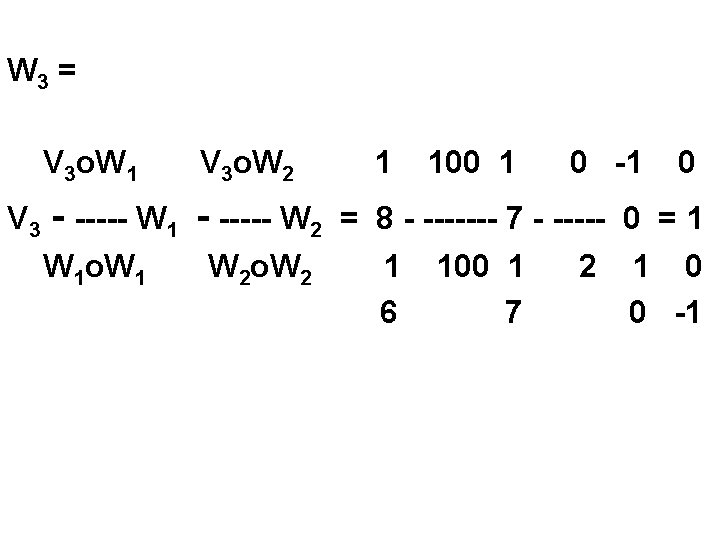
W 3 = V 3 o. W 1 V 3 o. W 2 - ----- W 1 - ----- W 2 W 1 o. W 1 W 2 o. W 2 1 100 1 0 -1 0 = 8 - ------- 7 - ----- 0 = 1 1 100 1 2 1 0 6 7 0 -1
![Basis 1 1 0 110 7 1Sqrt2 0 1Sqrt2 1 1 1 0 7 Basis 1 -1 0 1/10 7 1/Sqrt[2] 0 1/Sqrt[2] 1 1 1 0 7](https://slidetodoc.com/presentation_image_h/fde26ef1e9c199695c7d205789e95d46/image-6.jpg)
Basis 1 -1 0 1/10 7 1/Sqrt[2] 0 1/Sqrt[2] 1 1 1 0 7 0 -1

Page 199 Problem 28 Using paper and pencil, find the QR factorizations of the matrices in Exercises 15 through 28.
![110 1Sqrt2 0 10 10 10 1 0 1 | 1/10 -1/Sqrt[2] 0 || 10 10 10 | | 1 0 1 |](https://slidetodoc.com/presentation_image_h/fde26ef1e9c199695c7d205789e95d46/image-8.jpg)
| 1/10 -1/Sqrt[2] 0 || 10 10 10 | | 1 0 1 | | 7/10 0 1/Sqrt[2] || 0 Sqrt[2] 0 | = | 7 7 8 | | 1/10 1/Sqrt[2] 0 || 0 0 Sqrt[2]| | 1 2 1 | | 7/10 0 -1/Sqrt[2] || 0 0 0 | | 7 7 6|

Page 199 Problem 40 Consider an invertible nxn matrix A whose columns are orthogonal, but not necessarily orthonormal. What does the QR Factorization of A look like?

Since A is invertible, the columns of A are non zero. If A = [ C 1 C 2. . Cn ] of lengths d 1, d 2, . . . dn then

A is invertible, the columns of A are nonzero. If A = [ C 1 C 2. . Cn ] of lengths d 1, d 2, . . . dn then | d 1 | | d 2 | |. | A = [1/d 1 C 1 1/d 2 C 2. . . 1/dn Cn ] |. | | dn|

Vectors V 1 V 2. . . Vn are orthonormal if Vi o Vj = 0 for i =/= j and Vi o Vi = 1 for all i. Then nxn matrix is called orthogonal if its columns are orthonormal vectors.

Properties of orthogonal matrices. (i) AT A = A AT = I (ii) A -1 = A T (iii) | A V | = | V | A preserves lengths. (iv) If A and B are orthogonal, then AB is orthogonal. -1 (v) If A is orthogonal, then A is orthogonal. Proof: Suppose [V 1 V 2. . . Vn ] is an orthogonal matrix.


We show Part (i). This is just the statement that Vi o Vj = 0 if i =/= j and Vi o Vi = 1 for all i. This shows that A T A = I. But then A T is A -1 and so it works on the other side as well giving A A T = I.

Part (ii) is a consequence of Part (i).
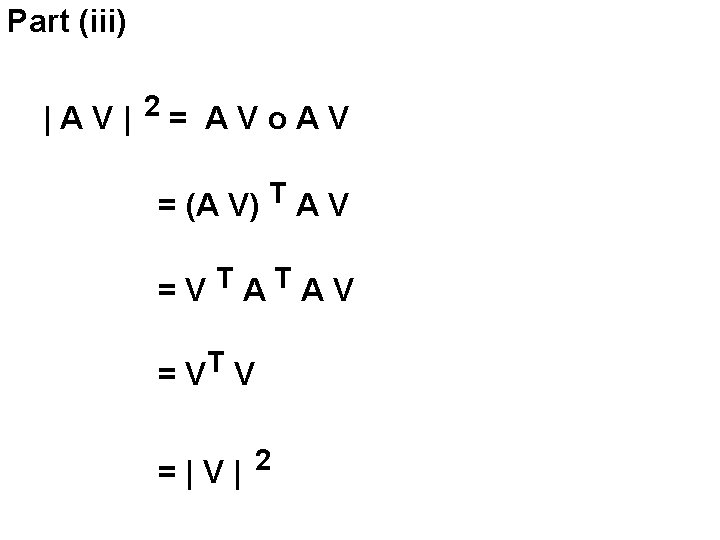
Part (iii) |AV| 2= AVo. AV T = (A V) A V T T =V A AV = VT V =|V| 2

Part (iv) If A and B are orthogonal, then (AB) T (AB) = B T A B = I. Thus the columns of AB are also orthonormal.

T Part (v) If A is orthogonal, then A A = I and so T the columns of A are also orthonormal.

The matrix of an orthogonal projection. n Consider a subspace V or R with orthonormal basis V 1, V 2. . . Vm. The matrix of the orthogonal projection onto V is |. . . | T A A where A = | V 1 V 2. . . Vm | |. . . |

Page 209 Example 7. Find the matrix of the orthogonal projection onto the subspace of R 4 spanned by ½ |1| |1| | 1| ½ | -1 | | 1|

