Sect 4 2 Orthogonal Transformations For convenience change

Sect. 4. 2: Orthogonal Transformations • For convenience, change of notation: x x 1, y x 2, z x 3, x´ x 1 , y´ x 2 , z´ x 3 aij cosθij • In new notation, transformation eqtns between primed & unprimed coords become: x 1 = a 11 x 1+a 12 x 2 +a 13 x 2 = a 21 x 1+a 22 x 2 +a 23 x 3 = a 31 x 1+a 32 x 2 +a 33 x 3 Or: xi = ∑j aij xj (i, j = 1, 2, 3) (1) • (1) = An example of what mathematicians call a Linear (or Vector) Transformation. Also:

• For convenience, another change of notation: If the index is repeated, summation over it is implied. xi = ∑j aij xj (i, j = 1, 2, 3) xi = aij xj (i, j = 1, 2, 3) Einstein summation convention • To avoid possible ambiguity when powers of an indexed quantity occur: ∑i(xi)2 xixi • For the rest of the course, summation convention is automatically assumed, unless stated otherwise.

• Linear Transformation: xi = aij xj (i, j = 1, 2, 3) (1) • With aij cosθij as derived, (1) is only a special case of a general linear transformation, since, as already discussed, the direction cosines cosθij are not all independent. – Re-derive connections between them, use new notation. • Both coord systems are Cartesian: Square of magnitude of vector = sum of squares of components. Magnitude is invariant on transformation of coords: xi xi = xixi Using (1), this becomes: aijaikxjxk = xixi (i, j, k = 1, 2, 3)

• aijaikxjxk = xixi (i, j, k = 1, 2, 3) Can be valid if & only if aijaik = δj, k (j, k = 1, 2, 3) Identical previous results for orthogonality of direction cosines. • Any Linear Transformation: xi = aij xj (i, j = 1, 2, 3) (1) Orthogonal Transformation aijaik = δj, k Orthogonality Condition

• Linear (or Vector) Transformation. xi = aijxj (i, j = 1, 2, 3) (1) • Can arrange direction cosines into a square matrix: A a 11 a 12 a 13 a 21 a 22 a 23 a 31 a 32 a 33 • Consider coordinate axes as column vector components: r = x 1 x 2 x 3 r = x 1 x 2 Coordinate transformation reln can be written: r = Ar with A Transformation matrix or rotation matrix (or tensor)

Example: 2 d Coordinate Rotation • Application to 2 d rotation. See figure: • Easy to show that: x 3 = x 3 x 1 = x 1 cos + x 2 sin = x 1 cos + x 2 cos( - π/2) x 2 = -x 1 sin + x 2 cos = x 1 cos( + π/2) + x 2 cos

• 2 d rotation. See fig: aij cosθij a 33 = cosθ 33 = 1 a 11 = cosθ 11 = cos a 22 = cosθ 22 = cos a 12 = cosθ 12 = cos( - π/2) = sin a 21 = cosθ 21 = cos( + π/2) = -sin a 31 = cosθ 31 = cos(π/2) = 0, a 32 = cosθ 32 = cos(π/2) = 0 Transformation matrix has form: a 11 a 12 0 cos sin 0 A= a 21 a 22 0 = -sin cos 0 0 0 1

• 2 d rotation. See fig: aij cosθij Orthogonality Condition: aijaik = δj, k a 11 + a 21 = 1 a 12 + a 22 = 1 , a 11 a 12 + a 21 a 22 = 0 Use expressions for aij & get: cos 2 + sin 2 =1 sin 2 + cos 2 =1, cos sin - sin cos = 0 Need only one angle to specify a 2 d rotation.

• Transformation matrix A Math operator that, acting on unprimed system, transforms it to primed system. Symbolically: r = Ar (1) Matrix A, acting on components of the r in unprimed system yields components of r in the primed system. • Assumption: Vector r itself is unchanged (in length & direction) on operation with A. (r 2 = (r )2) • NOTE: Same formal mathematics results from another interpretation of (1): A acts on r & changes it into r . Components of 2 vectors related by (1). • Which interpretation depends on context of problem. Usually, for rigid body motion, use 1 st interpretation. • For general transformation (1), nature of A depends on which interpretation is used. A acting on coords: Passive transformation. A acting on vector: Active transformation

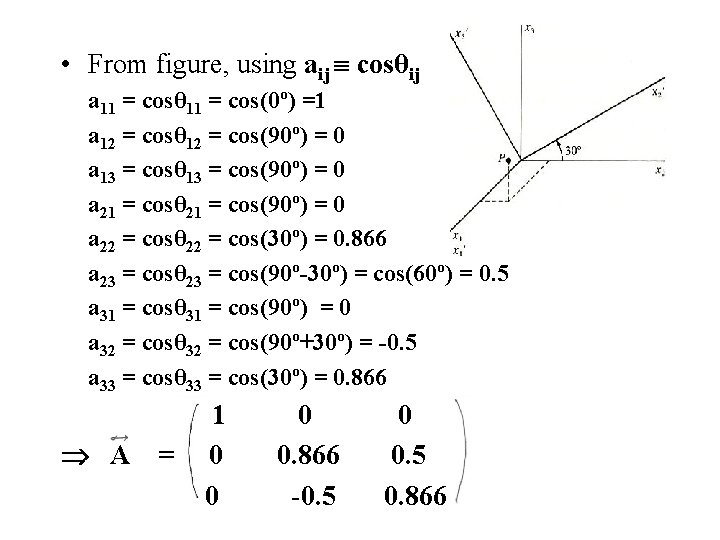
Example from Marion • In the unprimed system, point P is represented as (x 1, x 2, x 3) = (2, 1, 3). In the primed system, x 2 has been rotated from x 2, towards x 3 by a 30º angle as in the figure. Find the rotation matrix A & the representation of P = (x 1 , x 2 , x 3 ) in the primed system.

• From figure, using aij cosθij a 11 = cosθ 11 = cos(0º) =1 a 12 = cosθ 12 = cos(90º) = 0 a 13 = cosθ 13 = cos(90º) = 0 a 21 = cosθ 21 = cos(90º) = 0 a 22 = cosθ 22 = cos(30º) = 0. 866 a 23 = cosθ 23 = cos(90º-30º) = cos(60º) = 0. 5 a 31 = cosθ 31 = cos(90º) = 0 a 32 = cosθ 32 = cos(90º+30º) = -0. 5 a 33 = cosθ 33 = cos(30º) = 0. 866 A = 1 0 0. 866 -0. 5 0. 866

• To find new representation of P, apply r = Ar or x 1 = a 11 x 1+a 12 x 2 +a 13 x 2 = a 21 x 1+a 22 x 2 +a 23 x 3 = a 31 x 1+a 32 x 2 +a 33 x 3 Using (x 1, x 2, x 3) = (2, 1, 3) x 1 = 2 x 2 = 0. 866 x 2 +0. 5 x 3 = 2. 37 x 3 = -0. 5 x 2 + 0. 866 x 3 = 2. 10 (x 1 , x 2 , x 3 ) = (2, 2. 37, 2. 10)

Useful Relations • Consider a general line segment, as in the figure: Angles α, β, γ between the segment & x 1, x 2, x 3 Direction cosines of line cosα, cosβ, cosγ Manipulation, using orthogonality relns from before: cos 2α + cos 2β + cos 2γ = 1

• Consider 2 line segments, direction cosines, as in the figure: cosα, cosβ, cosγ, & cosα , cos β , cosγ • Angle θ between segments: • Manipulation (trig): cosθ = cosα +cosβ +cosγ

Sect. 4. 3: Formal (math) Properties of the Transformation Matrix • For a while (almost) pure math! • 2 successive orthogonal transformations B and A, acting on unprimed coordinates: r = Br followed by r = Ar = ABr • In component form, application of B followed by A gives (summation convention assumed, of course!): xk = bkjxj , xi = aikxk = aikbkjxj (1) (i, j, k = 1, 2, 3) xi = cijxj (2) • (2) has the form of an orthogonal transformation C AB with elements of the square matrix C given by cij aikbkj Rewrite (1) as:

Products Product of 2 orthogonal transformations B (matrix elements bkj) & A (matrix elements aik) is another orthogonal transformation C = AB (matrix elements cij aikbkj). – Proof that C is also orthogonal: See Prob. 1, p 180. • Can show (student exercise!): Product of orthogonal transformations is not commutative: BA AB – Define: D BA (matrix elements dij bikakj). Find, in general: dij cij. Final coords depend on order of application of A & B. • Can also show (student exercise!): Products of such transformations are associative: (AB)C = A(BC)

• Note: Text now begins to use vector r & vector x interchangeably! r = Ar x = Ax can be represented in terms of matrices, with coord vectors being column vectors: x = Ax xi = aijxj or: x 1 a 12 a 13 x 1 x 2 = a 21 a 22 a 23 x 2 a 31 a 32 a 33 x 3 • Addition of 2 transformation matrices: C = A + B Matrix elements are: cij = aij + bij

Inverse • Define the inverse A-1 of transformation A: x = Ax (1), x A-1 x (2) In terms of matrix elements, these are: xk = akixi (1 ), xi aij xj (2 ) where aij are matrix elements of A-1 • Combining (1 ) & (2 ): xk = akiaij xj clearly, this can hold if & only if: akiaij = δj, k (3 ) Define: Unit Matrix 1 0 0 1 0 akiaij = δj, k are clearly matrix 0 0 1 elements of 1

Transpose In terms of matrices, DEFINE A-1 by: AA-1 A-1 A 1 – Proof that AA-1 A-1 A : p 146 of text. • 1 Identity transformation because: x = 1 x and A = 1 A • Matrix elements of A-1 & of A are related by: aij = aji (4) – Proof of this: p 146 -147 of text. • Define: Ã Transpose of A matrix obtained from A by interchanging rows & columns. Clearly, (4) A-1 = Ã & thus: ÃA = AÃ = 1

A-1 = Ã For orthogonal matrices, the reciprocal is equal to the transpose. • Combine aij = aji with akiaij = δj, k akiaji = δj, k (5): A restatement of the orthogonality relns for the aki ! • Dimension of rectangular matrix, m rows, n columns m n. A, A-1, Ã : Square matrices with m = n. – Column vector (1 column matrix) x, dimension m 1. Transpose x: dimension 1 m (one row matrix). – Matrix multiplication: Product AB exists only if # columns of A = # rows of B: cij = aikbkj – See text about multiplication of x & its transpose with A & Ã

Define: • Symmetric Matrix A square matrix that is the same as its transpose: A = Ã aij = aji • Antisymmetric Matrix A square matrix that is the negative of its transpose: A = - Ã aij = - aji – Obviously, diagonal elements in this case: aii = 0

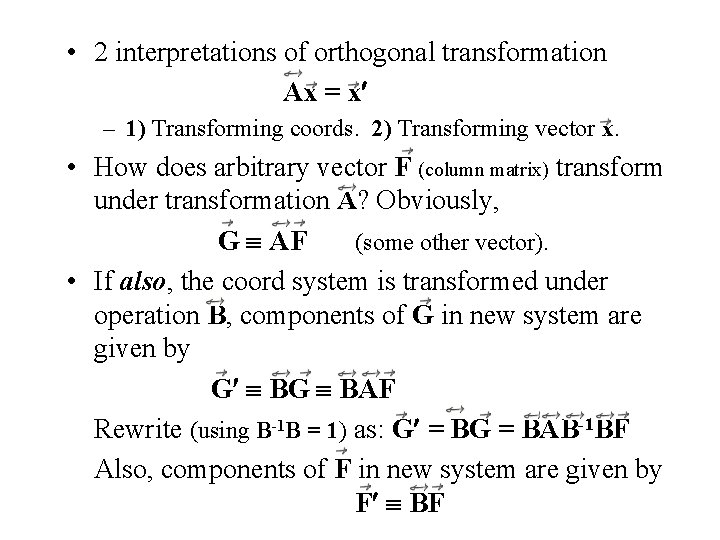
• 2 interpretations of orthogonal transformation Ax = x – 1) Transforming coords. 2) Transforming vector x. • How does arbitrary vector F (column matrix) transform under transformation A? Obviously, G AF (some other vector). • If also, the coord system is transformed under operation B, components of G in new system are given by G BAF Rewrite (using B-1 B = 1) as: G = BAB-1 BF Also, components of F in new system are given by F BF

• Combining gives: G = BAB-1 F where: F BF, G BG If define operator BAB-1 A we have: G A F (same form as G = AF, but expressed in transformed coords) Transformation of operator A under coord transformation B is given as: A BAB-1 Similarity transformation

• Properties of determinant formed from elements of an orthogonal transformation matrix: det(A) |A| Some identities (no proofs): • |AB| = |A||B| From orthogonality reln ÃA = AÃ = 1 get • |Ã||A| = |A||Ã| = 1 Determinant is unaffected by interchange of rows & columns: • |Ã| = |A| Using this with above gives: • |A|2 = 1 |A| = 1

• Value of determinant is invariant under a similarity transformation. Proof: A, B orthogonal transformations – Assumes 1) B-1 exists & 2) |B| 0 Similarity transformation: A BAB-1 Multiply from right by B: A B = BAB-1 B = BA Determinant: |A ||B| = |B||A| (|B| = a number 0) Divide by |B| on both sides & get |A | = |A|