7 Exploring Orthogonal Arrays 1 Construction of Orthogonal

第 7章 直交表深入探討 Exploring Orthogonal Arrays 1. 直交表的建構（Construction of Orthogonal Arrays） 2. 交互作用表的建構（Construction of Interaction Tables） 3. 近直交表實驗（Nearly Orthogonal Arrays）

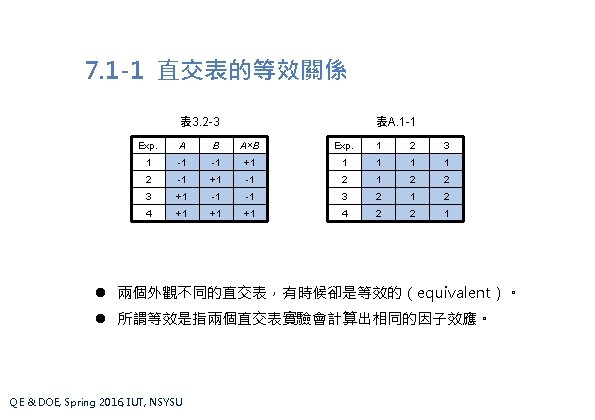
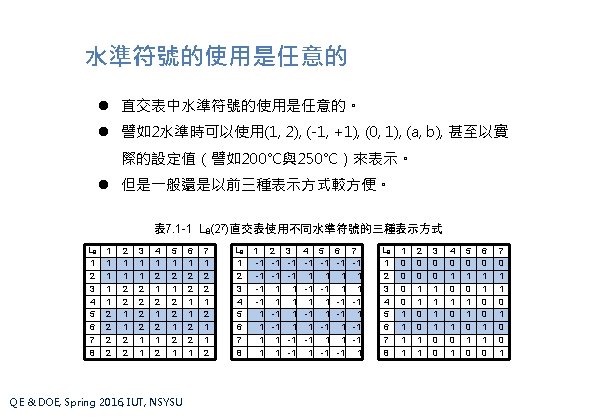
第 7. 1節 直交表的建構 Construction of Orthogonal Arrays 7. 1 -1 直交表的等效關係（Equivalence of Orthogonal Arrays） 7. 1 -2 純二水準直交表的建構：L 4(23)（Construction of a 2 -Level OA: L 4(23)） 7. 1 -3 其它純二水準直交表的建構（Construction of Other 2 -Level OA's） 7. 1 -4 純三水準直交表的建構（Construction of 3 -Level OA's） 7. 1 -5 混合水準直交表的建構（Construction of Mix-Level OA's） QE & DOE, Spring 2016, IUT, NSYSU

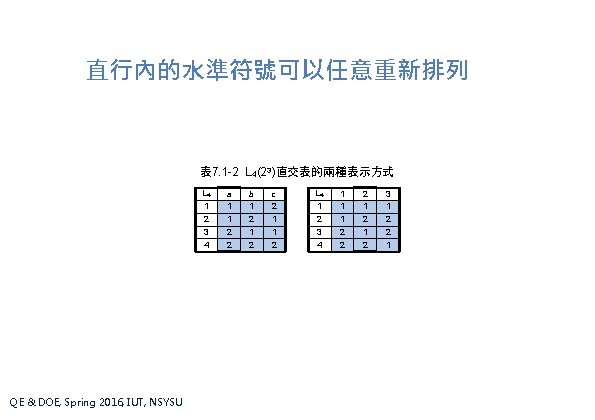
直行內的水準符號可以任意重新排列 表 7. 1 -2 L 4(23)直交表的兩種表示方式 L 4 1 2 3 4 QE & DOE, Spring 2016, IUT, NSYSU a 1 1 2 2 b 1 2 c 2 1 1 2 L 4 1 2 3 4 1 1 1 2 2 2 1 2 3 1 2 2 1

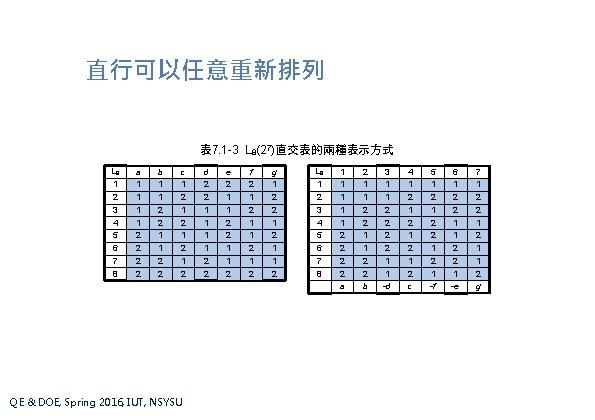
直行可以任意重新排列 表 7. 1 -3 L 8(27)直交表的兩種表示方式 L 8 1 2 3 4 5 6 7 8 a 1 1 2 2 b 1 1 2 2 c 1 2 1 2 QE & DOE, Spring 2016, IUT, NSYSU d 2 2 1 1 2 2 e 2 1 1 2 f 2 1 1 2 g 1 2 2 1 1 2 L 8 1 2 3 4 5 6 7 8 1 1 1 2 2 a 2 1 1 2 2 b 3 1 1 2 2 1 1 -d 4 1 2 1 2 c 5 1 2 2 1 -f 6 1 2 2 1 -e 7 1 2 2 1 1 2 g

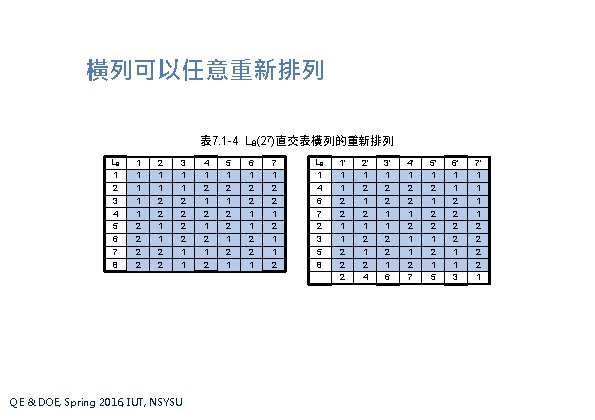
橫列可以任意重新排列 表 7. 1 -4 L 8(27)直交表橫列的重新排列 L 8 1 2 3 4 5 6 7 8 1 1 1 2 2 2 1 1 2 2 3 1 1 2 2 1 1 QE & DOE, Spring 2016, IUT, NSYSU 4 1 2 1 2 5 1 2 2 1 6 1 2 2 1 7 1 2 2 1 1 2 L 8 1 4 6 7 2 3 5 8 1' 1 1 2 2 2 2' 1 2 1 2 4 3' 1 2 2 1 6 4' 1 2 2 1 1 2 7 5' 1 2 2 1 5 6' 1 1 2 2 1 1 3 7' 1 1 2 2 1

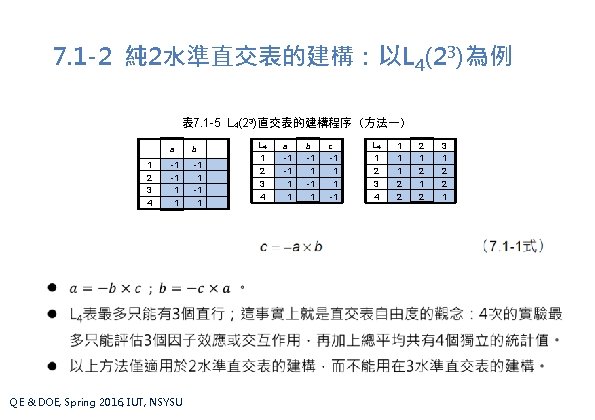
7. 1 -2 純 2水準直交表的建構：以L 4(23)為例 表 7. 1 -5 L 4(23)直交表的建構程序（方法一） 1 2 3 4 a b -1 -1 1 QE & DOE, Spring 2016, IUT, NSYSU L 4 1 2 3 4 a -1 -1 1 1 b -1 1 c -1 1 1 -1 L 4 1 2 3 4 1 1 1 2 2 2 1 2 3 1 2 2 1

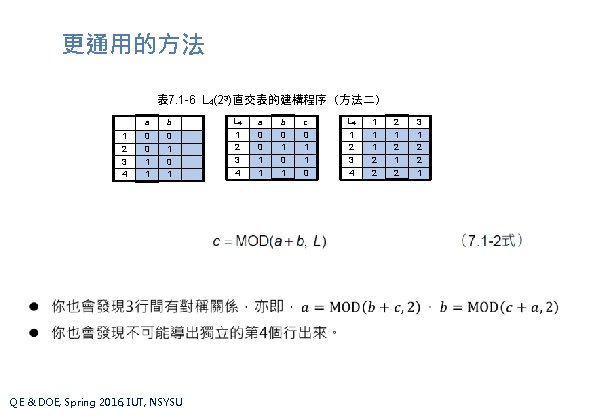
更通用的方法 表 7. 1 -6 L 4(23)直交表的建構程序（方法二） 1 2 3 4 a b 0 0 1 1 0 1 QE & DOE, Spring 2016, IUT, NSYSU L 4 1 2 3 4 a 0 0 1 1 b 0 1 c 0 1 1 0 L 4 1 2 3 4 1 1 1 2 2 2 1 2 3 1 2 2 1

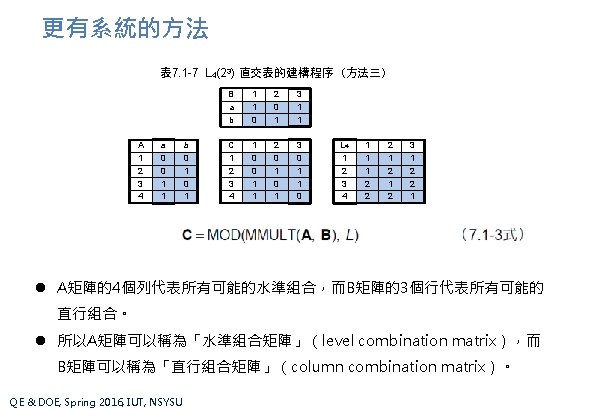
更有系統的方法 l 表 7. 1 -7的程序可以直接推廣至更大的純 2水準或純 3水準的直交表的建構。 l 這個程序甚至可以適用於純 5水準直交表的建構，但是純 4水準直交表的建 構程序需要做一些修改。因為 4水準及5水準直交表應用不多，所以本書不 予討論；若有需要，可以參考Ref. 26。 l Ref. 26: Kacker, R. N. , Lagergern, E. S. , and Filliben, J. J. , “Taguchi’s Orthogonal Arrays are Classical Designs of Experiments”, Vol. 96, No. 5, pp. 577 -591, Journal of Research of the National Institute of Standards and Technology , 1991. QE & DOE, Spring 2016, IUT, NSYSU

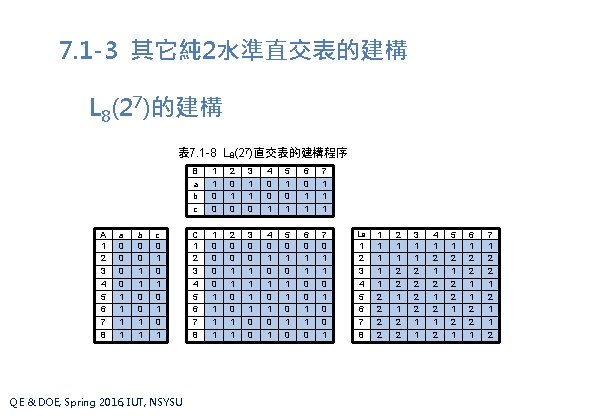
7. 1 -3 其它純 2水準直交表的建構 L 8(27)的建構 表 7. 1 -8 L 8(27)直交表的建構程序 A 1 2 3 4 5 6 7 8 a 0 0 1 1 b 0 0 1 1 c 0 1 0 1 QE & DOE, Spring 2016, IUT, NSYSU B a b c 1 1 0 0 2 0 1 0 3 1 1 0 4 0 0 1 5 1 0 1 6 0 1 1 7 1 1 1 C 1 2 3 4 5 6 7 8 1 0 0 1 1 2 0 0 1 1 3 0 0 1 1 0 0 4 0 1 0 1 5 0 1 1 0 6 0 1 1 0 7 0 1 1 0 0 1 L 8 1 2 3 4 5 6 7 8 1 1 1 2 2 2 1 1 2 2 3 1 1 2 2 1 1 4 1 2 1 2 5 1 2 2 1 6 1 2 2 1 7 1 2 2 1 1 2

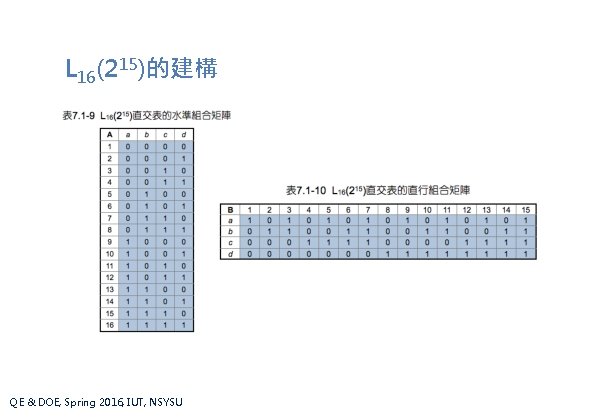
L 16(215)的建構 QE & DOE, Spring 2016, IUT, NSYSU

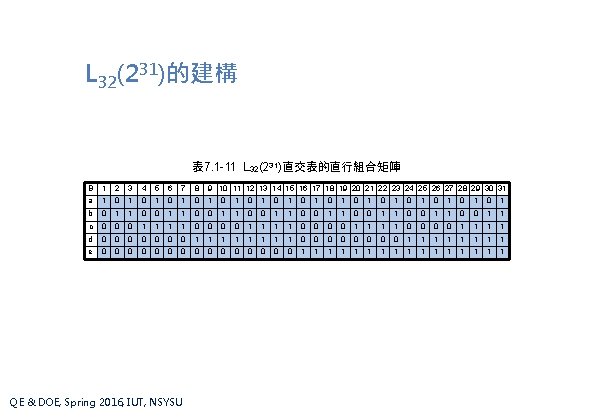
L 32(231)的建構 表 7. 1 -11 L 32(231)直交表的直行組合矩陣 B 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 a 1 0 1 0 1 0 1 0 1 b 0 1 1 0 0 1 1 0 0 1 1 c 0 0 0 1 1 1 1 0 0 0 0 1 1 d 0 0 0 0 1 1 1 1 e 0 0 0 0 1 1 1 1 QE & DOE, Spring 2016, IUT, NSYSU

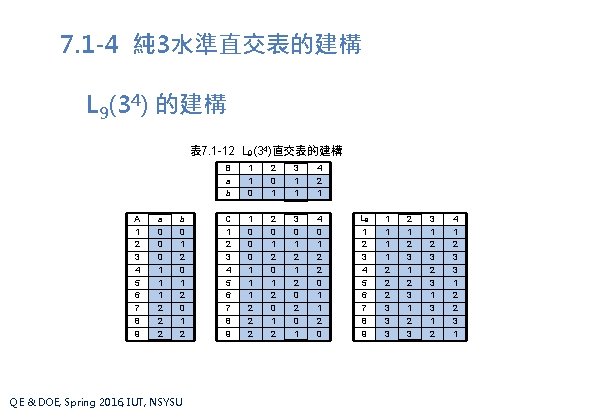
7. 1 -4 純 3水準直交表的建構 L 9(34) 的建構 表 7. 1 -12 L 9(34)直交表的建構 A 1 2 3 4 5 6 7 8 9 a 0 0 0 1 1 1 2 2 2 b 0 1 2 QE & DOE, Spring 2016, IUT, NSYSU B a b 1 1 0 2 0 1 3 1 1 4 2 1 C 1 2 3 4 5 6 7 8 9 1 0 0 0 1 1 1 2 2 0 1 2 3 0 1 2 0 2 0 1 4 0 1 2 2 0 1 1 2 0 L 9 1 2 3 4 5 6 7 8 9 1 1 2 2 2 3 3 3 2 1 2 3 3 1 2 3 1 3 1 2 4 1 2 3 3 1 2 2 3 1

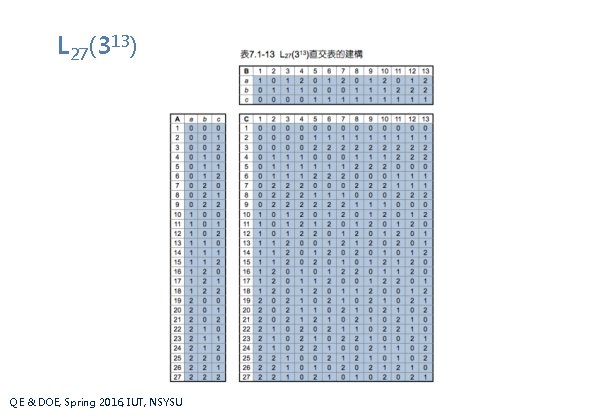
L 27(313) 的建構 QE & DOE, Spring 2016, IUT, NSYSU

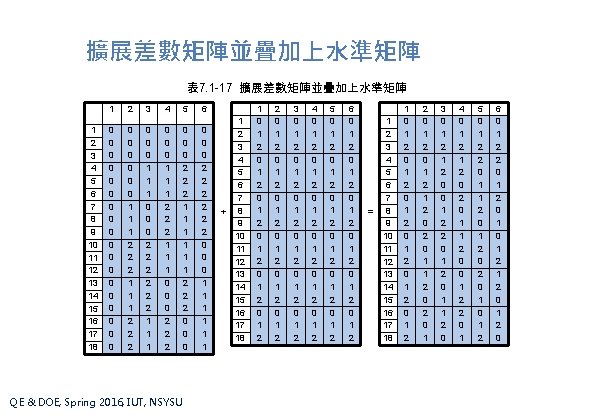
擴展差數矩陣並疊加上水準矩陣 表 7. 1 -17 擴展差數矩陣並疊加上水準矩陣 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 1 2 3 4 5 6 0 0 0 0 0 0 1 1 1 2 2 2 0 0 0 1 1 1 0 0 0 2 2 2 1 1 1 0 0 0 1 1 1 2 2 2 1 1 1 0 0 0 2 2 2 1 1 1 2 2 2 0 0 0 1 1 1 QE & DOE, Spring 2016, IUT, NSYSU + 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 1 0 1 2 0 1 2 2 0 1 2 0 1 2 3 0 1 2 0 1 2 4 0 1 2 0 1 2 5 0 1 2 0 1 2 6 0 1 2 0 1 2 = 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 1 0 1 2 0 1 2 2 0 1 2 1 2 0 2 0 1 3 0 1 2 0 0 1 2 2 0 1 1 2 0 4 0 1 2 0 2 0 1 1 2 0 0 1 2 2 0 1 5 0 1 2 2 0 1 1 2 0 2 0 1 2 6 0 1 2 2 0 1 0 1 2 0

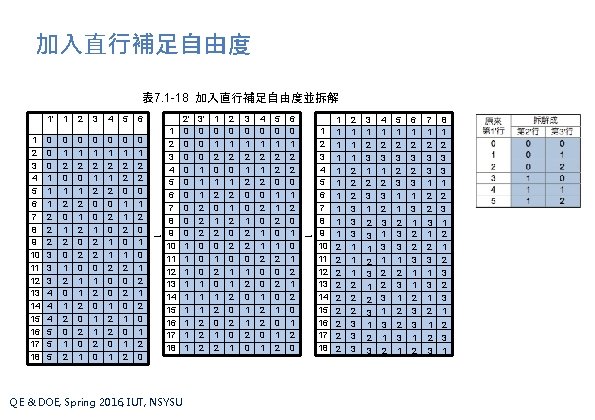
加入直行補足自由度 表 7. 1 -18 加入直行補足自由度並拆解 1' 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 0 0 0 1 1 1 2 2 2 3 3 3 4 4 4 5 5 5 1 0 1 2 0 1 2 2 0 1 2 1 2 0 2 0 1 3 0 1 2 0 0 1 2 2 0 1 1 2 0 4 0 1 2 0 2 0 1 1 2 0 0 1 2 2 0 1 5 0 1 2 2 0 1 1 2 0 2 0 1 2 6 0 1 2 2 0 1 0 1 2 3 4 5 6 7 8 → 9 10 11 12 13 14 15 16 17 18 QE & DOE, Spring 2016, IUT, NSYSU 2' 3' 0 0 0 0 1 0 1 0 2 0 2 1 0 1 0 1 1 1 1 2 1 2 1 0 1 2 0 1 2 2 0 1 2 1 2 0 2 0 1 3 0 1 2 0 0 1 2 2 0 1 1 2 0 4 0 1 2 0 2 0 1 1 2 0 0 1 2 2 0 1 5 0 1 2 2 0 1 1 2 0 2 0 1 2 6 0 1 2 2 0 1 0 1 2 3 4 5 6 7 8 → 9 10 11 12 13 14 15 16 17 18 1 1 1 1 1 2 2 2 2 2 1 1 1 2 2 2 3 3 3 3 1 2 3 1 4 1 2 3 2 5 1 2 3 1 1 6 1 2 3 1 3 7 1 2 3 3 1 2 2 8 1 2 3 3 1 2 3 1 2 3 3 1 2 2 3 1 2 2 3 1 1 2 3 3 1 2 1 2 3 1 3 1 2 2 3 1 2 1 2 3 1

L 36(23 x 313)的建構 QE & DOE, Spring 2016, IUT, NSYSU