MATH 685 CSI 700 OR 682 Lecture Notes

Eigenvalue problems l Eigenvalue problems occur in many areas of science and engineering, such

Formulation Matrix expands or shrinks any vector lying in direction of eigenvector by scalar

Characteristic polynomial l Computing eigenvalues using characteristic polynomial is not recommended because of l

Properties of eigenvalue problems l Properties of eigenvalue problem affecting choice of algorithm and

Diagonal form l Eigenvalues of diagonal matrix are diagonal entries, and eigenvectors are columns

Power Iteration with Shift In earlier example, for instance, if we pick shift of

Inverse iteration converges to eigenvector corresponding to smallest eigenvalue of A. Eigenvalue obtained is

Process continues until off-diagonal entries reduced to as small as desired Result is diagonal

Slides: 78

Download presentation

MATH 685/ CSI 700/ OR 682 Lecture Notes Lecture 6. Eigenvalue problems.

Eigenvalue problems l Eigenvalue problems occur in many areas of science and engineering, such as structural analysis l Eigenvalues are also important in analyzing numerical methods l Theory and algorithms apply to complex matrices as well as real matrices l With complex matrices, we use conjugate transpose, AH, instead of usual transpose, AT

Formulation Matrix expands or shrinks any vector lying in direction of eigenvector by scalar factor Expansion or contraction factor is given by corresponding eigenvalue Eigenvalues and eigenvectors decompose complicated behavior of general linear transformation into simpler actions

Examples

Characteristic polynomial

Example

Companion matrix

Characteristic polynomial l Computing eigenvalues using characteristic polynomial is not recommended because of l l work in computing coefficients of characteristic polynomial sensitivity of coefficients of characteristic polynomial work in solving for roots of characteristic polynomial Characteristic polynomial is powerful theoretical tool but usually not useful computationally

Example

Diagonalizability

Eigenspaces

Some relevant definitions

Examples

Properties of eigenvalue problems l Properties of eigenvalue problem affecting choice of algorithm and software l l l l Are all eigenvalues needed, or only a few? Are only eigenvalues needed, or are corresponding eigenvectors also needed? Is matrix real or complex? Is matrix relatively small and dense, or large and sparse? Does matrix have any special properties, such as symmetry, or is it general matrix? Condition of eigenvalue problem is sensitivity of eigenvalues and eigenvectors to changes in matrix Conditioning of eigenvalue problem is not same as conditioning of solution to linear system for same matrix Different eigenvalues and eigenvectors are not necessarily equally sensitive to perturbations in matrix

Conditioning of eigenvalues

Problem transformations

Similarity transformation

Diagonal form l Eigenvalues of diagonal matrix are diagonal entries, and eigenvectors are columns of identity matrix l Diagonal form is desirable in simplifying eigenvalue problems for general matrices by similarity transformations l But not all matrices are diagonalizable by similarity transformation l Closest one can get, in general, is Jordan form, which is nearly diagonal but may have some nonzero entries on first superdiagonal, corresponding to one or more multiple eigenvalues

Triangular form

Block triangular form

Forms attainable by similarity

Power iteration

Convergence of Power iteration

Example

Limitations

Normalized Power iteration

Example

Geometric interpretation

Power Iteration with Shift In earlier example, for instance, if we pick shift of σ = 1, (which is equal to other eigenvalue) then ratio becomes zero and method converges in one iteration In general, we would not be able to make such fortuitous choice, but shifts can still be extremely useful in some contexts, as we will see later

Inverse iteration converges to eigenvector corresponding to smallest eigenvalue of A. Eigenvalue obtained is dominant eigenvalue of A− 1, and hence its reciprocal is smallest eigenvalue of A in modulus

Example

Shifted inverse iteration

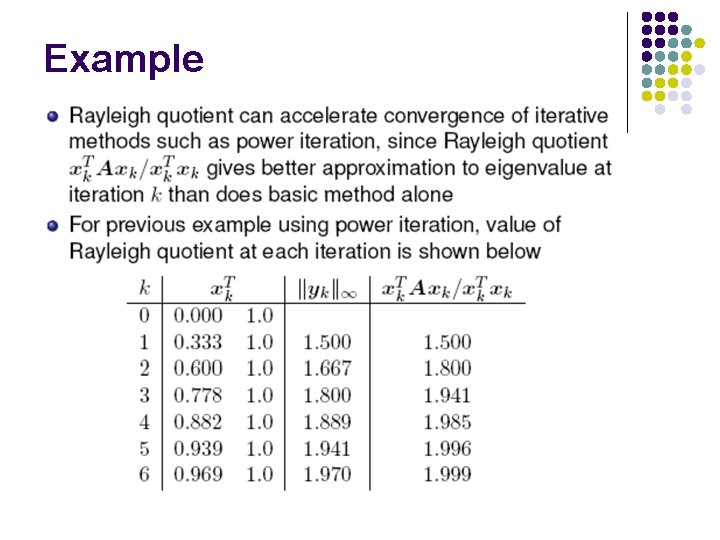
Rayleigh Quotient

Example

Rayleigh Quotient iteration

Deflation

Simultaneous Iteration

Orthogonal iteration

QR iteration

Example

QR iteration with shifts

Example

Preliminary reduction

Cost of QR iteration

Krylov subspaces methods

Arnoldi iteration

Lanczos Iteration

Lanczos iteration

Krylov subspace methods cont.

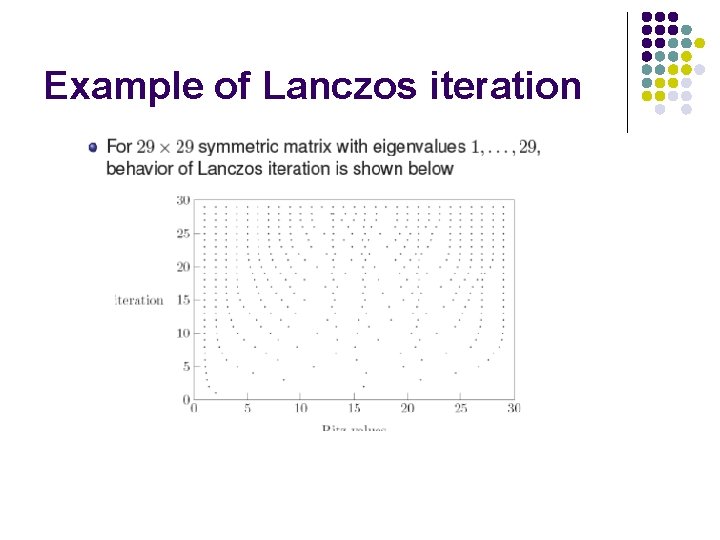
Example of Lanczos iteration

Jacobi method

Plane rotation

Jacobi method cont.

Jacobi method example

Process continues until off-diagonal entries reduced to as small as desired Result is diagonal matrix orthogonally similar to original matrix, with the orthogonal similarity transformation given by product of plane rotations

Other methods (spectrum-slicing)

Sturm sequence

Divide-and-conquer algorithm

Relatively robust representation

Generalized eigenvalue problems

QZ algorithm

Computing SVD