Fundamentals of Computer Graphics Part 5 Viewing prof

Fundamentals of Computer Graphics Part 5 Viewing prof. ing. Václav Skala, CSc. University of West Bohemia Plzeň, Czech Republic © 2002 Prepared with Angel, E. : Interactive Computer Graphics – A Top Down Approach with Open. GL, Addison Wesley, 2001 Fundamentals of Computer Graphics

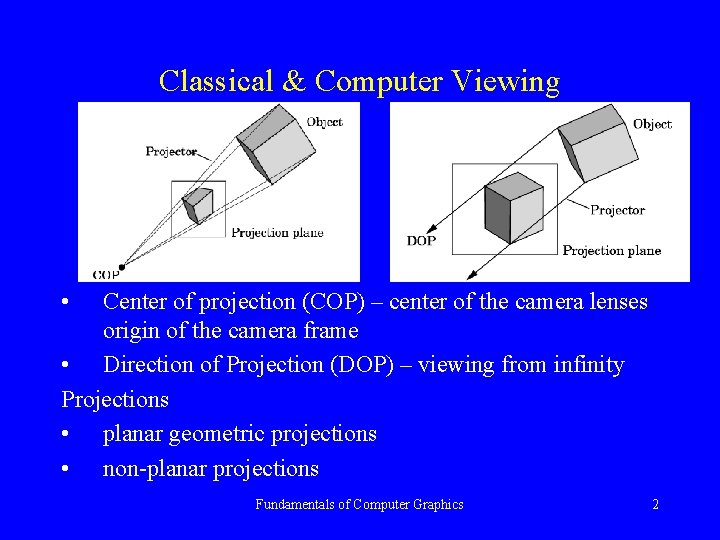
Classical & Computer Viewing • Center of projection (COP) – center of the camera lenses origin of the camera frame • Direction of Projection (DOP) – viewing from infinity Projections • planar geometric projections • non-planar projections Fundamentals of Computer Graphics 2

Classical Views • • principal faces; architectural building-mostly orthogonal faces front, back, top, bottom, right, left faces Fundamentals of Computer Graphics 3

Orthographic Projections Multi-view orthographic projection (rovnoběžné promítání) • 3 views & orthogonal • preserves angles Fundamentals of Computer Graphics 4

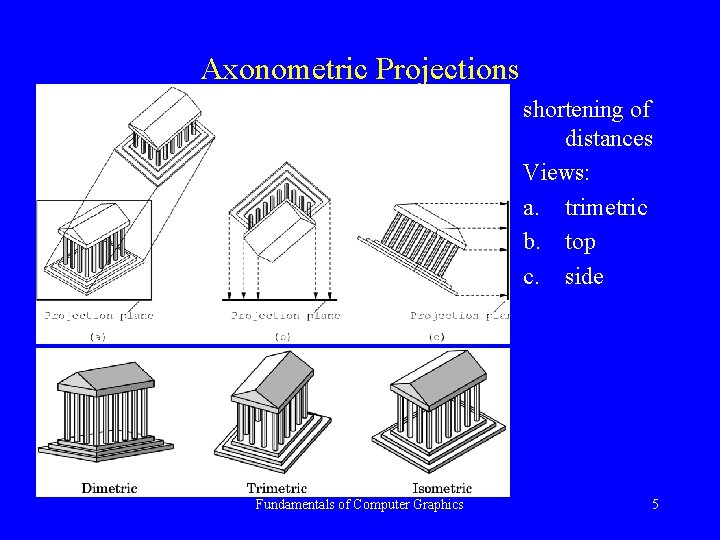
Axonometric Projections shortening of distances Views: a. trimetric b. top c. side Fundamentals of Computer Graphics 5

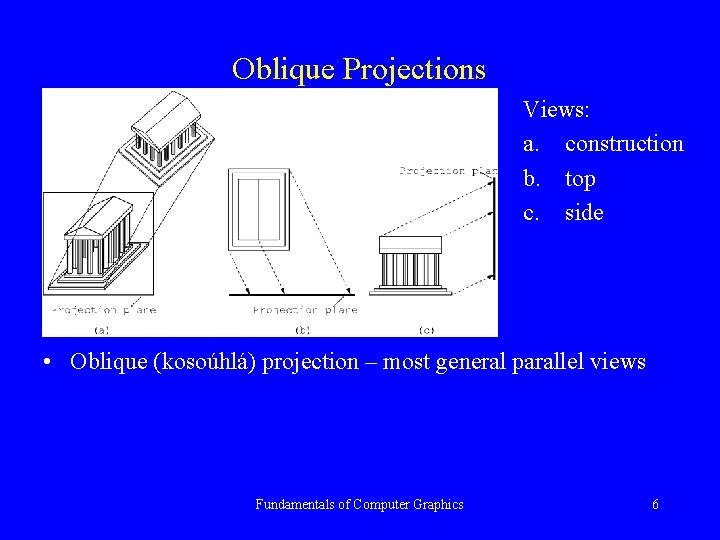
Oblique Projections Views: a. construction b. top c. side • Oblique (kosoúhlá) projection – most general parallel views Fundamentals of Computer Graphics 6

Perspective Projections Vanishing point(s) (úběžník) • one-point • two-points • three-points perspectives Fundamentals of Computer Graphics 7

Camera positioning Vanishing point(s) (úběžník) • one-point • two-points • three-points perspectives ! right-handed x left-handed coordinates gl. Ortho(. . , near, far) measured from the camera gl. Translate (0. 0, -d); /* moves the camera in positive dir. of z Fundamentals of Computer Graphics 8

Camera positioning We want to see objects from distance d and from x axis direction: gl. Matrix. Mode(GL_MODEL_VIEW); gl. Load. Identity ( ); gl. Translate (0. 0, -d); gl. Rotate(-90. 0, 1. 0, 0. 0); Order: 1. rotate 2. move away from the origin Fundamentals of Computer Graphics 9

Camera positioning Isometric view of a cube [-1, -1] x [1, 1, 1] Order: 1. rotate about y-axis 2. rotate about x-axis 3. move away from the origin gl. Matrix. Mode(GL_MODELVIEW); corner [-1, 1, 1] to be gl. Load. Identity (); transformed to [0, 1, 2] 35. 26° gl. Translatef(0. 0, -d); /* 3 -rd */ gl. Rotatef(35. 26, 1. 0, 0. 0); /* 2 -nd */ gl. Rotatef(45. 0, 0. 0, 1. 0, 0. 0); /* 1 -st */ Fundamentals of Computer Graphics 10

Two viewing API’s Unsatisfactory camera specification Starting point – world frame – description of camera position and orientation; precise type of image – perspective or parallel defined separately – Projection Matrix specification VRP – View Reference Point – origin is implicit set_view_reference_point(x, y, z); VPN – View Plane Normal – orientation of projection plane – camera back set_view_plane_normal(nx, ny, nz); VUP – View-UP vector - specifies what direction is up from the camera’s perspective set_view_up(vup_x, vup_y, vup_z); Fundamentals of Computer Graphics 11

Two viewing API’s v vector is obtained by VUP vector projection on the view plane; v is orthogonal to normal n This orthogonal system is referred as • viewing-coordinate system or • u-v-n system with VRP added - desired camera frame The matrix that DOES the change of frames is the view-orientation matrix p = [x, y, z, 1]T – view-reference point n = [nx, ny, nz, 0]T – view-plane normal vup = [vupx, vupy, vupz, 0]T – view-up vector Fundamentals of Computer Graphics 12

Two viewing API’s New frame construction • view-reference point as its origin • view-plane normal as one coordinate direction • two other directions u & v Default x, y, z axes become u, v, n now Model-view matrix V = T R ; v & n must be orthogonal n. Tv = 0 v is a projection of vup into the plane formed by n & vup – it must be a linear combination of these two vectors v = n + vup If the length of v is ignored, = 1 can be set and = - p. Tn / n. Tn v = p – ( p. Tn / n. Tn ) n u=vxn Fundamentals of Computer Graphics 13

Two viewing API’s Vectors u, v, n can be normalized independently to u’, v’, n’ Matrix M is a rotation matrix that orients u’, v’, n’ system with respect to the original system We want inversion matrix R R = M-1 = MT Finally the model-view matrix V=TR For our isometric example p = ( 3/3) [-d, d, d, 1]T n = [-1, 1, 1, 0]T vup = [0, 1, 0, 0]T Fundamentals of Computer Graphics 14

Look-At Function VRP, VPN & VUP specifies camera position Straightforward method: e – camera position (called eye-point) a – position to look at (called at point) vpn = e – a glu. Look. At(eye_x, eye_y, eye_z, at_x, at_y, at_z ) ; Fundamentals of Computer Graphics 15

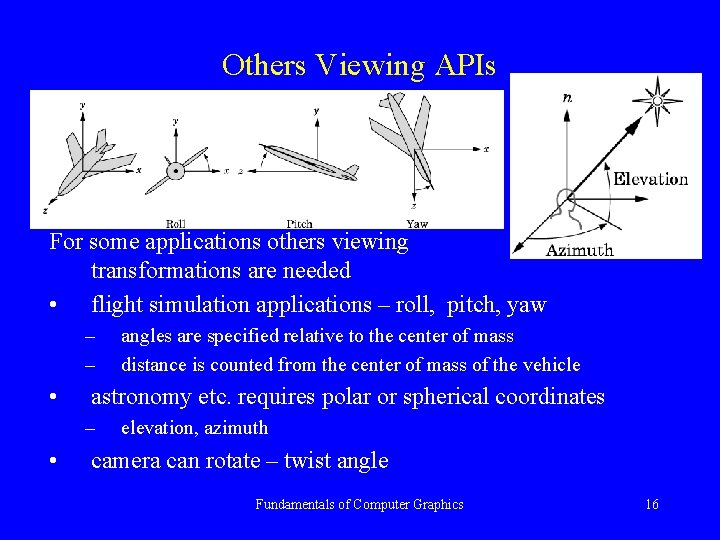
Others Viewing APIs For some applications others viewing transformations are needed • flight simulation applications – roll, pitch, yaw – – • astronomy etc. requires polar or spherical coordinates – • angles are specified relative to the center of mass distance is counted from the center of mass of the vehicle elevation, azimuth camera can rotate – twist angle Fundamentals of Computer Graphics 16

Perspective Projections Camera is pointing in the negative z-direction , d < 0 x / z = xp / d xp = x / (z /d) yp = y / (z /d) division by z describes non-uniform foreshortening Perspective transformation preserves lines, but • it is not affine • it is irreversible Fundamentals of Computer Graphics 17

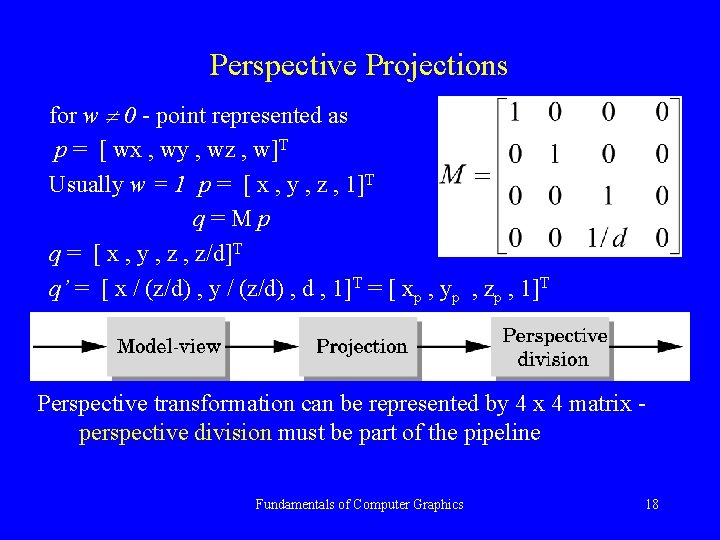
Perspective Projections for w 0 - point represented as p = [ wx , wy , wz , w]T Usually w = 1 p = [ x , y , z , 1]T q=Mp q = [ x , y , z/d]T q’ = [ x / (z/d) , y / (z/d) , d , 1]T = [ xp , yp , zp , 1]T Perspective transformation can be represented by 4 x 4 matrix perspective division must be part of the pipeline Fundamentals of Computer Graphics 18

Orthogonal Projections Orthogonal or orthographic projection is a special case After projection: xp = x yp = y zp = 0 Fundamentals of Computer Graphics 19

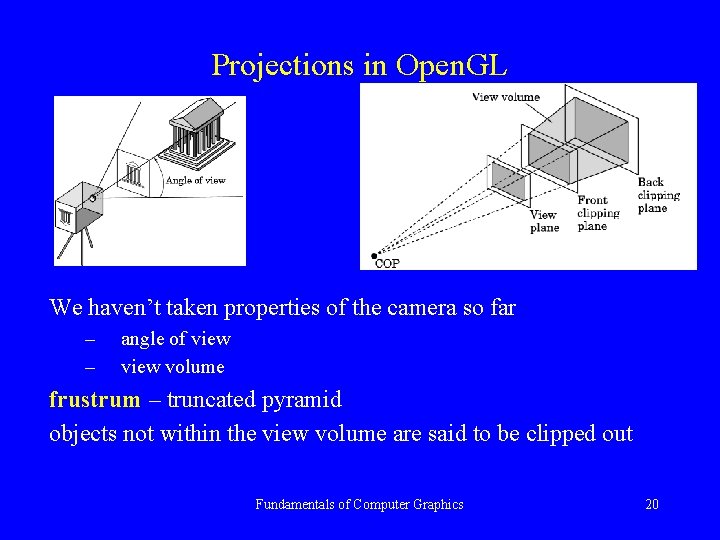
Projections in Open. GL We haven’t taken properties of the camera so far – – angle of view volume frustrum – truncated pyramid objects not within the view volume are said to be clipped out Fundamentals of Computer Graphics 20

Perspective viewing in Open. GL Typical sequence: gl. Matrix. Mode (GL_PROJECTION); gl. Load. Identity ( ); gl. Frustrum(xmin, xmax, ymin, ymax, near, far); near & far distances must be positive and measured from the COP be careful about the signs ! Fundamentals of Computer Graphics 21

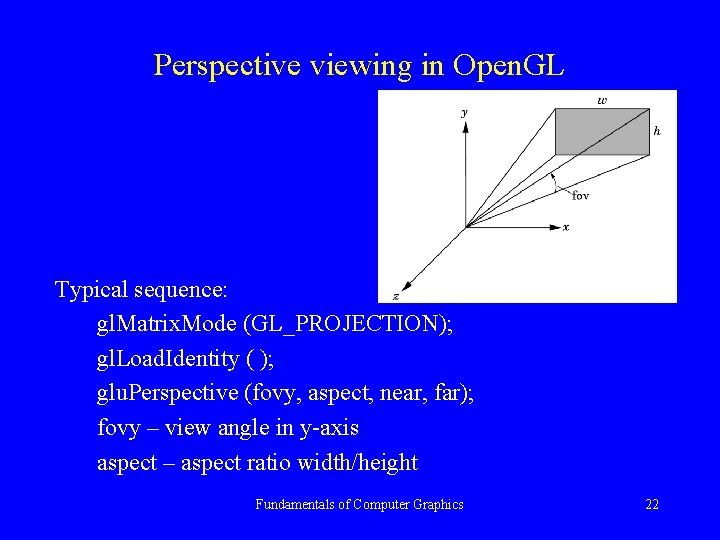
Perspective viewing in Open. GL Typical sequence: gl. Matrix. Mode (GL_PROJECTION); gl. Load. Identity ( ); glu. Perspective (fovy, aspect, near, far); fovy – view angle in y-axis aspect – aspect ratio width/height Fundamentals of Computer Graphics 22

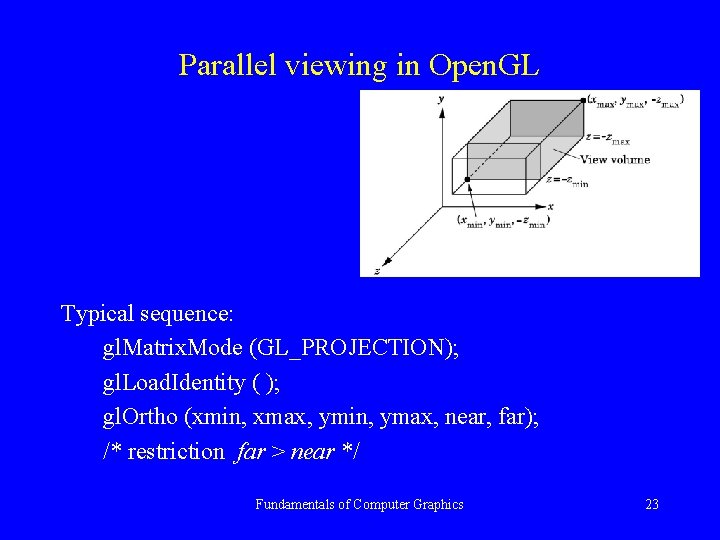
Parallel viewing in Open. GL Typical sequence: gl. Matrix. Mode (GL_PROJECTION); gl. Load. Identity ( ); gl. Ortho (xmin, xmax, ymin, ymax, near, far); /* restriction far > near */ Fundamentals of Computer Graphics 23

Hidden Surface Removal Algorithms • object space • image space – z-buffer – requires depth or z-buffer Typical sequence: glut. Init. Display. Mode (GLUT_DOUBLE | GLUT_RGB | GLUT_DEPTH); gl. Enable(GL_DEPTH_TEST); Clear the buffer before new rendering gl. Clear(GL_DEPTH_BUFFER_BIT); /* study example in chapter 5. 6 */ Fundamentals of Computer Graphics 24

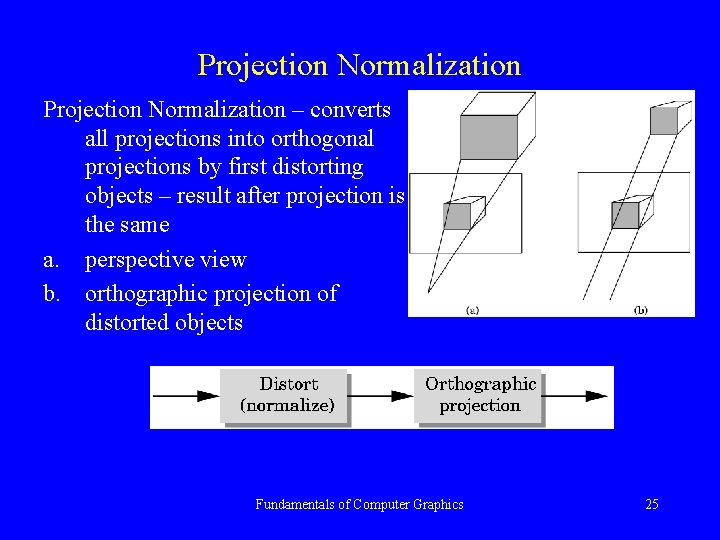
Projection Normalization – converts all projections into orthogonal projections by first distorting objects – result after projection is the same a. perspective view b. orthographic projection of distorted objects Fundamentals of Computer Graphics 25

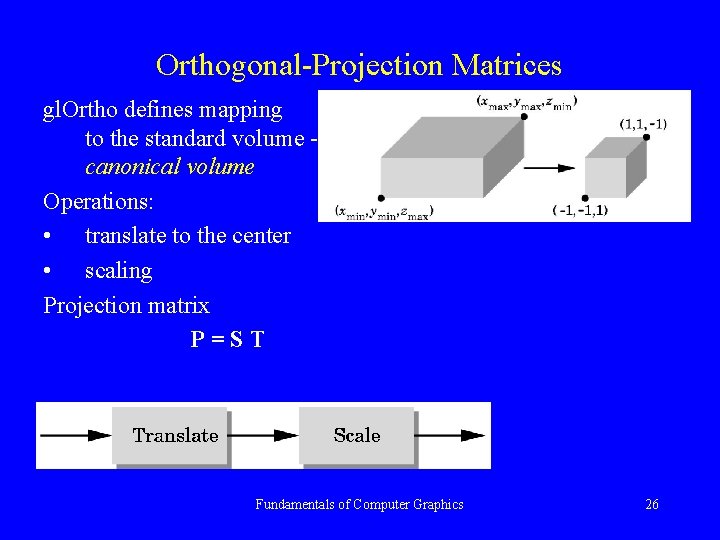
Orthogonal-Projection Matrices gl. Ortho defines mapping to the standard volume canonical volume Operations: • translate to the center • scaling Projection matrix P=ST Fundamentals of Computer Graphics 26

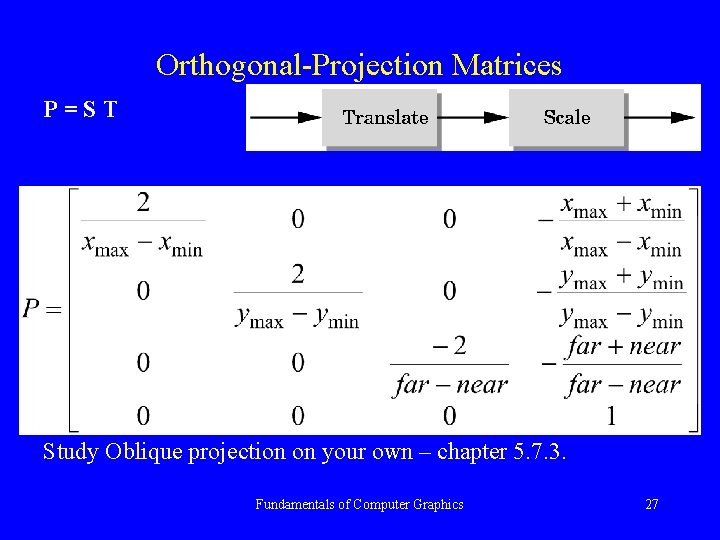
Orthogonal-Projection Matrices P=ST Study Oblique projection on your own – chapter 5. 7. 3. Fundamentals of Computer Graphics 27

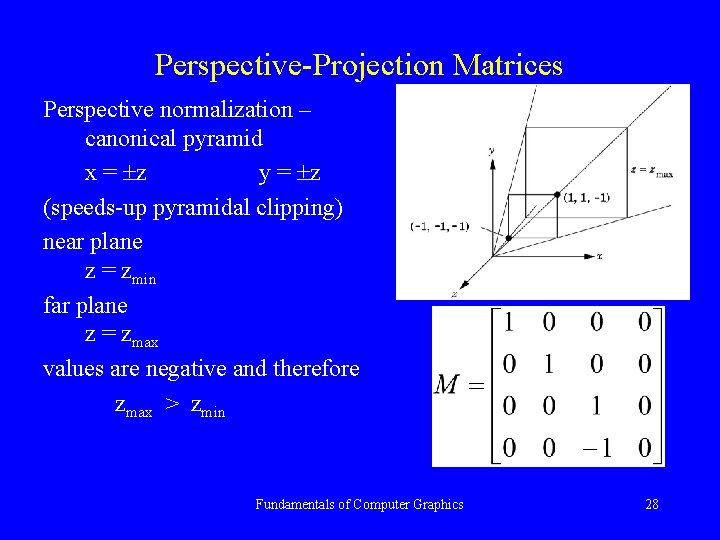
Perspective-Projection Matrices Perspective normalization – canonical pyramid x = z y = z (speeds-up pyramidal clipping) near plane z = zmin far plane z = zmax values are negative and therefore zmax > zmin Fundamentals of Computer Graphics 28

Perspective-Projection Matrices Consider a matrix N p = [ x, y, z, 1]T q = [ x’, y’, z’, w’]T q=Np x’ = x y’ = y z’ = z + w’ = -z after dividing x’’ = - x /d y’’ = -y /d z’’ = -( + / z) w’’= 1 if orthographic projection is applied along to z axis p’ = Morth. N p = [ x, y, 0, -z ]T Fundamentals of Computer Graphics 29

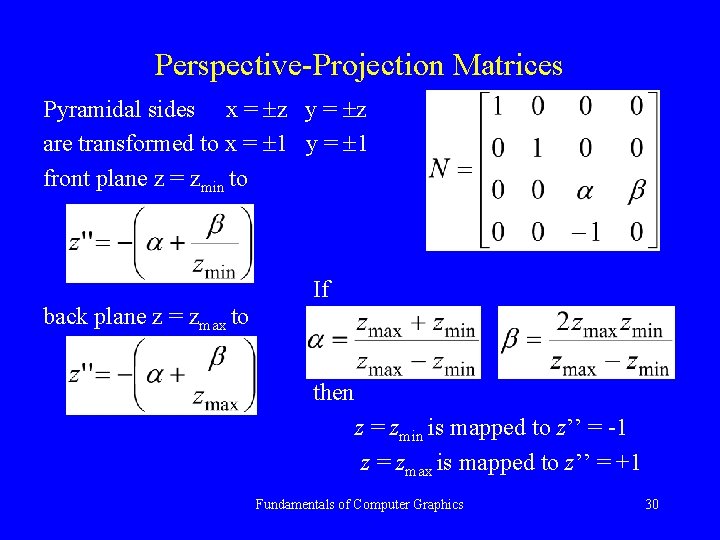
Perspective-Projection Matrices Pyramidal sides x = z y = z are transformed to x = 1 y = 1 front plane z = zmin to If back plane z = zmax to then z = zmin is mapped to z’’ = -1 z = zmax is mapped to z’’ = +1 Fundamentals of Computer Graphics 30

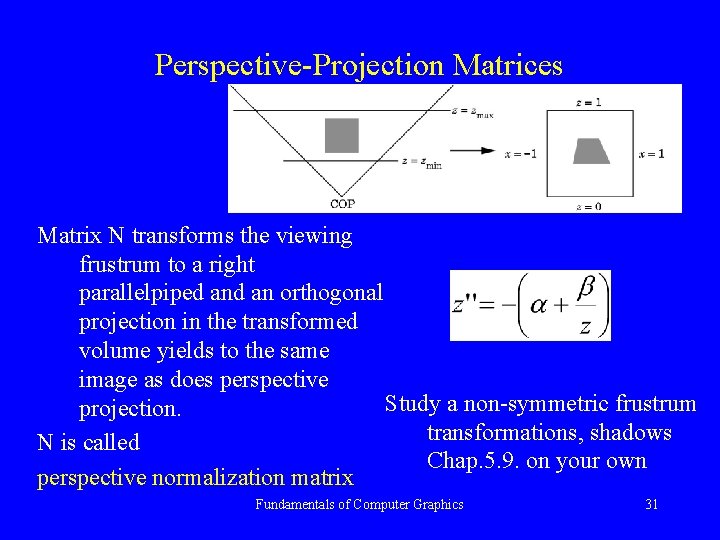
Perspective-Projection Matrices Matrix N transforms the viewing frustrum to a right parallelpiped an orthogonal projection in the transformed volume yields to the same image as does perspective Study a non-symmetric frustrum projection. transformations, shadows N is called Chap. 5. 9. on your own perspective normalization matrix Fundamentals of Computer Graphics 31

Conclusion - Chapter 5 You have learnt mathematical background and API for projections – parallel, oblique and perspective Try to find a solution for: 1. define transformations needed for flight simulator as a composition of existing ones 2. application of projections for a display walls (4 x 3 screens, using non-symmetric viewing frustrum) 3. imagine a cube in perspective projection. Observer is – in front of the object – inside of the object what he will see, what you will get if you use geometric transformations and projection matrices and what Open. GL gives you? Discuss results! Fundamentals of Computer Graphics 32