Computer graphics III Rendering equation and its solution












































![Path tracing [Kajiya 86] n Only one secondary ray at each intersection q n Path tracing [Kajiya 86] n Only one secondary ray at each intersection q n](https://slidetodoc.com/presentation_image_h/7309dd970a8a35badcfd818debd0b9b8/image-46.jpg)
- Slides: 46

Computer graphics III – Rendering equation and its solution Jaroslav Křivánek, MFF UK Jaroslav. Krivanek@mff. cuni. cz

Global illumination – GI Direct illumination Global = direct + indirect 2

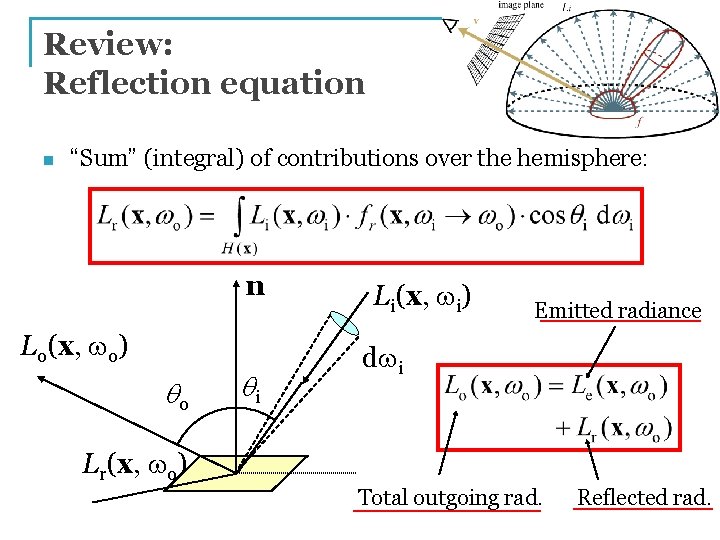
Review: Reflection equation n “Sum” (integral) of contributions over the hemisphere: n Lo(x, wo) qo qi Li(x, wi) Emitted radiance dwi Lr(x, wo) Total outgoing rad. Reflected rad.

From local reflection to global light transport n Reflection equation (local reflection) n Where does the incoming radiance Li(x, wi) come from? q From other places in the scene ! Lo( r(x, wi), -wi) = Li(x, wi) Ray casting function CG III (NPGR 010) - J. Křivánek 2015 x r(x, wi)

From local reflection to global light transport n Plug for Li into the reflection equation n Incoming radiance Li drops out Outgoing radiance Lo at x described in terms of Lo at other points in the scene n CG III (NPGR 010) - J. Křivánek 2015

Rendering equation n Remove the subscript “o” from the outgoing radiance: n Description of the steady state = energy balance in the scene Rendering = calculate L(x, wo) for all points visible through pixels, such that it fulfils the rendering equation n CG III (NPGR 010) - J. Křivánek 2015

Reflection equation vs. Rendering equation Similar form – different meaning n Reflection equation q q Describes local light reflection at a single point Integral that can be used to calculate the outgoing radiance if we know the incoming radiance n Rendering equation q q Condition on the global distribution of light in scene Integral equation – unknown quantity L on both sides

Rendering Equation – Kajiya 1986 CG III (NPGR 010) - J. Křivánek 2015

Path tracing sketch

Recursive unwinding of the RE n n Angular form of the RE To calculate L(x, wo), we need to calculate L(r(x, w’), -w’) for all directions w’ around the point x For the calculation of each L(r(x, w’), -w’), we need to do the same thing recursively, etc. r( r(x, w’) w’’ w’ wo x CG III (NPGR 010) - J. Křivánek 2015 r(x, w’)

Path tracing, v. zero (recursive form) get. Li (x, ω): y = trace. Ray(x, ω) return Le(y, –ω) + Lr (y, –ω) // emitted radiance // reflected radiance Lr(x, ω): ω′ = gen. Uniform. Hemisphere. Random. Dir( n(x) ) return 2 p * brdf(x, ω, ω′) * dot(n(x), ω′) * get. Li(x, ω′) CG III (NPGR 010) - J. Křivánek 2015

Back to theory: Angular and area form of the rendering equation

Angular vs. area form of the RE n Angular form q n integral over the hemisphere in incoming directions Substitution CG III (NPGR 010) - J. Křivánek 2015

Angular vs. area form of the RE n Area form q Integral over the scene surface geometry term CG III (NPGR 010) - J. Křivánek 2015 visibility 1 … y visible from x 0 … otherwise

Angular form n Add radiance contributions to a point from all directions n For each direction, find the nearest surface n Implementation in stochastic path tracing: q For a given x, generate random direction(s), for each find the nearest intersection, return the outgoing radiance at that intersection and multiply it with the cosine-weighted BRDF. Average the result of this calculation over all the generated directions over the hemisphere. CG III (NPGR 010) - J. Křivánek 2015

Area form n Sum up contributions to a point from all other points on the scene surface n Contribution added only if the two points are mutually visible n Implementation in stochastic path tracing: q n Generate randomly point y on scene geometry. Test visibility between x and y. If mutually visible, add the outgoing radiance at y modulated by the geometry factor. Typical use: direct illumination calculation for area light sources CG III (NPGR 010) - J. Křivánek 2015

Most rendering algorithms = (approximate) solution of the RE n Local illumination (Open. GL) q q n Only point sources, integral becomes a sum Does not calculate equilibrium radiance, is not really a solution of the RE Finite element methods (radiosity) [Goral, ’ 84] q q q Discretize scene surface (finite elements) Disregard directionality of reflections: everything is assumed to be diffuse Cannot reproduce glossy reflections CG III (NPGR 010) - J. Křivánek 2015

Most rendering algorithms = (approximate) solution of the RE n Ray tracing [Whitted, ’ 80] q q q n Direct illumination on diffuse and glossy surfaces due to point sources Indirect illumination only on ideal mirror reflection / refractions Cannot calculate indirect illumination on diffuse and glossy scenes, soft shadows etc. … Distributed ray tracing [Cook, ’ 84] q q Estimate the local reflection using the MC method Can calculate soft shadows, glossy reflections, camera defocus blur, etc. CG III (NPGR 010) - J. Křivánek 2015

Most rendering algorithms = (approximate) solution of the RE n Path tracing [Kajiya, ’ 86] q q q True solution of the RE via the Monte Carlo method Tracing of random paths (random walks) from the camera Can calculate indirect illumination of higher order CG III (NPGR 010) - J. Křivánek 2015

From the rendering equation to finite element radiosity

From the rendering equation to radiosity n Start from the area form of the RE: n The Radiosity method– assumptions q q Only diffuse surfaces (BRDF constant in wi and wo) Radiosity (i. e. radiant exitance) is spatially constant (flat) over the individual elements CG III (NPGR 010) - J. Křivánek 2015

From the rendering equation to radiosity n Diffuse surfaces only q q The BRDF is constant in wi and wo Outgoing radiance is independent of wo and it is equal to radiosity B divided by p CG III (NPGR 010) - J. Křivánek 2015

From the rendering equation to radiosity n Spatially constant (flat) radiosity B of the contributing surface elements Radiosity of the j-th element Geometry factor between surface element j and point x CG III (NPGR 010) - J. Křivánek 2015

From the rendering equation to radiosity n Spatially constant (flat) radiosity of the receiving surface element i: q Average radiosity over the element … form factor CG III (NPGR 010) - J. Křivánek 2015

Classic radiosity equation n System of linear equations n Form factors n Conclusion: the radiosity method is nothing but a way to solve the RE under a specific set of assumptions CG III (NPGR 010) - J. Křivánek 2015

Radiosity method n Classical radiosity 1. 2. n Stochastic radiosity q q n Form facto calculation (Monte Carlo, hemicube, …) Solve the linear system (Gathering, Shooting, …) Avoids explicit calculation of form factors Metoda Monte Carlo Radiosity is not practical, not used q q Scene subdivision -> sensitive to the quality of the geometry model (but in reality, models are always broken) High memory consumption, complex implementation CG III (NPGR 010) - J. Křivánek 2015

The operator form of the RE

RE is a Fredhom integral equation of the 2 nd kind General form the Fredholm integral equation of the 2 nd kind unknown functions Rendering equation: CG III (NPGR 010) - J. Křivánek 2015 equation “kernel”

Linear operators FIX NOTATION n (L shoul Linear operators act on functions q (as matrices act on vectors) n The operator is linear if the “acting” is a linear operation n Examples of linear operators CG III (NPGR 010) - J. Křivánek 2015

Transport operator n Rendering equation CG III (NPGR 010) - J. Křivánek 2015

Solution of the RE in the operator form n Rendering equation n Formal solution n unusable in practice – the inverse cannot be explicitly calculated CG III (NPGR 010) - J. Křivánek 2015

Expansion of the rendering equation n Recursive substitution L n n-fold repetition yields the Neumann series CG III (NPGR 010) - J. Křivánek 2015

Expansion of the rendering equation n If T is a contraction (tj. ||T|| < 1, which holds for the RE), then n Solution of the rendering equation is then given by CG III (NPGR 010) - J. Křivánek 2015

A different derivation of the Neumann series n Formal solution of the rendering equation n Proposition n Proof CG III (NPGR 010) - J. Křivánek 2015

Rendering equation n Solution: Neumann series CG III (NPGR 010) - J. Křivánek 2015

Progressive approximation CG III (NPGR 010) - J. Křivánek 2015

Progressive approximation n Each application of T corresponds to one step of reflection & light propagation one-bounce indirect illumination emission direct illumination Open. GL shading CG III (NPGR 010) - J. Křivánek 2015 two-bounce indirect illumination

Contractivity of T n Holds for all physically correct models q Follows from the conservation of energy n It means that repetitive application of the operator lower the remaining light energy (makes sense, since reflection/refraction cannot create energy) n Scenes with white or highly specular surfaces q q reflectivity close to 1 to achieve convergence, we need to simulate more bounces of light CG III (NPGR 010) - J. Křivánek 2015

Alright, so what have we achieved? Rendering equation n Solution through the Neumann series We have replaced an integral equation by a sum of simple integrals Great we know how to calculate integrals numerically (the Monte Carlo method), which means that we know how to solve the RE, and that means that we can render images, yay! Recursive application to T corresponds to the recursive ray tracing from the camera CG III (NPGR 010) - J. Křivánek 2015

What exact integral are we evaluating, then? CG III (NPGR 010) - J. Křivánek 2015

Paths vs. recursion: Same thing, depends on how we look at it n Paths in a high-dimensional path space n Recursive solution of a series of nested (hemi)spherical integrals: CG III (NPGR 010) - J. Křivánek 2015

Recursive interpretation n n We’ve seen this already, right? But unlike at the beginning of the lecture, by now we know this actually solves the RE. Angular form of the RE To calculate L(x, wo) I need to calculate L(r(x, w’), -w’) for all directions w’ around the point x. For the calculation of each L(r(x, w’), -w’) I need to do the same thing recursively etc. r( r(x, w’) w’’ w’ wo x CG III (NPGR 010) - J. Křivánek 2015 r(x, w’)

Path tracing, v. 0. 1 (recursive form) get. Li (x, ω): y = nearest. Intersect (x, ω) return get. Le(y, –ω) + get. Lr (y, –ω) // emitted radiance // reflected radiance get. Lr(x, ωinc): [ωgen, pdfgen] = gen. Rnd. Dir. Brdf. Is(ωinc, normal(x) ) return 1/pdfgen * get. Li(x, ωgen) * brdf(x, ωinc, ωgen) * dot(normal(x), ωgen) CG III (NPGR 010) - J. Křivánek

Path tracing, v. 2012, Arnold Renderer © 2012 Columbia Pictures Industries, Inc. All Rights Reserved. CG III (NPGR 010) - J. Křivánek 2015

![Path tracing Kajiya 86 n Only one secondary ray at each intersection q n Path tracing [Kajiya 86] n Only one secondary ray at each intersection q n](https://slidetodoc.com/presentation_image_h/7309dd970a8a35badcfd818debd0b9b8/image-46.jpg)
Path tracing [Kajiya 86] n Only one secondary ray at each intersection q n Direct illumination: two strategies q q n n Random selection of interaction (diffuse reflection, refraction, etc. , …) Hope that the generated secondary ray hits the light source, or Explicitly pick a point on the light source Trace hundreds of paths through each pixel and average the result Advantage over distributed ray tracing: now branching of the ray tree means no explosion of the number of rays with recursion depth CG III (NPGR 010) - J. Křivánek 2015