Review Transformations CSE 681 Transformations Modeling transformations build

Review: Transformations CSE 681

Transformations • Modeling transformations • build complex models by positioning (transforming) simple components relative to each other • Viewing transformations • placing virtual camera in the world • transformation from world coordinates to camera coordinates • Perspective projection of 3 D coordinates to 2 D • Animation • vary transformations over time to create motion CSE 681

Transformations - Modeling CSE 681

Transformations - Viewing OBJECT WORLD CSE 681 CAMERA

Modeling Transformations Transform objects/points Transform coordinate system CSE 681

Affine Transformations Transform P = (x, y, z) to Q = (x’, y’, z’). Affine transformation: x’ = m 11 x + m 12 y + m 13 z + m 14 y’ = m 21 x + m 22 y + m 23 z + m 24 z’ = m 31 x + m 32 y + m 33 z + m 34 CSE 681

Translation by (tx, ty, tz): x’ = x + tx y’ = y + ty z’ = z + tz (tx, ty, tz) CSE 681

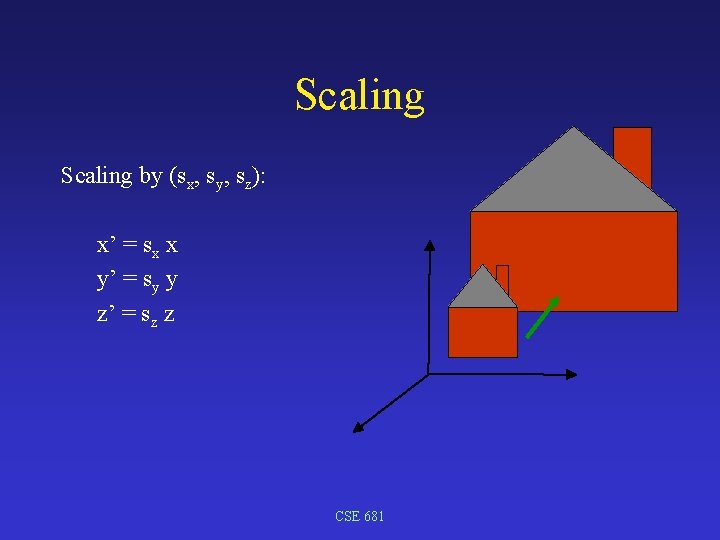
Scaling by (sx, sy, sz): x’ = sx x y’ = sy y z’ = sz z CSE 681

Rotation counter-clockwise by angle around the z-axis: x’ = x cos( ) – y sin( ) y y’ = x sin( ) + y cos( ) z’ = z r Proof: x = r cos( ) y = r sin( ) z r x x’ = r cos( + ) = r cos( ) – r sin( ) = x cos( ) – y sin( ) y’ = r sin( + ) = r cos( ) sin( ) + r sin( ) cos( ) = x sin( ) + y cos( ) CSE 681

Rotation around x-axis Rotation counter-clockwise by angle around the x-axis: x’ = x y’ = y cos( ) – z sin( ) z’ = y sin( ) + z cos( ) z x CSE 681 y

Rotation around y-axis Rotation counter-clockwise by angle around the y-axis: y’ = y z’ = z cos( ) – x sin( ) x x’ = z sin( ) + x cos( ) Or x’ = x cos( ) + z sin( ) y’ = y y z’ = – x sin( ) + z cos( ) CSE 681 z

Matrix Multiplication Scaling by (sx, sy, sz): x’ = sx x y’ = sy y z’ = sz z Rotation counter-clockwise by angle around the z-axis: x’ = x cos( ) – y sin( ) y’ = x sin( ) + y cos( ) z’ = z Translation by (tx, ty, tz): x’ = x + tx y’ = y + ty z’ = z + tz CSE 681

Homogeneous Coordinates Represent P by (x, y, z, 1) and Q by (x’, y’, z’, 1). (Homogeneous coordinates. ) Translation by (tx, ty, tz): x’ = x + tx y’ = y + ty z’ = z + tz Scaling by (sx, sy, sz): x’ = sx x y’ = sy y z’ = sz z CSE 681

Rotation Matrices Rotation counter-clockwise by angle around the x-axis: x’ = x y’ = y cos( ) – z sin( ) z’ = y sin( ) + z cos( ) Rotation counter-clockwise by angle around the y-axis: x’ = x cos( ) + z sin( ) y’ = y z’ = – x sin( ) + z cos( ) Rotation counter-clockwise by angle around the z-axis: x’ = x cos( ) – y sin( ) y’ = x sin( ) + y cos( ) z’ = z CSE 681

Affine Transformation Matrix Affine transformation: x’ = m 11 x + m 12 y + m 13 z + m 14 y’ = m 21 x + m 22 y + m 23 z + m 24 z’ = m 31 x + m 32 y + m 33 z + m 34 Transformation Matrix: CSE 681

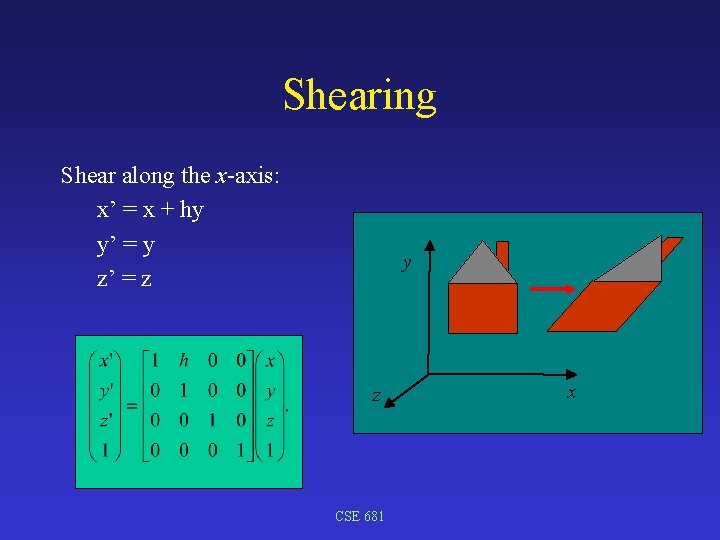
Shearing Shear along the x-axis: x’ = x + hy y’ = y z’ = z y z CSE 681 x

Reflection across the x-axis: x’ = (-1) x y’ = y z’ = z y z Reflection is a special case of scaling! CSE 681 x

Elementary Transformations • • Translation Rotation Scaling Shear What about inverses? CSE 681

Inverse Transformations Translation Scale Rotation Shear CSE 681

Compose Transformations y • Scale by (2, 1, 1) • Translate by (20, 5, 0) • Rotate by 30° counter-clockwise around the z-axis • Translate by (0, -50, 0) CSE 681 z x

Compose Transformation Matrices • Scale by (2, 1, 1); y • Translate by (20, 5, 0); • Rotate by 30° counter-clockwise around the z-axis; Translate x z • Translate by (0, -50, 0). Rotate CSE 681 Translate Scale

Compose Transformation Matrices • Scale by (2, 1, 1); y • Translate by (20, 5, 0); • Rotate by 30° counter-clockwise around the z-axis; z • Translate by (0, -50, 0). CSE 681 x

Order Matters! Transformations are not necessarily commutative! • Translate by (20, 0, 0). • Rotate by 30. • Translate by (20, 0, 0). y z y x z CSE 681 x

Order of Transformation Matrices Apply transformation matrices from right to left. • Translate by (20, 0, 0). • Rotate by 30. • Translate by (20, 0, 0). CSE 681

Which transformations commute? • • • Translation and translation? Scaling and scaling? Rotation and rotation? Translation and scaling? Translation and rotation? Scaling and rotation? CSE 681

Elementary Transformations Elementary transformations: • Translation; • Rotation; • Scaling; • Shear. Theorem: Every affine transformation can be decomposed into elementary operations. Euler’s Theorem: Every rotation around the origin can be decomposed into a rotation around the x-axis followed by a rotation around the y-axis followed by a rotation around the z-axis. (or a single rotation about an arbitrary axis). CSE 681

Vectors Vector V = (Vx, Vy, Vz). Homogeneous coordinates: (Vx, Vy, Vz, 0). Affine transformation: CSE 681

Vectors Rotation: Scaling: Translation: (Note: No change. ) CSE 681

Transform Parametric Line u P 0 V P(u) M M M u Q(u) Q 0 CSE 681 W

Line transformed point on a line ? = point on transformed line M(P(u) T) ? = M(P 0 T + u* VT) Line through P 0 = (x, y, z, 1) in direction V = (Vx, Vy, Vz, 0): P(u) = P 0 T + u* VT {(x 0, y 0, z 0, 1) + u* (Vx, Vy, Vz, 0): u Reals}. Apply affine transformation matrix M to line P(u): M *P(u) = { M (P 0 T + u VT) : u Reals} = { M P 0 T + u. M VT : u Reals} = { Q 0 + u V’ : u Reals}. Theorem: Affine transformations transform lines to lines. CSE 681

Affine Transformation of Lines y y z x z CSE 681 x

Affine Combinations R b Q a P M M b M Q’ a R’ P’ CSE 681

Affine Combinations Affine combinations of P = (x, y, z, 1) and Q = (x’, y’, z’, 1): {R = a (x, y, z, 1) + b (x’, y’, z’, 1): a, b Reals and a + b = 1} Apply affine transformation matrix M to (a PT + b QT) gives: M (a PT + b QT) = M a PT + M b QT = a M P T + b M QT = a P’ + b Q’ = MR = R’ Theorem: Affine transformations preserve affine combinations. CSE 681

Properties of Affine Transformations • • • Affine transformations map lines to lines; Affine transformations preserve affine combinations; Affine transformations preserve parallelism; Affine transformations change volume by | Det(M) |; Any affine transformation can be decomposed into elementary transformations. • Affine transformations [does/does not] preserve angles? • Affine transformations [does/does not] preserve the intersection of two lines? • Affine transformations [does/does not] preserve distances? CSE 681

Properties of Transformation Matrices First column is how (1, 0, 0, 0) transforms Second column is how (0, 1, 0, 0) transforms Third column is how (0, 0, 1, 0) transforms Matrix holds how coordinate axes transform and how origin transforms CSE 681

Properties of Pure Rotation Matrices Rows (columns) are orthogonal to each other A row dot product any other row = 0 Each row (column) dot product times itself = 1 RT = R-1 CSE 681

Coordinate Frame y j i k x z • Coordinate frame is given by origin and three mutually orthogonal unit vectors, i, j, k - defined in (x, y, z) space • Mutually orthogonal (dot products): i • j = ? ; i • k = ? ; j • k = ? . • Unit vectors (dot products): i • i = ? ; j • j = ? ; k • k = ? . CSE 681

Orientation Right handed coordinate system: Left handed coordinate system: y y z z x (Into page) x (Out of page) CSE 681

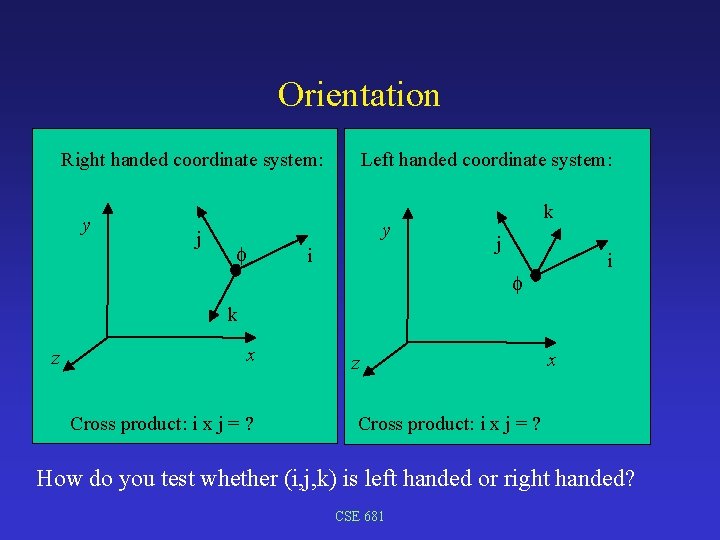
Orientation Right handed coordinate system: y j Left handed coordinate system: y i k j i k z x Cross product: i x j = ? How do you test whether (i, j, k) is left handed or right handed? CSE 681

Coordinate Transformations y j i k x z Given object data points defined in the (i, j, k, ) coordinate frame, Given the definition of (i, j, k, ) in (x, y, z) coordinates, How do you determine the coordinates of the object data points in the (x, y, z, 0) frame? CSE 681

Coordinate change (Translation) b y ( x, y, z) a (0, 0, 0) c z Change from (a, b, c, ) coordinates to (x, y, z, 0) coordinates: 1. 2. Move (a, b, c, ) to (x, y, z, 0) and invert Move data relative from (0, 0, 0) out to position by adding CSE 681 x

Coordinate change (Rotation) b x y ( x, y, z) (0, 0, 0) c a z Change from (a, b, c, ) coordinates to (x, y, z, 0) coordinates: 1. 2. z-axis rotation by Rotate (a, b, c) by and invert Rotate data by - CSE 681

Object Transformations y j i j z i k x k Given (i, j, k, p) defined in the (x, y, z, 0) coordinate frame, Transform points defined in the (i, j, k, ) coordinate frame to the (x, y, z, 0) coordinate frame. Rotate object to get x to line up with i, then translate to é ê ê ë 1 0 0 0 0 1 0 x ù y ú ú. z ú ú 1û CSE 681

Object Transformations y j i j z i k x k Affine transformation matrix: CSE 681

Coordinate Transformations y j i k x z Given (i, j, k, ) defined in the (x, y, z, 0) coordinate frame, Transform points in (i, j, k, 0) coordinate frame to (x, y, z, ) coordinate frame. translate by - , then rotate to align i with x – then invert CSE 681

Coordinate Transformations y j i k x z T= R= CSE 681

Coordinate Transformations y j i k x z Apply RT to coordinate system Apply (RT)-1 to data = T-1 R-1 Affine transformation matrix: CSE 681

Composition of coordinate change y y’ y” M 1 z M 2 x’ ’ 0 z” x z’ x” M 1 changes from coordinate frame (x, y, z, ) to (x’, y’, z’, ’). M 2 changes from coordinate frame (x’, y’, z’, ’) to (x’’, y’’, z’’, ’’). Change from coordinate frame (x, y, z, ) to (x’’, y’’, z’’, 0): ? CSE 681

Composition of transformations - example B’ y A x CSE 681 B

Transformations of normal vectors n n is a unit normal vector to plane . M is an affine transformation matrix. How is n transformed, to keep it perpendicular to the plane, under: • translation? • rotation by ? • uniform scaling by s? • shearing or non-uniform scaling? CSE 681

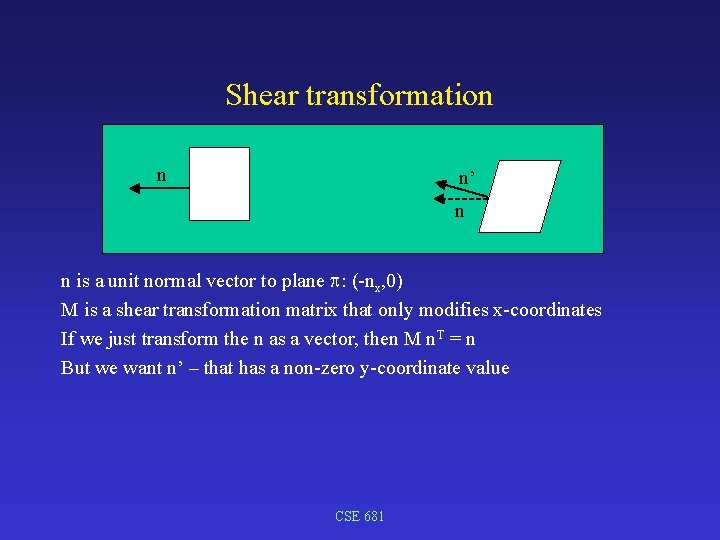
Shear transformation n n’ n n is a unit normal vector to plane : (-nx, 0) M is a shear transformation matrix that only modifies x-coordinates If we just transform the n as a vector, then M n. T = n But we want n’ – that has a non-zero y-coordinate value CSE 681

Transformations of normal vectors Planar equation: a x + b y + c z + d = 0. Let N = (a, b, c, d). (Note: (a, b, c) is normal vector) n Let P = (x, y, z, 1) be a point in plane . Planar equation: N • P = 0. P T M is an affine transformation matrix. (M is M transpose. ) Let P’ = M PT. Find N’ such that N’ • P’ = 0 (transformed planar equation) N • P = 0; N PT = 0; N (M-1 M) PT = 0; (N M-1) (M PT) = 0; (N M-1) P’T = 0; So N’ = NM-1 To put in column-vector form, (N’)T = (NM-1)T = (M-1)TNT So N’ = ((M-1)T NT)T and (M-1)T is the transformation matrix to take NT into N’T Note: If M is a rotation matrix, (M-1)T = M. CSE 681