Rendering Pipeline 3 D Polygon Rendering n Many

Rendering Pipeline

3 D Polygon Rendering n Many applications use rendering of 3 D polygons with direct illumination 2

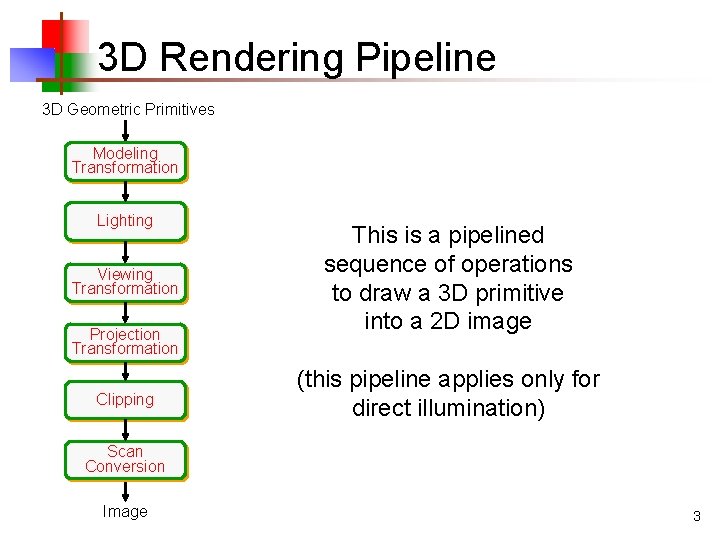
3 D Rendering Pipeline 3 D Geometric Primitives Modeling Transformation Lighting Viewing Transformation Projection Transformation Clipping This is a pipelined sequence of operations to draw a 3 D primitive into a 2 D image (this pipeline applies only for direct illumination) Scan Conversion Image 3

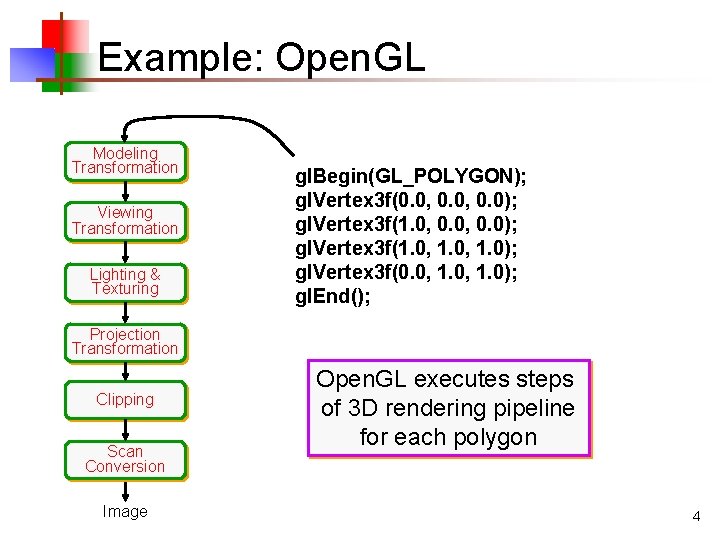
Example: Open. GL Modeling Transformation Viewing Transformation Lighting & Texturing gl. Begin(GL_POLYGON); gl. Vertex 3 f(0. 0, 0. 0); gl. Vertex 3 f(1. 0, 1. 0); gl. Vertex 3 f(0. 0, 1. 0); gl. End(); Projection Transformation Clipping Scan Conversion Image Open. GL executes steps of 3 D rendering pipeline for each polygon 4

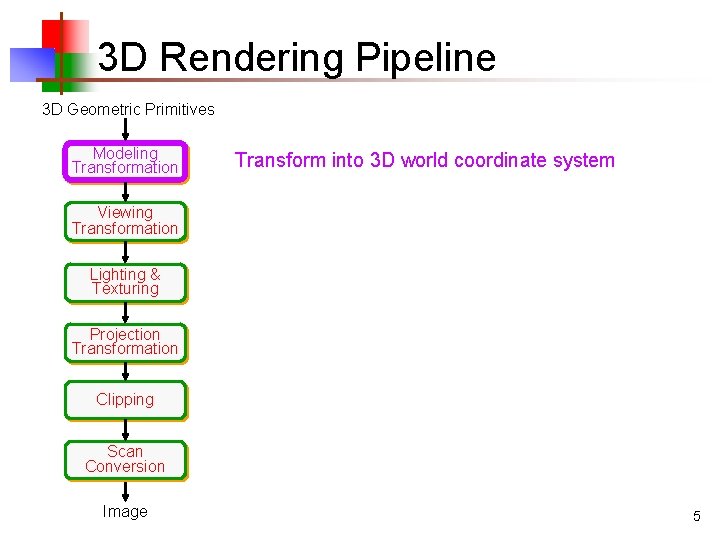
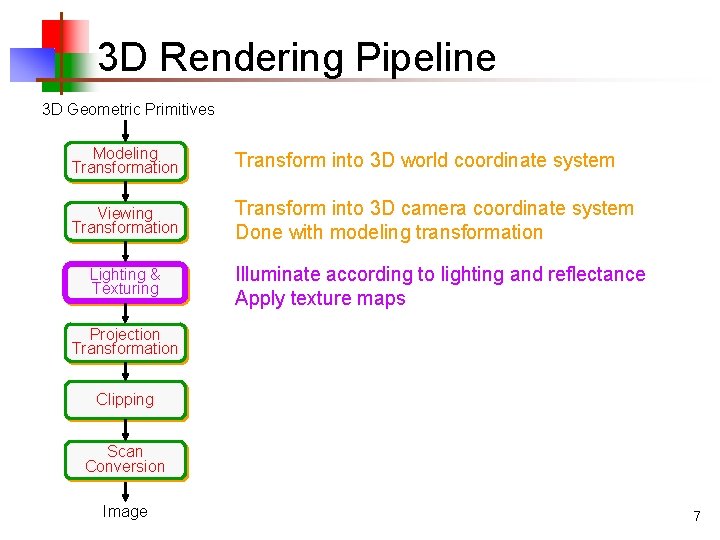
3 D Rendering Pipeline 3 D Geometric Primitives Modeling Transformation Transform into 3 D world coordinate system Viewing Transformation Lighting & Texturing Projection Transformation Clipping Scan Conversion Image 5

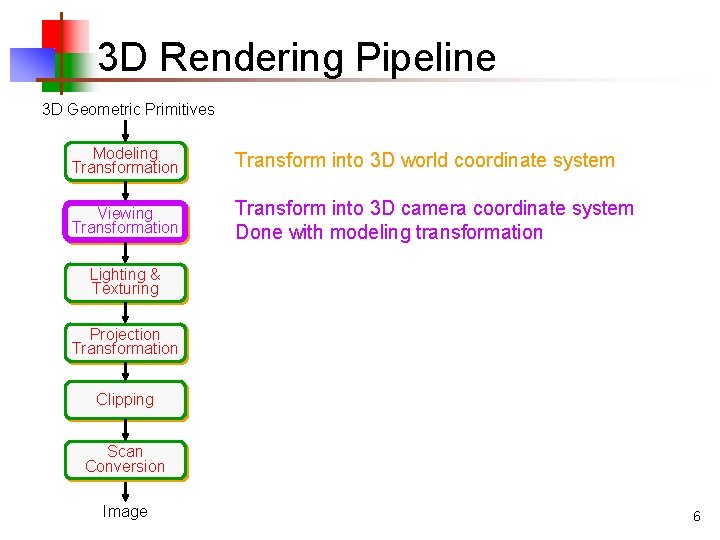
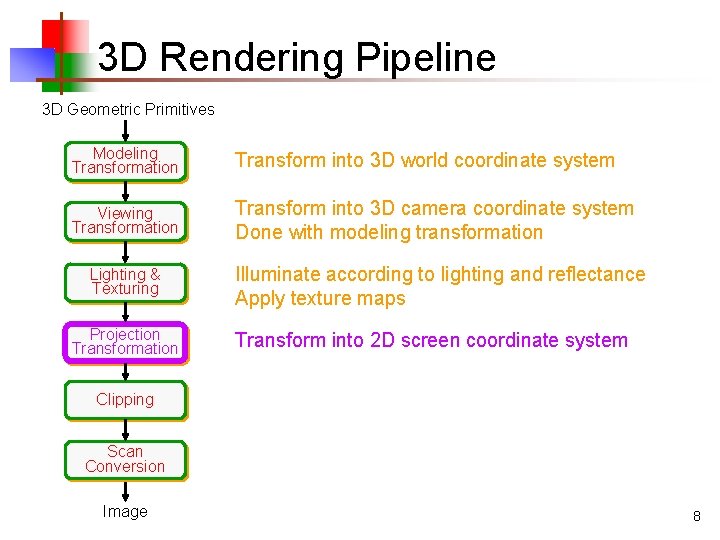
3 D Rendering Pipeline 3 D Geometric Primitives Modeling Transformation Transform into 3 D world coordinate system Viewing Transformation Transform into 3 D camera coordinate system Done with modeling transformation Lighting & Texturing Projection Transformation Clipping Scan Conversion Image 6

3 D Rendering Pipeline 3 D Geometric Primitives Modeling Transformation Transform into 3 D world coordinate system Viewing Transformation Transform into 3 D camera coordinate system Done with modeling transformation Lighting & Texturing Illuminate according to lighting and reflectance Apply texture maps Projection Transformation Clipping Scan Conversion Image 7

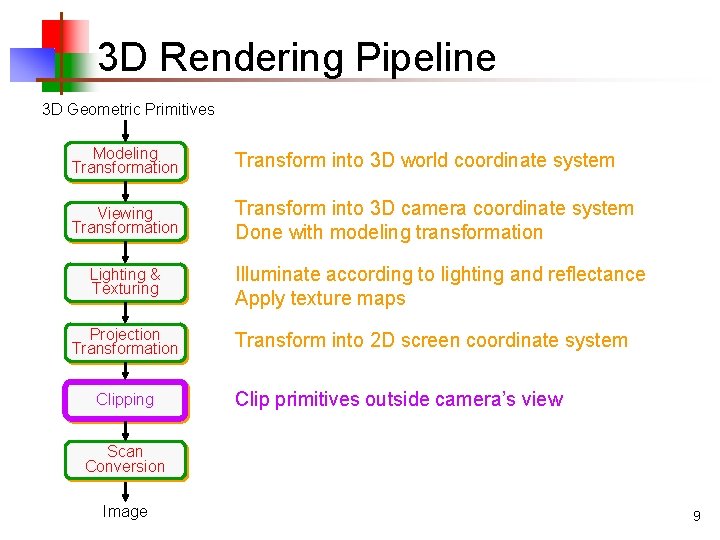
3 D Rendering Pipeline 3 D Geometric Primitives Modeling Transformation Transform into 3 D world coordinate system Viewing Transformation Transform into 3 D camera coordinate system Done with modeling transformation Lighting & Texturing Projection Transformation Illuminate according to lighting and reflectance Apply texture maps Transform into 2 D screen coordinate system Clipping Scan Conversion Image 8

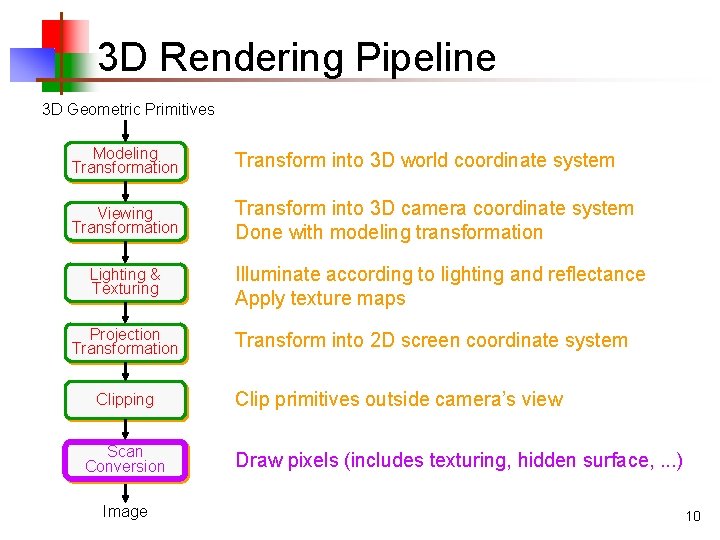
3 D Rendering Pipeline 3 D Geometric Primitives Modeling Transformation Transform into 3 D world coordinate system Viewing Transformation Transform into 3 D camera coordinate system Done with modeling transformation Lighting & Texturing Projection Transformation Clipping Illuminate according to lighting and reflectance Apply texture maps Transform into 2 D screen coordinate system Clip primitives outside camera’s view Scan Conversion Image 9

3 D Rendering Pipeline 3 D Geometric Primitives Modeling Transformation Transform into 3 D world coordinate system Viewing Transformation Transform into 3 D camera coordinate system Done with modeling transformation Lighting & Texturing Projection Transformation Clipping Scan Conversion Image Illuminate according to lighting and reflectance Apply texture maps Transform into 2 D screen coordinate system Clip primitives outside camera’s view Draw pixels (includes texturing, hidden surface, . . . ) 10

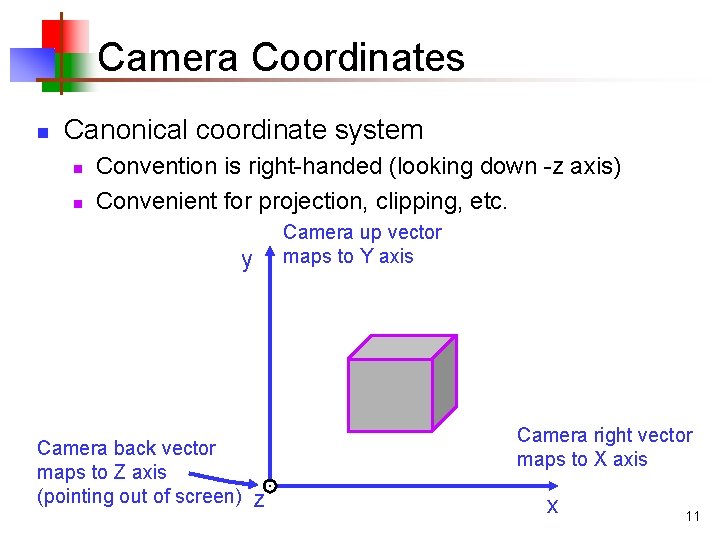
Camera Coordinates n Canonical coordinate system n n Convention is right-handed (looking down -z axis) Convenient for projection, clipping, etc. Camera up vector maps to Y axis y Camera back vector maps to Z axis (pointing out of screen) Camera right vector maps to X axis z x 11

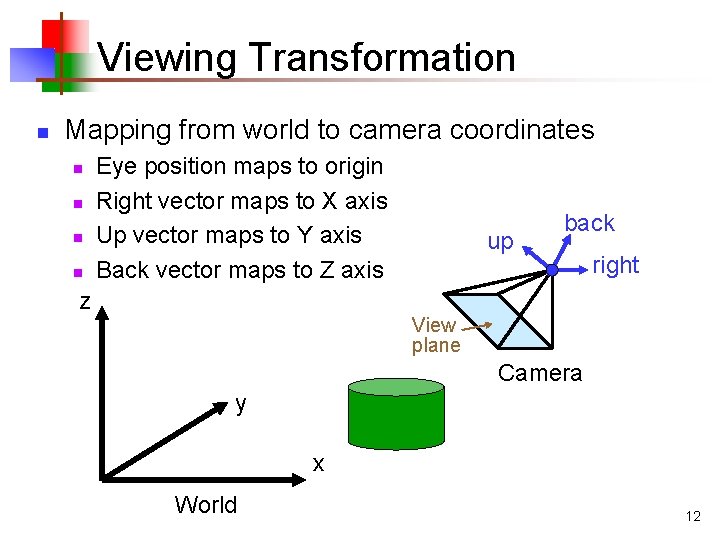
Viewing Transformation n Mapping from world to camera coordinates n n Eye position maps to origin Right vector maps to X axis Up vector maps to Y axis Back vector maps to Z axis z up back right View plane Camera y x World 12

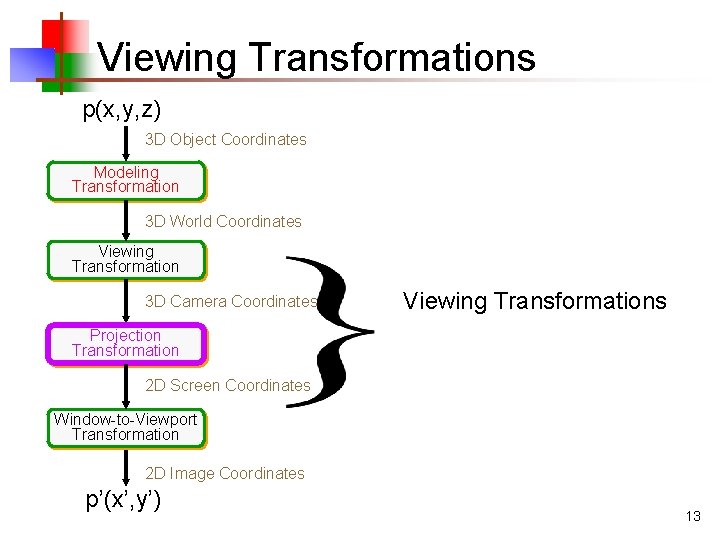
Viewing Transformations p(x, y, z) 3 D Object Coordinates Modeling Transformation 3 D World Coordinates Viewing Transformation 3 D Camera Coordinates Viewing Transformations Projection Transformation 2 D Screen Coordinates Window-to-Viewport Transformation 2 D Image Coordinates p’(x’, y’) 13

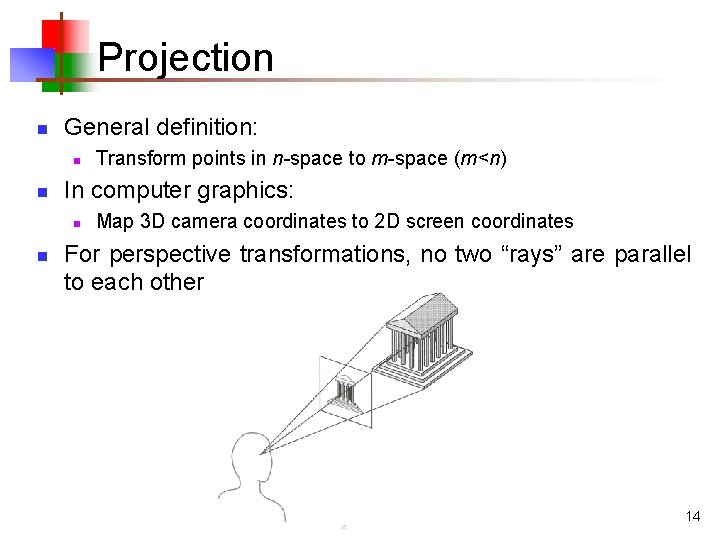
Projection n General definition: n n In computer graphics: n n Transform points in n-space to m-space (m<n) Map 3 D camera coordinates to 2 D screen coordinates For perspective transformations, no two “rays” are parallel to each other 14

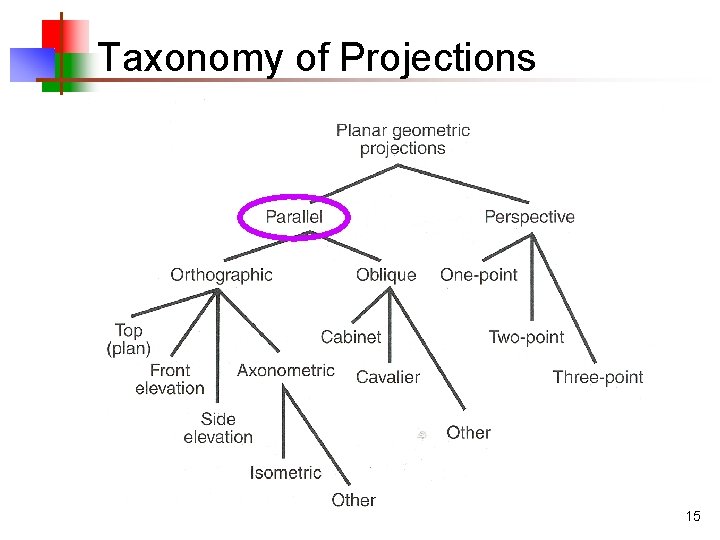
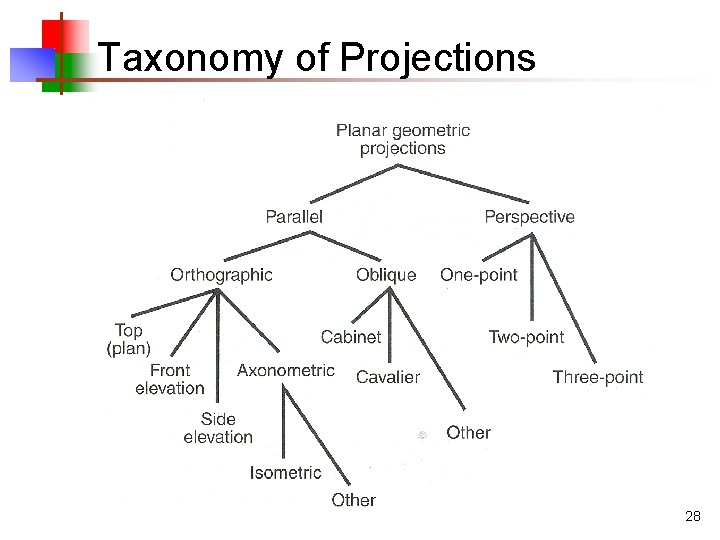
Taxonomy of Projections 15

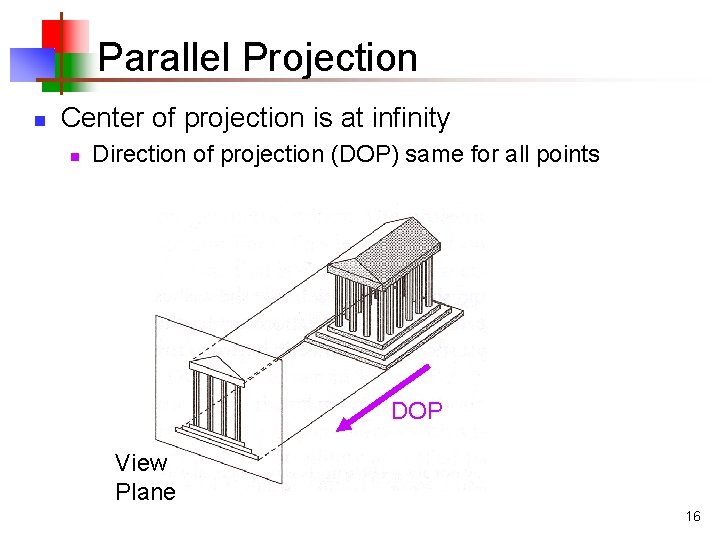
Parallel Projection n Center of projection is at infinity n Direction of projection (DOP) same for all points DOP View Plane 16

Orthographic Projections n DOP perpendicular to view plane Front Top Side 17

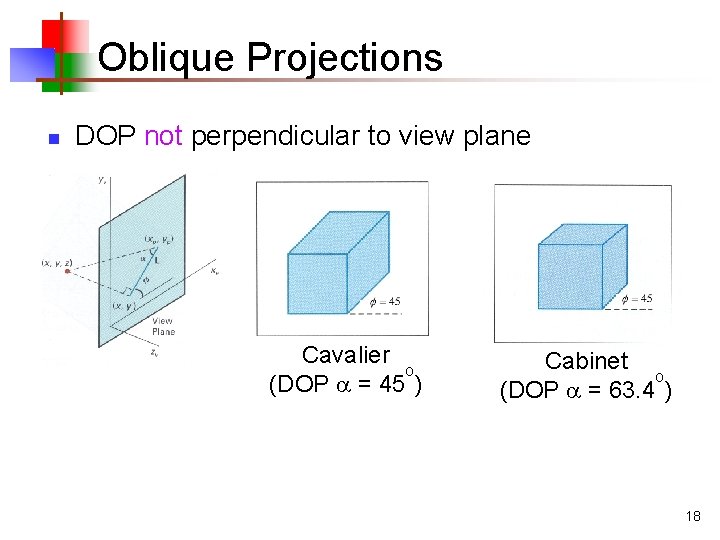
Oblique Projections n DOP not perpendicular to view plane Cavalier o (DOP = 45 ) Cabinet o (DOP = 63. 4 ) 18

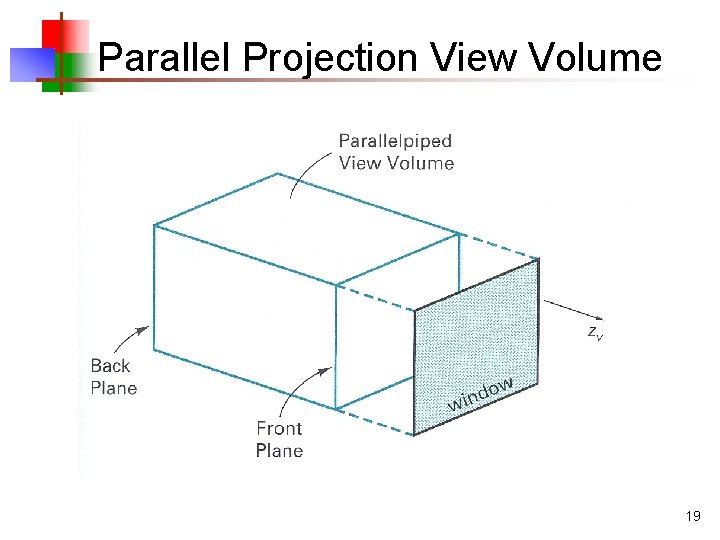
Parallel Projection View Volume 19

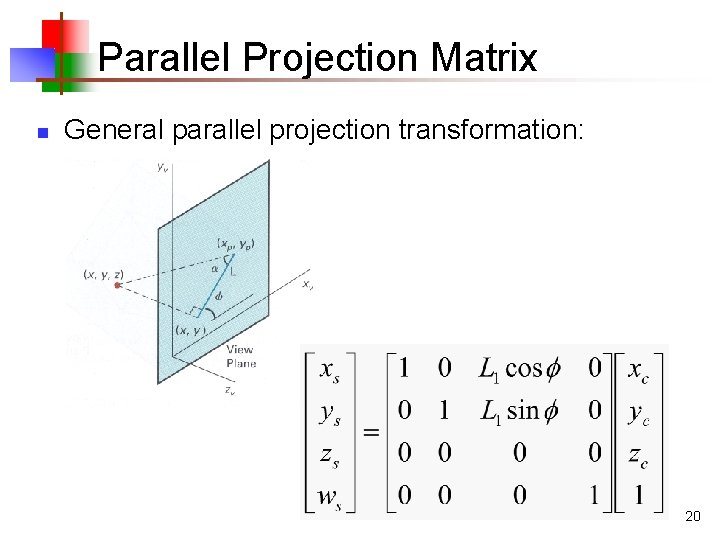
Parallel Projection Matrix n General parallel projection transformation: 20

Taxonomy of Projections 21

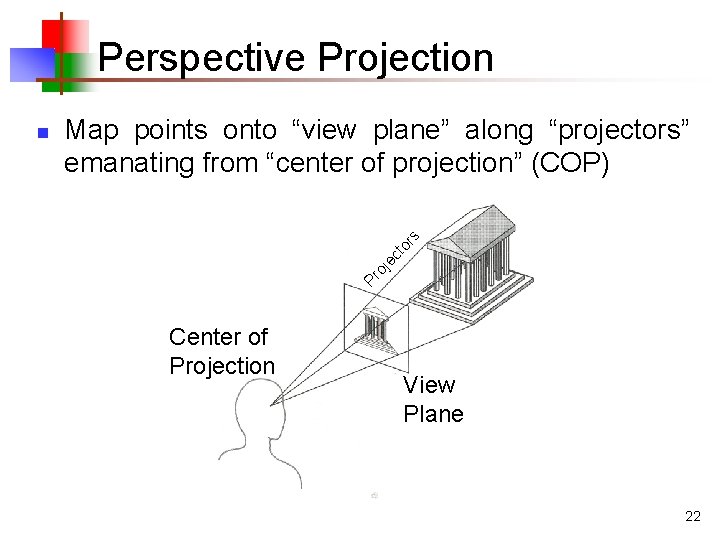
Perspective Projection oj ec to rs Map points onto “view plane” along “projectors” emanating from “center of projection” (COP) Pr n Center of Projection View Plane 22

Perspective Projection n How many vanishing points? 3 -Point Perspective n 2 -Point Perspective 1 -Point Perspective The difference is how many of the three principle directions are parallel/orthogonal to the projection plane 23

Perspective Projection View Volume View Plane 24

Camera to Screen n n Remember: Object Camera Screen Just like raytracer n n “screen” is the z=d plane for some constant d Origin of screen coordinates is (0, 0, d) Its x and y axes are parallel to the x and y axes of the eye coordinate system All these coordinates are in camera space now 25

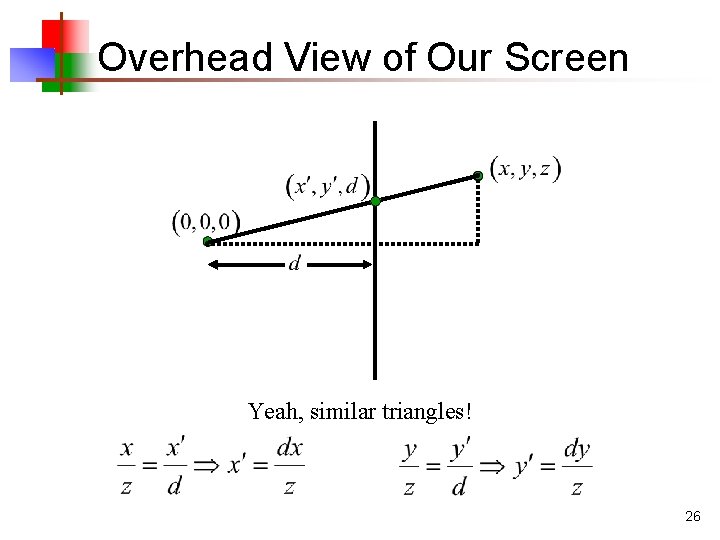
Overhead View of Our Screen Yeah, similar triangles! 26

The Perspective Matrix n n n This “division by z” can be accomplished by a 4 x 4 matrix too! What happens to the point (x, y, z, 1)? What point coordinates? is this in non-homogeneous 27

Taxonomy of Projections 28

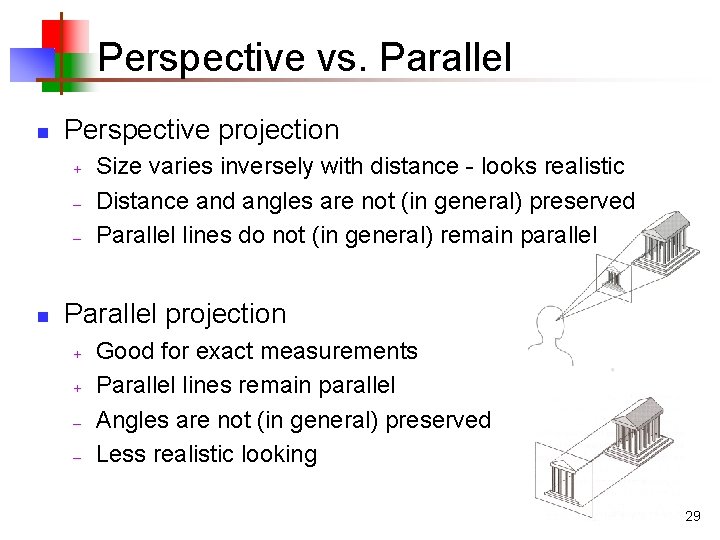
Perspective vs. Parallel n Perspective projection + – – n Size varies inversely with distance - looks realistic Distance and angles are not (in general) preserved Parallel lines do not (in general) remain parallel Parallel projection + + – – Good for exact measurements Parallel lines remain parallel Angles are not (in general) preserved Less realistic looking 29

Classical Projections 30

Viewing in Open. GL n n n Open. GL has multiple matrix stacks – transformation functions right-multiply the top of the stack Two most important stacks: GL_MODELVIEW and GL_PROJECTION Points get multiplied by the modelview matrix first, and then the projection matrix GL_MODELVIEW: Object->Camera GL_PROJECTION: Camera->Screen gl. Viewport(0, 0, w, h): Screen->Device 31

Summary n Camera transformation n Map 3 D world coordinates to 3 D camera coordinates Matrix has camera vectors as columns Projection transformation n n Map 3 D camera coordinates to 2 D screen coordinates Two types of projections: n n Parallel Perspective 32