ON THE ANALYSIS AND APPLICATION OF LDPC CODES

ON THE ANALYSIS AND APPLICATION OF LDPC CODES OLGICA MILENKOVIC UNIVERSITY OF COLORADO, BOULDER A joint work with: VIDYA KUMAR (Ph. D) STEFAN LAENDNER (Ph. D) DAVID LEYBA (Ph. D) VIJAY NAGARAJAN (MS) KIRAN PRAKASH (MS)

OUTLINE n n n n A brief introduction to codes on graphs An overview of known results: random-like codes for standard channel models Code structures amenable for practical implementation: structured LDPC codes Codes amenable for implementation with good error-floor properties Code design for non-standard channels ¨ Channels with memory ¨ Asymmetric channels Applying the turbo-decoding principle to classical algebraic codes: Reed-Solomon, Reed-Muller, BCH… Applying the turbo-decoding principle to systems with unequal errorprotection requirements

THE ERROR-CONTROL PARADIGM Noisy channels give rise to data errors: transmission or storage systems Need powerful error-control coding (ECC) schemes: linear or non-linear Linear EC Codes: Generated through simple generator or parity-check matrix Binary linear codes: Binary information vector (length k) Code vector (word): (length n) Key property: “Minimum distance of the code”, between two codewords Rate of the code R= k/n , smallest separation

LDPC CODES More than 40 years of research (1948 -1994) centered around Weights of errors that a code is guaranteed to correct “Bounded distance decoding” cannot achieve Shannon limit Trade-off minimum distance for efficient decoding Low-Density Parity-Check (LDPC) Codes Gallager 1963, Tanner 1984, Mac. Kay 1996 1. Linear block codes with sparse (small fraction of ones) parity-check matrix 2. Have natural representation in terms of bipartite graphs 3. Simple and efficient iterative decoding in the form of belief propagation (Pearl, 1980 -1990)

THE CODE GRAPH AND ITERATIVE DECODING Most important consequence of graphical description: efficient iterative decoding Message passing: Variable nodes: communicate to check nodes their reliability (log-likelihoods) Variable nodes Check nodes (Irregular degrees/codes) Check nodes: decide which variables are not reliable and “suppress” their inputs Small number of edges in graph = low complexity Nodes on left/right with constant degree: regular code Otherwise, codes termed irregular Can adjust “degree distribution” of variables/checks Best performance over standard channels: long, irregular, random-like LDPC codes Have proportional to length of code, but correct many more errors

DECODING OF LDPC CODES Iterative decoding optimal only if the code graph has no cycles Vardy et. al. 1997: All “good codes” must have cycles • What are desirable code properties? • Large girth (smallest cycle length): for sharp transition to waterfall region; large minimum distance; • Number of cycles of short length as small as possible; • Very low error-floors (girth-optimized graphs are not a very good choice Richardson 2003); • Make the performance capacity approaching: irregular degree distribution (depends on the channel, “safe” gap to capacity about 1 d. B); (Density Evolution, Richardson and Urbanke, 2001) • Practical applications: mathematical formula for positions of ones in H

HOW CAN ONE SATISFY THESE CONSTRAINTS? For “standard channels” (symmetric, binary-input) the questions are mostly well-understood BEC – considered to be a “closed case” (Capacity achieving degree distributions, complexity of decoding, stopping sets, have simple EXIT chart analysis…) Error-floor greatest remaining unsolved problem! For “non-standard” channels still a lot to work on

CODE CONSTRUCTION AND IMPLEMENTATION FOR STANDARD CHANNELS

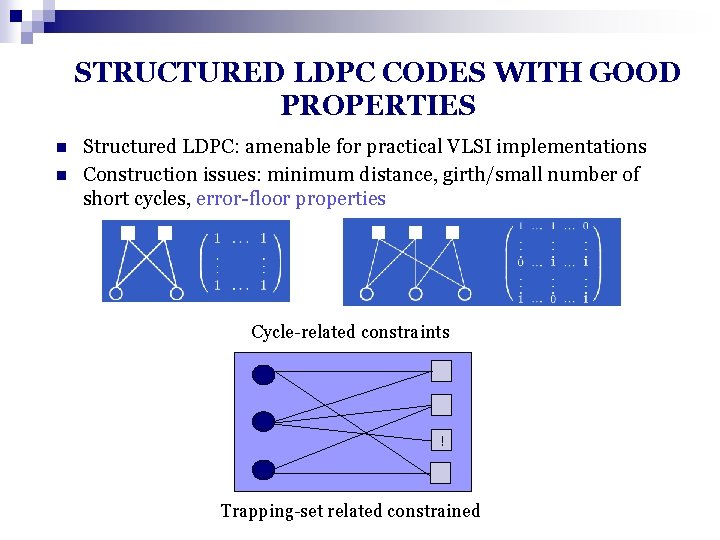
STRUCTURED LDPC CODES WITH GOOD PROPERTIES n n Structured LDPC: amenable for practical VLSI implementations Construction issues: minimum distance, girth/small number of short cycles, error-floor properties Cycle-related constraints ! Trapping-set related constrained

THE WATERFALL AND ERROR-FLOOR REGION Encyclopedia of Sparse Codes on Graphs: by D. Mac. Kay http: //www. inference. phy. cam. ac. uk/mackay/codes/data. html n n n Waterfall: Optimization of minimum distance and cycle length distribution (regular/irregular codes) Waterfall: Optimization of degree distribution and code construction Error floor: Optimization of trapping sets or … maybe a different decoding algorithm?

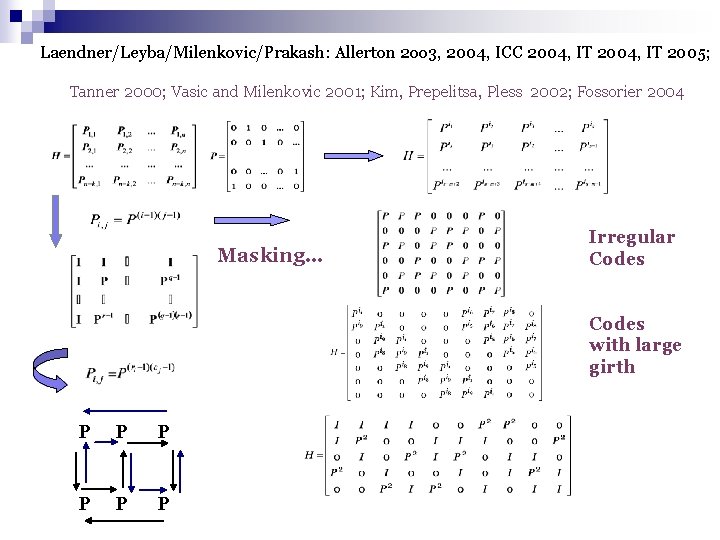
Laendner/Leyba/Milenkovic/Prakash: Allerton 2 oo 3, 2004, ICC 2004, IT 2005; Tanner 2000; Vasic and Milenkovic 2001; Kim, Prepelitsa, Pless 2002; Fossorier 2004 Masking… Irregular Codes with large girth P P P

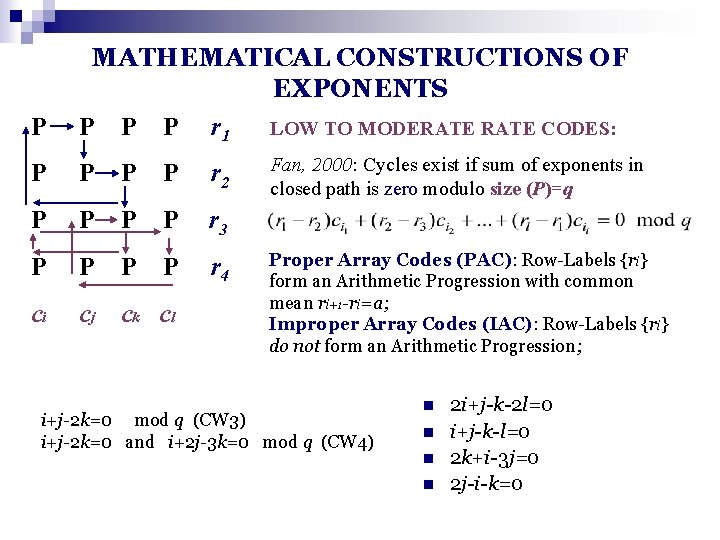
P MATHEMATICAL CONSTRUCTIONS OF EXPONENTS LOW TO MODERATE CODES: P P P r 1 P P r 2 P P r 3 P P r 4 ci cj ck cl Fan, 2000: Cycles exist if sum of exponents in closed path is zero modulo size (P)=q Proper Array Codes (PAC): Row-Labels {ri} form an Arithmetic Progression with common mean ri+1 -ri=a; Improper Array Codes (IAC): Row-Labels {ri} do not form an Arithmetic Progression; i+j-2 k=0 mod q (CW 3) i+j-2 k=0 and i+2 j-3 k=0 mod q (CW 4) n n 2 i+j-k-2 l=0 i+j-k-l=0 2 k+i-3 j=0 2 j-i-k=0

ANALYTICAL RESULTS ON ACHIEVABLE RATES n Number theoretic bounds for contructions: ¨ For PACs with girth g=8: ¨ For IACs with girth g=10: ¨ Results based on work of Bosznay, Erdos, Turan, Szemeredi, Bourgain s=1 0, 1, 3, 4, 9, 10, 12, 13, 27, 28, 30, 38, . . . s=2 0, 2, 3, 5, 9, 11, 12, 14, 27, 29, 30, 39, . . . s=3 0, 3, 4, 7, 9, 12, 13, 16, 27, 30, 35, 36, . . . s=1 0, 1, 5, 14, 25, 57, 88, 122, 198, 257, 280, . . . s=2 0, 2, 7, 18, 37, 65, 99, 151, 220, 233, 545, . . . s=3 0, 3, 7, 18, 31, 50, 105, 145, 186, 230, 289, . . . Mathematical constructions: Joint work with N. Kashyap, Queen’s , University, AMS Meeting, Chicago 2004

CYCLE-INVARIANT DIFFERENCE SETS n n n n n Definition: V an additive Abelian group, order v. (v, c, 1) difference set Ω in V is a c-subset of V with exactly one ordered pair (x, y) in Ω s. t. x-y=g, for a given g in. V. Examples: {1, 2, 4} mod 7, {0, 1, 3, 9} mod 13. “Incomplete” difference sets – not every element covered CIDS: Definition Elements of Ω arranged in ascending order. operator: cyclically shifts sequence i positions to the right For i = 1, …, m, (component-wise) are ordered difference sets as well Ω is an (m+1)-fold cycle invariant difference set over V Example: V=Z 7 and Ω ={1, 2, 4}, m=2 mod 7

CIDS – GENERALIZATION OF BOSE METHOD S= where constructed as is the primitive element of GF(q 2) , q odd prime Excellent performance for very low rate codes

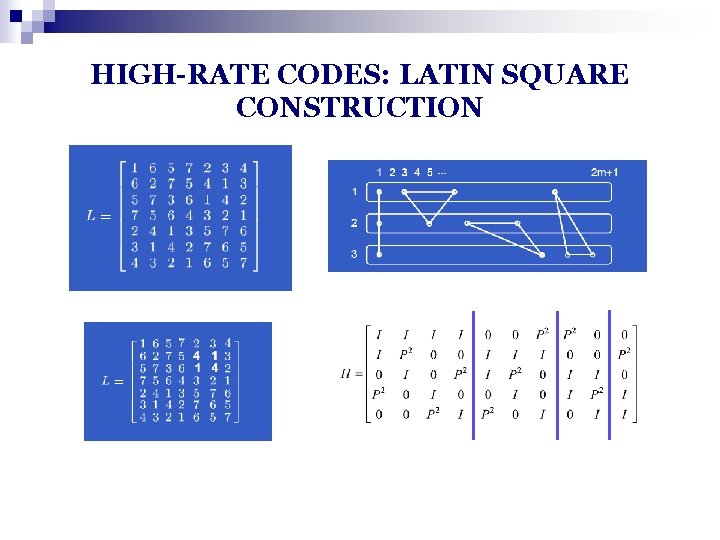
HIGH-RATE CODES: LATIN SQUARE CONSTRUCTION

ERROR FLOOR ANALYSIS n n n Near codewords (Neal/Mac. Kay, 2003) Trapping sets (Richardson, 2003) Considered to be the most outstanding problem in the area! Inherent property of both the decoding algorithm and code structure APPROACH: Try to predict error floor (Richardson, 2003, 2004), or Try to change the decoding algorithm Observations leading to new decoding algorithm: 1) Different computer codes give very different solutions; quantization has a very large influence on the error floor 2) Certain variables in the code graph show extremely large and uncontrolled jumps in likelihood values 3) Strange things happen when message values are very close to +1/-1

OBJECT OF INVESTIGATION: MARGULIS CODE n n Elementary trapping set (ETS): small subset of variable nodes for which induced subgraph has very few checks of odd degree INTUITION: channel noise configuration such that all variables in ETS are incorrect after certain number of iterations; small number of odd degree checks indicates that errors will not be easily corrected Margulis code: based on Cayley graphs (algebraic construction), has good girth Frame error rate curve has floor at 10 E-7, SNR=2. 4 d. B, AWGN Iteration number: 1 2 2 3 4 182 142 108 5 73 6 7 8 9 10 11 12 13 14 66 55 38 29 20 16 15 14 14 15 14 16 17 14 14 18 19 …. 14 14 14 …. Number of erroneous bits: At “freezing” point, all values of variable messages are +1/-1 and significant oscillations happen +1 → -1 Frozen activity lasts for 13 iterations: then “bad messages” propagate through the whole graph; can have jumps from -0. 33 to 49. 67

ALGORITHM FOR ELIMINATING THE ERROR FLOOR n n “Oscillations” reminiscent to problems encountered in theory of divergent series (G. H. Hardy, Divergent Series) Trick: use a low-complexity “extra-step” in sum-product algorithm based on result by Hardy Parameters tunable: when do you “start” using “extra-step”, what “numerical biases” should one use Can do density evolution analysis for optimization purposes – no loss expected in waterfall region (nor one observed) (Paper with S. Laendner, in preparation) 1000 good frames: Standard and modified message passing both take 7. 4 iterations on average for correct decoding Modified message passing never takes more than 16 iterations to converge 20 Bad frames (in MATLAB): Corrected 2/3 fraction of errors after 35, 41, 26, 119, 38, 98… iterations (standard failed even after 10000 iterations) Can use slightly more complicated result from G. H. H to reduce number of iteration to 20 -30

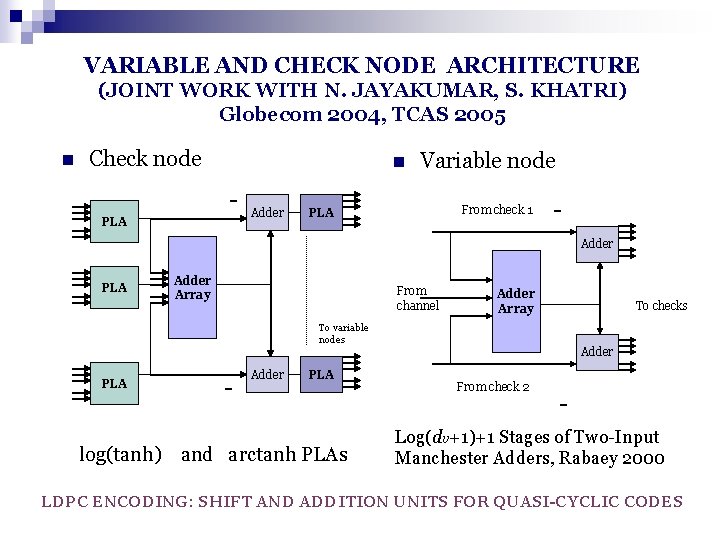
VARIABLE AND CHECK NODE ARCHITECTURE (JOINT WORK WITH N. JAYAKUMAR, S. KHATRI) Globecom 2004, TCAS 2005 n Check node n PLA Adder Variable node From check 1 PLA Adder Array From channel Adder Array To checks To variable nodes PLA - Adder PLA log(tanh) and arctanh PLAs Adder From check 2 - Log(dv+1)+1 Stages of Two-Input Manchester Adders, Rabaey 2000 LDPC ENCODING: SHIFT AND ADDITION UNITS FOR QUASI-CYCLIC CODES

ADVANTAGES OF NETWORK OF PLA ARCHITECTURE n n n n Logic function in 2 -level form: good delay characteristics as long as size of each PLA is bounded (Khatri, Brayton, Sangoivani-Vincentelli, 2000) Standard cell implementation: considerable delay in traversing the different levels (i. e. gates) Local wiring collapsed into compact 2 -level core: crosstalk-immunity local wiring delays are reduced Devices in PLA core are minimum-sized: compact layouts NMOS devices used exclusively: devices placed extremely close together In a standard cell layout, both PMOS and NMOS devices are present in each cell: PMOS-to-NMOS diffusion spacing requirement results in loss of layout density PLAs dynamic: faster than static standard cell implementation Can easily accommodate re-configurability requirement

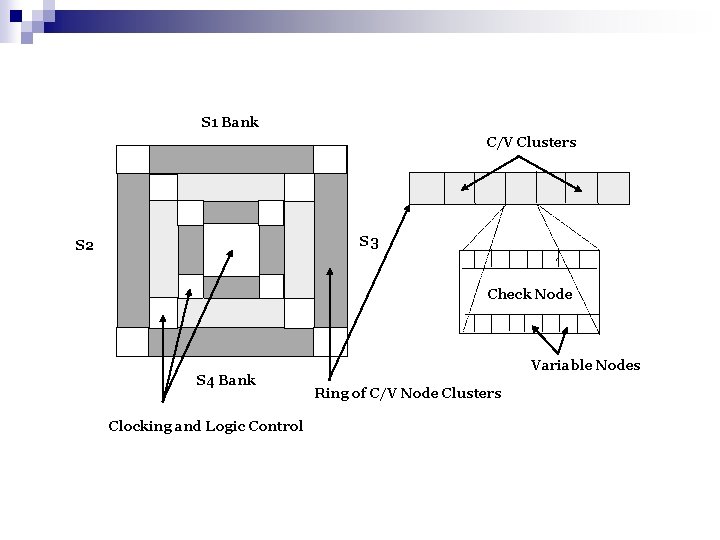
S 1 Bank C/V Clusters S 3 S 2 Check Node S 4 Bank Clocking and Logic Control Variable Nodes Ring of C/V Node Clusters

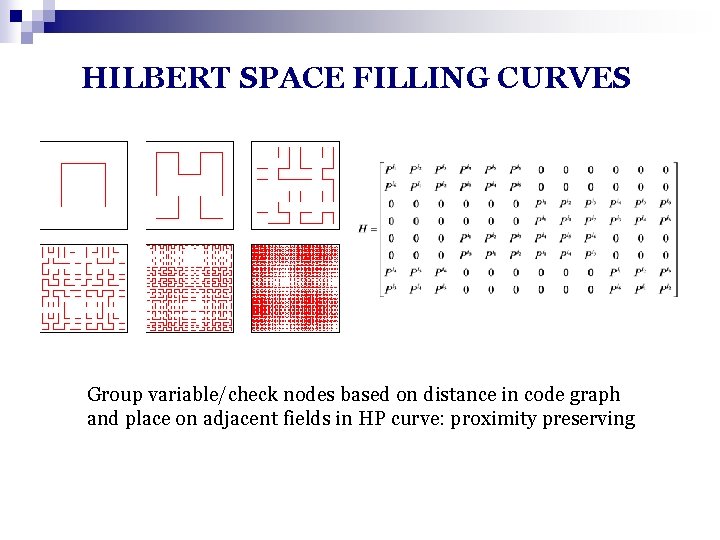
HILBERT SPACE FILLING CURVES Group variable/check nodes based on distance in code graph and place on adjacent fields in HP curve: proximity preserving

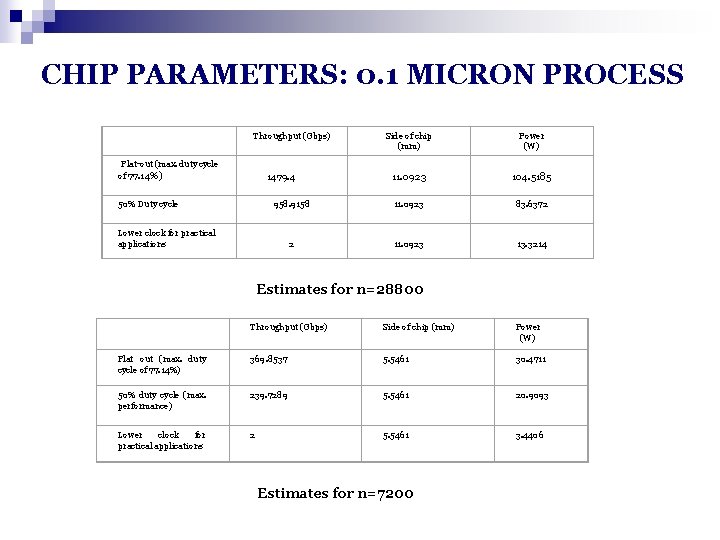
CHIP PARAMETERS: 0. 1 MICRON PROCESS Throughput (Gbps) Flat-out (max. duty cycle of 77. 14%) Side of chip (mm) Power (W) 11. 0923 104. 5185 958. 9158 11. 0923 83. 6372 2 11. 0923 13. 3214 1479. 4 50% Duty cycle Lower clock for practical applications Estimates for n=28800 Throughput (Gbps) Side of chip (mm) Power (W) Flat out (max. duty cycle of 77. 14%) 369. 8537 5. 5461 30. 4711 50% duty cycle (max. performance) 239. 7289 5. 5461 20. 9093 Lower clock for practical applications 2 5. 5461 3. 4406 Estimates for n=7200

LDPC CODES FOR NON-STANDARD CHANNELS

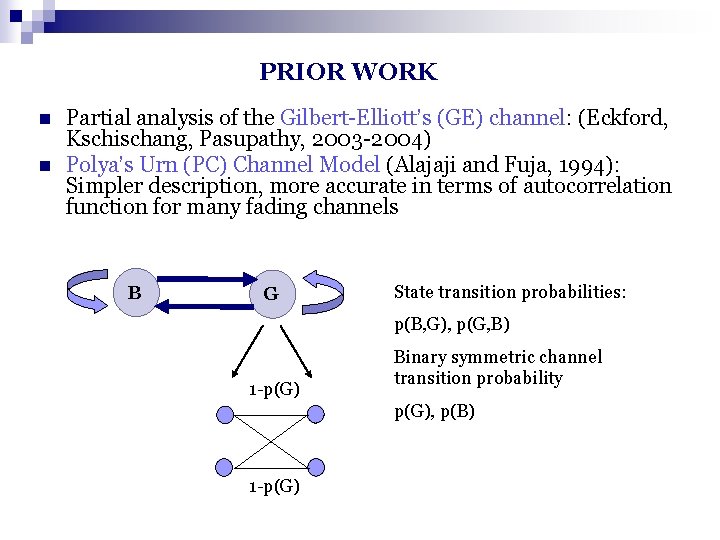
PRIOR WORK n n Partial analysis of the Gilbert-Elliott’s (GE) channel: (Eckford, Kschischang, Pasupathy, 2003 -2004) Polya’s Urn (PC) Channel Model (Alajaji and Fuja, 1994): Simpler description, more accurate in terms of autocorrelation function for many fading channels B G State transition probabilities: p(B, G), p(G, B) 1 -p(G) Binary symmetric channel transition probability p(G), p(B) 1 -p(G)

FINITE MEMORY POLYA URN CHANNEL n n Binary additive channel with memory Occurrence of error increases probability of future errors Output sample at time i (Yi) is modulo-two sum of input Xi and noise sequence Zi , where {Xi} and {Zi} are independent sequences The noise process is formed based on the following scheme: Noise samples are outcomes of consecutive draws from urn, and Zi is one if ith ball was red and zero if black n n Stationary, ergodic channel with memory M Three parameters: (σ, δ, M), where ρ=R/T < ½ , σ = 1 - ρ = S/T and δ = Δ/T

M=1 PC CHANNEL (DEMONSTRATIVE EXAMPLE) n n Reduced 2 -parameter space a = (σ + δ)/(1+ δ) and b = (1 - σ + δ)/( 1+ δ) A two-state Markov chain with states S 0 and S 1 transition probabilities 1 -a and 1 -b Channel transition matrix is n State S 0 corresponds to a noise sample of value zero, and state S 1 to one n Observation: this type of channel is not included in the GE analysis by Eckford et. al. Nagarajan and Milenkovic, IEEE CCEC, 2004

JOINT DECODING/CHANNEL STATE ESTIMATION n Use extrinsic information from the decoder to improve the quality of the estimate of the channel state and vice-versa

BCJR EQUATIONS FOR PC CHANNEL ESTIMATION n Forward message vector n Backward message vector n Channel information passed to decoder

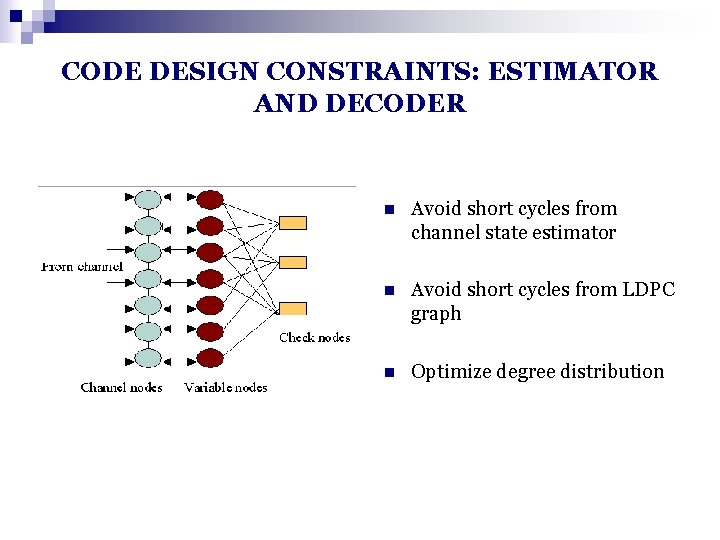
CODE DESIGN CONSTRAINTS: ESTIMATOR AND DECODER n Avoid short cycles from channel state estimator n Avoid short cycles from LDPC graph n Optimize degree distribution

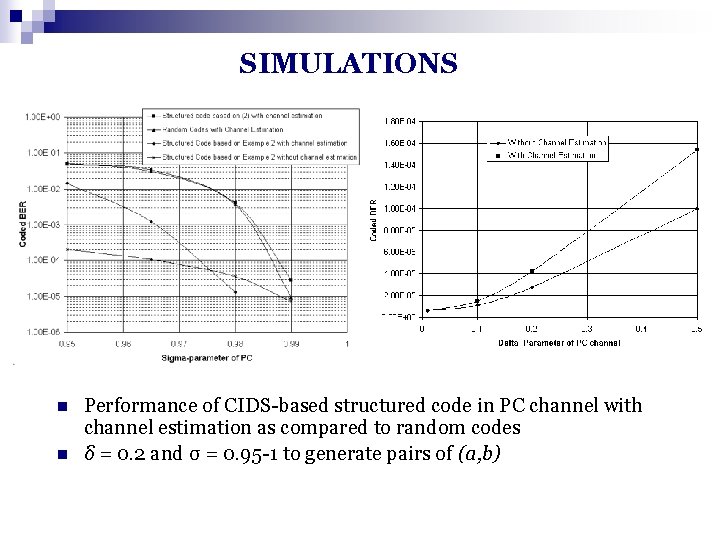
SIMULATIONS n n Performance of CIDS-based structured code in PC channel with channel estimation as compared to random codes δ = 0. 2 and σ = 0. 95 -1 to generate pairs of (a, b)

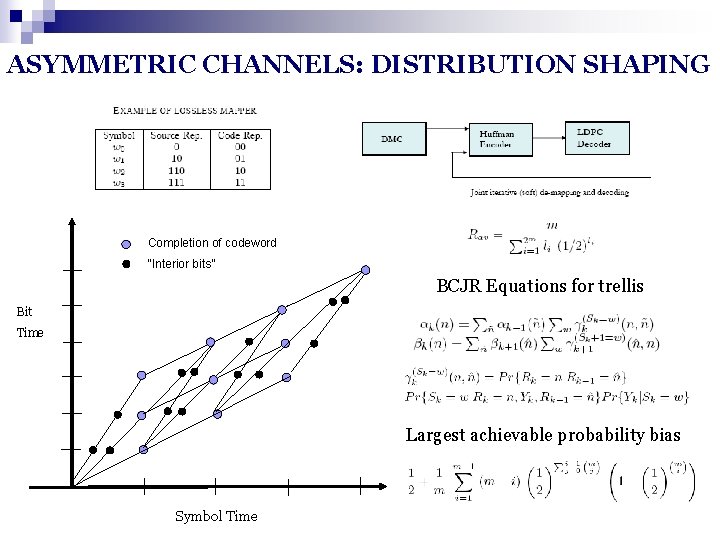
ASYMMETRIC CHANNELS: DISTRIBUTION SHAPING Gallager 1968: Linear codes can achieve capacity on any Discrete Memoryless Channel (DMC) when combined with “distribution shapers” Mapping not 1 -1 Rate loss? Mc. Eliece, 2001: Attempts to use this scheme with Repeat-Accumulate or LDPC codes failed Biggest obstacle: cannot do “soft” de-mapping Solution: Use soft Huffman encoding (extension of idea by Hagenauer et. al. for joint source-channel coding) In preparation: Leyba, Milenkovic 2005

ASYMMETRIC CHANNELS: DISTRIBUTION SHAPING Completion of codeword “Interior bits” BCJR Equations for trellis Bit Time Largest achievable probability bias Symbol Time

ITERATIVE DECODING OF CLASSICAL ALGEBRAIC CODES APPLICATIONS FOR UNEQUAL ERROR PROTECTION

GRAPHICAL REPRESENTATIONS OF ALGEBEBRAIC CODES n Consider a [7, 4, 3] Hamming code n Idea put forward by Yedidia, Fossorier Support Sets: S 1={4, 5, 6, 7}; S 2={2, 3, 6, 7}; Intersection Set n n ={6, 7} Set entries corresponding to in these two rows to zero; insert new column with non-zero entries in these two rows; call this an auxiliary variable Insert a new row with non-zero entries at positions indexed by

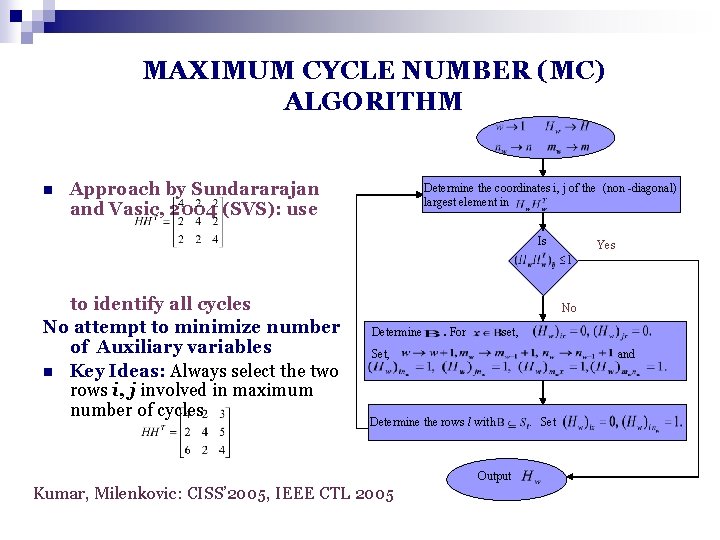
MAXIMUM CYCLE NUMBER (MC) ALGORITHM n Approach by Sundararajan and Vasic, 2004 (SVS): use Determine the coordinates i, j of the (non -diagonal) largest element in Is to identify all cycles No attempt to minimize number of Auxiliary variables n Key Ideas: Always select the two rows i, j involved in maximum number of cycles Yes No Determine . For set, Set, and Determine the rows l with Output Kumar, Milenkovic: CISS’ 2005, IEEE CTL 2005 . Set

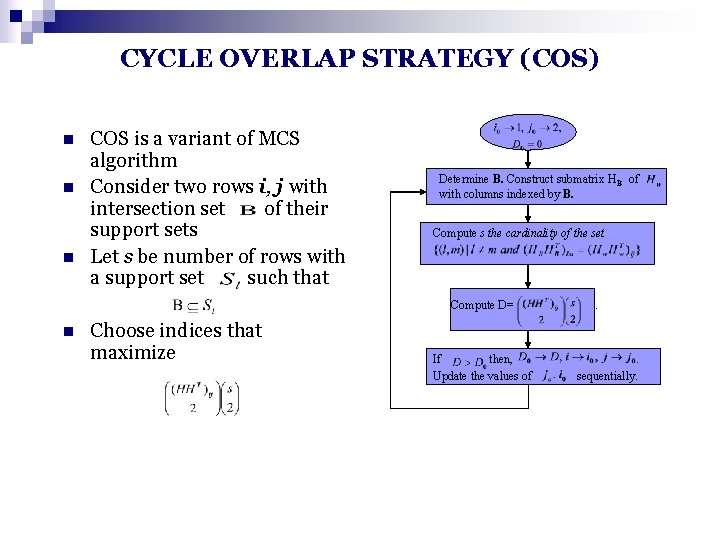
CYCLE OVERLAP STRATEGY (COS) n n n COS is a variant of MCS algorithm Consider two rows i, j with intersection set of their support sets Let s be number of rows with a support set such that Determine B. Construct submatrix HB of with columns indexed by B. Compute s the cardinality of the set Compute D= n Choose indices that maximize If then, Update the values of . . sequentially.

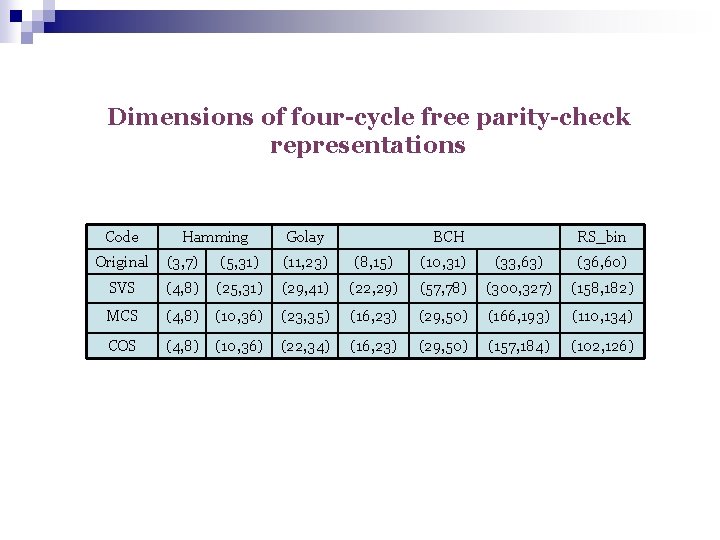
Dimensions of four-cycle free parity-check representations Code Hamming Golay BCH RS_bin Original (3, 7) (5, 31) (11, 23) (8, 15) (10, 31) (33, 63) (36, 60) SVS (4, 8) (25, 31) (29, 41) (22, 29) (57, 78) (300, 327) (158, 182) MCS (4, 8) (10, 36) (23, 35) (16, 23) (29, 50) (166, 193) (110, 134) COS (4, 8) (10, 36) (22, 34) (16, 23) (29, 50) (157, 184) (102, 126)

EXTENSION: CODES OVER NON-BINARY FIELDS n Motivation Applications to Reed-Solomon (RS) codes Ø Two Approaches: Ø Ø Binary image mapping: Kumar, Milenkovic, Vasic CTW 2004, Milenkovic, Kumar ISIT 2004 Choice of matrix field representation and primitive polynomial, initial choice of parity-check matrix followed by cycle elimination for the binary parity-check matrix Ø Direct cycle elimination followed by vector message passing

DIRECT CYCLE ELIMINATION n n Define two types of cycles Type 1 cycle: If n n n are the values taken by the three variable nodes in R CF then, Type 2 cycle: are the values taken by the three variable nodes in RCF then, Type 2 cycle elimination introduces six-cycle while eliminating four-cycle Number of Type-1 cycles: Number of Type-2 cycles:

ALGEBRAIC CODES AND UNEQUAL ERROR PROTECTION BASED ON ITERATIVE DECODING Ø Codes which provide UEP: practical applications for n n Non-uniform channels Joint coding for parallel channels Image transmission over wireless channels Page oriented optical memories Ø Fekri 2002 – LDPC codes for UEP based on optimizing degree distributions No guarantee/tuning possibility for degree of protection Ø Dumer 2000 - Decoding algorithm for RM codes based on their Plotkin-type structure n n Decodes different parts of the codeword separately Inherently achieves UEP for different portions of the codeword

PLOTKIN CONSTRUCTION Ø Parity-check matrix of Depth-1 Plotkin-type code: C = {|u|u+v |; u in C 1; v in C 2 } Ø Global iterative decoder not a good option: H 2 placed side by side, introduces at least four-cycles Ø The UEP obtained for Plotkin-type codes is an inherent characteristic of the proposed decoding algorithm Ø As in other UEP schemes involving LDPC codes, one can vaguely associate the UEP obtained here to the different degree distributions Ø Encoding: Individual for all different component codes

INTUITION n n n |u|u+v|: Have “two copies” of u Only one copy of v, which is implicit ADVANTAGES OF THE SCHEME: n n Reduced-complexity encoding Low-complexity soft-output decoders Flexibility of UEP code construction, levels of UEP error protection and adaptability to channel conditions Excellent performance for best protected components

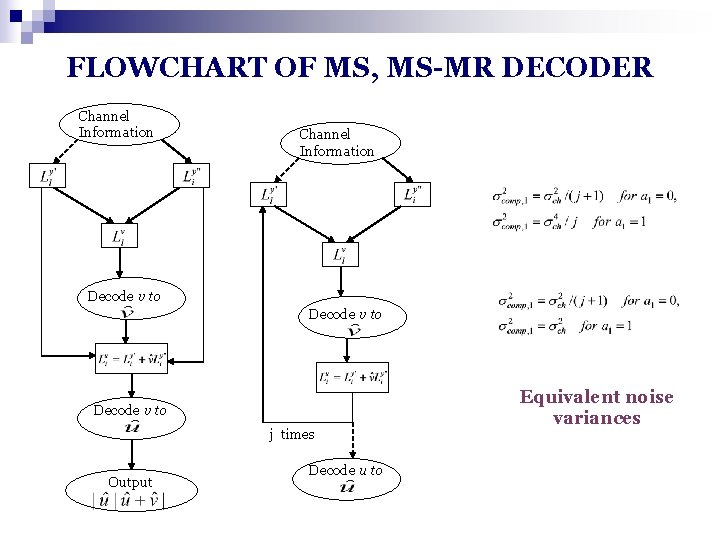
MS Multi-Stage TMS Threshold Multi-Stage MR-MS Multi-Round Multi-Stage Kumar, Milenkovic Globecom 2004, TCOMM 2004

FLOWCHART OF MS, MS-MR DECODER Channel Information Decode v to j times Output Decode u to Equivalent noise variances

THANK YOU!