The Role of Specialization in LDPC Codes Jeremy

The Role of Specialization in LDPC Codes Jeremy Thorpe Pizza Meeting Talk 2/12/03

Talk Overview w LDPC Codes w Message Passing Decoding w Analysis of Message Passing Decoding (Density Evolution) w Approximations to Density Evolution w Design of LDPC Codes using D. E.

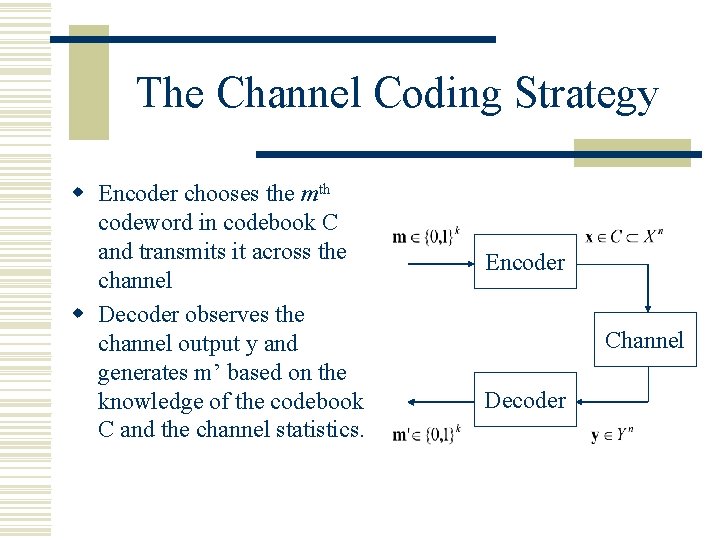
The Channel Coding Strategy w Encoder chooses the mth codeword in codebook C and transmits it across the channel w Decoder observes the channel output y and generates m’ based on the knowledge of the codebook C and the channel statistics. Encoder Channel Decoder

Linear Codes w A linear code C (over a finite field) can be defined in terms of either a generator matrix or parity-check matrix. w Generator matrix G (k×n) w Parity-check matrix H (n-k×n)

LDPC Codes w LDPC Codes -- linear codes defined in terms of H. w H has a small average number of non-zero elements per row

Graph Representation of LDPC Codes w H is represented by a Variable nodes bipartite graph. w There is an edge from v to c if and only if: . . . w A codeword is an assignment of v's s. t. : Check nodes

Regular (λ, ρ) LDPC codes . . . w Every variable node Variable nodes has degree λ, every check node has degree ρ. w Ensemble is defined by π matching left edge "stubs" with right edge "stubs via a random Check nodes permutation

Message-Passing Decoding of LDPC Codes w Message Passing (or Belief Propagation) decoding is a low-complexity algorithm which approximately answers the question “what is the most likely x given y? ” w MP recursively defines messages mv, c(i) and mc, v(i) from each node variable node v to each adjacent check node c, for iteration i=0, 1, . . .

Two Types of Messages. . . w Liklihood Ratio w Probability Difference w For y 1, . . . yn independent w For x 1, . . . xn conditionally on x: independent:

. . . Related by the Biliniear Transform w Definition: w Properties:

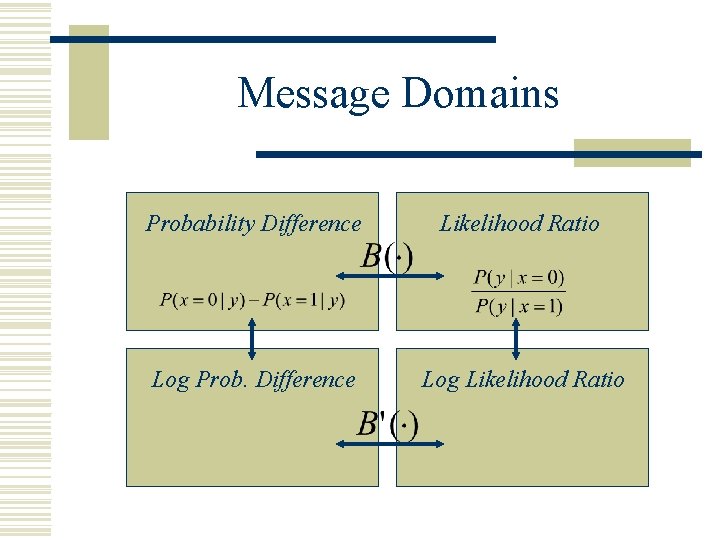
Message Domains Probability Difference Likelihood Ratio Log Prob. Difference Log Likelihood Ratio

Variable to Check Messages w On any iteration i, the message from v to c is: v c. . . w It is computed like:

Check to Variable Messages w On any iteration, the message from c to v is: v c w It is computed like: . . . w Assumption: Incoming messages are indep.

Decision Rule w After sufficiently many iterations, return the likelihood ratio:

Theorem about MP Algorithm r . . . v . . . w If the algorithm stops after r iterations, then the algorithm returns the maximum a posteriori probability estimate of xv given y within radius r of v. w However, the variables within a radius r of v must be dependent only by the equations within radius r of v, . . .

Analysis of Message Passing Decoding (Density Evolution) w in Density Evolution we keep track of message densities, rather than the densities themselves. w At each iteration, we average over all of the edges which are connected by a permutation. w We assume that the all-zeros codeword was transmitted (which requires that the channel be symmetric).

D. E. Update Rule w The update rule for Density Evolution is defined in the additive domain of each type of node. w Whereas in B. P, we add (log) messages: w In D. E, we convolve message densities:

Familiar Example: w If one die has density function given by: 1 2 3 4 5 6 w The density function for the sum of two dice is given by the convolution: 2 3 4 5 6 7 8 9 10 1112

D. E. Threshold w Fixing the channel message densities, the message densities will either "converge" to minus infinity, or they won't. w For the gaussian channel, the smallest (infimum) SNR for which the densities converge is called the density evolution threshold.

Regular (λ, ρ) LDPC codes w Every variable node has degree λ, every check node has degree ρ. w Best rate 1/2 code is (3, 6), with threshold 1. 09 d. B. w This code had been invented by 1962 by Robert Gallager.

D. E. Simulation of (3, 6) codes w Set SNR to 1. 12 d. B (. 03 above threshold) w Watch fraction of "erroneous messages" from check to variable. w (note that this fraction does not characterize the distribution fully)

Improvement vs. current error fraction for Regular (3, 6) w Improvement per iteration is plotted against current error fraction. w Note there is a single bottleneck which took most of the decoding iterations.

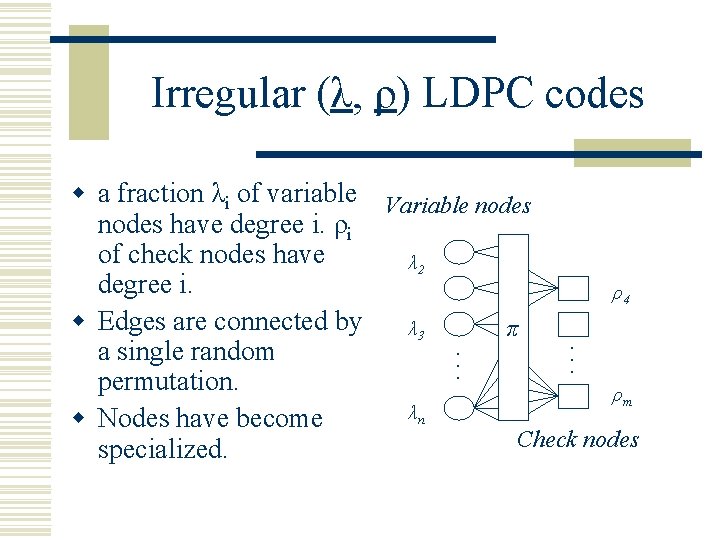
Irregular (λ, ρ) LDPC codes . . . w a fraction λi of variable Variable nodes have degree i. ρi of check nodes have λ 2 degree i. ρ4 w Edges are connected by λ 3 π a single random permutation. ρm λn w Nodes have become Check nodes specialized.

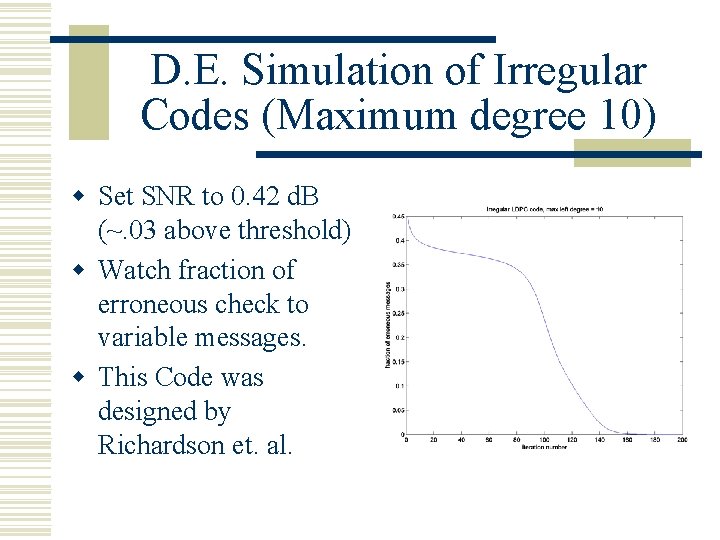
D. E. Simulation of Irregular Codes (Maximum degree 10) w Set SNR to 0. 42 d. B (~. 03 above threshold) w Watch fraction of erroneous check to variable messages. w This Code was designed by Richardson et. al.

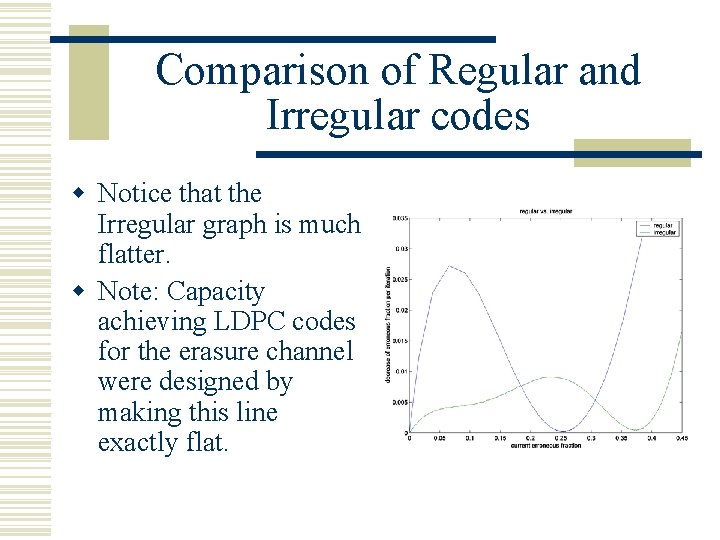
Comparison of Regular and Irregular codes w Notice that the Irregular graph is much flatter. w Note: Capacity achieving LDPC codes for the erasure channel were designed by making this line exactly flat.

Multi-edge-type construction w Edges of a particular "color" are connected through a permutation. w Edges become specialized. Each edge type has a different message distribution each iteration.

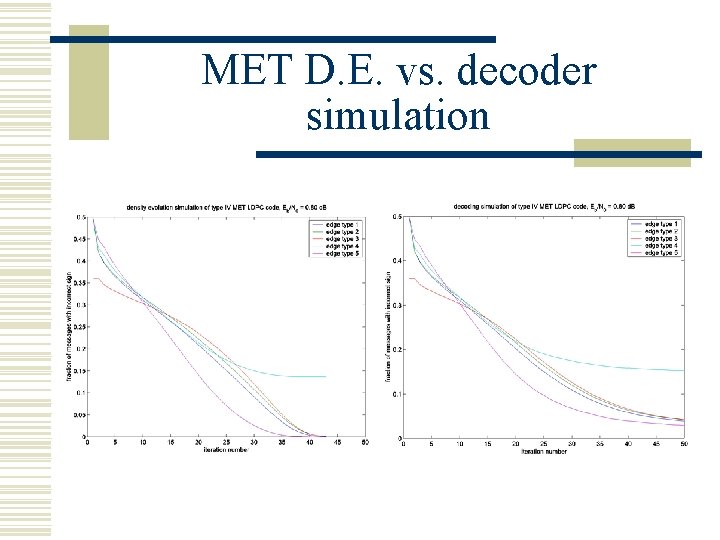
D. E. of MET codes. w For Multi-edge-type codes, Density evolution tracks the density of each type of message separately. w Comparison was made to real decoding, next slide (courtesy of Ken Andrews).

MET D. E. vs. decoder simulation

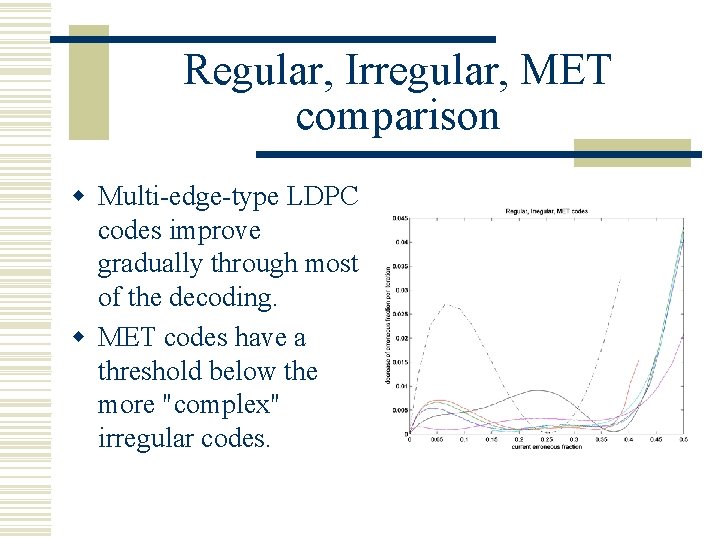
Regular, Irregular, MET comparison w Multi-edge-type LDPC codes improve gradually through most of the decoding. w MET codes have a threshold below the more "complex" irregular codes.

Design of Codes using D. E. w Density evolution provides a moderately fast way to evaluate single- and multi- edge type degree distributions (hypothesis-testing). w Much faster approximations to Density Evolution can easily be put into an outer loop which performs function minimization. w Semi-Analytic techniques exist as well.

Review w Iterative Message Passing can be used to decode LDPC codes. w Density Evolution can be used to predict the performance of MP for infinitely large codes. w More sophisticated classes of codes can be designed to close the gap to the Shannon limit.

Beyond MET Codes (future work) w Traditional LDPC codes are designed in two stages: design of the degree distribution and design of the specific graph. w Using very fast and accurate approximations to density evolution, we can evaluate the effect of placing or removing a single edge in the graph. w Using an evolutionary algorithm like Simulated Annealing, we can optimize the graph directly, changing the degree profile as needed.