Hasil Kali Skalar Dua Vektor 1 Setelah menyaksikan









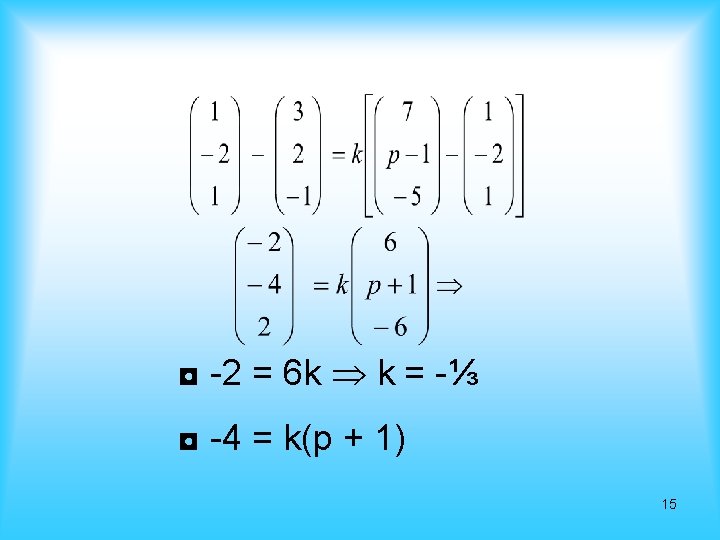























- Slides: 41

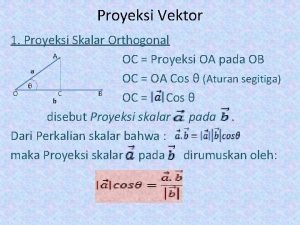
Hasil Kali Skalar Dua Vektor 1

Setelah menyaksikan tayangan ini Anda dapat Menggunakan rumus Perbandingan vektor, menentukan hasil kali skalar dua vektor & sudut antara dua vektor 2

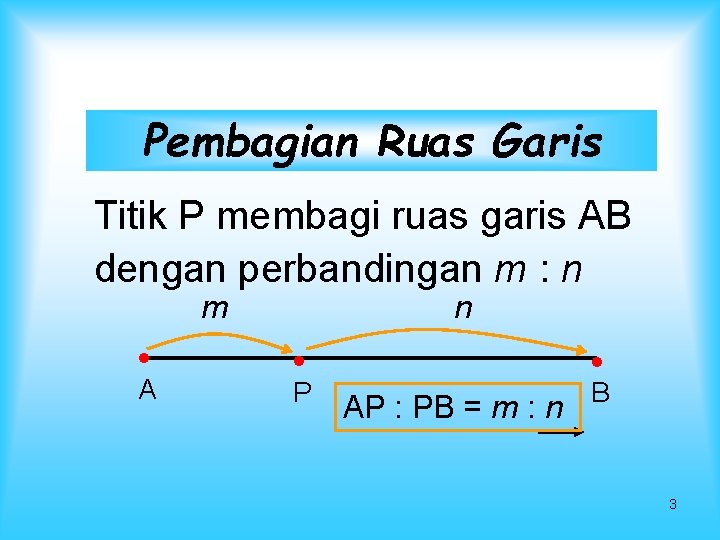
Pembagian Ruas Garis Titik P membagi ruas garis AB dengan perbandingan m : n m A n P AP : PB = m : n B 3

• Bila P di dalam AB, maka AP dan • PB mempunyai arah yang sama, • sehingga m dan n tandanya sama 4

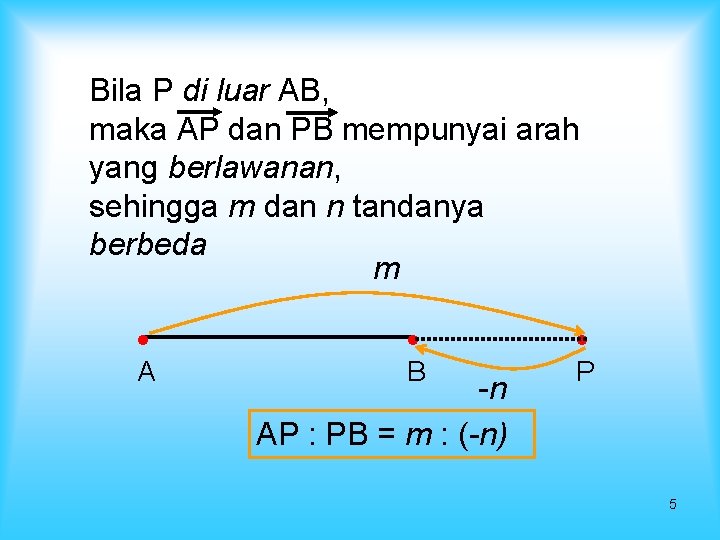
Bila P di luar AB, maka AP dan PB mempunyai arah yang berlawanan, sehingga m dan n tandanya berbeda m A B -n AP : PB = m : (-n) P 5

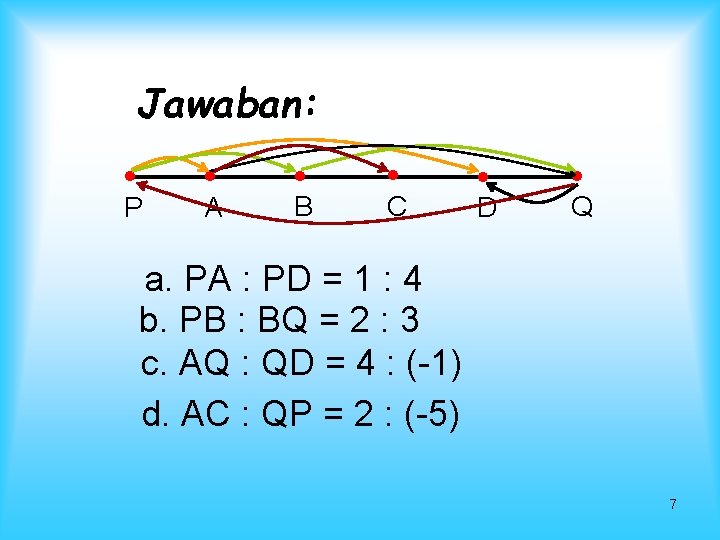
Contoh : Ruas garis PQ dibagi menjadi lima bagian yang sama oleh titik-titik A, B, C, dan D. Hitunglah nilai-nilai perbandingan a. PA : PD b. PB : BQ c. AQ : QD d. AC : QP 6

Jawaban: P A B C D Q a. PA : PD = 1 : 4 b. PB : BQ = 2 : 3 c. AQ : QD = 4 : (-1) d. AC : QP = 2 : (-5) 7

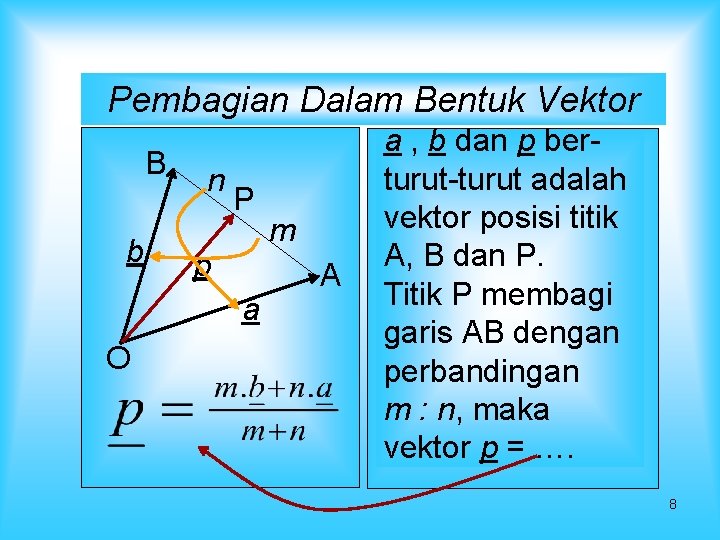
Pembagian Dalam Bentuk Vektor B b n P p a O m A a , b dan p berturut-turut adalah vektor posisi titik A, B dan P. Titik P membagi garis AB dengan perbandingan m : n, maka vektor p = …. 8

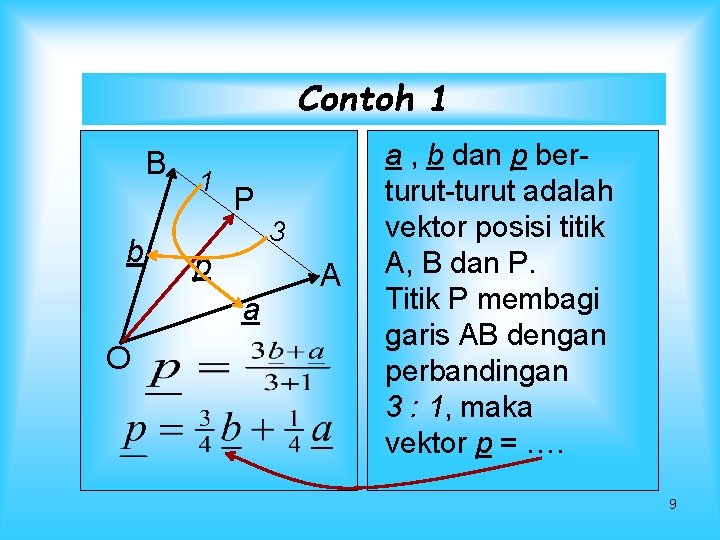
Contoh 1 B b 1 P p a O 3 A a , b dan p berturut-turut adalah vektor posisi titik A, B dan P. Titik P membagi garis AB dengan perbandingan 3 : 1, maka vektor p = …. 9

Contoh 2 Titik P membagi ruas garis AB di luar dengan perbandingan AP : PB = 9 : 4 Jika titik A(4, 3, 1) dan B(-6, 8, 1), maka koordinat titik P adalah…. Jawab: AP : PB = 9 : (-4), karena P di luar AB maka 10

Jadi titik P adalah (-14, 12, 1) 11

Contoh 3 P adalah titik (-1, 1, 3), Q adalah (2, 0, 1) dan R adalah(-7, 3, 7). Tunjukan bahwa P, Q dan R segaris (kolinear), dan Tentukan perbandingan dari PQ : QR Jawab: PQ = q – p = QR = r – q = 12

PQ = q – p = QR = r – q = QR = 3 PQ, terbukti P, Q dan R segaris dengan perbandingan PQ : QR = 1 : 3 13

Contoh 4 Titik A(3, 2, -1), B(1, -2, 1) dan C(7, p -1, -5) segaris untuk nilai p =…. Jawab: Segaris: AB = k. BC b – c = k(c – b) 14
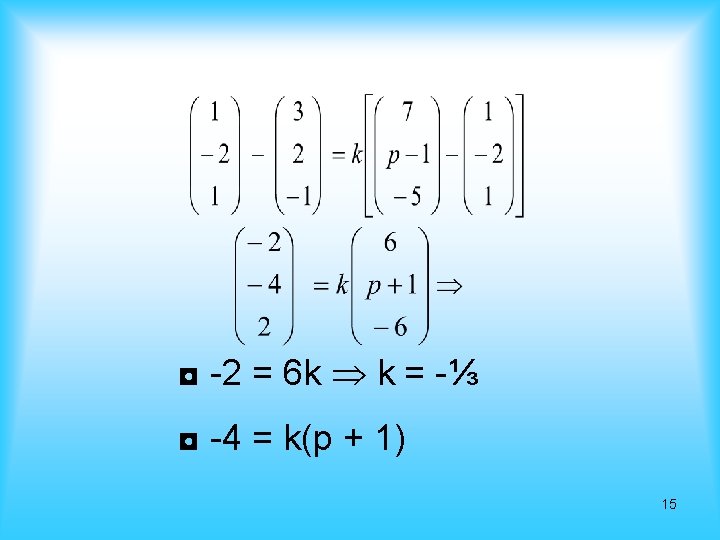

◘ -4 = k(p + 1) -4 = - ⅓(p + 1), ruas kiri & kanan di kali -3 12 = p + 1 Jadi p = 11 16

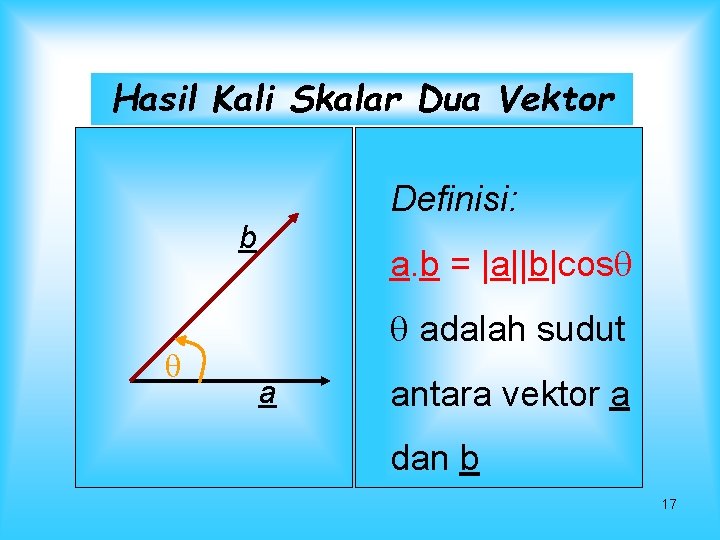
Hasil Kali Skalar Dua Vektor Definisi: b a. b = |a||b|cos adalah sudut a antara vektor a dan b 17

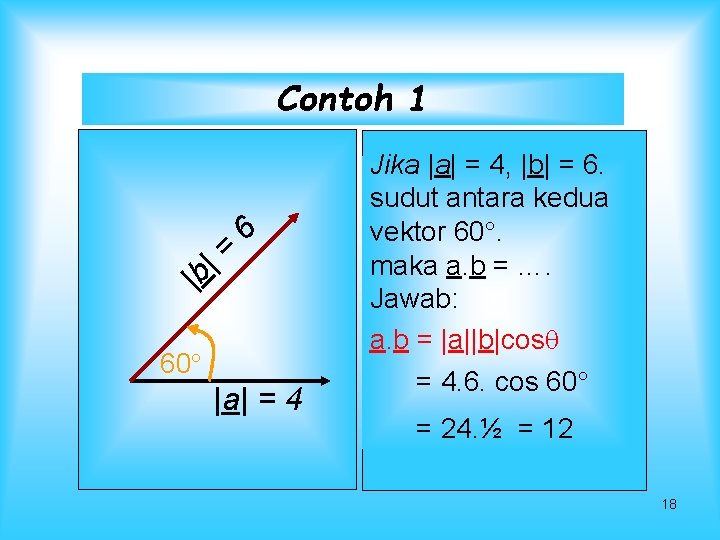
Contoh 1 | = | b 6 60 |a| = 4 Jika |a| = 4, |b| = 6. sudut antara kedua vektor 60. maka a. b = …. Jawab: a. b = |a||b|cos = 4. 6. cos 60 = 24. ½ = 12 18

Contoh 2 |b| = 2 |a| = 5 Jika |a| = 5, |b| = 2. sudut antara kedua vektor 90. maka a. b = …. Jawab: a. b = |a||b|cos = 5. 2. cos 90 = 10. 0 = 0 19

Jika a = a 1 i +a 2 j + a 3 k dan b = b 1 i + b 2 j +b 3 k maka Hasil Kali Skalar Dua Vektor dirumuskan dengan a. b =a 1 b 1 + a 2 b 2 + a 3 b 3 20

Contoh 1 Jika a = 2 i + 3 j + k dan b = 5 i -j + 4 k maka hasil kali skalar a. b =. . Jawab: a. b = a 1 b 1 + a 2 b 2 + a 3 b 3 = 2. 5 + 3. (-1) + 1. 4 = 10 – 3 + 4 = 11 21

Contoh 2 Jika a = 2 i + 3 j + k dan b = 5 i -j + 4 k maka hasil kali skalar b. a =. . Jawab: b. a = b 1 a 1 + b 2 a 2 + b 3 a 3 = 5. 2 + (-1). 3 + 4. 1 = 10 – 3 + 4 = 11 22

Sifat-sifat Perkalian Skalar üa. b = b. a ük(a. b) = ka. b = kb. a üa. a = |a|² üa. (b ± c) = a. b ± a. c üa. b = 0 jika dan hanya jika a b 23

Contoh 1 Jika a = -2 i + 3 j + 5 k , b = 3 i -5 j + 4 k dan c = -7 j + k maka a(b – c) =. . Jawab: a. (b – c) = a. b – a. c a. b = (-2)3 + 3(-5) + 5. 4 = -6 – 15 + 20 = -1 24


Contoh 2 Jika vektor a dan b membentuk sudut 60 , |a| = 4, dan |b| = 3, maka a. (a + b) = …. Jawab: a. (a + b) = a. a + a. b = |a|² + |a|. |b| cos 60 = 16 + 12. ½ = 16 + 6 = 22 26

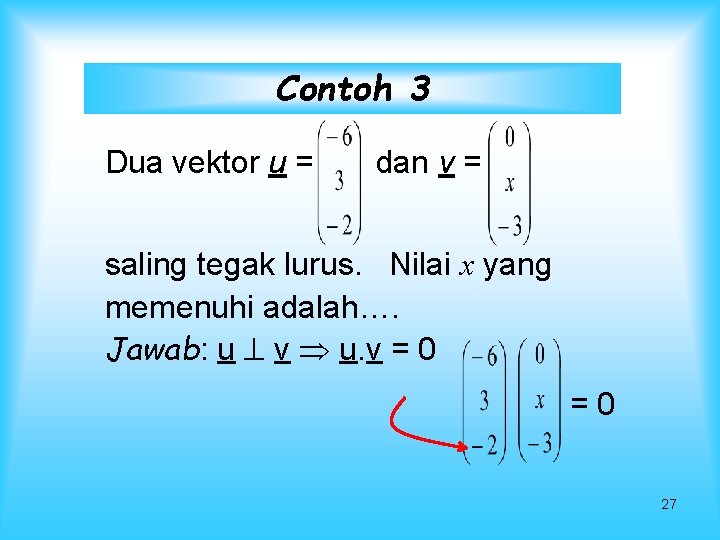
Contoh 3 Dua vektor u = dan v = saling tegak lurus. Nilai x yang memenuhi adalah…. Jawab: u v u. v = 0 =0 27

u v u. v = 0 =0 (-6). 0 + 3. x + (-2)(-3) = 0 0 + 3 x + 6 = 0 3 x = -6. Jadi x = -2 28

Contoh 4 Dua vektor a = dan b = dan vektor (a + m. b) tegak lurus. vektor a. Nilai m adalah…. Jawab: (a + mb) a (a + mb). a = 0 29


Dengan rumus hasil kali skalar dua vektor, kita dapat menentukan besar sudut antara dua vektor. Dari a. b = |a||b|cos , kita peroleh 31

Contoh 1 Tentukan besar sudut antara vektor a = 2 i + j - 2 k dan vektor b = -j + k Jawab: 32

cos = -½ 2 Jadi = 135 33

Contoh 2 Diketahui titik-titik A(3, 2, 4), B(5, 1, 5) dan C(4, 3, 6). AB wakil dari u dan AC wakil dari v. Kosinus sudut yang dibentuk oleh vektor u dan v adalah…. Jawab: misal sudut antara u dan v adalah 34

u = AB = b – a = v = AC = c – a = cos (u, v) = 35

Jadi kosinus sudut antara u dan v = ½ 36

Contoh 3 Diketahui |a|=2 ; |b|=3, dan b. (a + b) =12. Besar sudut antara vektor a dan b adalah…. Jawab: b. (a + b) =12 b. a + b. b = 12 |b|. |a| cos (a, b) + |b|² = 12 3. 2. cos (a, b) + 3² = 12 37

3. 2. cos (a, b) + 3² = 12 6. cos (a, b) + 9 = 12 6. cos (a, b) = 12 – 9 6. cos (a, b) = 3 cos (a, b) = ½ (a, b) = 60 Jadi besar sudut antara a dan b adalah 60 38

Contoh 4 Diketahui |a|= 6; (a –b)(a + b) =0 a. (a – b) =3. Besar sudut antara vektor a dan b adalah…. Jawab: (a – b)(a + b) = 0 a. a + a. b – b. a – b. b = 0 |a|² - |b|² = 0 → |a|² = |b|² → |a| = |b| = 6 39

a. (a – b) = 3 a. a + a. b = 3 |a|² + |b|. |a| cos (a, b)= 3 6 + 6. 6. cos (a, b) = 3 6 - 6. cos (a, b) = 3 40

6 - 6. cos (a, b) = 3 – 6 - 6. cos (a, b) = -3 cos (a, b) = ½ → (a, b) = ⅓π Jadi besar sudut antara vektor a dan vektor b adalah ⅓π 41
 Hasil kali skalar antara dua vektor
Hasil kali skalar antara dua vektor Hasil kali skalar dua vektor
Hasil kali skalar dua vektor Hasil kali silang vektor
Hasil kali silang vektor Rumus vektor tegak lurus
Rumus vektor tegak lurus Turunan parsial vektor
Turunan parsial vektor Diketahui vektor-vektor sebagai berikut gambarlah vektor
Diketahui vektor-vektor sebagai berikut gambarlah vektor Hasil kali titik
Hasil kali titik Ruang hasil kali dalam
Ruang hasil kali dalam Kelajuan besaran skalar atau vektor
Kelajuan besaran skalar atau vektor Vektor
Vektor Contoh soal panjang proyeksi vektor
Contoh soal panjang proyeksi vektor Wektor a skalar
Wektor a skalar Perkalian dot vektor
Perkalian dot vektor Vektor keresztszorzat
Vektor keresztszorzat Yang termasuk besaran skalar
Yang termasuk besaran skalar Perkalian vektor
Perkalian vektor Vektor
Vektor Maksud penyakit bawaan vektor
Maksud penyakit bawaan vektor Vektor proyeksi
Vektor proyeksi Ciri ciri kubus
Ciri ciri kubus Vektor vektor ekuivalen pada sistem koordinat kartesius
Vektor vektor ekuivalen pada sistem koordinat kartesius Notasi notasi vektor
Notasi notasi vektor Jika vektor v=xi+yj-zk panjang vektor v adalah
Jika vektor v=xi+yj-zk panjang vektor v adalah Paralelogramma fogalma
Paralelogramma fogalma Mengevaluasi penggabungan gambar vektor dan bitmap (raster)
Mengevaluasi penggabungan gambar vektor dan bitmap (raster) Dua tahun yang lalu umur harry 6 kali umur laras
Dua tahun yang lalu umur harry 6 kali umur laras Sepuluh tahun yang lalu umur ita dua kali umur tika
Sepuluh tahun yang lalu umur ita dua kali umur tika Mobil pertama bermassa dua kali
Mobil pertama bermassa dua kali Hasil tes matematika 14 siswa sebagai berikut 4 5 5
Hasil tes matematika 14 siswa sebagai berikut 4 5 5 Jumlah dan hasil kali akar akar persamaan kuadrat
Jumlah dan hasil kali akar akar persamaan kuadrat Contoh soal ortonormal
Contoh soal ortonormal Hasil kali bilangan cacah berselisih 5 adalah 84
Hasil kali bilangan cacah berselisih 5 adalah 84 Contoh proses gram schmidt
Contoh proses gram schmidt Hasil kali kelarutan
Hasil kali kelarutan Harga 3 lusin pensil adalah rp45.000 harga 32 pensil adalah
Harga 3 lusin pensil adalah rp45.000 harga 32 pensil adalah Contoh ruang hasil kali dalam
Contoh ruang hasil kali dalam Axb vektor
Axb vektor Kesamaan dua vektor
Kesamaan dua vektor Panjang vektor
Panjang vektor Kesimpulan pengolahan hasil belajar
Kesimpulan pengolahan hasil belajar Skalár obyčajný
Skalár obyčajný Skalar adalah
Skalar adalah