Wektory i skalary Skalar wielko fizyczna ktr mona

Wektory i skalary -Skalar – wielkość fizyczna, którą można przedstawić za pomocą liczby (np. objętość, temperatura) - Wektor – wielkość fizyczna, która ma długość („wielkość”), kierunek i zwrot (np. siła, przemieszczenie) zwrot kierunek długość (moduł, wartość bezwzględna)

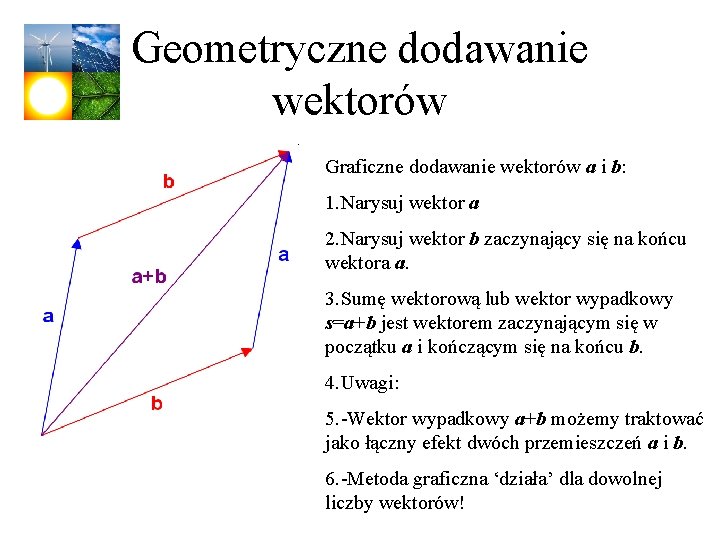
Geometryczne dodawanie wektorów Graficzne dodawanie wektorów a i b: 1. Narysuj wektor a 2. Narysuj wektor b zaczynający się na końcu wektora a. 3. Sumę wektorową lub wektor wypadkowy s=a+b jest wektorem zaczynającym się w początku a i kończącym się na końcu b. 4. Uwagi: 5. -Wektor wypadkowy a+b możemy traktować jako łączny efekt dwóch przemieszczeń a i b. 6. -Metoda graficzna ‘działa’ dla dowolnej liczby wektorów!

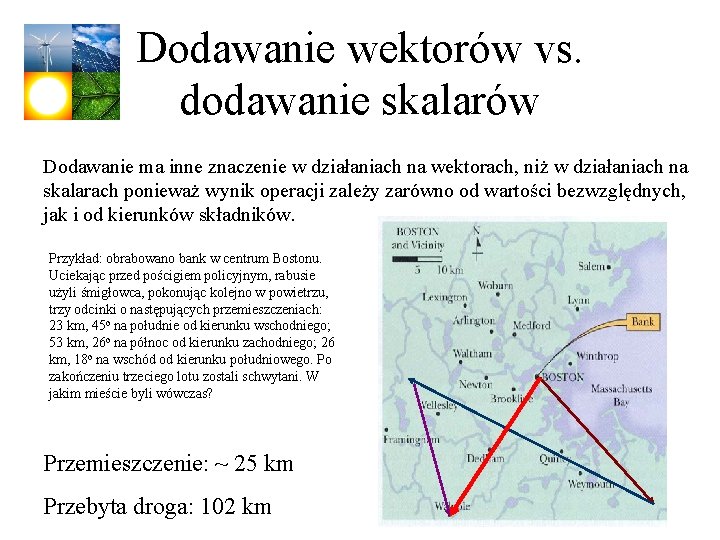
Dodawanie wektorów vs. dodawanie skalarów Dodawanie ma inne znaczenie w działaniach na wektorach, niż w działaniach na skalarach ponieważ wynik operacji zależy zarówno od wartości bezwzględnych, jak i od kierunków składników. Przykład: obrabowano bank w centrum Bostonu. Uciekając przed pościgiem policyjnym, rabusie użyli śmigłowca, pokonując kolejno w powietrzu, trzy odcinki o następujących przemieszczeniach: 23 km, 45 o na południe od kierunku wschodniego; 53 km, 26 o na północ od kierunku zachodniego; 26 km, 18 o na wschód od kierunku południowego. Po zakończeniu trzeciego lotu zostali schwytani. W jakim mieście byli wówczas? Przemieszczenie: ~ 25 km Przebyta droga: 102 km

Wektory jednostkowe Wektorem jednostkowym nazywamy wektor o długości 1, skierowany w określonym kierunku. W kartezjańskim układzie współrzędnych, wektory jednostkowe dodatnich kierunków osi x, y, z oznaczamy i, j, k.

Wektory jednostkowe Wektorów jednostkowych możemy używać do zapisu innych wektorów. y F yj F F xi x F = Fxi + Fyj + Fzk Fxi, Fyj, Fzk – wektory składowe wektora F

Dodawanie wektorów na składowych Inna metodą dodawania wektorów jest dodawanie ich składowych dla każdej osi. r=a+b rx = ax + bx ry = a y + b y rz = az + bz 1. Rozkładamy wektory na składowe 2. Dodajemy do siebie składowe wektorów dla każdej osi 3. Wyznaczamy wektorową sumę na podstawie sumy składowych

Rozkładanie wektorów na składowe y F yj F q F xi x Fx = Fcosq oraz Fy = Fsinq

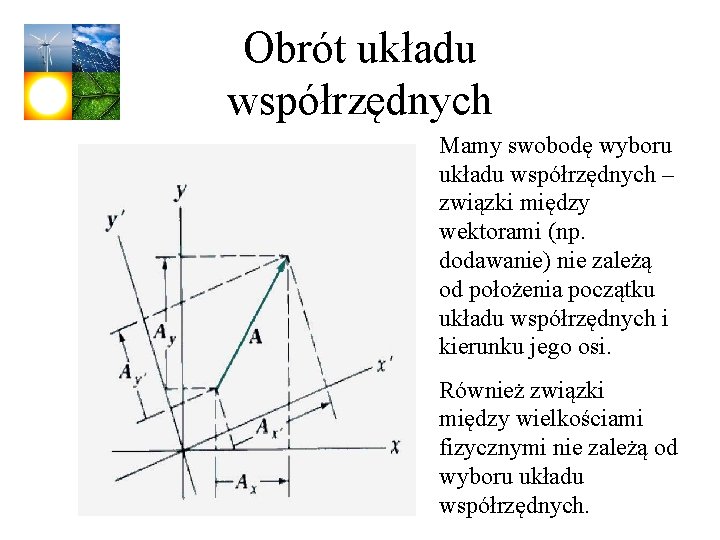
Obrót układu współrzędnych Mamy swobodę wyboru układu współrzędnych – związki między wektorami (np. dodawanie) nie zależą od położenia początku układu współrzędnych i kierunku jego osi. Również związki między wielkościami fizycznymi nie zależą od wyboru układu współrzędnych.

Wektory a prawa fizyki Prawa fizyki w układzie przesuniętym (translacja) i obróconym są takie same. Nazywa się to symetrią praw fizyki względem translacji i obrotów. A odbicie lustrzane?

Lustrzane łamanie symetrii - Odbicie przestrzenne, odbicie P, odbicie lustrzane – zmiana znaku wszystkich współrzędnych przestrzennych. - Odbicie czasowe, odbicie T – zmiana znaku wszystkich współrzędnych czasowych. - Odbicie ładunkowe, odbicie C, zmiana znaku wszystkich ładunków elektrycznych. Istnieją przykłady łamania symetrii P, T i C – w lustrzanym odbiciu Wszechświata obowiązują inne prawa fizyki.

Mnożenie wektorów Mnożenie wektora przez skalar b = s*a - b = s*a – długość b wynosi s razy długość a - kierunek a i b jest taki sam - zwrot b jest zgodny ze zwrotem a, jeśli s jest dodatnie, a przeciwny, gdy s jest ujemne. Mnożenie wektora przez wektor Istnieją dwa sposoby mnożenia wektora przez wektor: -iloczyn skalarny -iloczyn wektorowy

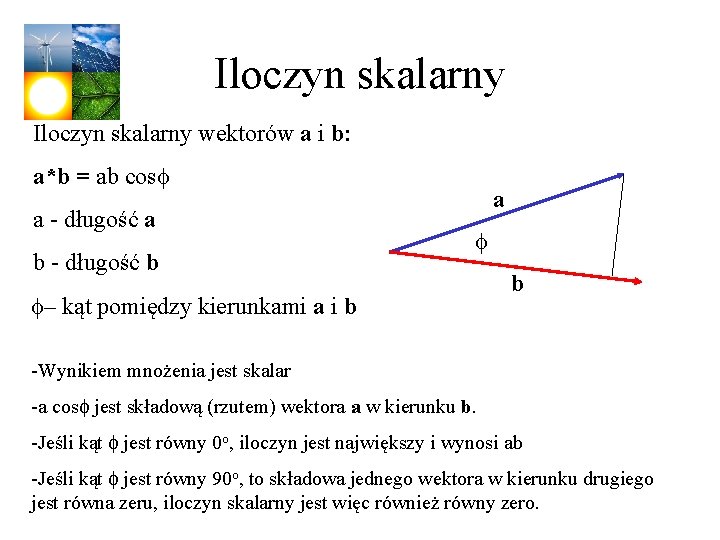
Iloczyn skalarny wektorów a i b: a*b = ab cosf a - długość a b - długość b a f f– kąt pomiędzy kierunkami a i b b -Wynikiem mnożenia jest skalar -a cosf jest składową (rzutem) wektora a w kierunku b. -Jeśli kąt f jest równy 0 o, iloczyn jest największy i wynosi ab -Jeśli kąt f jest równy 90 o, to składowa jednego wektora w kierunku drugiego jest równa zeru, iloczyn skalarny jest więc również równy zero.

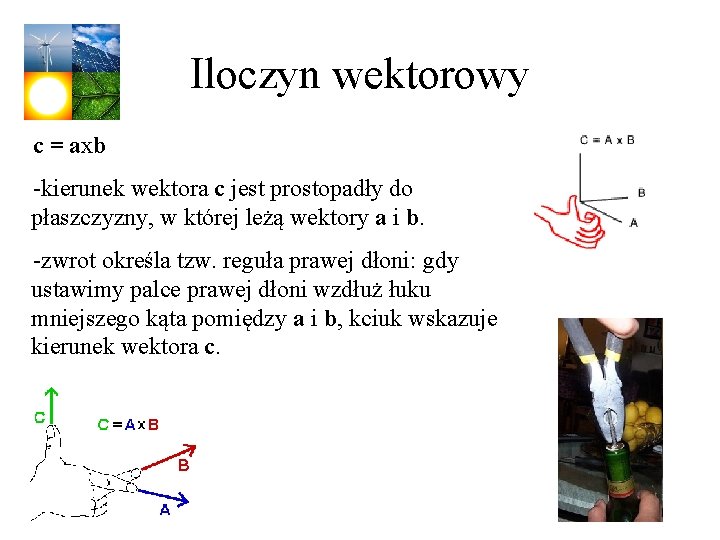
Iloczyn wektorowy wektorów a i b: c = axb c = ab sinf – długość wektora c a f b f – mniejszy z kątów pomiędzy kierunkami a i b -Wynikiem mnożenia jest wektor -Jeśli kąt f jest równy 0 o, iloczyn wynosi zero -Jeśli kąt f jest równy 90 o, to iloczyn jest największy i wynosi ab

Iloczyn wektorowy c = axb -kierunek wektora c jest prostopadły do płaszczyzny, w której leżą wektory a i b. -zwrot określa tzw. reguła prawej dłoni: gdy ustawimy palce prawej dłoni wzdłuż łuku mniejszego kąta pomiędzy a i b, kciuk wskazuje kierunek wektora c.

Wektory - powtórzenie

Ruch – zmiana położenia obiektu w czasie Świat jest w ciągłym ruchu Dział fizyki zajmujący się opisem ruchu – kinematyka (z greckiego kinēma - ruch) Dzisiaj: -ruch wzdłuż linii prostej -poruszające ciało jest obiektem punktowym

Położenie i przemieszczenie Położenie ciała wyznaczamy względem pewnego punktu odniesienia np. początku osi x. Np. x = 5 m -3 -2 -1 0 1 2 3 4 5 6 x [m] Zmianę położenie ciała od punktu x 1 do punktu x 2 nazywamy przemieszczeniem Dx: Dx = x 2 - x 1

Prędkość średnia i chwilowa Jedną z możliwości opisu ruchu jest podanie średniej prędkości: vsr = Dx/ Dt vsr jest stosunkiem przemieszczenia cząstki Dx w pewnym przedziale czasu, do wielkości tego przedziału czasu Dt. Gdy chcemy znać prędkości cząstki w danej chwili, musimy podać prędkość chwilową: Wyrażenie oznacza, że zmniejszamy przedział czasu do zera Wyrażenie oznacza pochodną x względem t

Przyśpieszenie Gdy prędkość cząstki się zmienia, doznaje ona przyśpieszenia. Przyśpieszenie średnie: asr = Dv/ Dt http: //en. wikipedia. org/wiki/List_of_fastest_cars_by_acceleration

Przyśpieszenie chwilowe: Słowami: przyśpieszenie cząstki w danej chwili jest równe szybkości zmiany prędkości cząstki w danej chwili. Możemy zapisać: Przyśpieszenie cząstki w danej chwili jest równe drugiej pochodnej jej położenia x względem czasu t.

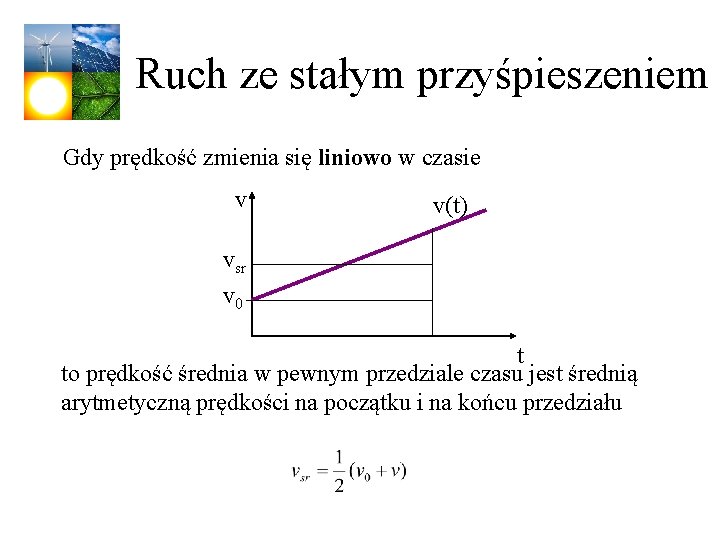
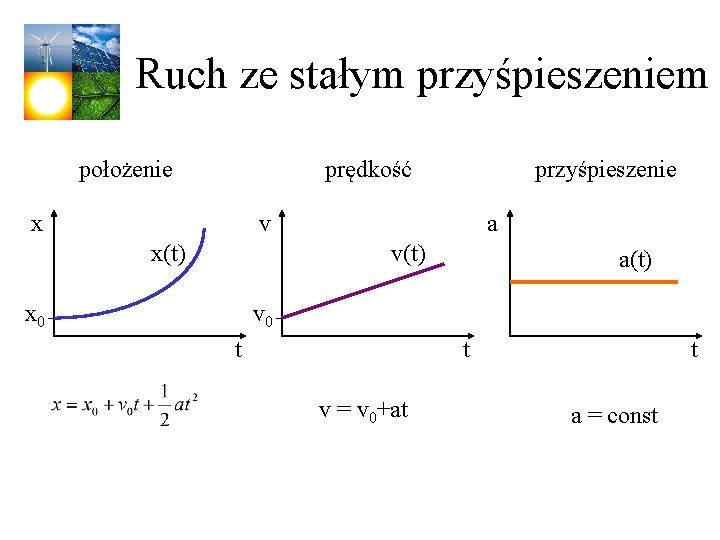
Ruch ze stałym przyśpieszeniem Gdy przyśpieszenie jest stałe, przyśpieszenie średnie jest równe przyśpieszeniu chwilowemu: v 0 – prędkość cząstki w chwili t = 0. Przekształcając: v = v 0+at Oznacza to, że prędkość zmienia się liniowo w czasie. W podobny sposób przekształcamy równanie na vsr: x = x 0+vsrt

Ruch ze stałym przyśpieszeniem Gdy prędkość zmienia się liniowo w czasie v v(t) vsr v 0 t to prędkość średnia w pewnym przedziale czasu jest średnią arytmetyczną prędkości na początku i na końcu przedziału

Ruch ze stałym przyśpieszeniem Podstawiając v = v 0+at Dostajemy: Wstawiając do x = x 0+vsrt Dostajemy: albo:

Ruch ze stałym przyśpieszeniem położenie prędkość x przyśpieszenie v x(t) a v(t) x 0 a(t) v 0 t t v = v 0+at t a = const

Spadek swobodny Ciało umieszczone w ziemskim polu grawitacyjnym doznaje przyśpieszenia o stałej wartości, skierowanego w dół. Przyśpieszenie to nazywa się przyśpieszeniem ziemskim i oznacza g. Przyjmujemy wartość g = 9. 8 m/s 2 Spadek swobodny opisują równania ruchu ze stałym przyśpieszeniem (o ile wpływ powietrza na ruch można pominąć).

Spadek swobodny - przykład W 1989, Peter Debernardi (42) i Jeffrey (Clyde) Petkovich (25) zostali pierwszą drużyną, która spłynęła wodospadem Niagara o wysokości 48 m, w stalowej kapsule. Jak długo spadali i z jaką prędkością uderzyli w spienione wody na dole? -48 = 0 + 0 – 0. 5*9. 8*t 2 = 48/4. 9 [m/m/s 2] t = 3. 1 s v = v 0+at v = -9. 8*3. 1[(m/s 2)*s] = -31 m/s ~ 110 km/h