PERTANYAAN DARI SISWA DUA BILANGAN CACAH BERSELISIH 7

PERTANYAAN DARI SISWA DUA BILANGAN CACAH BERSELISIH 7, BILA HASIL KALI 2 BILANGAN ITU ADALAH 120, TENTUKANLAH BILANGAN– BILANGAN ITU

Pembahasan : a=b– 7 a x b = 120 ( b – 7 ) x b = 120 b 2 – 7 b -120 = 0 (b – 15) (b + 8)

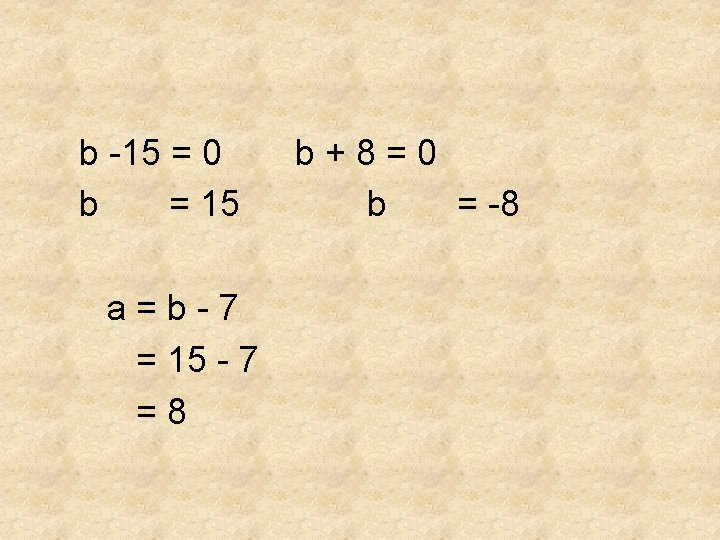
b -15 = 0 b = 15 a=b-7 = 15 - 7 =8 b+8=0 b = -8

Soal - 1 • Fungsi g dirumuskan dengan : g(x) = x 2 – 1 • Jika peta dari m adalah 24 • Tentukan nilai dari m

Pembahasan • Peta dari m : (m) = m 2 – 1 = 24 m 2 = 24 + 1 m 2 = 25 m = 5

Soal - 2 • Diketahui : f( x + 3 ) = 2 x + 5 • Tentukan nilai dari : a. f (10) b. f (15)

Pembahasan • f(10) = f( 7 + 3 ) • f(15) = f( 12 + 3 ) f(x + 3 ) = 2 x + 5 f (x )= 2(12 ) + 5 f(x)= 2(7 ) + 5 = 24 + 5 = 14 + 5 = 29 = 19 • F(15) = 29 F(10) = 19

Soal - 3 • Diketahui ; f(x) = 3 x + n dan f(-1) = 7 Tentukan nilai dari : a. f(5) – f(1) =. . . b. f(6) + f(2) =. . .

Pembahasan • F(x) = 3 x + n F(-1) = 3(-1) + n = 7 • Jadi f(x) = 3 x + 10 f(1) = 3(1) + 10 = 13 f(2) = 3(2) + 10 = 16 f(5) = 3(5) + 10 = 25 f(6) = 3(6) + 10 = 28 • F(5) – f(1) = 25 – 13 = 12 • F(6) + f(2) = 28 + 16 = 42

Soal - 4 • Diketahui ; f(x) = ax + b f(1) = - 2 f(4) = 19 Tentukan nilai dari a

Pembahasan • F(x)= ax + b f(1) = a + b = -2 f(4) = 4 a + b = 19 a + b = -2 3 a = 21 a= 7 Jadi, nilai dari a = 7

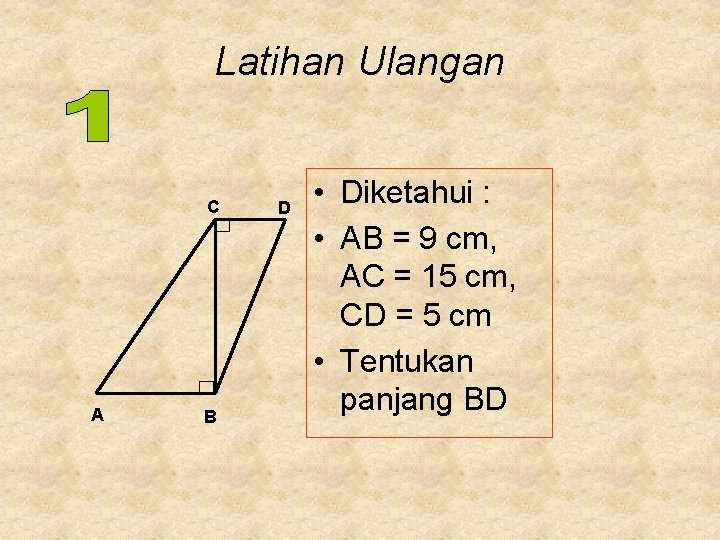
Latihan Ulangan C A B D • Diketahui : • AB = 9 cm, AC = 15 cm, CD = 5 cm • Tentukan panjang BD

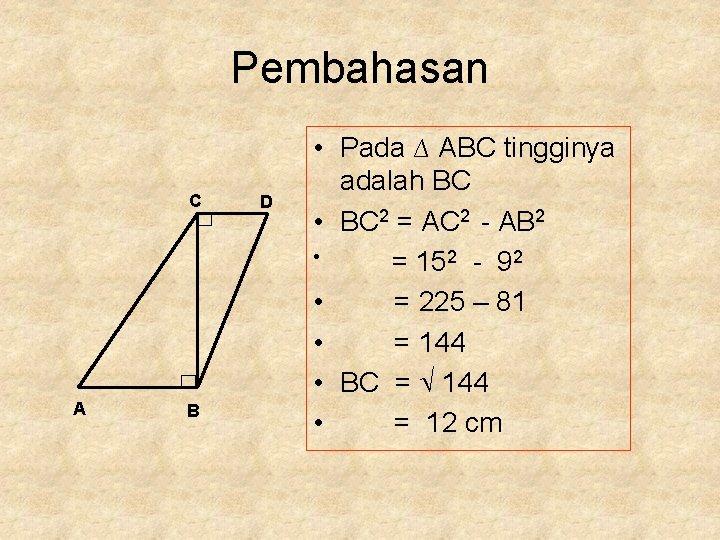
Pembahasan C A B D • Pada ∆ ABC tingginya adalah BC • BC 2 = AC 2 - AB 2 • = 152 - 92 • = 225 – 81 • = 144 • BC = 144 • = 12 cm

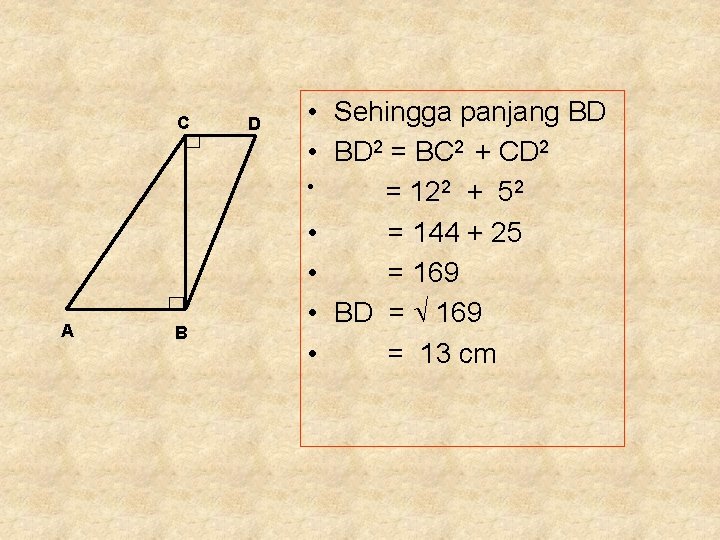
C A B D • Sehingga panjang BD • BD 2 = BC 2 + CD 2 • = 122 + 52 • = 144 + 25 • = 169 • BD = 169 • = 13 cm

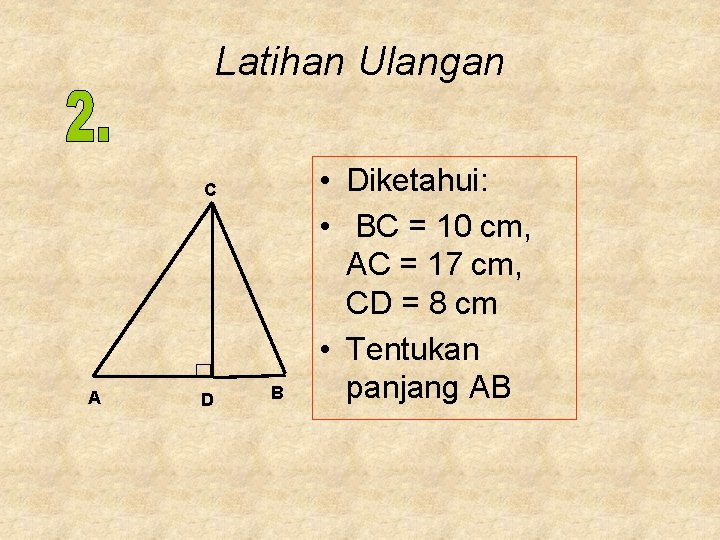
Latihan Ulangan C A D B • Diketahui: • BC = 10 cm, AC = 17 cm, CD = 8 cm • Tentukan panjang AB

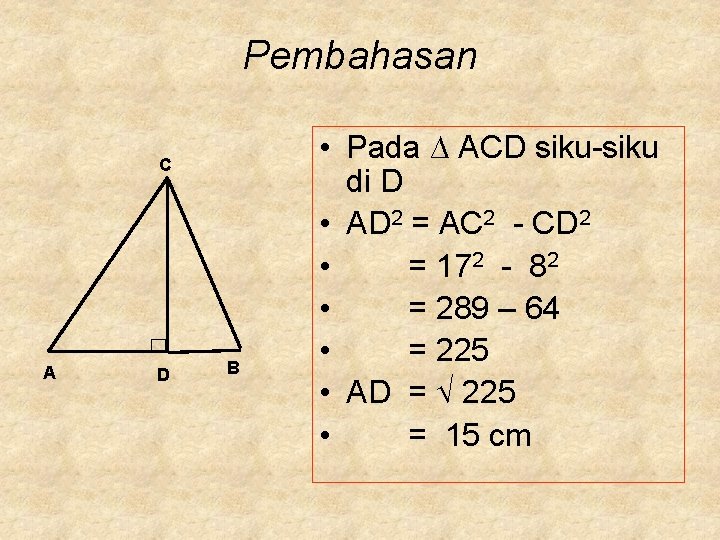
Pembahasan C A D B • Pada ∆ ACD siku-siku di D • AD 2 = AC 2 - CD 2 • = 172 - 82 • = 289 – 64 • = 225 • AD = 225 • = 15 cm

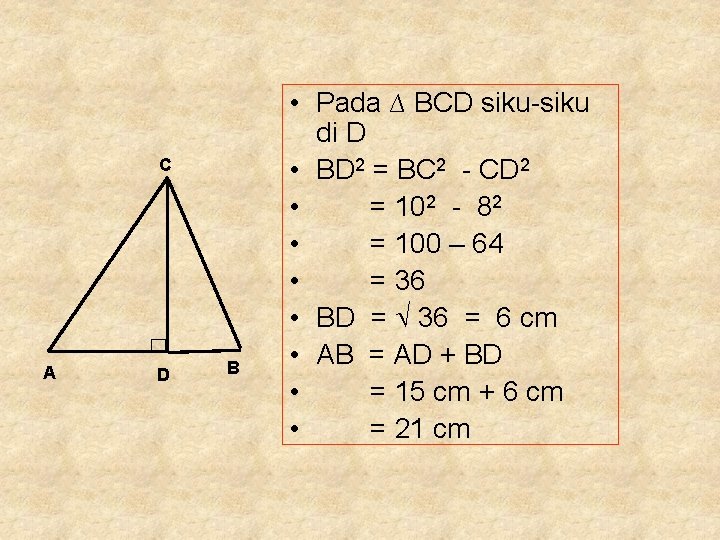
C A D B • Pada ∆ BCD siku-siku di D • BD 2 = BC 2 - CD 2 • = 102 - 82 • = 100 – 64 • = 36 • BD = 36 = 6 cm • AB = AD + BD • = 15 cm + 6 cm • = 21 cm

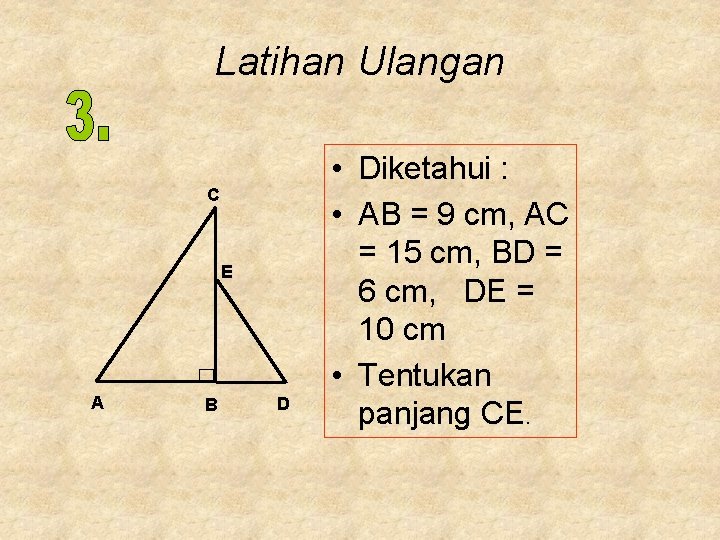
Latihan Ulangan C E A B D • Diketahui : • AB = 9 cm, AC = 15 cm, BD = 6 cm, DE = 10 cm • Tentukan panjang CE.

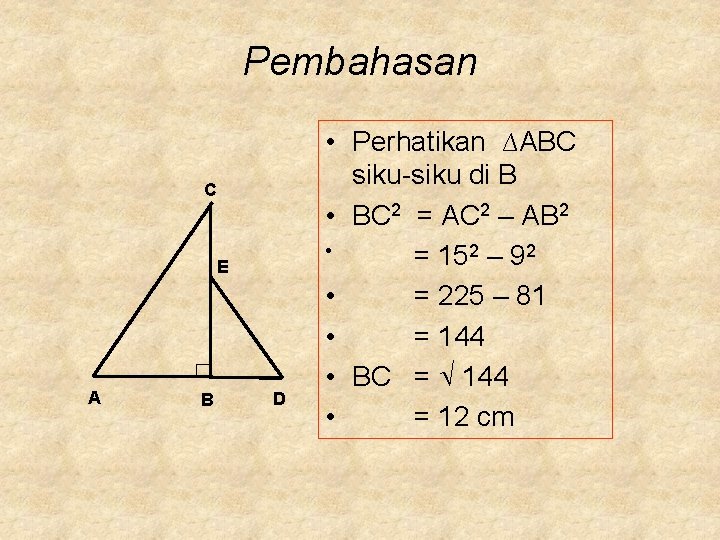
Pembahasan C E A B D • Perhatikan ∆ABC siku-siku di B • BC 2 = AC 2 – AB 2 • = 152 – 92 • = 225 – 81 • = 144 • BC = 144 • = 12 cm

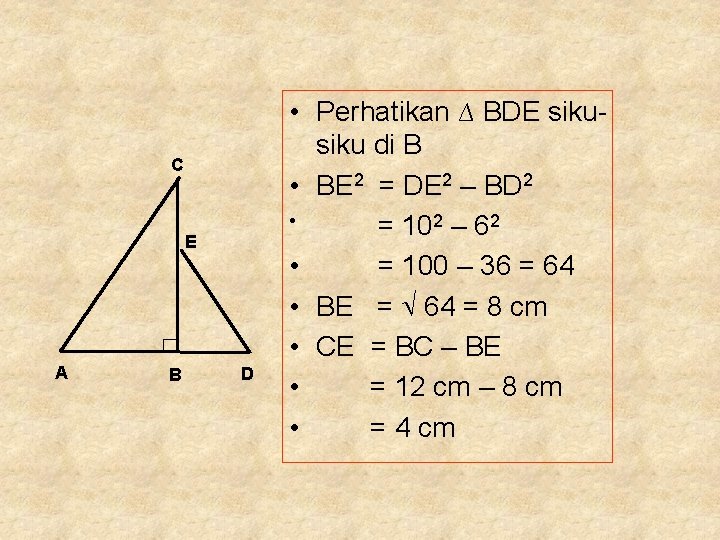
C E A B D • Perhatikan ∆ BDE siku di B • BE 2 = DE 2 – BD 2 • = 102 – 62 • = 100 – 36 = 64 • BE = 64 = 8 cm • CE = BC – BE • = 12 cm – 8 cm • = 4 cm

SOAL - 1 • Harga 35 buku Rp 122. 500, - Untuk membeli 24 buku tersebut diperlukan uang sebanyak. . . a. Rp 80. 000, b. Rp 84. 000, c. Rp 86. 000, d. Rp 96. 00, -

Pembahasan • 35 buku = Rp 122. 500 • 24 buku = Rp x Gunakan cara perbandingan : X = ( 24 : 35 ) x Rp 122. 500, = Rp 84. 000, -

SOAL - 2 • Harga 3 lusin pensil Rp 45. 000, -. Harga 32 pensil tersebut adalah … a. Rp 32. 000, b. Rp 34. 000, c. Rp 36. 000, d. Rp 40. 000, -

Pembahasan • 3 lusin = Rp 45. 000, • 32 buah = Rp x • 3 lusin = 36 buah x = ( 32 : 36 ) x Rp 45. 000, = Rp 40. 000, -

SOAL - 3 • Harga 5 buku tulis = Rp 3. 500, -. Seorang anak mempunyai uang Rp 15. 000, - yang akan dibelikan buku tulis yang sama sebanyaknya. Banyak uang kembalian yang diterima anak tersebut adalah. . . a. b. c. d. Rp Rp 200, 00 300, 00 400, 00 500, 00

Pembahasan • 5 buku = Rp 3, 500, • Rp 15. 000 = x Buku • 1 buku = Rp 3. 500 : 5 = Rp 700, • Maksimal x = ( 15. 000 : 700 ) = 21 buku = 21 x Rp 700 = Rp 14. 700, Sisa uang = Rp 15. 000 – Rp 14. 700 = Rp 300, -

Soal - 4 • Dengan 9 liter bensin sebuah mobil dapat menempuh jarak 72 km. Banyak liter bensin yang diperlukan untuk menempuh jarak 108 km adalah. . . a. 15 liter b. 13, 5 liter c. 8 liter d. 6 liter

Pembahasan • 9 liter = 72 km • X liter = 108 km X = ( 108 : 72 ) x 9 liter =13, 5 liter

Soal - 5 • Jarak kota A ke B adalah 85 km. Suatu peta mempunyai skala 1 : 500. 000, maka jarak kedua kota pada peta adalah. . a. 0, 17 cm b. 1, 7 cm c. 17 cm d. 170 cm

Pembahasan • Jarak sebenarnya = 85 km = 8. 500. 000 cm • Skala 1 : 500. 000 Jarak pada peta : ( 8. 500. 000 : 500. 000 ) = 17 cm

Soal - 6 • Jarak 490 km ditempuh sebuah mobil dengan bensin 35 liter. Jika mobil tersebut menghabiskan bensin 40 liter, maka jarak yang ditempuhnya adalah. . . a. 420 km b. 450 km c. 550 km d. 560 km

Pembahasan • 490 km • x km = = 35 liter 40 liter X = ( 40 : 35 ) x 490 km = 640 km

Soal - 7 • Untuk membuat 12 kue diperlukan gula halus sebanyak 600 gram, untuk membuat 60 kue diperlukan gula halus sebanyak. . . a. 1200 gram b. 1800 gram c. 2400 gram d. 3000 gram

Pembahasan • 12 kue = 600 gram • 60 kue = x gram X = ( 60 : 12 ) x 600 gram = 3. 000 gram

Soal - 1 • Dalam seleksi penerima beasiswa, setiap siswa harus lulus tes matematika dan bahasa. Dari 180 peserta terdapat 103 orang dinyatakan lulus tes matematika dan 142 orang lulus tes bahasa. Banyak siswa yang dinyatakan lulus sebagai penerima beasiswa ada. . a. 38 orang c. 65 orang c. 45 orang d. 77 orang

Pembahasan • • n(S) = 180 orang n(M) = 103 orang n(B) = 142 orang n(M B ) = x orang n(S) = n( M B ) = n(M) + n(B) – n( M B) 180 = 103 + 142 - X X = 245 – 180 = 65 Jadi yang lulus adalah 65 orang = ( C )

LATIHAN - 2 • Sebuah RS mempunyai pasien sebanyak 53 orang, 26 orang menderita demam ber- arah, dan 32 orang menderita muntaber. penderita DBD dan muntaber 7 orang, yang tidak menderita DBD atau muntaber adalah … a. 2 orang c. 5 orang b. 3 orang d. 6 orang

Pembahasan • • • Jumlah pasien = 53 orang. Demam berdarah = 26 orang. Muntaber = 32 orang. DBD dan muntaber = 7 orang. Bkn DBD atau muntaber = X orang. X = ( 53 org ) - ( 26 org + 32 org – 7 ) X = 53 org – 51 org X = 2 orang

LATIHAN - 3 • Dari 40 orang anak, ternyata 24 anak gemar minum teh, 18 anak gemar minum kopi, 5 anak tidak gemar minum keduanya Banyaknya anak yang gemar keduanya adalah. . . a. 2 orang b. 5 orang c. 7 orang d. 9 orang

Pembahasan • • • Jumlah anak = 40 orang The = 24 orang Kopi = 18 orang Teh dan Kopi = x orang Tidak keduanya = 5 orang (24 + 18 ) - x = 40 - 5 42 - x = 35 x = 42 - 35 = 7 Yang gemar keduanya adalah 7 anak.

LATIHAN - 4 • Dari 60 orang siswa ternyata 36 orang gemar membaca, 34 orang gemar menulis, 12 orang gemar kedua-duanya. Banyaknya anak yang tidak mengemari keduanya adalah. . . a. 2 orang b. 5 orang c. 7 orang d. 9 orang

Pembahasan • • • Jumlah anak = 60 orang Membaca = 36 orang Menulis = 34 orang Membaca dan menulis = 12 orang Tidak keduanya = x orang (36 + 34 ) - 12 = 60 - x 58 = 60 - x x = 60 – 58 x = 2

LATIHAN - 5 • Jika himpunan B A dengan n(A) = 25 dan n(B) = 17, maka n ( A B ) =. . . a. b. c. d. 8 11 17 25

Pembahasan • • • n ( A ) = 25 n ( B ) = 17 Setiap B A, maka A B = A Sehingga n ( A B ) = n ( A ) n ( A B ) = 25

LATIHAN - 6 • Dalam sebuah kelas terdapat 20 siswa gemar matematika, 15 siswa gemar fisika, 8 siswa gemar keduanya. Banyak siswa dalam kelas adalah. . . a. 23 siswa b. 27 siswa c. 28 siswa d. 43 siswa

Pembahasan • • n(M) = 20 orang n(F) = 15 orang n(M F ) = 8 orang n( M F ) = n(M) + n(F) – n(M F ) = 20 + 15 – 8 = 35 – 8 = 27 orang

SELAMAT BELAJAR