Bab 1 Analisa Vektor Notasi Vektor Vektor A

Bab 1 Analisa Vektor

Notasi Vektor Ø Vektor A dapat dituliskan dalam bentuk komponen-komponen vektor satuan sebagai A = Axax + Ayay + Azaz Ø Dalam bentuk komponen-komponennya, magnituda vektor A didefinisikan sebagai |A| =A= Ø Vektor satuan sepanjang arah A diberikan oleh

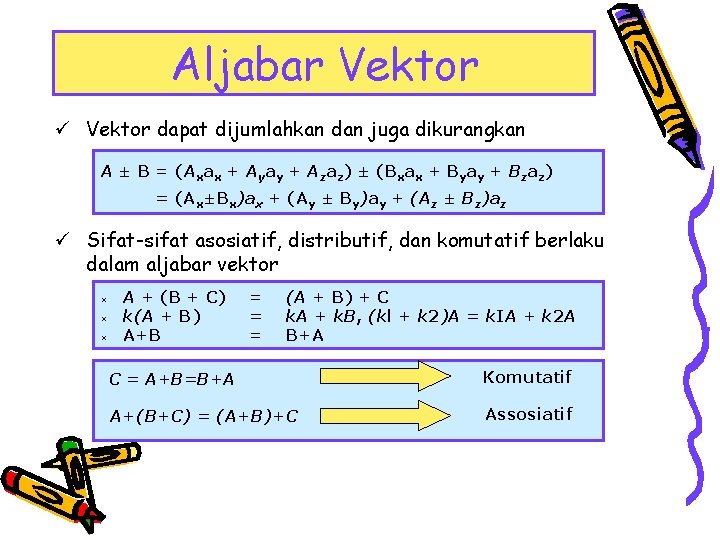
Aljabar Vektor ü Vektor dapat dijumlahkan dan juga dikurangkan A ± B = (Axax + Ayay + Azaz) ± (Bxax + Byay + Bzaz) = (Ax±Bx)ax + (Ay ± By)ay + (Az ± Bz)az ü Sifat-sifat asosiatif, distributif, dan komutatif berlaku dalam aljabar vektor × × × A + (B + C) k(A + B) A+B = = = (A + B) + C k. A + k. B, (kl + k 2)A = k. IA + k 2 A B+A C = A+B=B+A Komutatif A+(B+C) = (A+B)+C Assosiatif

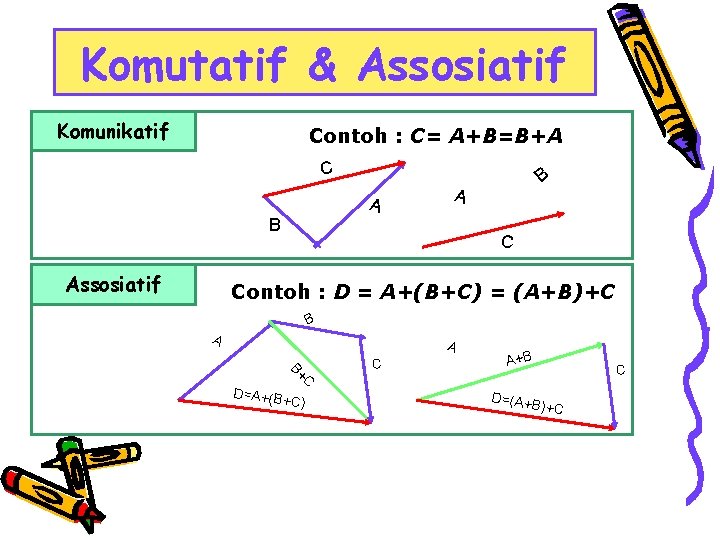
Komutatif & Assosiatif Komunikatif Contoh : C= A+B=B+A C A A B Assosiatif B C Contoh : D = A+(B+C) = (A+B)+C B A A C B+ D=A+(B+ C) C A+B D=(A+ B)+C C

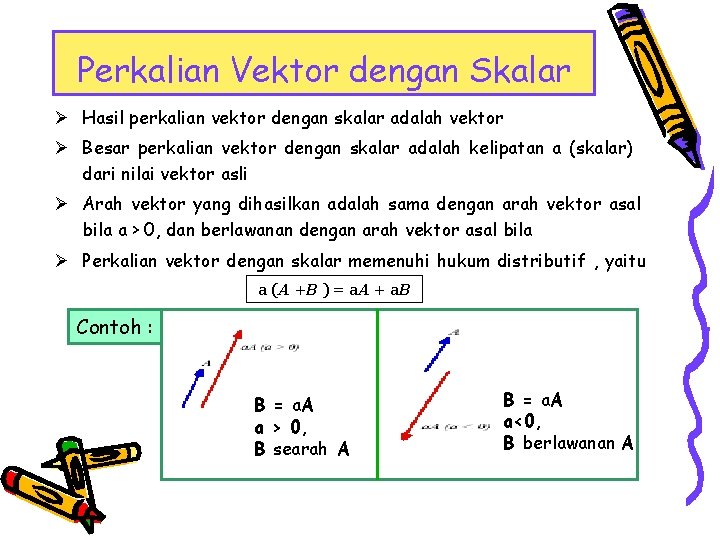
Perkalian Vektor dengan Skalar Ø Hasil perkalian vektor dengan skalar adalah vektor Ø Besar perkalian vektor dengan skalar adalah kelipatan a (skalar) dari nilai vektor asli Ø Arah vektor yang dihasilkan adalah sama dengan arah vektor asal bila a > 0, dan berlawanan dengan arah vektor asal bila Ø Perkalian vektor dengan skalar memenuhi hukum distributif , yaitu a (A +B ) = a. A + a. B Contoh : B = a. A a > 0, B searah A B = a. A a<0, B berlawanan A

Perkalian Titik (Dot) Dua Vektor Ø A • B = AB cos (dibaca sebagai "A titik B") Ø Hasil perkalian titik atau dot product adalah besaran skalar Ø Perkalian titik adalah komutatif Ø Perkalian titik adalah distributif A. B = B. A A. (B+C) = A. B + A. C Ø Perkalian titik memenuhi perkalian skalar A • k. B = k(A • B) Contoh : di mana adalah sudut antara A dan B yang lebih kecil. Dalam bentuk komponen, perkalian titik adalah sama dengan A • B = Ax. Bx + Ay. By + Az. Bz

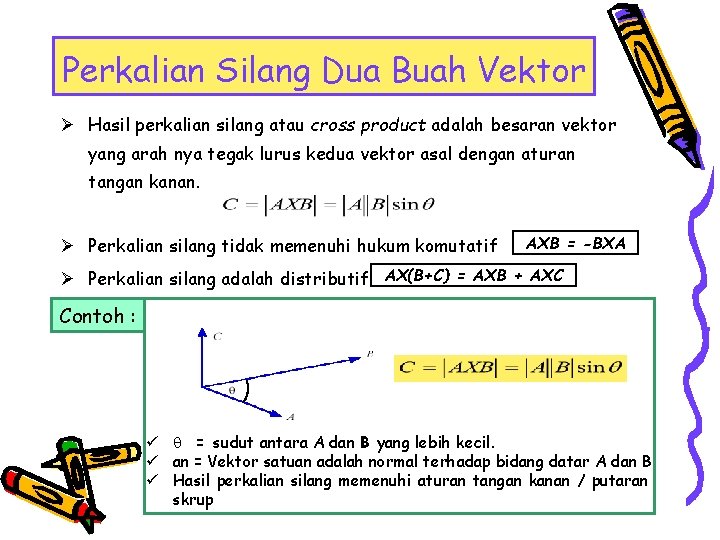
Perkalian Silang Dua Buah Vektor Ø Hasil perkalian silang atau cross product adalah besaran vektor yang arah nya tegak lurus kedua vektor asal dengan aturan tangan kanan. Ø Perkalian silang tidak memenuhi hukum komutatif AXB = -BXA Ø Perkalian silang adalah distributif AX(B+C) = AXB + AXC Contoh : ü = sudut antara A dan B yang lebih kecil. ü an = Vektor satuan adalah normal terhadap bidang datar A dan B ü Hasil perkalian silang memenuhi aturan tangan kanan / putaran skrup

ü Perluasan perkalian silang dalam bentuk komponen-komponen vektor akan menghasilkan, A x B = (Axax + Ayay + Azaz) x (Bxax + Byay + Bzaz) = (AYBZ – Az. Bz)ax + (Az. Bx - Ax. Bz)ay + (Ax. By – Ay. Bx)az Contoh : Jika A = 2 ax + 4 ay – 3 a. Z dan B = ax – ay, carilah A • B dan A x B ! Penyelesaian!

Sistem koordinat • Koordinat cartesian tidak cukup !!! • Terdapat beberapa kasus yang akan lebih mudah penyelesaiannya dengan menggunakan koordinat tabung dan bola • Sebagai contoh, persoalan kabel yang menggunakan koordinat silindris dan persoalan antena yang memiliki penyelesaian menggunakan koordinat bola. • Ilustrasi : • Titik P digambarkan dalam 3 buah koordinat • Koordinat cartesian = (x, y, z) • koordinat silindris = (r, , z ) • koordinat bola = (r, , )

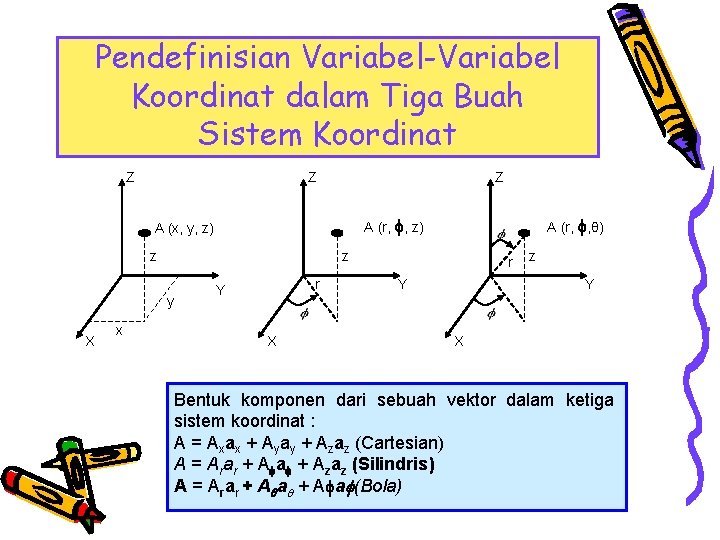
Pendefinisian Variabel-Variabel Koordinat dalam Tiga Buah Sistem Koordinat Z Z Z AA(r, φ, , z)z) A (x, y, z) z z y X x A (r, , θ) r Y X r Y z Y X Bentuk komponen dari sebuah vektor dalam ketiga sistem koordinat : A = Axax + Ayay + Azaz (Cartesian) A = Arar + A a + Azaz (Silindris) A = Arar + A a (Bola)

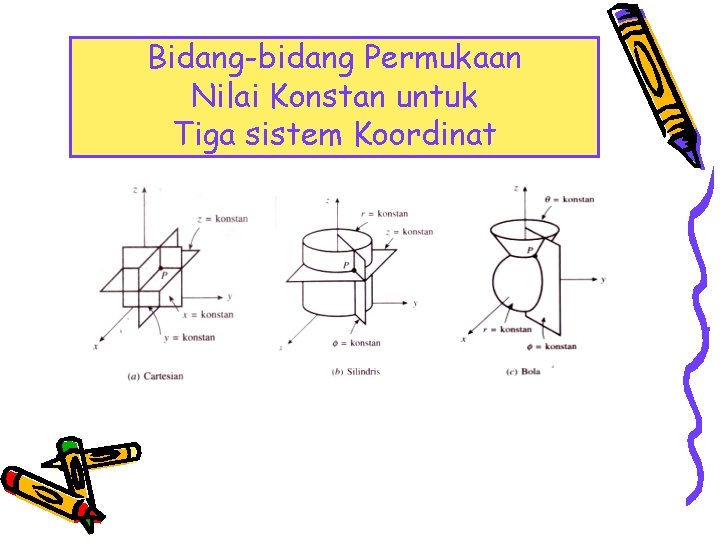
Bidang-bidang Permukaan Nilai Konstan untuk. Tiga sistem Koordinat

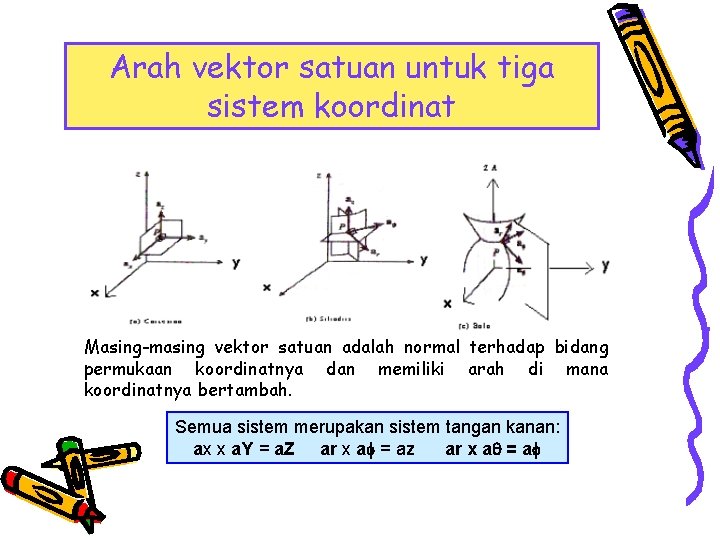
Arah vektor satuan untuk tiga sistem koordinat Masing-masing vektor satuan adalah normal terhadap bidang permukaan koordinatnya dan memiliki arah di mana koordinatnya bertambah. Semua sistem merupakan sistem tangan kanan: ax x a. Y = a. Z ar x a = az ar x a = a

Transformasi skalar antar sistem koordinat Koordinat cartesian – koordinat silinder vektor dalam Cartesian : A = Axax + Ayay + Azaz Dengan masing-masing komponen merupakan fungsi dari x, y dan z; vektor dalam Silinder : Dengan masing-masing komponen merupakan fungsi dari r, θ dan z;

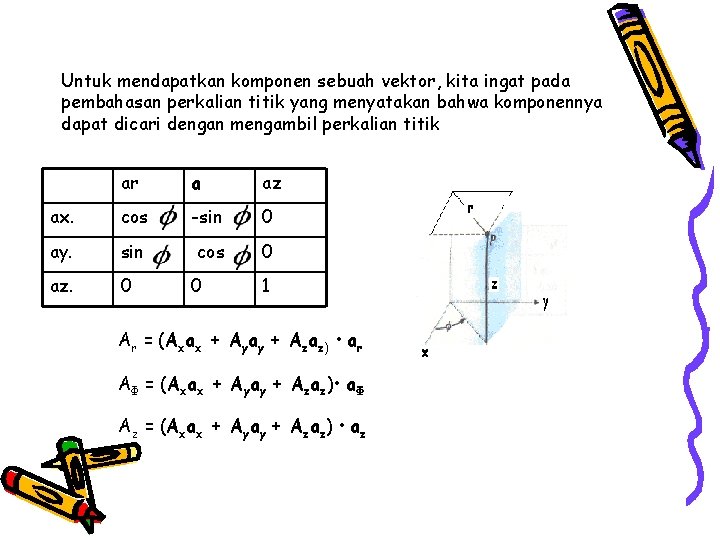
Untuk mendapatkan komponen sebuah vektor, kita ingat pada pembahasan perkalian titik yang menyatakan bahwa komponennya dapat dicari dengan mengambil perkalian titik ar a az ax. cos -sin 0 ay. sin cos 0 az. 0 0 1 Ar = (Axax + Ayay + Azaz) • ar AΦ = (Axax + Ayay + Azaz) • aΦ Az = (Axax + Ayay + Azaz) • az

Transformasi skalar antar sistem koordinat Koordinat cartesian – koordinat bola vektor dalam Cartesian : A = Axax + Ayay + Azaz Dengan masing-masing komponen merupakan fungsi dari x, y dan z; vektor dalam Silinder : Dengan masing-masing komponen merupakan fungsi dari r, θ dan z;

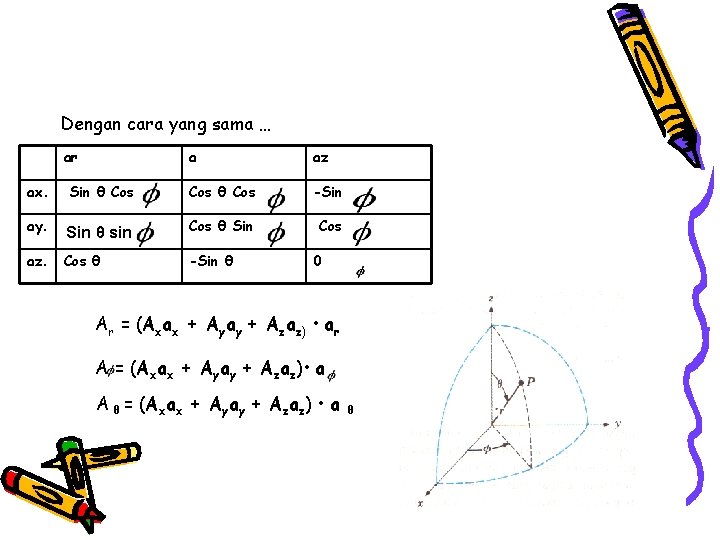
Dengan cara yang sama … ar a az ax. Sin θ Cos -Sin ay. Sin θ sin Cos θ Sin Cos az. Cos θ -Sin θ 0 Ar = (Axax + Ayay + Azaz) • ar A = (Axax + Ayay + Azaz) • a A θ = (Axax + Ayay + Azaz) • a θ

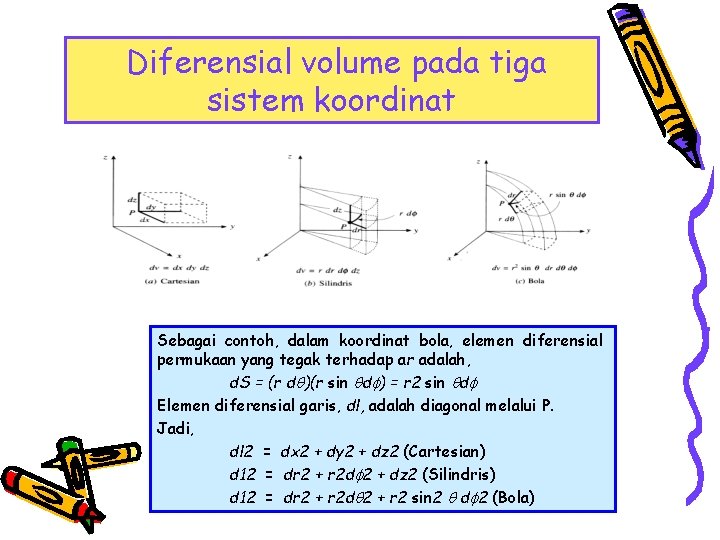
Diferensial volume pada tiga sistem koordinat Sebagai contoh, dalam koordinat bola, elemen diferensial permukaan yang tegak terhadap ar adalah, d. S = (r d )(r sin d ) = r 2 sin d Elemen diferensial garis, dl, adalah diagonal melalui P. Jadi, dl 2 = dx 2 + dy 2 + dz 2 (Cartesian) d 12 = dr 2 + r 2 d 2 + dz 2 (Silindris) d 12 = dr 2 + r 2 d 2 + r 2 sin 2 d 2 (Bola)

Soal-soal dan Penyelesaiannya Soal 1 Carilah vektor C yang memiliki arah dari M(x 1, y 1, z 1) ke N(x 2, y 2, z 2)! Berapakah magnituda dari vektor ini dan vektor satuan arahnya? Penyelesaian : Koordinat-koordinat titik M dan N digunakan untuk menuliskan posisi dari kedua vektor A dan B pada Gambar 1 -6. Selanjutnya. C = B – A = (x 2 – x 1)ax + (y 2 – y 1)ay + (z 2 – z 1)az Magnituda C adalah Vektor satuannya adalah

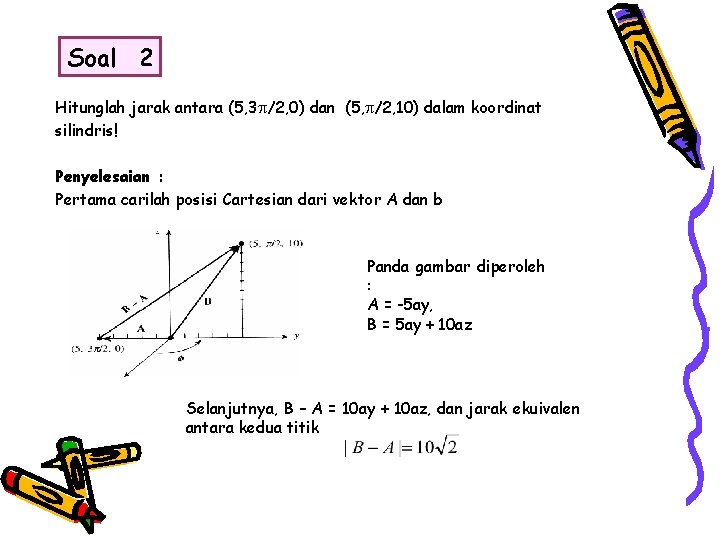
Soal 2 Hitunglah jarak antara (5, 3 /2, 0) dan (5, /2, 10) dalam koordinat silindris! Penyelesaian : Pertama carilah posisi Cartesian dari vektor A dan b Panda gambar diperoleh : A = -5 ay, B = 5 ay + 10 az Selanjutnya, B – A = 10 ay + 10 az, dan jarak ekuivalen antara kedua titik

Soal 3 Diberikan A = (y – 1 )ax+2 xay, carilah vektor pada (2, 2, 1) dan proyeksinya pada vektor B = 5 ax – ay + 2 az! Penyelesaian : A = (2 – 1)ax + 2(2)ay = ax + 4 ay. Seperti ditunjukkan pada Gambar, proyeksi sebuah vektor pada vektor kedua dapat diperoleh dengan menyatakan vektor satuan yang searah dengan vektor kedua serta mengambil perkalian titiknya. Proyeksi A pada B = A a. B Proyeksi A pada B B Jadi pada (2, 2, 1) Proyeksi A pada B =

Soal 4 Gunakanlah sistem koordinat bola untuk memperoleh luas area dari sebuah lembaran tipis pada selubung bola dengan jari r = r ( Gambar 1 -9). Berapakah luas area yang diperoleh jika = 0 dan = ? Penyelesaian : Diferensial elemen permukaan adalah [ lihat Gambar diferensial volume pada tiga sistem koordinat Bola ] d. S = r 02 sin d d Selanjutnya, sehingga saat = 0 dan = , A = 4 r 02, yang merupakan luas permukaan bola.