SISTEM KOORDINAT VEKTOR Tri Rahajoeningroem MT T Elektro

SISTEM KOORDINAT VEKTOR Tri Rahajoeningroem, MT T. Elektro - UNIKOM

Tujuan Pembelajaran • Mahasiswa dapat memahami koordinat vektor • Mahasiswa dapat menggunakan sistem koordinat vektor untuk menyelesaikan permasalahan dalam bidang medan elektromagnetik • Mahasiswa dapat mentransformasikan sistem koordinat satu dengan koordinat yang lain

Pokok bahasan Pokok Bahasan • Pengenalan sistem koordinat Kartesian, Silindris dan Bola • Penggunaan sistem koordinat Kartesian, Silindris dan Bola serta contoh-contoh soal-soal. • Meninjau aplikasi dari analisa vektor ini dimana terdapat dalam bidang listrik dan gelombang, mekanika teknik, mekanika zat alir dan lain-lain. 3

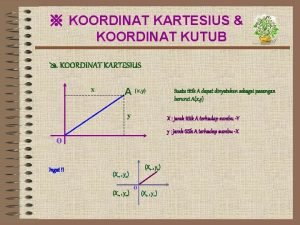
Kegunaan Sistem koordinat • Untuk dapat menjabarkan sebuah vektor secara akurat, kita harus memberikan vektor yang bersangkutan suatu panjang, arah, sudut dan proyeksi-proyeksi yang spesifik • Untuk itu diperlukan sistem koordinat dalam analisis vektor • Ada 3 sistem koordinat yang akan kita gunakan : 1. Koordinat cartesian (persegi) 2. Koordinat Silindris 3. Koordinat Bola

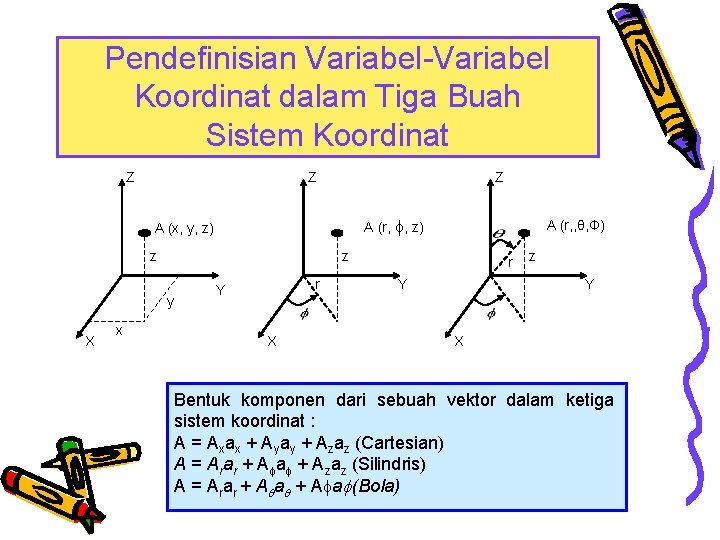
Sistem koordinat • Koordinat cartesian tidak cukup !!! • Terdapat beberapa kasus yang akan lebih mudah penyelesaiannya dengan menggunakan koordinat tabung dan bola • Sebagai contoh, persoalan kabel yang menggunakan koordinat silindris dan persoalan antena yang memiliki penyelesaian menggunakan koordinat bola. • Ilustrasi : • Titik A digambarkan dalam 3 buah koordinat • Koordinat cartesian = (x, y, z) • koordinat silindris = (r, , z ) • koordinat bola = (r, , )

Pendefinisian Variabel-Variabel Koordinat dalam Tiga Buah Sistem Koordinat Z Z Z AA(r, φ, , z)z) A (x, y, z) z z y X x A (r, , θ, Φ) r Y X r Y z Y X Bentuk komponen dari sebuah vektor dalam ketiga sistem koordinat : A = Axax + Ayay + Azaz (Cartesian) A = Arar + A a + Azaz (Silindris) A = Arar + A a (Bola)

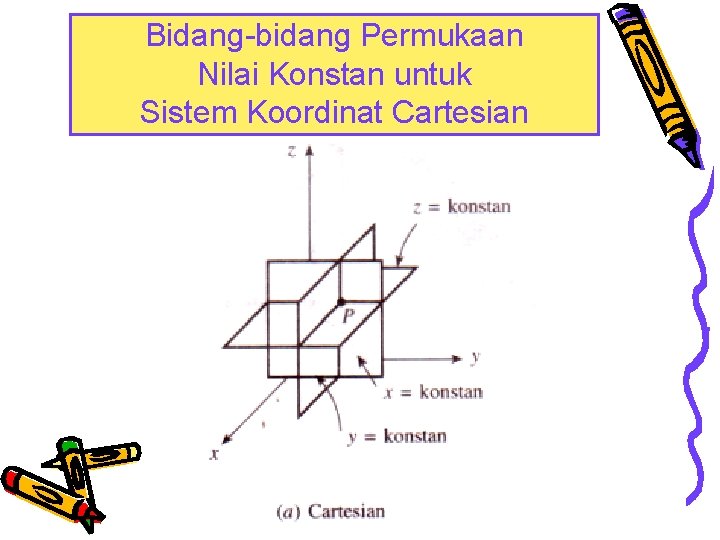
Bidang-bidang Permukaan Nilai Konstan untuk Sistem Koordinat Cartesian.

Bidang-bidang Permukaan Nilai Konstan untuk. Sistem Koordinat Silindris

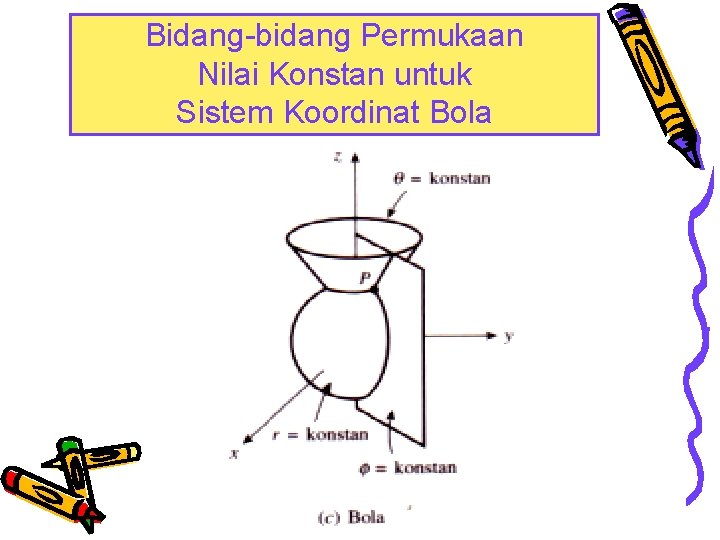
Bidang-bidang Permukaan Nilai Konstan untuk Sistem Koordinat Bola.

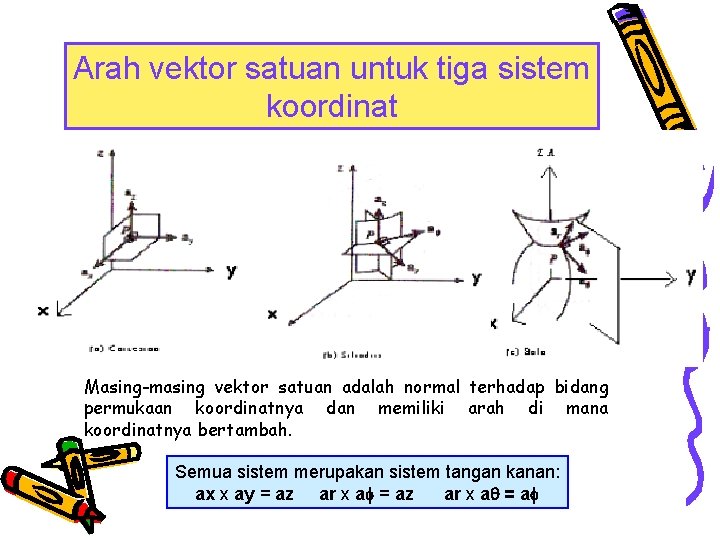
Arah vektor satuan untuk tiga sistem koordinat Masing-masing vektor satuan adalah normal terhadap bidang permukaan koordinatnya dan memiliki arah di mana koordinatnya bertambah. Semua sistem merupakan sistem tangan kanan: ax x ay = az ar x a = a

Transformasi skalar antar sistem koordinat Koordinat cartesian – koordinat silinder vektor dalam Cartesian : A = Axax + Ayay + Azaz Dengan masing-masing komponen merupakan fungsi dari x, y dan z; vektor dalam Silinder : Dengan masing-masing komponen merupakan fungsi dari r, Φ dan z;

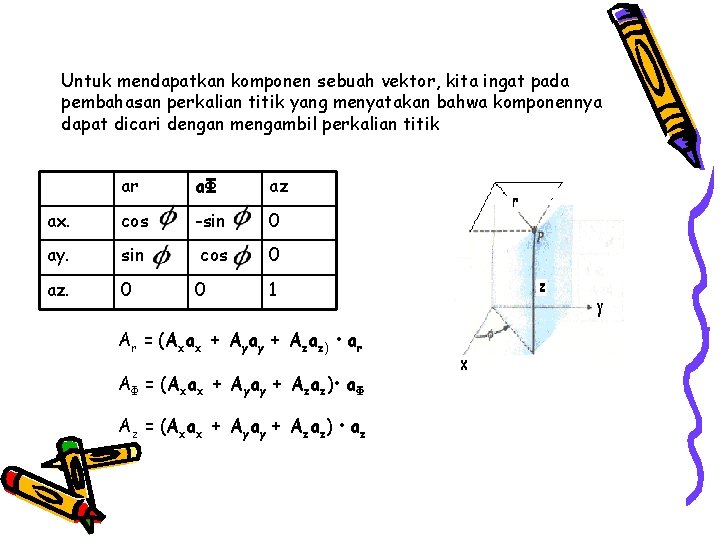
Untuk mendapatkan komponen sebuah vektor, kita ingat pada pembahasan perkalian titik yang menyatakan bahwa komponennya dapat dicari dengan mengambil perkalian titik ar aΦ az ax. cos -sin 0 ay. sin cos 0 az. 0 0 1 Ar = (Axax + Ayay + Azaz) • ar AΦ = (Axax + Ayay + Azaz) • aΦ Az = (Axax + Ayay + Azaz) • az

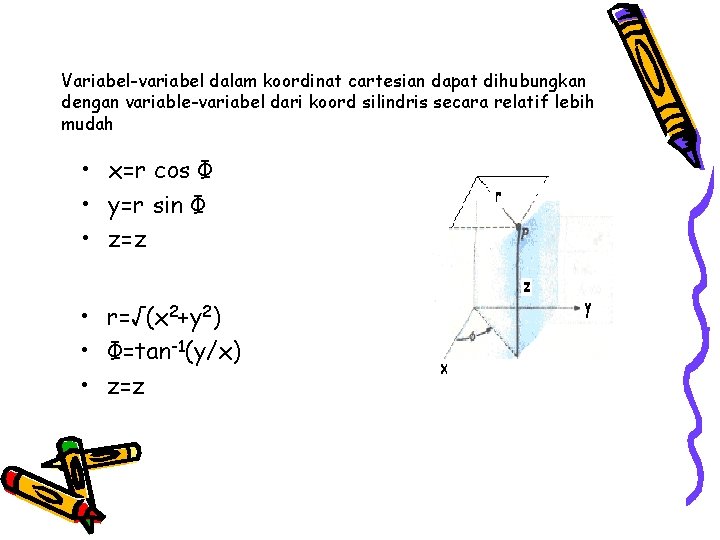
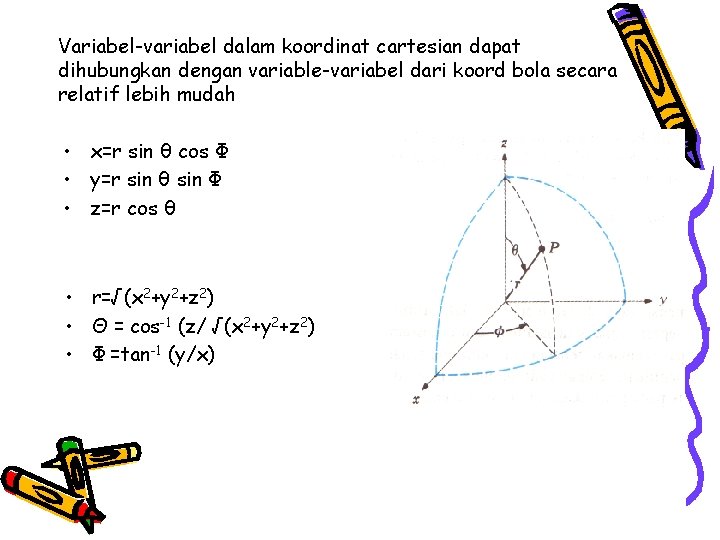
Variabel-variabel dalam koordinat cartesian dapat dihubungkan dengan variable-variabel dari koord silindris secara relatif lebih mudah • x=r cos Φ • y=r sin Φ • z=z • r=√(x 2+y 2) • Φ=tan-1(y/x) • z=z

Transformasi skalar antar sistem koordinat Koordinat cartesian – koordinat bola vektor dalam Cartesian : A = Axax + Ayay + Azaz Dengan masing-masing komponen merupakan fungsi dari x, y dan z; vektor dalam Bola : Dengan masing-masing komponen merupakan fungsi dari r, θ dan Φ

Dengan cara yang sama … ar ax. Sin θ Cos aθ aΦ Cos θ Cos -Sin Cos ay. Sin θ sin Cos θ Sin az. Cos θ -Sin θ 0 Ar = (Axax + Ayay + Azaz) • ar Aθ = (Axax + Ayay + Azaz) • aθ AΦ = (Axax + Ayay + Azaz) • aΦ

Variabel-variabel dalam koordinat cartesian dapat dihubungkan dengan variable-variabel dari koord bola secara relatif lebih mudah • x=r sin θ cos Φ • y=r sin θ sin Φ • z=r cos θ • r=√(x 2+y 2+z 2) • Θ = cos-1 (z/ √(x 2+y 2+z 2) • Φ =tan-1 (y/x)

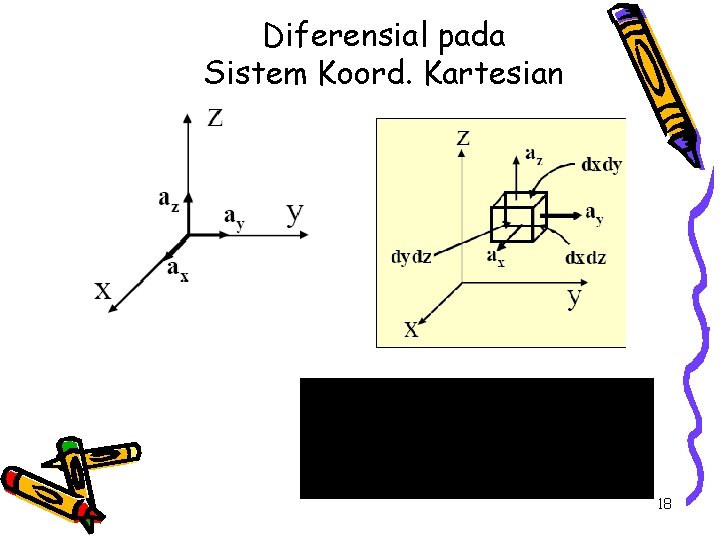
Diferensial pada Sistem Koord. Kartesian (x, y, z) Kuantitas diferensial: d. V, d. S and d ! x y z 17

Diferensial pada Sistem Koord. Kartesian 18

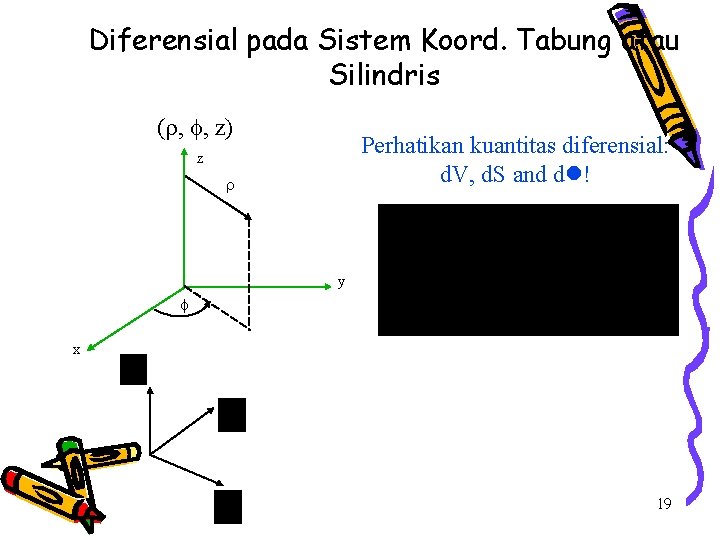
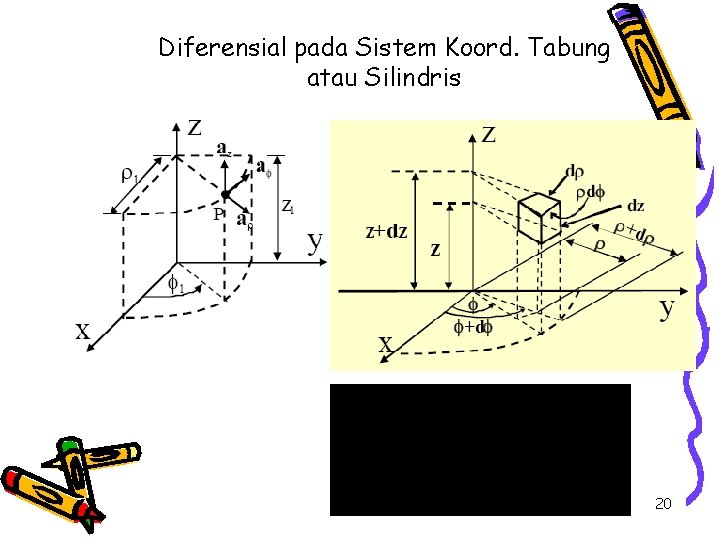
Diferensial pada Sistem Koord. Tabung atau Silindris ( , , z) Perhatikan kuantitas diferensial: d. V, d. S and d ! z y x 19

Diferensial pada Sistem Koord. Tabung atau Silindris 20

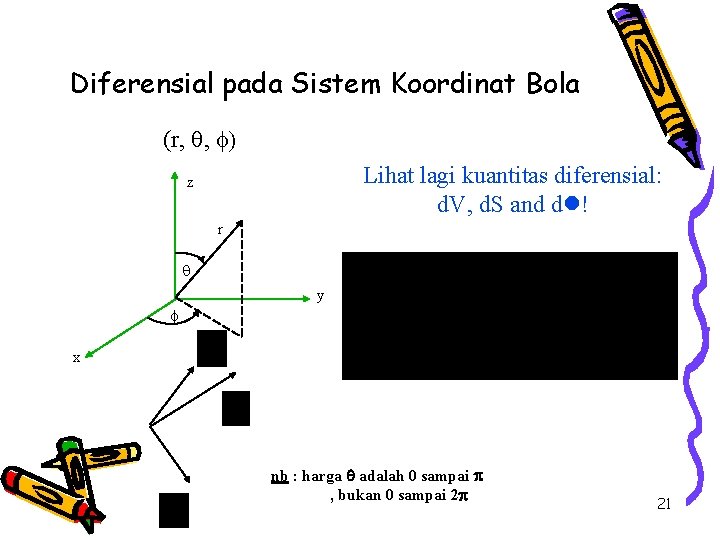
Diferensial pada Sistem Koordinat Bola (r, , ) Lihat lagi kuantitas diferensial: d. V, d. S and d ! z r y x nb : harga adalah 0 sampai , bukan 0 sampai 2 21

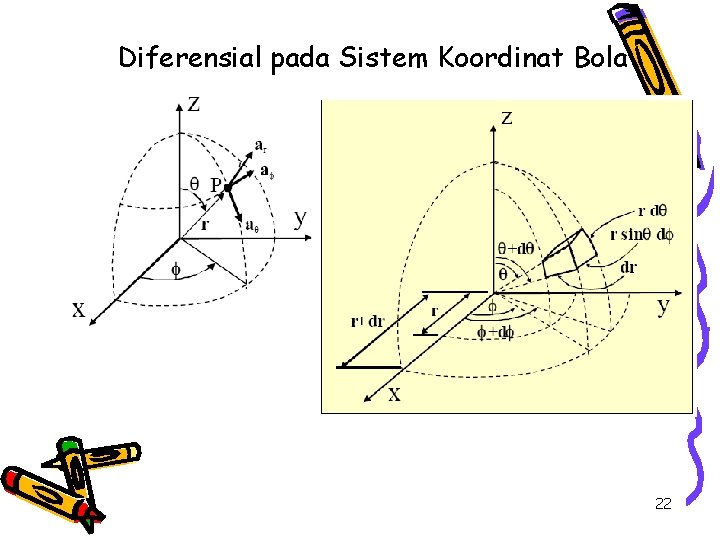
Diferensial pada Sistem Koordinat Bola 22

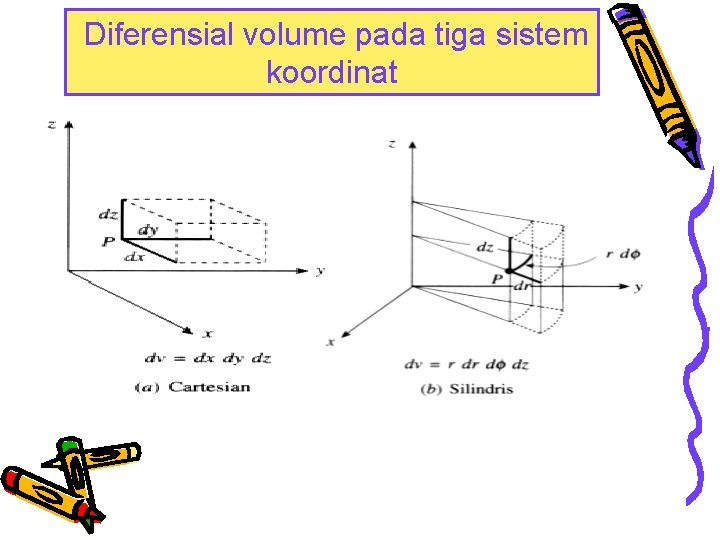
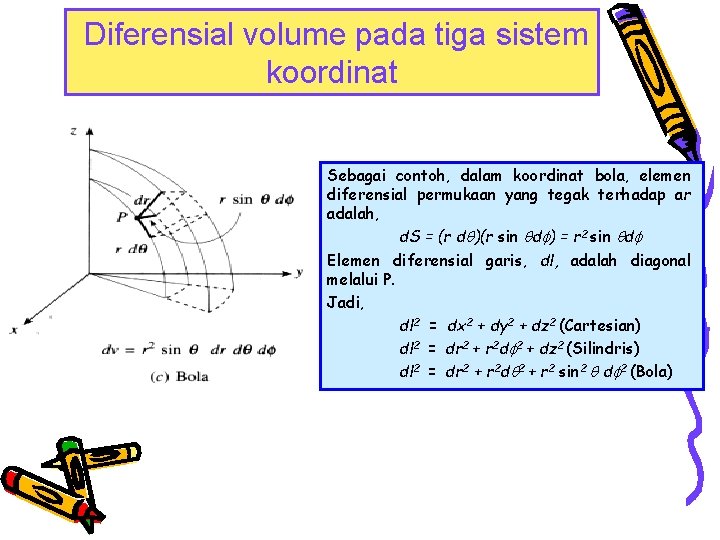
Diferensial volume pada tiga sistem koordinat

Diferensial volume pada tiga sistem koordinat Sebagai contoh, dalam koordinat bola, elemen diferensial permukaan yang tegak terhadap ar adalah, d. S = (r d )(r sin d ) = r 2 sin d Elemen diferensial garis, dl, adalah diagonal melalui P. Jadi, dl 2 = dx 2 + dy 2 + dz 2 (Cartesian) dl 2 = dr 2 + r 2 d 2 + dz 2 (Silindris) dl 2 = dr 2 + r 2 d 2 + r 2 sin 2 d 2 (Bola)

Soal-soal dan Penyelesaiannya Soal 1 Carilah vektor C yang memiliki arah dari M(x 1, y 1, z 1) ke N(x 2, y 2, z 2)! Berapakah magnituda dari vektor ini dan vektor satuan arahnya? Penyelesaian : Koordinat-koordinat titik M dan N digunakan untuk menuliskan posisi dari kedua vektor A dan B pada Gambar 1 -6. Selanjutnya. C = B – A = (x 2 – x 1)ax + (y 2 – y 1)ay + (z 2 – z 1)az Magnituda C adalah Vektor satuannya adalah

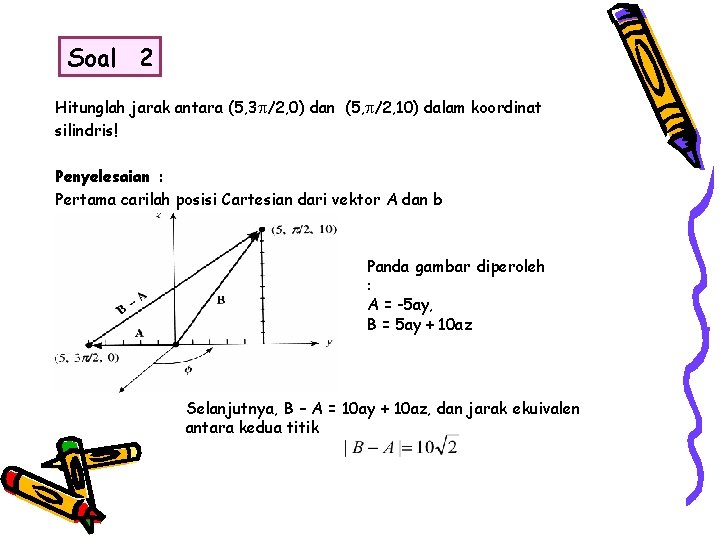
Soal 2 Hitunglah jarak antara (5, 3 /2, 0) dan (5, /2, 10) dalam koordinat silindris! Penyelesaian : Pertama carilah posisi Cartesian dari vektor A dan b Panda gambar diperoleh : A = -5 ay, B = 5 ay + 10 az Selanjutnya, B – A = 10 ay + 10 az, dan jarak ekuivalen antara kedua titik

Soal 3 Diberikan A = (y – 1 )ax+2 xay, carilah vektor pada (2, 2, 1) dan proyeksinya pada vektor B = 5 ax – ay + 2 az! Penyelesaian : A = (2 – 1)ax + 2(2)ay = ax + 4 ay. Seperti ditunjukkan pada Gambar, proyeksi sebuah vektor pada vektor kedua dapat diperoleh dengan menyatakan vektor satuan yang searah dengan vektor kedua serta mengambil perkalian titiknya. Proyeksi A pada B = A a. B Proyeksi A pada B B Jadi pada (2, 2, 1) Proyeksi A pada B =