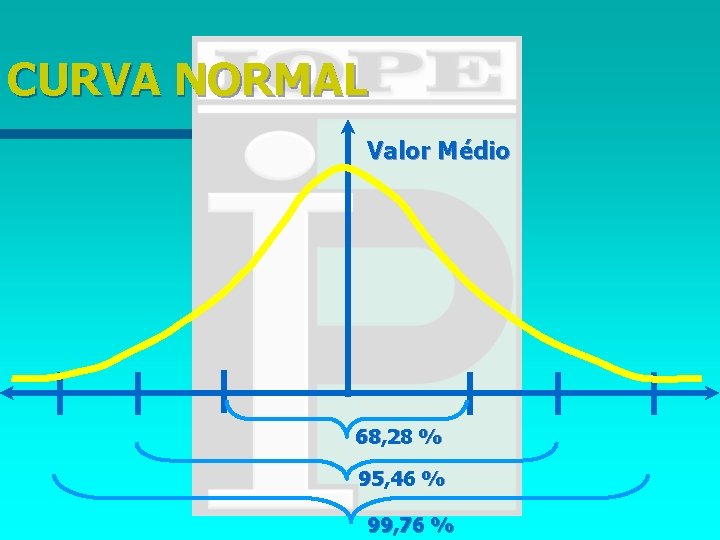
CURVA NORMAL Valor Mdio 68 28 95 46

CURVA NORMAL Valor Médio 68, 28 % 95, 46 % 99, 76 %

DISTRIBUIÇÃO NORMAL n Para conhecermos a probabilidade de encontrarmos valores em determinadas faixas da curva, devemos utilizar a tabela de constantes (tabela de distribuição normal) as quais podem ser usadas para declarar várias percentagens de intervalos de confiança.

DISTRIBUIÇÃO NORMAL n Para uma grandeza de entrada determinada por n observações repetidas independentes, podemos dizer que a incerteza padrão da média é o desvio padrão experimental da média.

DISTRIBUIÇÃO NORMAL n. A tabela da distribuição normal, permite utilizar a técnica mesmo para valores mais baixos de n, com poucas repetições.

CÁLCULO DE Z = = = valor desejado ; média ; desvio padrão.

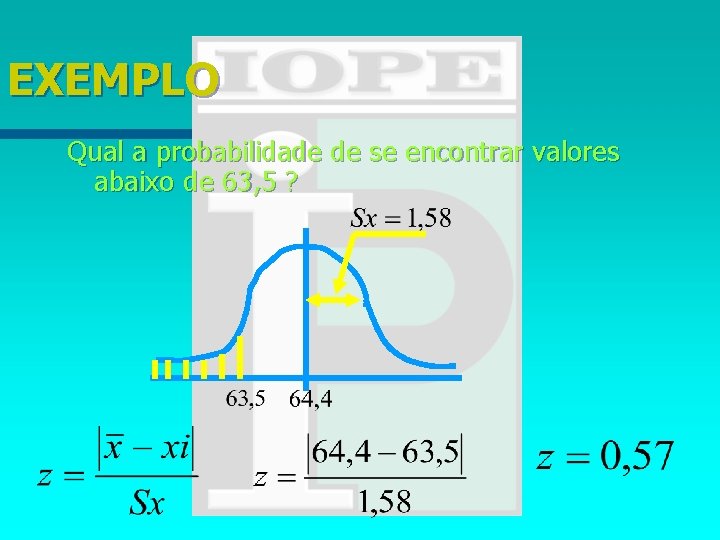
EXEMPLO Qual a probabilidade de se encontrar valores abaixo de 63, 5 ?

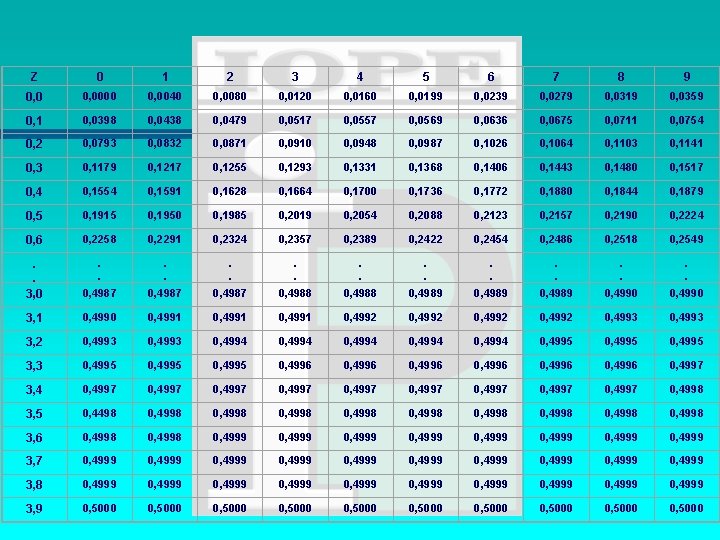
Z 0 1 2 3 4 5 6 7 8 9 0, 0000 0, 0040 0, 0080 0, 0120 0, 0160 0, 0199 0, 0239 0, 0279 0, 0319 0, 0359 0, 1 0, 0398 0, 0438 0, 0479 0, 0517 0, 0557 0, 0569 0, 0636 0, 0675 0, 0711 0, 0754 0, 2 0, 0793 0, 0832 0, 0871 0, 0910 0, 0948 0, 0987 0, 1026 0, 1064 0, 1103 0, 1141 0, 3 0, 1179 0, 1217 0, 1255 0, 1293 0, 1331 0, 1368 0, 1406 0, 1443 0, 1480 0, 1517 0, 4 0, 1554 0, 1591 0, 1628 0, 1664 0, 1700 0, 1736 0, 1772 0, 1880 0, 1844 0, 1879 0, 5 0, 1915 0, 1950 0, 1985 0, 2019 0, 2054 0, 2088 0, 2123 0, 2157 0, 2190 0, 2224 0, 6 0, 2258 0, 2291 0, 2324 0, 2357 0, 2389 0, 2422 0, 2454 0, 2486 0, 2518 0, 2549 . . . 3, 0 . . . 0, 4987 . . . 0, 4988 . . . 0, 4989 . . . 0, 4990 3, 1 0, 4990 0, 4991 0, 4992 0, 4993 3, 2 0, 4993 0, 4994 0, 4994 0, 4995 3, 3 0, 4995 0, 4996 0, 4996 0, 4997 3, 4 0, 4997 0, 4997 0, 4997 0, 4998 3, 5 0, 4498 0, 4998 0, 4998 0, 4998 3, 6 0, 4998 0, 4999 0, 4999 3, 7 0, 4999 0, 4999 0, 4999 3, 8 0, 4999 0, 4999 0, 4999 3, 9 0, 5000 0, 5000 0, 5000

CÁLCULO DE Z n Analisando a tabela encontramos para z = 0, 57 a probabilidade de 0, 2157 (21, 57%). Sendo o gráfico simétrico, pode-se dizer que cada lado da média corresponde a uma probabilidade de 50 % (0, 5), sendo assim, conclui-se que : n A probabilidade da faixa 63, 5 ~ 64, 4 : = 0, 5 – 0, 2157 = 0, 2843. n % Probabilidade abaixo de 63, 5 = 28, 43 %. n

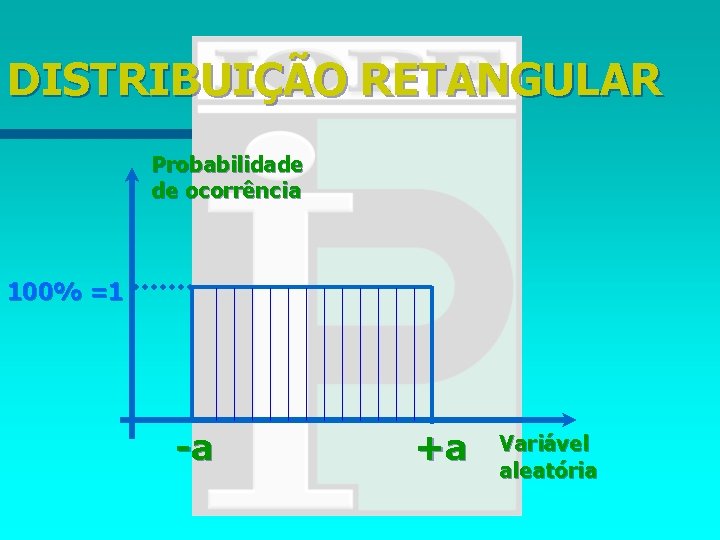
DISTRIBUIÇÃO RETANGULAR n Quando qualquer elemento do espaço amostral tem a mesma probabilidade de ocorrer e a distribuição tem distribuição contínua num intervalo -a ~ +a.

DISTRIBUIÇÃO RETANGULAR Probabilidade de ocorrência 100% =1 -a +a Variável aleatória

DISTRIBUIÇÃO RETANGULAR A integração desta distribuição resulta na seguinte expressão :

DISTRIBUIÇÃO RETANGULAR Se a diferença entre os limites, a+ - a-, é designada por 2 a, a equação : Quando não houver informações sobre o comportamento de uma variável aleatória adota-se uma distribuição retangular (2 a) pôr questão de segurança.

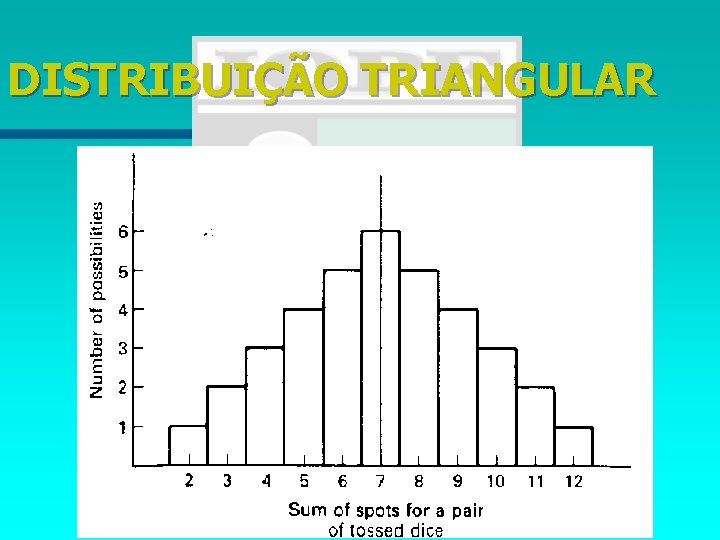
DISTRIBUIÇÃO TRIANGULAR n Nesta distribuição há maior probabilidade de ocorrer valores próximos a média, e ela decresce linearmente quando se afasta dela.

DISTRIBUIÇÃO TRIANGULAR

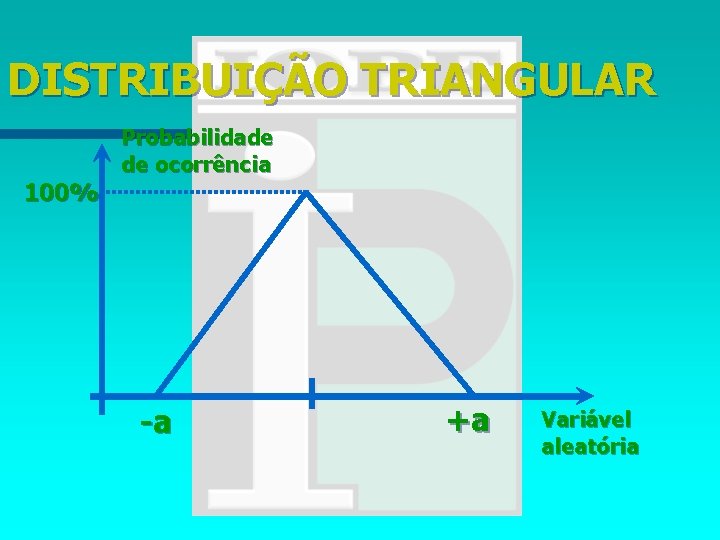
DISTRIBUIÇÃO TRIANGULAR Probabilidade de ocorrência 100% -a +a Variável aleatória

DISTRIBUIÇÃO TRIANGULAR A integração desta distribuição resulta na seguinte expressão :

DISTRIBUIÇÃO TRIANGULAR Se a diferença entre os limites, a+ - a-, é designada por 2 a, a equação:

DISTRIBUIÇÃO t-Student n. A medida que diminuímos o número de repetições, estamos também deixando de ter certeza de que a nossa amostra esteja representando exatamente uma distribuição Normal.

DISTRIBUIÇÃO t-Student n Para minimizar este inconveniente, foi desenvolvido por Willian S. Gosset, matematicamente a distribuição t, conhecida como a distribuição t de Student.

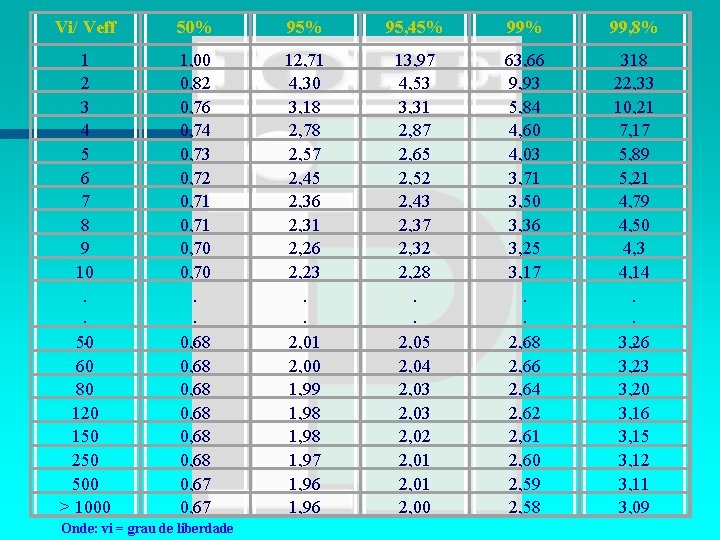
DISTRIBUIÇÃO t-Student Onde : t = valor tabelado em função do nível de confiança desejado e do grau de liberdade. = Número de medições para cada ponto; = Desvio padrão experimental.

Vi/ Veff 50% 95, 45% 99, 8% 1 2 3 4 5 6 7 8 9 10. . . 50 60 80 120 150 250 500 > 1000 1, 00 0, 82 0, 76 0, 74 0, 73 0, 72 0, 71 0, 70. . . 0, 68 0, 68 0, 67 12, 71 4, 30 3, 18 2, 78 2, 57 2, 45 2, 36 2, 31 2, 26 2, 23. . . 2, 01 2, 00 1, 99 1, 98 1, 97 1, 96 13, 97 4, 53 3, 31 2, 87 2, 65 2, 52 2, 43 2, 37 2, 32 2, 28. . . 2, 05 2, 04 2, 03 2, 02 2, 01 2, 00 63, 66 9, 93 5, 84 4, 60 4, 03 3, 71 3, 50 3, 36 3, 25 3, 17. . . 2, 68 2, 66 2, 64 2, 62 2, 61 2, 60 2, 59 2, 58 318 22, 33 10, 21 7, 17 5, 89 5, 21 4, 79 4, 50 4, 3 4, 14. . . 3, 26 3, 23 3, 20 3, 16 3, 15 3, 12 3, 11 3, 09 Onde: vi = grau de liberdade

OUTRAS DISTRIBUIÇÕES n. A redução contínua das incertezas de uma leitura nos leva a definir outros tipos de distribuição, mais próximo da real condição do ensaio.

OUTRAS DISTRIBUIÇÕES n Por este motivo, devemos procurar conhecer bem os efeitos aleatórios que envolvem o sistema de medição, para obtermos a forma gráfica mais próxima do ideal.

OUTRAS DISTRIBUIÇÕES Triangular : sendo a variância = Trapezoidal : sendo a variância = Para , então distribuição triangular. , então distribuição retangular. Existem também tipos como forma de U e outras, conforme análise estatística detalhada.

ERRO NORMATIZADO Dificilmente dois resultados de medição do mesmo mensurando dão o mesmo resultado. É necessário um critério para decidir se esses resultados são compatíveis. Quanto mais as incertezas forem menores mais os resultados devem ser próximos.

ERRO NORMATIZADO n Para esta situação utilizamos uma expressão matemática para critério de avaliação da compatibilidade entre os resultados de medição, critério adotado pelos laboratórios de referência para fins de acreditação de laboratórios de calibração.

ERRO NORMATIZADO Onde: = valor medido pelo laboratório avaliado; = valor medido pelo laboratório de referência; = incerteza expandida do laboratório avaliado; = incerteza expandida do laboratório de referência.

INCERTEZA DE MEDIÇÃO

INCERTEZA DE MEDIÇÃO n Quando se relata o resultado de medição, de uma grandeza física, é obrigatório que seja expressa alguma indicação quantitativa da qualidade do resultado, de forma tal, que aqueles que o utilizam possam avaliar sua confiabilidade.

INCERTEZA DE MEDIÇÃO n Os fundamentos metodológicos para o cálculo de incerteza de medição são procedimentos puramente estatísticos, sendo descrito detalhadamente no guia conhecido mundialmente como ISO GUM “Guia para Expressão da Incerteza de Medição”.

INCERTEZA DE MEDIÇÃO n Posteriormente a European Cooperation for Accreditation (Cooperação Européia para Acreditação) desenvolveu um documento que resume a metodologia do ISO GUM e sua aplicação com exercícios (EA 4/02).

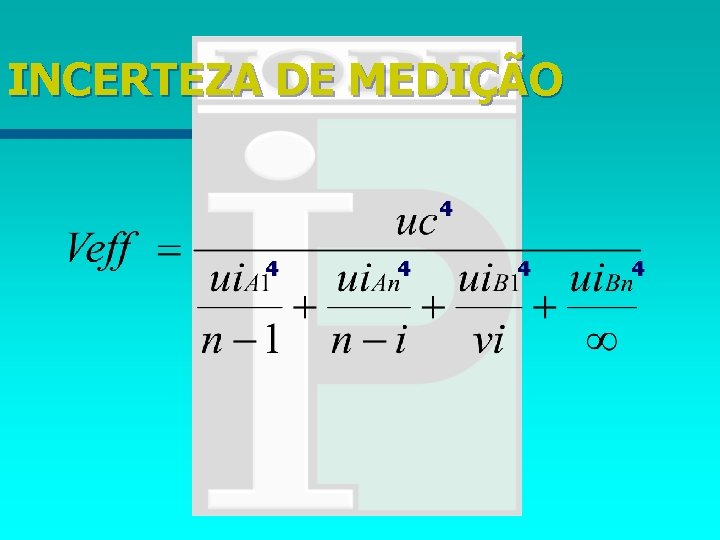
FÓRMULA PADRÃO DA INCERTEZA DE MEDIÇÃO

INCERTEZA DE MEDIÇÃO Equação : U = incerteza de medição; k = intervalo de confiança; n = número de estimativas da incerteza de medição; ci = coeficiente de sensibilidade utilizado para transformar estimativas de entrada em estimativas de saída; u(xi) = incerteza padrão de entrada.

INCERTEZA DE MEDIÇÃO ESTIMATIVA DE ENTRADA - u(xi) Para se calcular uma incerteza de medição, primeiramente deve-se conhecer o processo de medição e definir quais são as estimativas de entrada, que interferem no resultado final da leitura. Ex. repetitividade, resolução, deriva, instabilidade, temperatura ambiente, etc.

INCERTEZA DE MEDIÇÃO n Definir para cada estimativa, qual a sua contribuição, ou seja, qual o intervalo de dúvida desta estimativa (+a ~ -a). n Transformar este intervalo de dúvida em um desvio padrão de entrada (u(xi)), dividindo o intervalo (+a ~ -a) pelo fator que define a probabilidade do intervalo, em função do tipo de distribuição, o qual o intervalo representa (divisor) :

INCERTEZA DE MEDIÇÃO n Para definirmos os desvios padrões de entrada u(xi), devemos conhecer melhor as distribuições de probabilidade das estimativas, as quais subdividimos em dois tipos: n incerteza tipo A e incerteza tipo B.

INCERTEZA DE MEDIÇÃO INCERTEZA TIPO A n Parcelas que são avaliadas por meio de métodos estatísticos. nÉ caracterizada como uma parcela de incerteza padrão de repetitividade ( (Distribuição Normal). )

INCERTEZA DE MEDIÇÃO n Uma série de medidas, obtidas sob condição de repetitividade, pode apresentar uma dispersão de seus valores individuais. n Neste caso, a incerteza padrão é o desvio padrão experimental médio que possui sua distribuição normal.

INCERTEZA DE MEDIÇÃO INCERTEZA TIPO B São parcelas que são avaliadas por outros métodos não estatísticos. Estas parcelas estão ligadas a : - Resolução do equipamento; - Incerteza dos padrões utilizados na calibração; - Influências externas (condições ambientais, estabilidade, deriva, etc. ).

INCERTEZA DE MEDIÇÃO Exemplo : - Parcela de incerteza padrão da incerteza de medição (I. M. ) do padrão. – Distribuição Normal. k = fator de abrangência do certificado do padrão.

INCERTEZA DE MEDIÇÃO EXEMPLO : Se durante uma calibração foi utilizado um calibrador padrão microprocessado para calibrar um indicador de temperatura, e este padrão possui uma incerteza de medição indicada em seu certificado no valor de: Nota : Quando for utilizado mais de um padrão, devese calcular um a um conforme indicado acima.

INCERTEZA DE MEDIÇÃO n Incerteza padrão em que se utiliza a distribuição retangular. n Parcela de incerteza padrão que se utiliza todo o intervalo no cálculo (ex. resolução de um indicador digital).

INCERTEZA DE MEDIÇÃO Se estivermos lendo no equipamento 1, 0 mm, sendo este digital e com valor de uma divisão 1, 0 mm, é impossível se interpolar valores intermediários, observaremos que ele indicará 1, 0 mm para valores entre 0, 5 e 1, 5 mm, só a partir daí indicará 2, 0 mm até que o valor verdadeiro ultrapasse 2, 5 mm, ou seja, sempre teremos um erro, ou melhor, uma incerteza para os valores. 2, 0 4, 0 0, 0 1, 0 3, 0 5, 0

INCERTEZA DE MEDIÇÃO A incerteza pertence ao intervalo de indicação. Incerteza da Resolução :

INCERTEZA DE MEDIÇÃO O desvio padrão da resolução no cálculo da incerteza de medição será do equipamento que varia durante a calibração, podendo ser do equipamento que está sendo calibrado ou do padrão, ou dos dois, (neste caso deve-se calcular um a um).

INCERTEZA DE MEDIÇÃO Exemplo: Considerando o exemplo anterior, possui uma resolução de 1 mm. mm

INCERTEZA DE MEDIÇÃO Parcela de incerteza padrão que utiliza o intervalo bilateral no cálculo (ex. deriva). A deriva pode ser a mudança do erro do padrão da última calibração para a atual, sendo que neste caso a mudança pode ser para mais ou para menos.

INCERTEZA DE MEDIÇÃO Exemplo : Considerando que a mudança do erro de um padrão foi de +0, 03°C, desde da última calibração, temos: ºC

INCERTEZA DE MEDIÇÃO Parcelas de incerteza padrão em que se utiliza outro tipo de distribuição. z = divisor utilizado para transformar a dúvida em um desvio padrão. Ex. para triangular z=6, para tipo U z=2.

INCERTEZA DE MEDIÇÃO INCERTEZA PADRÃO (U): É a incerteza do resultado de uma medição expressa como um desvio padrão.

INCERTEZA DE MEDIÇÃO COEFICIENTE DE SENSIBILIDADE (ci) n. O coeficiente de sensibilidade é um coeficiente que tem a função de expressar o quanto à estimativa de saída (y) varia em função da estimativa de entrada (xi). n Utiliza-se também o ci para transformação de unidade.

INCERTEZA DE MEDIÇÃO Ci = Derivada parcial da função f em relação à variável Xi. Se a estimativa de entrada for a mesma grandeza da saída ci = 1.

INCERTEZA DE MEDIÇÃO n Ci é um coeficiente de transformação da estimativa de entrada, qual possua uma grandeza diferente da grandeza da estimativa de saída.

INCERTEZA DE MEDIÇÃO Exemplo : Se tivermos uma estimativa de entrada em ohms (de uma termoresistência) e a estimativa de saída deverá ser em graus Celsius, calculamos : 1°C = 0, 385 Ohm o 1 ohm = 2, 597°C

INCERTEZA DE MEDIÇÃO INCERTEZA PADRÃO COMBINADA (Uc) É a combinação das incertezas padrão. Sendo igual à raiz quadrada de uma soma de termos, sendo estes, as variâncias de grandezas ponderadas, de acordo com suas distribuições. 2 2 2

INCERTEZA DE MEDIÇÃO FATOR DE ABRANGENCIA k Para a incerteza de medição devemos calcular o fator de abrangência, para estimar uma probabilidade (geralmente na faixa de 95 % ~ 99, 8%). Para isto devemos calcular o Veff. 4 4

INCERTEZA DE MEDIÇÃO 4 4 4

INCERTEZA DE MEDIÇÃO Se Veff for maior que 1000, considera-se o resultado como uma distribuição de probabilidade Normal e utiliza-se k= 2, 00 para uma probabilidade de abrangência de 95, 45%. Valor obtido pela tabela t de Student. No exel =invt(0, 0455; valor de Veff).

NÍVEL DE CONFIANÇA

INCERTEZA DE MEDIÇÃO n. A incerteza de medição deve ser declarada na mesma unidade da estimativa “y” ou e em percentagem da seguinte forma : Y ± U(% ou unidade)

INCERTEZA DE MEDIÇÃO INCERTEZA EXPANDIDA (U): Grandeza que define um intervalo em torno do resultado de uma medição que pode ser esperado em englobar uma grande fração da distribuição de valores que podem ser razoavelmente atribuídos ao mensurando.

INCERTEZA DE MEDIÇÃO INCERTEZA EXPANDIDA (U): Notas: 1) A fração pode ser vista como a probabilidade de abrangência ou nível de confiança do intervalo.

INCERTEZA DE MEDIÇÃO INCERTEZA EXPANDIDA (U): 2) Para associar um nível de confiança específico ao intervalo definido pela incerteza expandida, são necessárias suposições explícitas ou implícitas com respeito à distribuição de probabilidade caracterizada pelo resultado da medição e sua incerteza combinada.

INCERTEZA DE MEDIÇÃO INCERTEZA EXPANDIDA (U): O nível de confiança que pode ser atribuído a este intervalo só pode ser conhecido na medida em que tais suposições possam ser justificadas.

INCERTEZA DE MEDIÇÃO n. O certificado ou relatório deve conter uma nota dizendo : n “A incerteza expandida de medição relatada é declarada como a incerteza padrão da medição multiplicada pelo fator de abrangência k= xx, que para uma distribuição normal corresponde a uma probabilidade de abrangência de 95, 45%”.

Procedimento para a determinação da incerteza de medição Determinar o modelo matemático que relaciona a grandeza 1. de entrada com a de saída y=f(x 1, x 2, x 3, . . . , xn) 2. Identificar todas as correções a serem feitas ao resultado de medição; 3. Listar componentes sistemáticos da incerteza associada a correções e tratar efeitos sistemáticos não corrigidos como parcelas de incerteza; 4. Atribuir valores de incerteza e distribuição de probabilidade com base em conhecimentos experimentais práticos ou teóricos; 5. Calcular a Incerteza Padrão (ui) para cada componente de incerteza; 6. Calcular a Incerteza Combinada (uc); 7. Calcular a Incerteza Expandida (U).

EXEMPLO MEDIÇÃO DE RESISTÊNCIA ELÉTRICA. -Um multímetro digital foi utilizado para medir uma resistência elétrica de 138, 5 ohms. Determinar a componente tipo A da incerteza, considerando 5 medições de resistência, obtidas com o multímetro.

EXEMPLO Valores medidos (ohms) 138, 5243 138, 5279 138, 5298 138, 5217

EXEMPLO

EXEMPLO As incertezas tipo B foram obtidas do certificado de calibração do multímetro, do manual do fabricante e de dados experimentais. As incertezas e distribuições de probabilidade assumidas são as seguintes:

EXEMPLO Distribuição Tipo B FONTES DE INCERTEZA VALOR (Ohms) DISTRIBUIÇÃO ASSUMIDA INCERTEZA DO MULTÍMETRO 0, 08 NORMAL (k=2, 02) DESVIO TEMPORAL 0, 015 RETANGULAR RESOLUÇÃO DO MULTÍMETRO 0, 01 RETANGULAR

EXEMPLO 2 2 =incerteza de repetitividade; =incerteza da calibração do multímetro; =incerteza do desvio temporal; =incerteza da resolução.

EXEMPLO 2 2

EXEMPLO INCERTEZA EXPANDIDA 4 4 4

EXEMPLO Incerteza expandida : Resultado da medição :

ESTRUTURA DE PLANILHA PARA INCERTEZA DE MEDIÇÃO

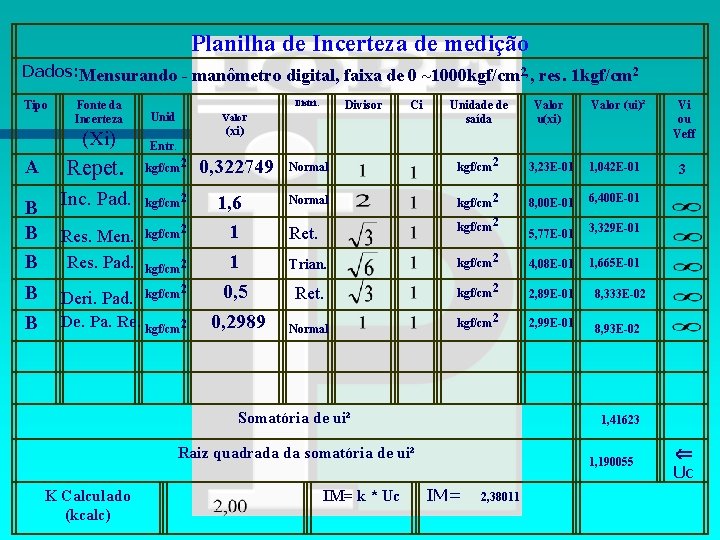
EXEMPLO Calibracão de um manômetro de Bourdon (0 ~ 1000 kgf/cm 2), dados : -Repetitividade = 0, 322749 kgf/cm 2; -Incerteza da calibração do padrão =1, 6 kgf/cm 2; -Resolução do mensurando = 1 kgf/cm 2; -Resolução do padrão = 1 kgf/cm 2; -Desvio temporal do padrão = 0, 5 kgf/cm 2; -Desvio padrão residual do padrão = 0, 2989 kgf/cm 2;

Planilha de Incerteza de medição Dados: Mensurando - manômetro digital, faixa de 0 ~1000 kgf/cm 2, , res. 1 kgf/cm 2 Tipo A B B B Fonte da Incerteza Unid (Xi) Entr. Divisor 0, 322749 Normal 2 kgf/cm Normal kgf/cm 2 Ret. 2 kgf/cm Trian. kgf/cm 2 4, 08 E-01 Ret. 2 kgf/cm 2, 89 E-01 2 kgf/cm 2, 99 E-01 Valor (xi) Repet. 2 kgf/cm Inc. Pad. kgf/cm 2 Res. Men. Res. Pad. kgf/cm 2 Deri. Pad. Distri. kgf/cm 2 De. Pa. Re. kgf/cm 2 1, 6 1 1 0, 5 0, 2989 Normal Ci Unidade de saída Valor u(xi) 3, 23 E-01 Valor (ui)² Vi ou Veff 1, 042 E-01 3 6, 400 E-01 3, 329 E-01 1, 665 E-01 8, 00 E-01 5, 77 E-01 8, 333 E-02 8, 93 E-02 Uc Somatória de ui² 1, 41623 Raiz quadrada da somatória de ui² K Calculado (kcalc) IM= k * Uc 1, 190055 IM= 2, 38011

FONTES DE INCERTEZA

Área: Dimensional -Incerteza do SM ou Padrão de referência (certificado de calibração) ; -Estabilidade do SM/Padrão em função do tempo, (grau de utilização/agressividade do meio); - Resolução; -Influência das condições ambientais sobre o SM; -Efeitos de temperatura sobre o mesurando; -Deformação elástica; -Erros de coseno; -Erros geométricos.

Área: Massa n Incerteza do Padrão de referência (certificado de calibração); n Estabilidade dos valores de massa em função do tempo; n Processo de medição/comparador/ balança : n Repetitividade ; n Resolução; n Linearidade; n Efeitos de temperatura.

Área: Massa n Erros nos comprimentos dos braços; n Empuxo do ar; n Condições Ambientais : n Gradientes de temperatura; n Umidade; n Mudança de temperatura na sala; n Contaminação de partículas;

Área: Pressão n Incerteza do SM ou Padrão de referência (certificado de calibração); n Resolução do Padrão; n Resolução do Instrumento de medição; n Peso específico de um fluído; n Temperatura ambiente; n Incerteza da gravidade local; n Incerteza da área do pistão;

Área : Temperatura n n n n n Incerteza do Padrão de referência (certificado de calibração); Estabilidade em função do tempo; Equipamentos (padrão de tensão ou resistência) e instrumentos de medições envolvidos; Auto- aquecimento (termoresistência); Fios de compensação e juntas de referências; Estabilidade térmica do mensurado; Imersão parcial/efeitos de colunas emergentes; Incerteza dos meios térmicos; Interpolação matemática (tabelas de referência e ajustes de curvas).

Área : Elétrica n n n n n Incerteza do SM ou Padrão de referência (certificado de calibração); Estabilidade do SM em funções do tempo; Estabilidade do SM em Função das condições de uso; Resolução; Interpolação de dados de calibração; Interligação dos vários módulos do SM; Tensões termoelétricas ; Eleitos de impedância; Repetitividade devido à conexão de condutores elétricos.

FONTES DE INCERTEZAS COMUNS A TODAS AS ÁREAS 1 - Incerteza do SM ou Padrão; 2 - Condições Ambientais; 3 - Repetitividade (tipo A ); 4 - Erros matemáticos; 5 - Aproximação; 6 -Ajuste de curva e interpolação em tabelas; 7 - Erros de arredondamento/truncamento; Ex: 2, 346 = 2, 35 = 2, 4 2, 346 = 2, 3