2 DISTRIBUCIN NORMAL MULTIVARIANTE Introduccin Normal bivariante Normal

2. DISTRIBUCIÓN NORMAL MULTIVARIANTE § Introducción § Normal bivariante § Normal multivariante § Distribución 2 § Muestreo en poblaciones normales § Distribución de Wishart § Lema de Fisher multivariante § Teorema central del límite 1

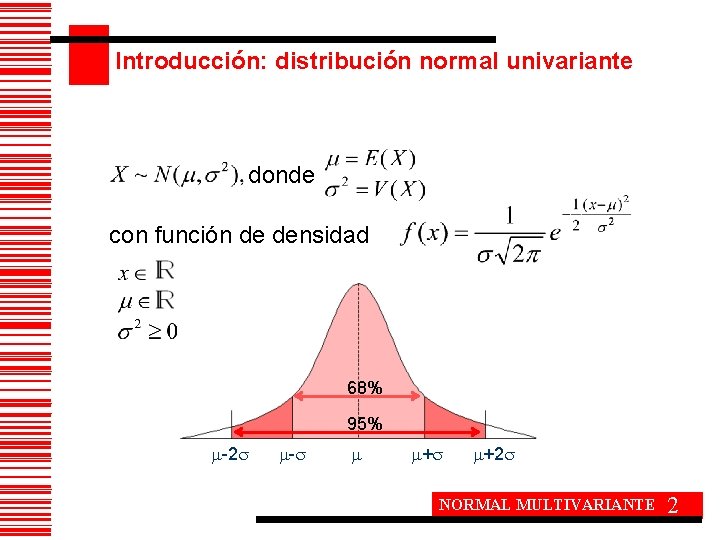
Introducción: distribución normal univariante donde con función de densidad 68% 95% -2 - + +2 NORMAL MULTIVARIANTE 2

Normal multivariante donde con función de densidad: NORMAL MULTIVARIANTE 3

Normal bivariante Ejemplo Desarrollar NORMAL MULTIVARIANTE 4

Normal bivariante donde con función de densidad NORMAL MULTIVARIANTE 5

EJEMPLOS 6

EJEMPLOS 7

Normal bivariante Propiedades § 12 =0 f(x 1 , x 2)=f(x 1)f(x 2) X 1, X 2 independientes § ( , e) autovalor y autovector de (1/ , e) autovalor y autovector de -1 NORMAL MULTIVARIANTE 8

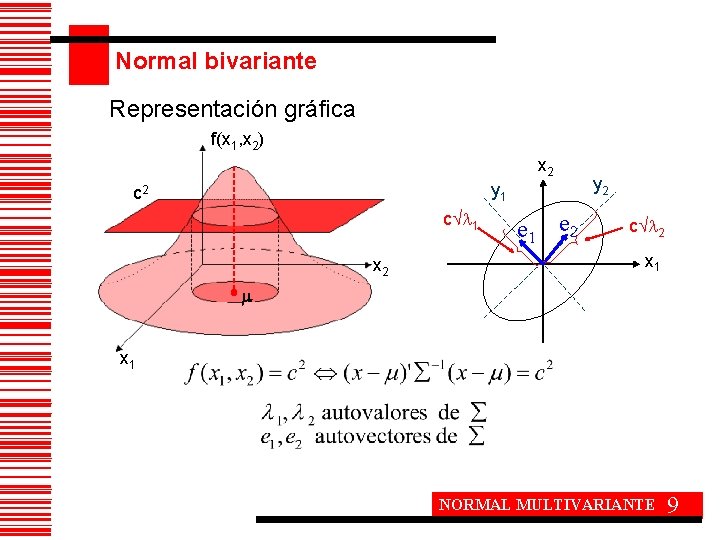
Normal bivariante Representación gráfica f(x 1, x 2) x 2 y 1 c 2 c 1 x 2 e 1 e 2 y 2 c 2 x 1 NORMAL MULTIVARIANTE 9

Normal bivariante Ejemplo Hallar las elipses de densidad constante para NORMAL MULTIVARIANTE 10

Normal multivariante Propiedades NORMAL MULTIVARIANTE 11

Normal multivariante NORMAL MULTIVARIANTE 12

Normal multivariante NORMAL MULTIVARIANTE 13

Normal multivariante NORMAL MULTIVARIANTE 14

Normal multivariante Ejemplo NORMAL MULTIVARIANTE 15

Normal multivariante NORMAL MULTIVARIANTE 16

Normal multivariante NORMAL MULTIVARIANTE 17

Normal multivariante Ejemplo Dada (X 1, X 2), obtener la distribución de X 2 condicionada por X 1 =x 1 NORMAL MULTIVARIANTE 18

Normal multivariante (vii) Distribución de combinación lineal de normales NORMAL MULTIVARIANTE 19

Normal multivariante (viii) Distribución conjunta de normales NORMAL MULTIVARIANTE 20

Normal multivariante Ejemplo NORMAL MULTIVARIANTE 21

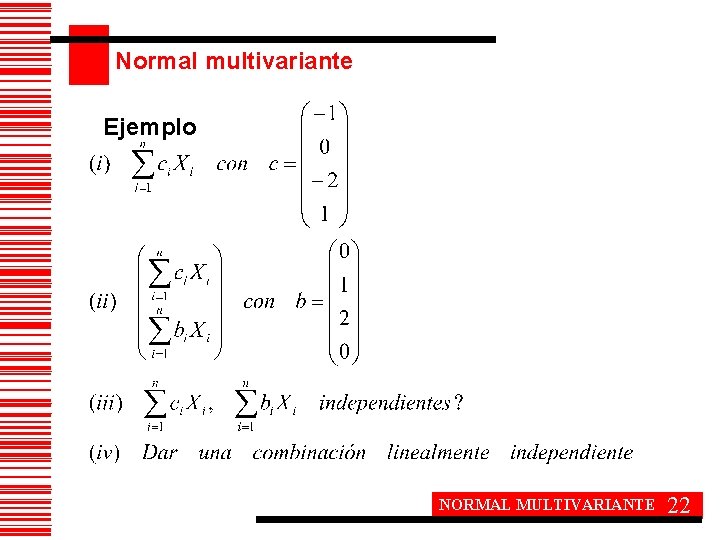
Normal multivariante Ejemplo NORMAL MULTIVARIANTE 22

Distribución 2 NORMAL MULTIVARIANTE 23

Distribución 2 Propiedades 2 p, NORMAL MULTIVARIANTE 24

Muestreo en poblaciones normales Estimadores de máxima verosimilitud para y NORMAL MULTIVARIANTE 25

Muestreo en poblaciones normales Derivando parcialmente con respecto a todas las variables e igualando a cero, se obtiene: NORMAL MULTIVARIANTE 26

Muestreo en poblaciones normales Propiedades estadísticos suficientes para En una dimensión, son normales independientes NORMAL MULTIVARIANTE 27

Distribución de Wishart independientes, Wishart con m grados de libertad Propiedades NORMAL MULTIVARIANTE 28

Lema de Fisher multivariante son independientes NORMAL MULTIVARIANTE 29

Teorema Central del Límite (i) es asintóticamente normal d (ii) es consistente: (iii) (iv) c. s. n P n d n NORMAL MULTIVARIANTE 30