KURVE NORMAL KURVE NORMAL Distribusi Normal Suatu alat
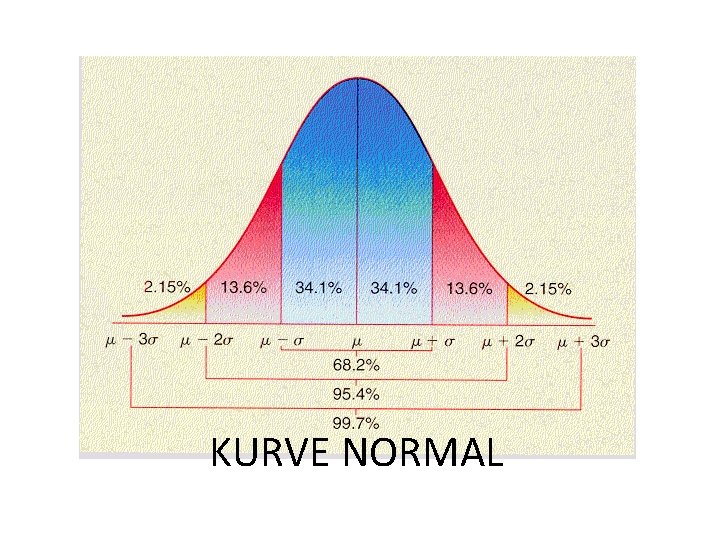
KURVE NORMAL
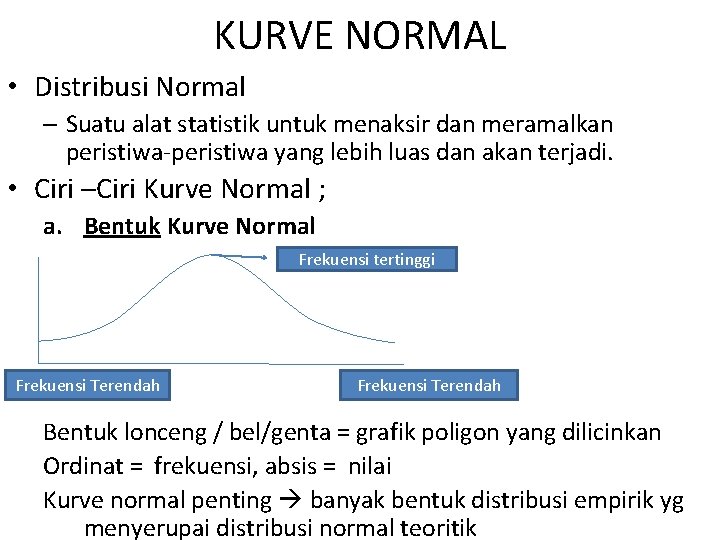
KURVE NORMAL • Distribusi Normal – Suatu alat statistik untuk menaksir dan meramalkan peristiwa-peristiwa yang lebih luas dan akan terjadi. • Ciri –Ciri Kurve Normal ; a. Bentuk Kurve Normal Frekuensi tertinggi Frekuensi Terendah Bentuk lonceng / bel/genta = grafik poligon yang dilicinkan Ordinat = frekuensi, absis = nilai Kurve normal penting banyak bentuk distribusi empirik yg menyerupai distribusi normal teoritik

b. Daerah Kurve Normal 100 % MEAN • Mean : terletak ditengah grafik kurve Normal • Dibagi menjadi 6 SD (standar Deviasi) • Disebelah kanan Mean : + 1 SD, + 2 SD, +3 SD • Disebelah kiri mean : - 1 SD, -2 SD, -3 SD • Jarak setiap SD sama
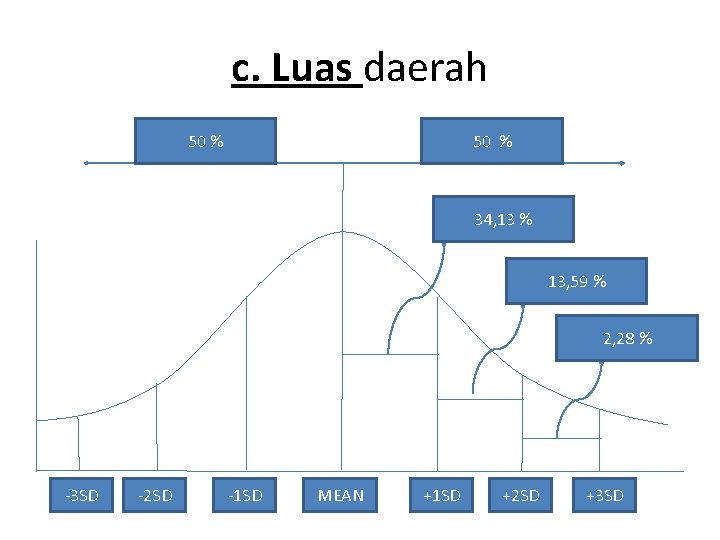
c. Luas daerah 50 % 34, 13 % 13, 59 % 2, 28 % -3 SD -2 SD -1 SD MEAN +1 SD +2 SD +3 SD

Contoh 1 • Diteliti berat badan 10. 000 orang di Jawa tengah, diperoleh Mean berat badan = 50 kg dan SD = 10 Kg. Berapa orang yang mempunyai berat badan antara 50 kg s/d 60 kg?
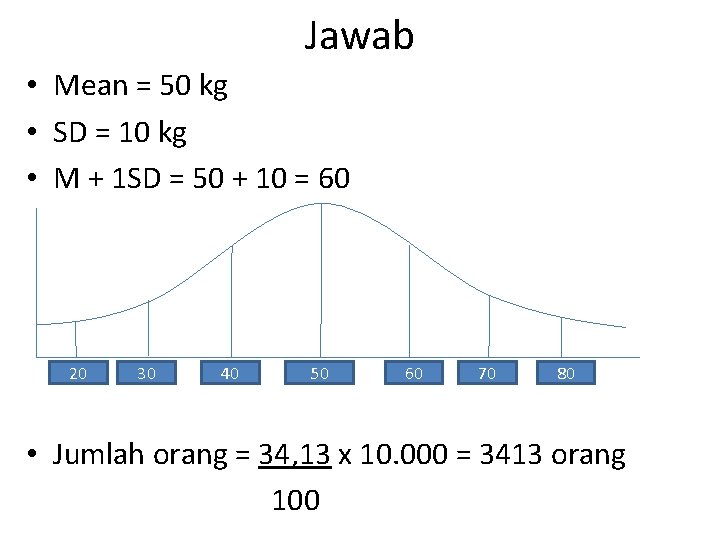
Jawab • Mean = 50 kg • SD = 10 kg • M + 1 SD = 50 + 10 = 60 20 30 40 50 60 70 80 • Jumlah orang = 34, 13 x 10. 000 = 3413 orang 100

Tabel Kurve Normal • z = deviasi-deviasi dari mean dalam satuan SD X= deviasi suatu nilai dari M M=mean, rerata x= X-M Tabel Kurve normal hanya memberikan persentase setinggi-tingginya 50 % tabel ini hanya mencantumkan daerah di sebelah kurve sebelah kanan kurve atau sebelah kiri saja. kurve norma berbentuk simetris • Satuan kurve normal z score • Satuan Distribusi empirik kg, cm, liter, dll perlu di ubah dengan tabel kurve Normal. • •

Contoh 2 • Diteliti terhadap 300 orang atlit peloncat tinggi, di dapat Mean = 160 cm, SD=13 cm. Berapa orang yang dapat meloncat 180 cm ke atas? • Jawab : – Penyimpangan 180 cm - 160 cm = 20 cm – SD = 13 cm – Zcore = 20/13 = +1, 54 penyimpangan angka kasar – Tanda + menunjukkan di sebelah kanan mean. – Cara melihat tabel kurve Normal lihat z score nya
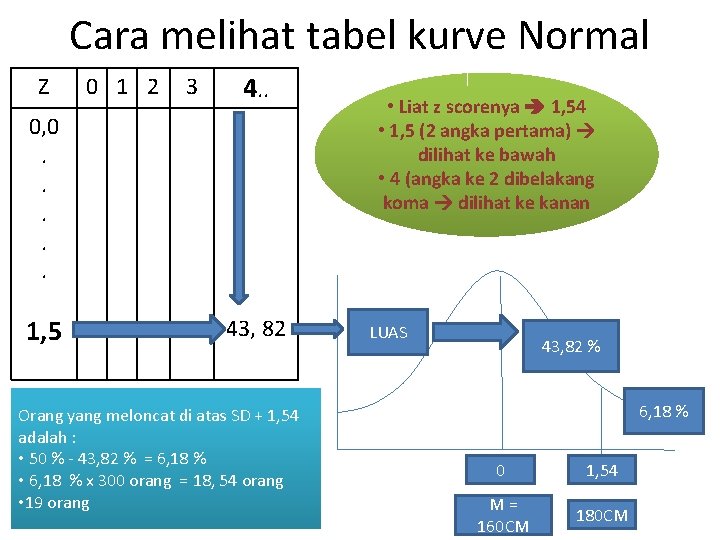
Cara melihat tabel kurve Normal Z 0 1 2 3 4. . 0, 0. . . 1, 5 43, 82 Orang yang meloncat di atas SD + 1, 54 adalah : • 50 % - 43, 82 % = 6, 18 % • 6, 18 % x 300 orang = 18, 54 orang • 19 orang • Liat z scorenya 1, 54 • 1, 5 (2 angka pertama) dilihat ke bawah • 4 (angka ke 2 dibelakang koma dilihat ke kanan LUAS 43, 82 % 6, 18 % 0 1, 54 M= 160 CM 180 CM

Pertanyaan selanjutnya • Berapa proporsi orang yang tidak dapat meloncat setinggi 140 cm? ? ? • Jawab : – M = 160 cm ; SD = 13 ; N = 300 – Penyimpangan 140 cm = 140 cm – 160 cm = -20 cm – - 20 cm di bawah mean – Zscore = -20 / 13 = - 1, 54 tabel 43, 82 % – Proporsinya = 50 % - 43, 82 % = 6, 18 % = 0, 0618 – Yang dapat meloncat 6, 18 % x 300 orang = 18, 54 = 19 orang

Soal • Disebuah sekolah di dapat hasil tes prestasi akademik dari 200 siswa, di dapat mean sebesar 75 dan SD = 9 – Berapakah orang yang mendapat nilai 85 ke atas ? – Berapakah orang yang mendapat nilai 60 ke bawah ?

Contoh Soal 3 • Atlit yang dikualifikasikan ke dalam golongan 10 % adalah peloncat tertinggi yang dapat meloncat. Berapa cm kah tinggi loncatannya? (Mean = 160 cm, SD = 13, N= 300) • Jawab : – Cari luas kurve normal dari M 50 % - 10 % = 40 % 10 % 40% M Z SD = 1, 28 ; 1 SD = 13 cm 1, 28 x 13 cm = + 16, 64 cm Mean + SD 1, 28 = 160 cm + 16, 64 cm = 176, 64 cm Tabel = 39, 9 % Zscore = 1, 28

Pertanyaan lanjutan. . . • Berapakah tinggi loncatan-loncatan yang hanya dapat dicapai dengan 5 % dari kelompok tersebut? ? (Mean = 160 cm, SD = 13, N= 300) • Jawab : – Zscore= + 1, 96 – + 1, 96 x 13 = + 25, 48 cm – Loncatan tertinggi = 160 + 25, 48 cm = 185, 48 cm – Loncatan terendah = 160 - 25, 48 cm = 134, 52 cm
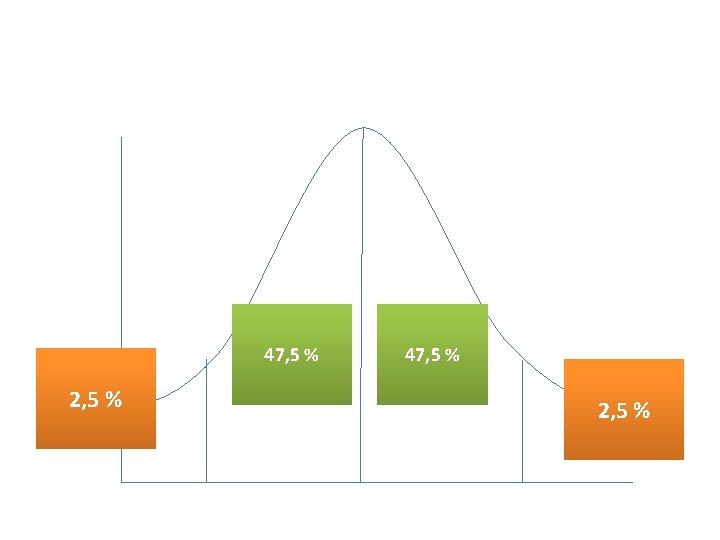
47, 5 % 2, 5 %

Soal • Diteliti tentang kemampuan membaca pada anak SD sebanyak 500 siswa, didapat hasil bahwa kemampuan rata-rata membaca siswa kelas 1 adalah sebesar 75, dan SD = 10. berapa nilai membaca siswa yg dapat digolongkan dalam 20 % terbaik?
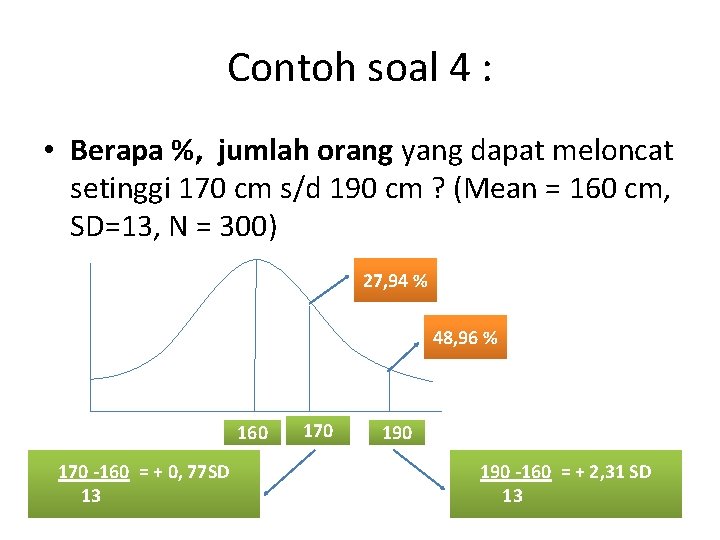
Contoh soal 4 : • Berapa %, jumlah orang yang dapat meloncat setinggi 170 cm s/d 190 cm ? (Mean = 160 cm, SD=13, N = 300) 27, 94 % 48, 96 % 160 170 -160 = + 0, 77 SD 13 170 190 -160 = + 2, 31 SD 13

• • + 2, 31 SD = 48, 96 % +0, 77 SD = 27, 94 % Luas = 48, 96 % - 27, 94 % = 21, 02 % Jumlah orang = 21, 02 % x 300 orang = 63, 06 orang = 63 orang

Soal • Apabila diketahui jumlah orang 200, dengan nilai rata-rata kecepatan naik kendaraan di tol sebesar 75 km/jam dan SD = 9 – Berapa % dan berapa jumlah orang yang naik kendaraan dengan kecepatan antara 80 – 90 km/jam – Berapa % dan berapa jumlah orang yang naik kendaraan dengan kecepatan antara 45 – 50 km/jam
- Slides: 18