La statica degli archi in muratura Terminologia degli

La statica degli archi in muratura

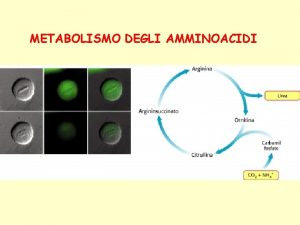
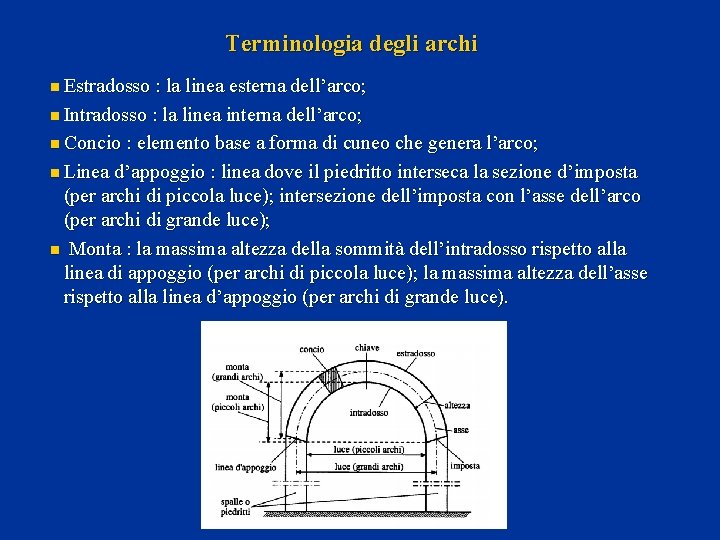
Terminologia degli archi n n n Asse : linea media dell’arco; Sesto : la forma dell’asse dell’arco; Imposta : la sezione in cui l’arco si appoggia alla spalla o al piedritto; Chiave : il punto più alto dell’arco; Altezza : la lunghezza del segmento perpendicolare alla tangente all’asse; Luce : la dimensione orizzontale fra le spalle o i piedritti (per archi di piccola luce coincide con la luce netta della apertura; per archi di grande luce coincide con la distanza presa fra le due intersezioni dell’asse con le imposte);

Terminologia degli archi n Estradosso : la linea esterna dell’arco; n Intradosso : la linea interna dell’arco; n Concio : elemento base a forma di cuneo che genera l’arco; n Linea d’appoggio : linea dove il piedritto interseca la sezione d’imposta (per archi di piccola luce); intersezione dell’imposta con l’asse dell’arco (per archi di grande luce); n Monta : la massima altezza della sommità dell’intradosso rispetto alla linea di appoggio (per archi di piccola luce); la massima altezza dell’asse rispetto alla linea d’appoggio (per archi di grande luce).

Cenni storici Una prima teoria statica dell’arco fu stabilita solo alla fine del XVII secolo. In epoca precedente si ebbero solo alcuni tentativi anche se i costruttori medievali avevano un metodo geometrico empirico per dimensionare i piedritti al fine di contenere la spinta dell’arco. Dividendo l’arco, sia che fosse a tutto sesto, sia a sesto acuto, in tre parti eguali, AB, BC, CD, con centro in D e raggio CD si descriveva una semicirconferenza. L’estremità del diametro opposta a C, E, apparteneva al filo esterno del piedritto. La regola conduce ad avere piedritti di spessore maggiore per archi a tutto sesto che per archi a sesto acuto, poiché maggiore è la spinta.

Solo Leonardo da Vinci (secolo XV) fornì i primi spunti di corretta interpretazione meccanica del comportamento di un arco affermando nel manoscritto del Codice Foster: Arco non è altro che una fortezza causata da due debolezze, imperoché l’arco negli edifizi è composto di due quarti di circulo, i quali quarti circuli, ciascuno debolissimo per sé, desidera cadere e oponendosi alla ruina l’uno dell’altro, le due debolezze si convertono in una unica fortezza. Leonardo sperimentò anche un metodo per la verifica al ribaltamento degli archi, stabilendo una condizione secondo la quale le sezioni dell’arco non ruotano: l’arco è assimilato a due barre rettilinee, ab e bc e si afferma che: L’arco non si romperà se la corda dell’archi di fori non tocherà l’arco di dentro. Ciò dimostra l’intuizione della condizione che la curva delle pressioni risulti interna all’arco.

Le teorie statiche dell'arco: Philippe De LA HIRE (1640 -1718) I primi contributi significativi alla teoria statica dell'arco sono dovuti a De La Hire. L'arco viene studiato come una macchina semplice in grado di spiegare l'equilibrio. I conci vengono intesi come porzioni di cunei insistenti su letti di malta. Il modello non è soddisfacente ma ha il merito di costituire il primo approccio meccanico agli archi e di avere considerato le strutture in muratura come sistemi rigidi, dotati di peso. Le ipotesi di base: • assenza di deformabilità: effettivamente trascurabile in prima approssimazione • assenza di attrito: è invece un aspetto importante ed è l'aspetto per il quale la teoria entra in contraddizione

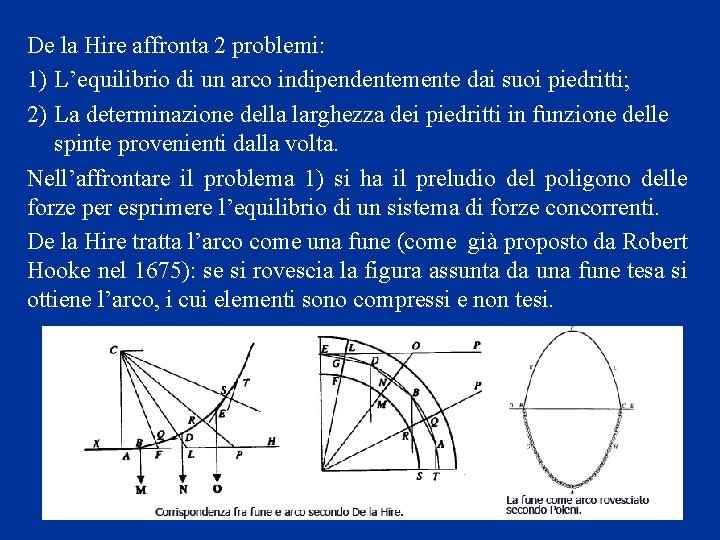
De la Hire affronta 2 problemi: 1) L’equilibrio di un arco indipendentemente dai suoi piedritti; 2) La determinazione della larghezza dei piedritti in funzione delle spinte provenienti dalla volta. Nell’affrontare il problema 1) si ha il preludio del poligono delle forze per esprimere l’equilibrio di un sistema di forze concorrenti. De la Hire tratta l’arco come una fune (come già proposto da Robert Hooke nel 1675): se si rovescia la figura assunta da una fune tesa si ottiene l’arco, i cui elementi sono compressi e non tesi.

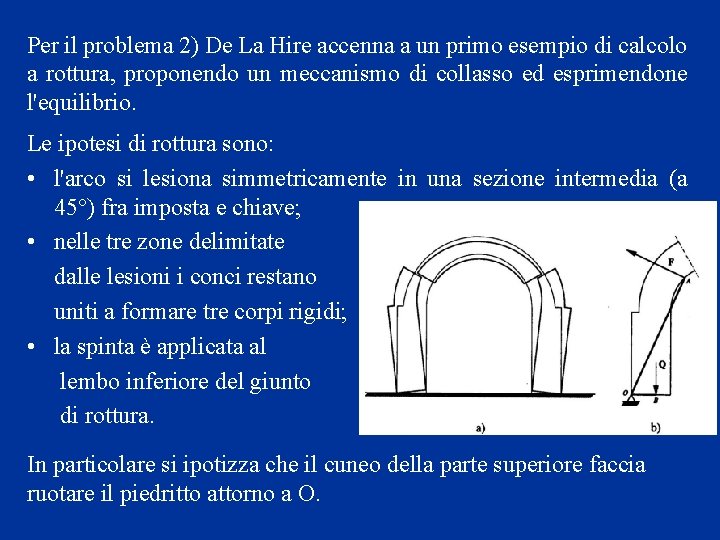
Per il problema 2) De La Hire accenna a un primo esempio di calcolo a rottura, proponendo un meccanismo di collasso ed esprimendone l'equilibrio. Le ipotesi di rottura sono: • l'arco si lesiona simmetricamente in una sezione intermedia (a 45°) fra imposta e chiave; • nelle tre zone delimitate dalle lesioni i conci restano uniti a formare tre corpi rigidi; • la spinta è applicata al lembo inferiore del giunto di rottura. In particolare si ipotizza che il cuneo della parte superiore faccia ruotare il piedritto attorno a O.

Il procedimento non è del tutto errato. Limiti del modello: • Il meccanismo considerato (scorrimento verso il basso del cuneo centrale) è possibile ma non molto probabile; • L'assenza di attrito (ipotesi che è contraddetta già dai risultati del modello); • La componente F della forza esercitata dal concio centrale risulta perpendicolare alla leva nel punto A; • Il contributo stabilizzante (peso del cuneo inferiore) è applicato all’estremo B della leva.

La teoria di B. F. De BELIDOR (1698 -1761) De Belidor riprese la teoria di De la Hire, ma con ipotesi diverse sul punto di applicazione della forza ribaltante e del tipo di leva (che ne modifica la scomposizione). De la Hire De Belidor

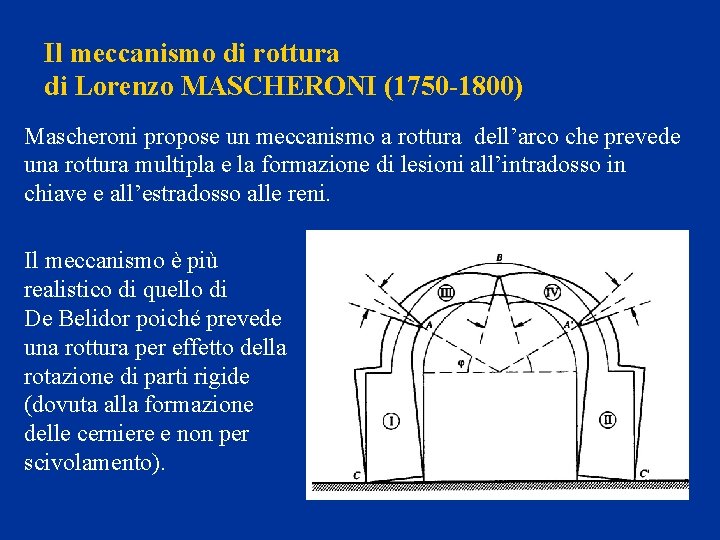
Il meccanismo di rottura di Lorenzo MASCHERONI (1750 -1800) Mascheroni propose un meccanismo a rottura dell’arco che prevede una rottura multipla e la formazione di lesioni all’intradosso in chiave e all’estradosso alle reni. Il meccanismo è più realistico di quello di De Belidor poiché prevede una rottura per effetto della rotazione di parti rigide (dovuta alla formazione delle cerniere e non per scivolamento).

COULOMB: IL PRINCIPIO DEI “MASSIMI E MINIMI” (1773) Oltre ad introdurre il problema della coesione delle malte e la presenza dell’attrito, Coulomb offrì un metodo di analisi per la determinazione dei meccanismi di rottura (quattro furono quelli da lui analizzati) e del relativo valore della SPINTA ORIZZONTALE IN CHIAVE variabile con l’angolo di rottura dei giunti alle reni. La teoria di Coulomb, in relazione ai modi di collasso per rotazione, è però inesatta: questo fu evidenziato da Persey nel 1825.

POST-COULOMBIANI (fine '700 -primi '800) Ebbero lo scopo di approfondire il discorso di Coulomb allargandone lo spettro di analisi fino alla definizione di otto meccanismi di collasso teorici, correggendone le incongruenze. L’obiettivo comune di tali studi è stato quello di considerare tutte le possibili combinazioni di rottura e definire la posizione della spinta orizzontale in chiave che nel primo lavoro di Coulomb manca totalmente. Non molto di nuovo però fu aggiunto da questi studi.

STUDI SULLE “CURVE DI PRESSIONE” Gli studi sulla ricerca della ‘curva delle pressioni’ negli archi, hanno coinvolto tutta la ricerca ottocentesca e costituiscono uno dei capitoli più significativi dell’indagine sulla stabilità delle volte. Un chiaro riconoscimento di questo aspetto è da attribuire a F. J. GERNSTNER il quale, nel 1831, introducendo per la prima volta nello studio degli archi gli strumenti grafici della linea delle pressioni e della linea di resistenza, ravvisò la possibilità di costruire un numero infinito di tali linee soddisfacenti l’equilibrio, con l’unica condizione che la linea passi all’interno dell’arco.

STUDI SULLE “CURVE DI PRESSIONE” Successivamente a questo approccio tutta la ricerca si concentrò sulla determinazione della vera posizione delle curve di pressione. Un primo studio sulle curve di pressione, ancora in linea con le conoscenze acquisite negli ultimi decenni, fu proposto da Moseley nel 1843 e successivamente divulgato da MERY a cui si deve, tra l’altro, il termine di "CURVA DELLE PRESSIONI" È il metodo più usato per la verifica di archi e volte, grazie alla sua semplicità e facilità di impiego. Costruisce il poligono funicolare del sistema di vettori che rappresentano i pesi di tutti i conci, con la condizione che questo poligono passi per punti prefissati.

La verifica degli archi mediante la curva delle pressioni PROCEDIMENTO DI MERY Le ipotesi alla base del metodo sono le seguenti: a. Arco simmetrico; b. Carichi simmetrici; c. Spinta trasmessa in chiave da un semiarco all’altro esclusivamente orizzontale; d. Spessore dell’arco uniforme; e. Massa concentrata lungo la linea d’asse. I pesi dei singoli conci vengono valutati e descritti come vettori in un’opportuna scala.

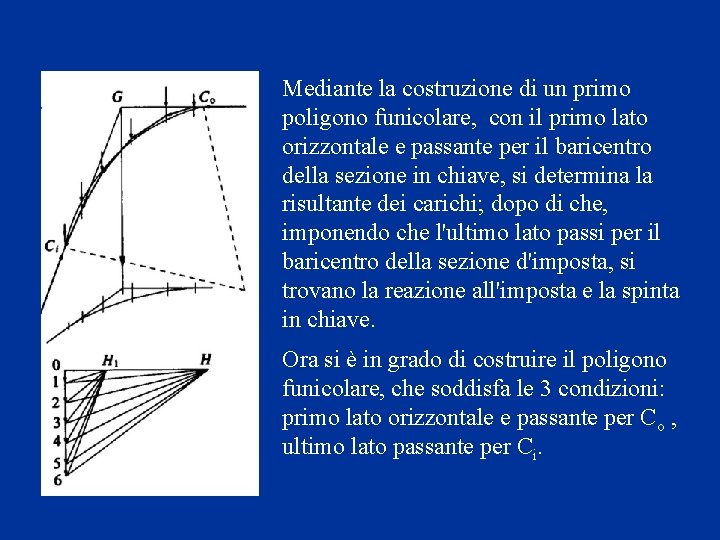
Mediante la costruzione di un primo poligono funicolare, con il primo lato orizzontale e passante per il baricentro della sezione in chiave, si determina la risultante dei carichi; dopo di che, imponendo che l'ultimo lato passi per il baricentro della sezione d'imposta, si trovano la reazione all'imposta e la spinta in chiave. Ora si è in grado di costruire il poligono funicolare, che soddisfa le 3 condizioni: primo lato orizzontale e passante per Co , ultimo lato passante per Ci.

Il poligono funicolare è quindi quello delle successive risultanti, nel senso che ciascun lato rappresenta la retta d’azione di tutte le forze che lo precedono, a partire dalla spinta in chiave, OH 1. La risultante rappresenta l’azione che una parte dell’arco esercita sulla successiva attraverso il giunto fra due conci, e può essere interpretata come l’azione interna che due conci si scambiano. Per questo motivo il poligono funicolare ottenuto è la curva delle pressioni.

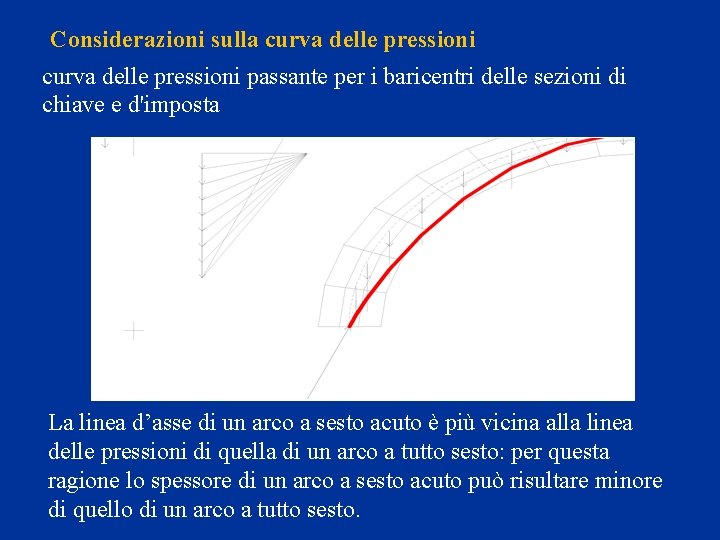
Considerazioni sulla curva delle pressioni passante per i baricentri delle sezioni di chiave e d'imposta La linea d’asse di un arco a sesto acuto è più vicina alla linea delle pressioni di quella di un arco a tutto sesto: per questa ragione lo spessore di un arco a sesto acuto può risultare minore di quello di un arco a tutto sesto.

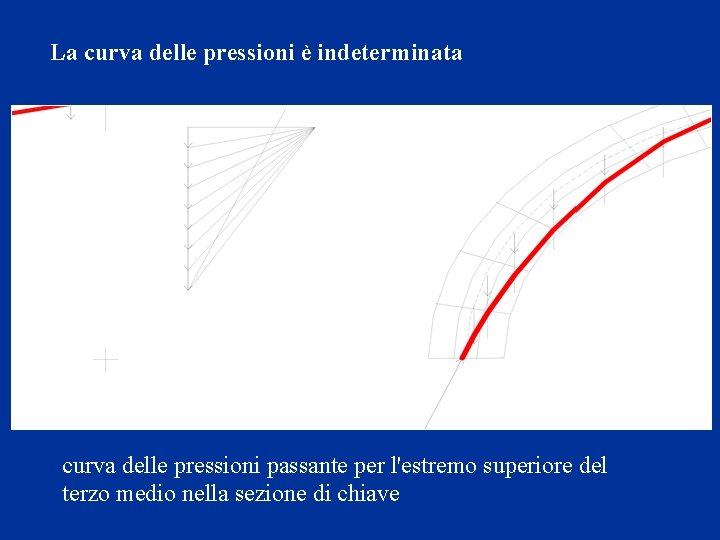
La curva delle pressioni è indeterminata curva delle pressioni passante per l'estremo superiore del terzo medio nella sezione di chiave

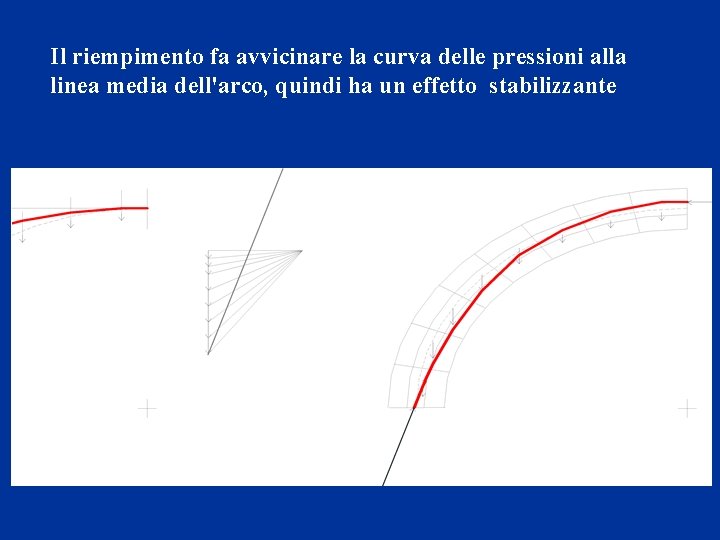
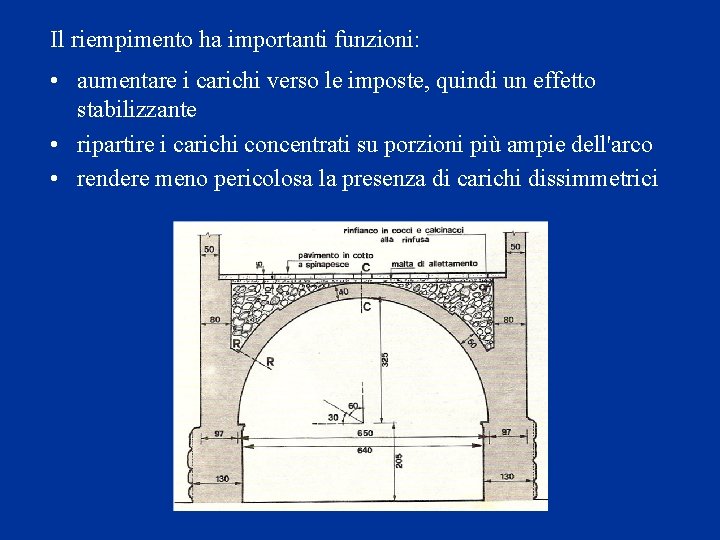
Il riempimento fa avvicinare la curva delle pressioni alla linea media dell'arco, quindi ha un effetto stabilizzante

Il riempimento ha importanti funzioni: • aumentare i carichi verso le imposte, quindi un effetto stabilizzante • ripartire i carichi concentrati su porzioni più ampie dell'arco • rendere meno pericolosa la presenza di carichi dissimmetrici

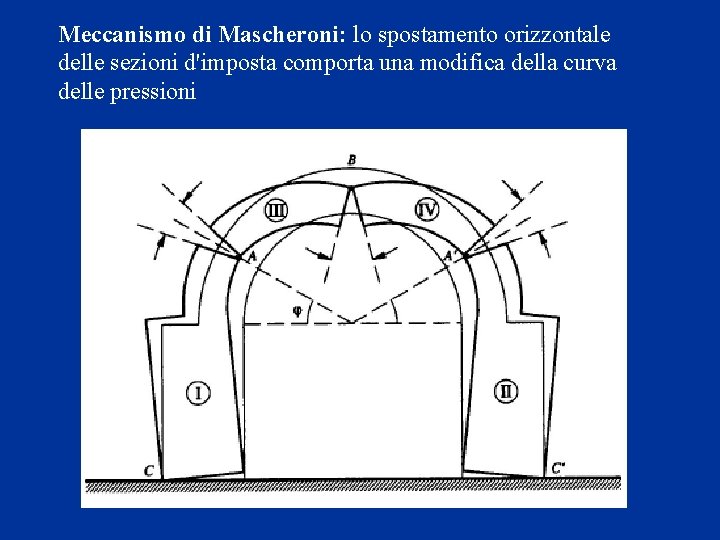
Meccanismo di Mascheroni: lo spostamento orizzontale delle sezioni d'imposta comporta una modifica della curva delle pressioni

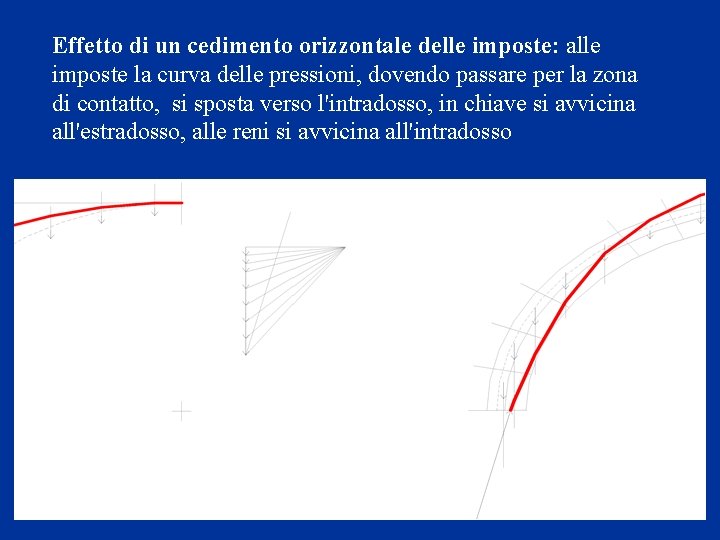
Effetto di un cedimento orizzontale delle imposte: alle imposte la curva delle pressioni, dovendo passare per la zona di contatto, si sposta verso l'intradosso, in chiave si avvicina all'estradosso, alle reni si avvicina all'intradosso

Se gli spostamenti orizzontali delle imposte sono piccoli, si formano delle fessure in chiave e alle reni. Quando gli spostamenti sono più grandi, l'ampiezza delle fessure aumenta e lo schema statico del sistema cambia. Affinché si abbia il crollo dell'arco, le imposte devono spostarsi notevolmente, perché le porzioni III e IV, mano che si abbassano, occupano sempre maggiore spazio. Il crollo è preannunciato da evidenti cambiamenti di forma dell'arco.

n La linea delle pressioni descrive le azioni reciproche due conci adiacenti si scambiano. Se si fa riferimento alla n-esima sezione trasversale (Sn), il lato Sn+1 del poligono funicolare è la risultante Fn delle (n+1) forze che precedono la sezione considerata. n Questa risultante non passa, in generale, per il baricentro della sezione considerata, che è individuato dalla linea d’asse. Dà pertanto origine a una sollecitazione composta da: Azione assiale, Nn; Azione tagliante, Tn ; Momento flettente, Mn.

La forma della curva delle pressioni fornisce alcune informazioni che hanno diretta attinenza con la stabilità dell’arco, cioè: 1. L’ultimo lato del poligono funicolare rappresenta l’azione trasmessa dall’arco alla struttura di sostegno: è tanto più vicina alla verticale quanto più la risultante dei carichi agenti sul semiarco è prossima all’imposta; 2. La forma della linea delle pressioni deve essere messa in relazione con la forma della linea d’asse dell’arco.

La linea delle pressioni può essere vista come un indice della stabilità di un arco: tanto maggiore è l’eccentricità, tanto maggiore deve essere lo spessore dell’arco affinché la linea rimanga per lo meno all’interno della sezione, anche se sarebbe preferibile che si mantenesse all’interno del terzo medio per evitare la parzializzazione della sezione e il corrispondente aggravio tensionale. La linea d’asse di un arco a sesto acuto è più vicina alla linea delle pressioni di quella di un arco a tutto sesto: per questa ragione lo spessore di un arco a sesto acuto può risultare minore di quello di un arco a tutto sesto.

METODO DI MERY L'analisi di Mery considera come situazione limite per l'arco quella corrispondente alla formazione delle prime fessure. Lo studio e la pratica mostrano che le prime fessure, in archi simmetrici e simmetricamente caricati, si verificano in corrispondenza della sezione di chiave e delle due sezioni (reni) simmetriche rispetto all’asse verticale di simmetria ed inclinate rispetto a tale asse di 60 °

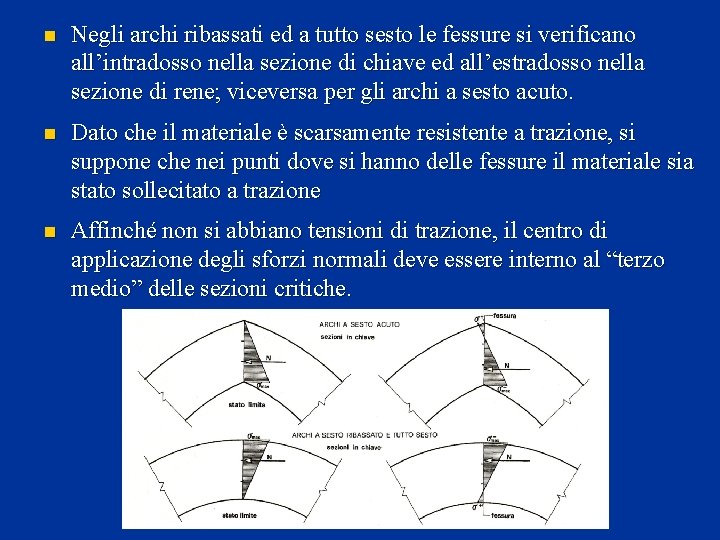
n Negli archi ribassati ed a tutto sesto le fessure si verificano all’intradosso nella sezione di chiave ed all’estradosso nella sezione di rene; viceversa per gli archi a sesto acuto. n Dato che il materiale è scarsamente resistente a trazione, si suppone che nei punti dove si hanno delle fessure il materiale sia stato sollecitato a trazione n Affinché non si abbiano tensioni di trazione, il centro di applicazione degli sforzi normali deve essere interno al “terzo medio” delle sezioni critiche.

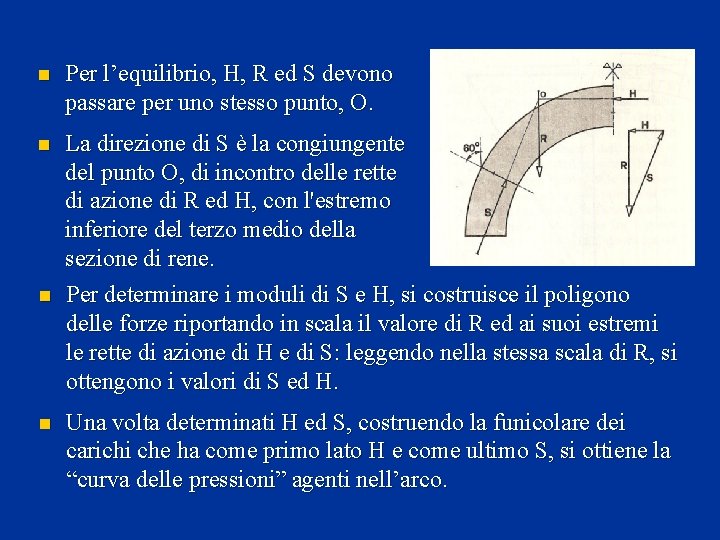
Prendiamo in esame un semiarco a tutto sesto, simmetrico e simmetricamente caricato. La risultante dei carichi in corrispondenza della sezione di chiave, per la simmetria, è una forza H orizzontale. Nella condizione limite, H è applicata all'estremo superiore del “terzo medio”. La reazione S della sezione di rene, nella condizione limite, è applicata all’estremo inferiore del “terzo medio”. Le azioni H ed S dovranno formare un sistema di forze equilibrato con la risultante dei carichi applicati, R.

n Per l’equilibrio, H, R ed S devono passare per uno stesso punto, O. n La direzione di S è la congiungente del punto O, di incontro delle rette di azione di R ed H, con l'estremo inferiore del terzo medio della sezione di rene. Per determinare i moduli di S e H, si costruisce il poligono delle forze riportando in scala il valore di R ed ai suoi estremi le rette di azione di H e di S: leggendo nella stessa scala di R, si ottengono i valori di S ed H. n n Una volta determinati H ed S, costruendo la funicolare dei carichi che ha come primo lato H e come ultimo S, si ottiene la “curva delle pressioni” agenti nell’arco.

n Una volta determinata la curva delle pressioni, si è in grado di effettuare le verifiche di resistenza delle sezioni dell'arco e di stabilità delle spalle.

La verifica degli archi fra elasticità e plasticità Nel 1867 Winkler sostenne che la vera curva delle pressioni, sulla base della teoria dell’elasticità, è quella che meno si scosta dalla linea d’asse dell’arco. La applicazione della teoria dell’elasticità alle strutture murarie non è però giustificata in un ambito di calcolo a rottura per il quale si prescinde dalla deformabilità, e si considerano rigidi i conci.

La teoria di Heyman – The safe theorem Il problema è stato ricondotto, da Jacques Heyman in The masonry arch (1982), a una formulazione coerente con i metodi del calcolo a rottura. Ipotesi di base: a. Non può avvenire rottura a scorrimento: due conci non possono scorrere relativamente nel piano di contatto; b. La muratura non ha resistenza a trazione; c. La muratura ha resistenza a compressione illimitata.

La teoria di Heyman – The safe theorem Il teorema di Heyman, che fornisce una delimitazione inferiore del carico di collasso di un arco afferma che: “Se esiste una linea di pressioni per l’arco completo, che sia in equilibrio con i carichi applicati, incluso il peso proprio, e che risulti ovunque e in ogni sezione interna allo spessore dell’arco, allora l’arco può considerarsi in condizioni di sicurezza. ”

Secondo Heyman, quindi, non ha interesse determinare l’effettiva curva delle pressioni, mentre è sufficiente mostrare che esiste almeno un sistema di forze interne equilibrato e che soddisfi le condizioni imposte dal teorema. La differente posizione della curva di pressione sulla sezione può produrre la formazione di fessure localizzate, corrispondenti, in termini cinematici, alla formazione di cerniere interne che possono coalizzarsi a formare un meccanismo.

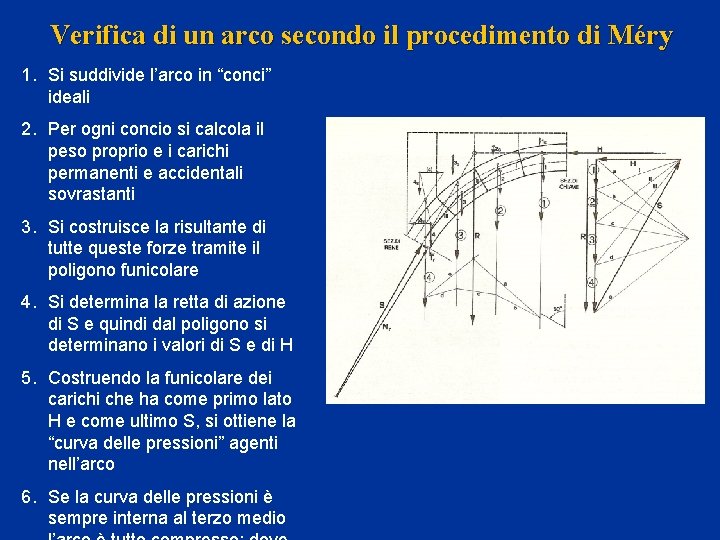
Verifica di un arco secondo il procedimento di Méry 1. Si suddivide l’arco in “conci” ideali 2. Per ogni concio si calcola il peso proprio e i carichi permanenti e accidentali sovrastanti 3. Si costruisce la risultante di tutte queste forze tramite il poligono funicolare 4. Si determina la retta di azione di S e quindi dal poligono si determinano i valori di S e di H 5. Costruendo la funicolare dei carichi che ha come primo lato H e come ultimo S, si ottiene la “curva delle pressioni” agenti nell’arco 6. Se la curva delle pressioni è sempre interna al terzo medio

Verifiche di resistenza n Per ogni concio conosciamo il valore di M (N·e) e del taglio agenti nelle sezioni di estremità n Il valore di T dovrà essere inferiore alla forza di attrito (f · N); considerando un opportuno coefficiente di sicurezza, dovrà risultare: T ≤(f · N)/1, 5 n Dovrà inoltre essere verificato che le tensioni tangenziali non siano superiori a quelle ammissibili e dunque: per centro di pressione interno al terzo medio: τ max =3·T/(2·b·s) ≤ τ amm

per centro di pressione esterno al terzo medio: τ max =T/(b·u) ≤ τ amm n Infine si dovrà effettuare la verifica delle tensioni normali: per centro di pressione interno al terzo medio: σ = [ N/(b·s) ] · (1 ± 6·e/s) ≤ σ amm per centro di pressione esterno al terzo medio: σ = [ 2·N/(3·b·u) ] ≤ σ amm

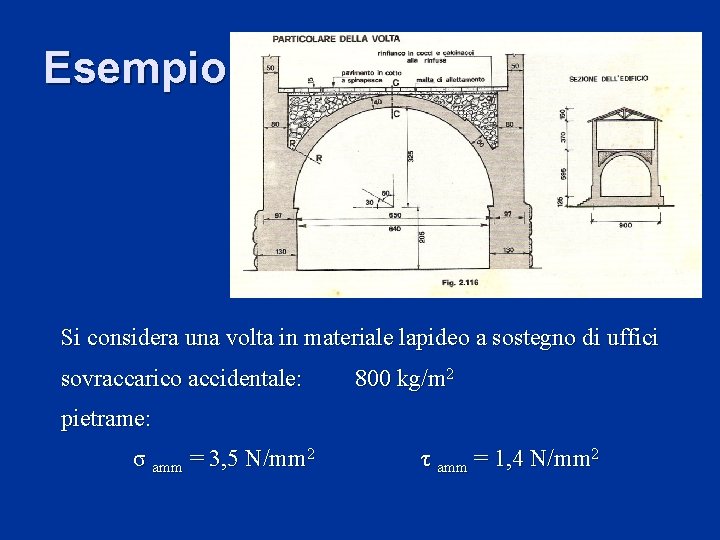
Esempio Si considera una volta in materiale lapideo a sostegno di uffici sovraccarico accidentale: 800 kg/m 2 pietrame: σ amm = 3, 5 N/mm 2 τ amm = 1, 4 N/mm 2

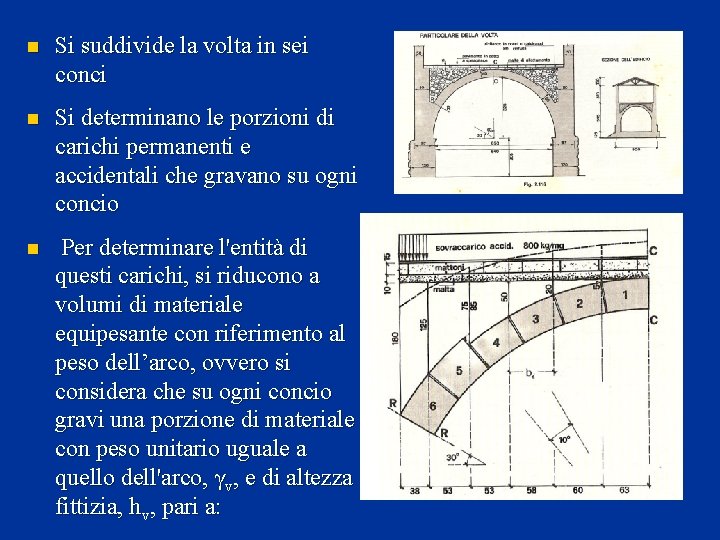
n Si suddivide la volta in sei conci n Si determinano le porzioni di carichi permanenti e accidentali che gravano su ogni concio n Per determinare l'entità di questi carichi, si riducono a volumi di materiale equipesante con riferimento al peso dell’arco, ovvero si considera che su ogni concio gravi una porzione di materiale con peso unitario uguale a quello dell'arco, γv, e di altezza fittizia, hv, pari a:

I materiali presenti sono: Pavimento di mattoni γp=1800 kg/m 3 Sottofondo di allettamento γs=2300 kg/m 3 Rinfianco in coccio o calcinaccio γr=1300 kg/m 3 Arco di pietrame γv = 2600 kg/m 3 Coefficienti di omogeneizzazione: γp/ γv =0, 69 kg/m 3 γs/ γv =0, 88 kg/m 3 γr/ γv =0, 50 kg/m 3

Moltiplicando le altezze effettive dei materiali per i coefficienti di omogeneizzazione, si ottengono le altezze fittizie riferite al peso dell'arco in pietrame. Per il sovraccarico avremo un'altezza fittizia pari a: hsv=800/2600=0, 31 m

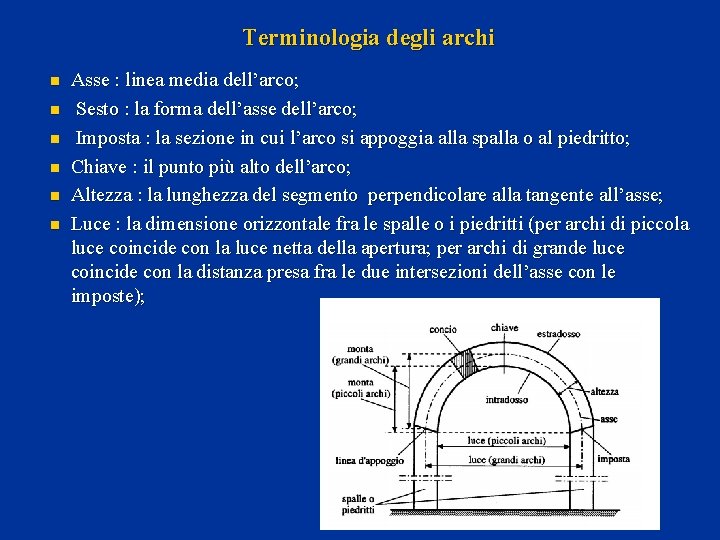
I pesi dei conci si valutano tramite Pi = [(hi-1+hi)·bi·γv]/2

Si applica il procedimento di Méry n Si costruisce la risultante di tutte le forze tramite il poligono funicolare n La reazione H, passante per il terzo medio superiore della sezione di chiave, per la simmetria di struttura e di carico ha direzione orizzontale, h-h n La reazione S agisce in direzione s-s, congiungente il punto di intersezione delle rette r-r e h-h con il terzo medio inferiore nella sezione di rene n Sullo stesso sostegno del poligono delle forze, si riportano le direzioni s-s e h-h, il cui punto di intersezione, Ps, individua, nella scala delle forze, l’entità delle reazioni al rene e in chiave n Infine si traccia la curva delle pressioni

Verifiche Sezione di chiave N=6800 kg (azione nel terzo medio superiore) σmax=2·N/(b·s)= 3, 4 kg/cm 2 < 35 kg/cm 2 Sezione di rene N=12635 kg (azione giacente al terzo medio inferiore) T=600 kg σmax=2·N/(b·s)= 5 kg/cm 2 < 35 kg/cm 2 τmax=3·T/(2·b·s)= 0, 2 kg/cm 2 < 14 kg/cm 2 Sezione con minor spessore più sollecitata (4) (s=40 cm) N=9330 kg T=550 kg σmax = [ N/(b·s) ] · (1 + 6·e/s) = 4 < 35 kg/cm 2 τmax=3·T/(2·b·s)= 0, 21 kg/cm 2 < 14 kg/cm 2

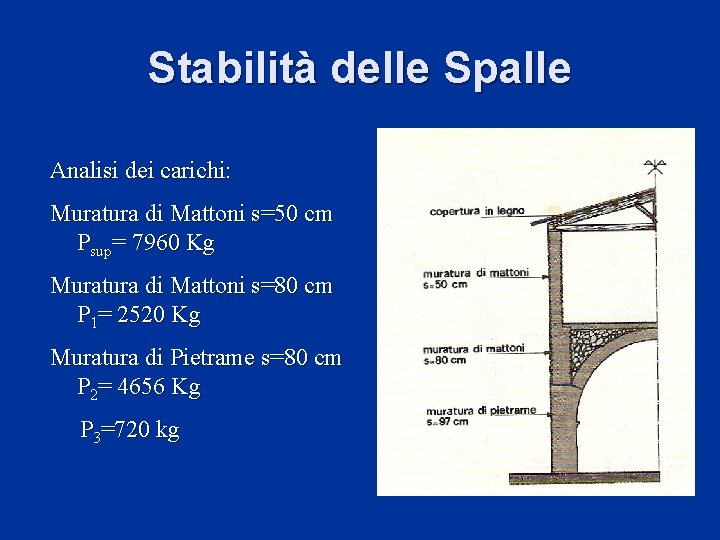
Stabilità delle Spalle Analisi dei carichi: Muratura di Mattoni s=50 cm Psup= 7960 Kg Muratura di Mattoni s=80 cm P 1= 2520 Kg Muratura di Pietrame s=80 cm P 2= 4656 Kg P 3=720 kg

Componendo graficamente i carichi verticali con l’azione S prodotta dalla volta otteniamo Sezione K – K Rk=27380 kg Nk=26500 kg Tk = 6800 kg e = 25 cm > 97/6=16, 17 cm (azione esterna al terzo medio) u = (97/2) – 25=23, 5 cm σmax=2·N/(3·b·u)= 7, 52 kg/cm 2 < 35 kg/cm 2 τmax=·T/(b·u)= 1, 45 kg/cm 2 < 14 kg/cm 2

Sezione J – J con l’azione aggiuntiva P 4=6395 kg Rj=33500 kg Nj=32895 kg Tj = 6800 kg e = 50 cm > 130/6=22 cm (azioni esterna al terzo medio) u = (130/2) – 50=15 cm σmax=2·N/(3·b·u)= 14, 62 kg/cm 2 < 35 kg/cm 2 τmax=·T/(b·u)= 2, 27 kg/cm 2 < 14 kg/cm 2 L’arco risulta verificato in tutte le sezioni critiche

Riferimenti bibliografici Renato S. Olivito, Statica e stabilità delle costruzioni murarie, Pitagora Ed. Bologna, 2003 Jacques Heyman, The masonry arch, 1982 Mario Como, Statica delle costruzioni storiche in muratura