Chapter 3 Chang ChiChung 2007 4 12 The

Chapter 3 Chang Chi-Chung 2007. 4. 12

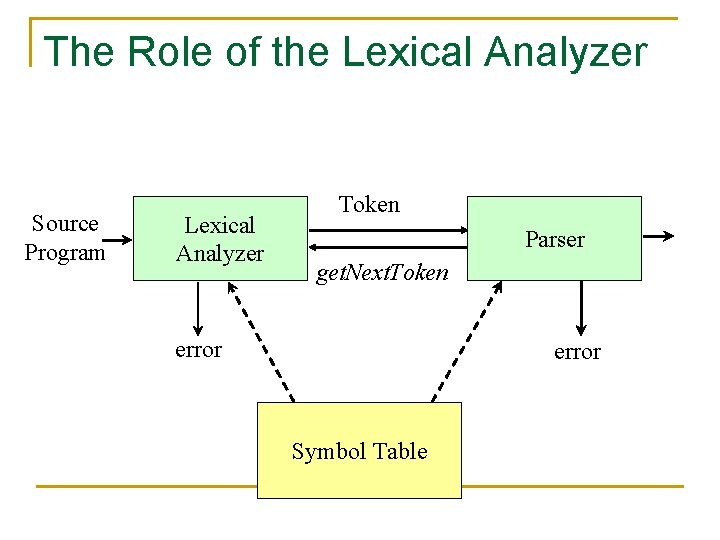
The Role of the Lexical Analyzer Source Program Lexical Analyzer Token Parser get. Next. Token error Symbol Table

The Reason for Using the Lexical Analyzer n Simplifies the design of the compiler q n Compiler efficiency is improved q q n LL(1) or LR(1) parsing with 1 token lookahead would not be possible (multiple characters/tokens to match) Systematic techniques to implement lexical analyzers by hand or automatically from specifications Stream buffering methods to scan input Compiler portability is enhanced q Input-device-specific peculiarities can be restricted to the lexical analyzer.

Tokens, Patterns, and Lexemes n Token (符號單元) q q n Pattern (樣本) q q n A pair consisting of a token name and optional arrtibute value. Example: num, id A description of the form for the lexemes of a token. Example: “non-empty sequence of digits”, “letter followed by letters and digits” Lexeme (詞) q q A sequence of characters that matches the pattern for a token. Example: 123, abc

Example: Tokens, Patterns, and Lexemes Token Pattern Lexeme if characters i f if else characters e l s e else comparison < or > or <= or >= or == or != <=, != id pi, score, D 2 number letter followed by letters and digits any numeric constant literal anything but “, surrounded by “’s “core dump” 3. 14, 0, 6. 23

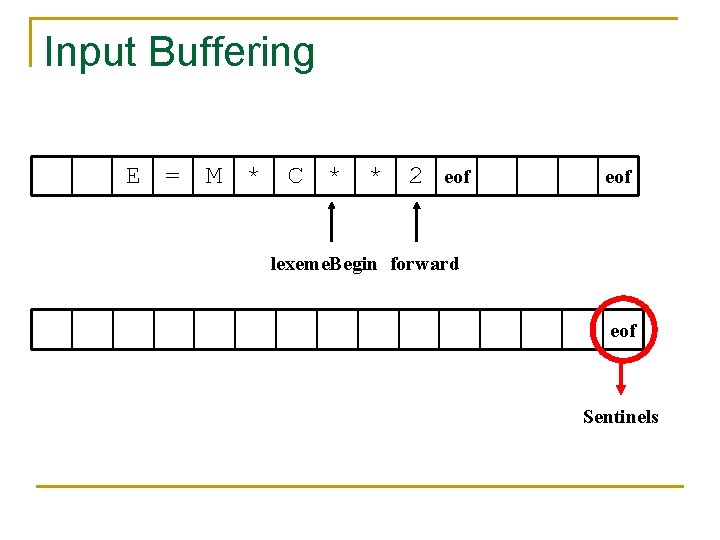
Input Buffering E = M * C * * 2 eof lexeme. Begin forward eof Sentinels

Strings and Languages n Alphabet q n An alphabet is a finite set of symbols (characters) String q A string is a finite sequence of symbols from n n n s denotes the length of string s denotes the empty string, thus = 0 Language q A language is a countable set of strings over some fixed alphabet n n Abstract Language Φ {ε}

String Operations n Concatenation (連接) q n n The concatenation of two strings x and y is denoted by xy Identity (單位元素) q The empty string is the identity under concatenation. q s=s =s Exponentiation q q Define s 0 = si = si-1 s for i > 0 By Define s 1 = s s 2 = ss

Language Operations n n n Union L M = { s s L or s M } Concatenation L M = { xy x L and y M} Exponentiation L 0 = { } Li = Li-1 L Kleene closure (封閉包) L* = ∪i=0, …, Li Positive closure L+ = ∪i=1, …, Li

Regular Expressions n Regular Expressions q q q n A convenient means of specifying certain simple sets of strings. We use regular expressions to define structures of tokens. Tokens are built from symbols of a finite vocabulary. Regular Sets q The sets of strings defined by regular expressions.

Regular Expressions n Basis symbols: q q n If r and s are regular expressions denoting languages L(r) and M(s) respectively, then q q n is a regular expression denoting language L( ) = { } a is a regular expression denoting L(a) = {a} r s is a regular expression denoting L(r) M(s) rs is a regular expression denoting L(r)M(s) r* is a regular expression denoting L(r)* (r) is a regular expression denoting L(r) A language defined by a regular expression is called a regular set.

Operator Precedence Associative * highest left concatenation Second left | lowest left

Algebraic Laws for Regular Expressions Law Description r|s=s|r r|(s|t)=(r|s)|t r(st) = (rs)t r(s|t) = rs | rt (s|t)r = sr | tr | is commutative | is associative concatenation distributes over | εr = rε = r ε is the identity for concatenation r* = ( r |ε)* ε is guaranteed in a closure r** = r* * is idempotent

Regular Definitions n If Σ is an alphabet of basic symbols, then a regular definitions is a sequence of definitions of the form: d 1 r 1 d 2 r 2 … dn rn q q n Each di is a new symbol, not in Σ and not the same as any other of d’s. Each ri is a regular expression over the alphabet {d 1, d 2, …, di-1 } Any dj in ri can be textually substituted in ri to obtain an equivalent set of definitions

Example: Regular Definitions letter_ A | B | … | Z | a | b | … | z | _ digit 0 | 1 | … | 9 id letter_ ( letter_ | digit )* Regular definitions are not recursive digits digit wrong

Extensions of Regular Definitions n One or more instance q q n Zero or one instance q n r? = r |ε Character classes q q n r+ = rr* = r*r r* = r+ | ε [a-z] = a b c … z [A-Za-z] = A|B|…|Z|a|…|z Example q q digit [0 -9] num digit+ (. digit+)? ( E (+ -)? digit+ )?

Regular Definitions and Context-Free Grammars stmt if expr then stmt else stmt ws ( blank | tab | newline )+ expr term relop term Regular Definitions term id digit [0 -9] num letter [A-Za-z] if then else relop < <= <> > >= = id letter ( letter | digit )* num digit+ (. digit+)? ( E (+ | -)? digit+ )?

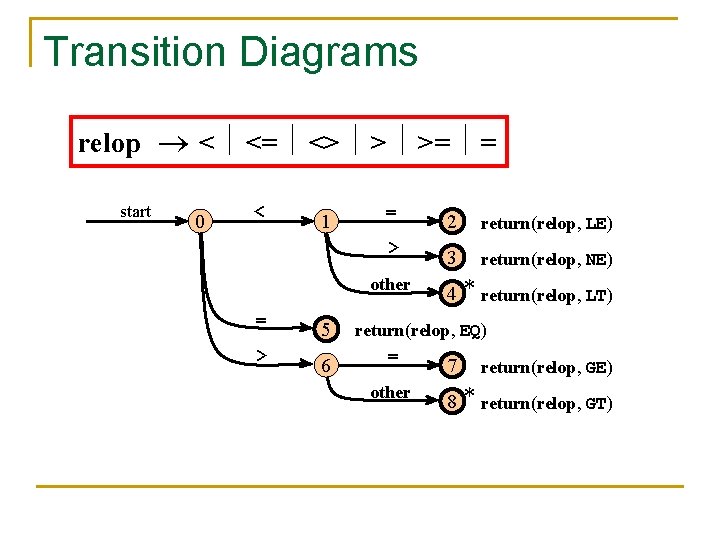
Transition Diagrams relop < <= <> > >= = start 0 < 1 = 2 return(relop, LE) > 3 return(relop, NE) other = 5 > 6 4 * return(relop, LT) return(relop, EQ) = 7 return(relop, GE) other 8 * return(relop, GT)

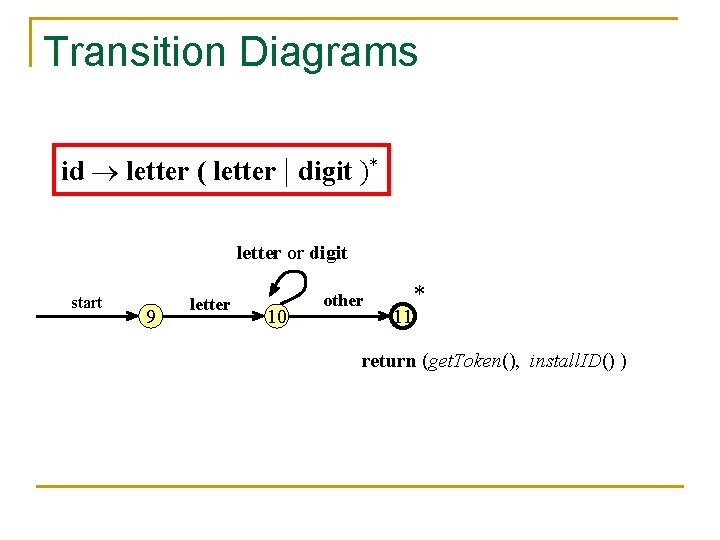
Transition Diagrams id letter ( letter | digit )* letter or digit start 9 letter 10 other * 11 return (get. Token(), install. ID() )

Finite Automata n Finite Automata are recognizers. q q q n Two kind of the Finite Automata q q n FA simply say “Yes” or “No” about each possible input string. A FA can be used to recognize the tokens specified by a regular expression Use FA to design of a Lexical Analyzer Generator Nondeterministic finite automata (NFA) Deterministic finite automata (DFA) Both DFA and NFA are capable of recognizing the same languages.

NFA Definitions n NFA = { S, , , s 0, F } q q A finite set of states S A set of input symbols Σ n q input alphabet, ε is not in Σ A transition function n : S S q A special start state s 0 q A set of final states F, F S (accepting states)

Transition Graph for FA is a state is a transition is a the start state is a final state

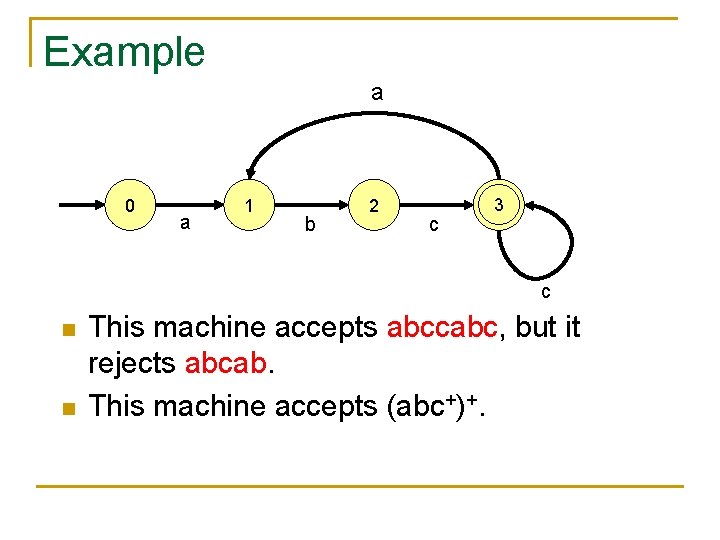
Example a 0 a 1 b 2 c 3 c n n This machine accepts abccabc, but it rejects abcab. This machine accepts (abc+)+.

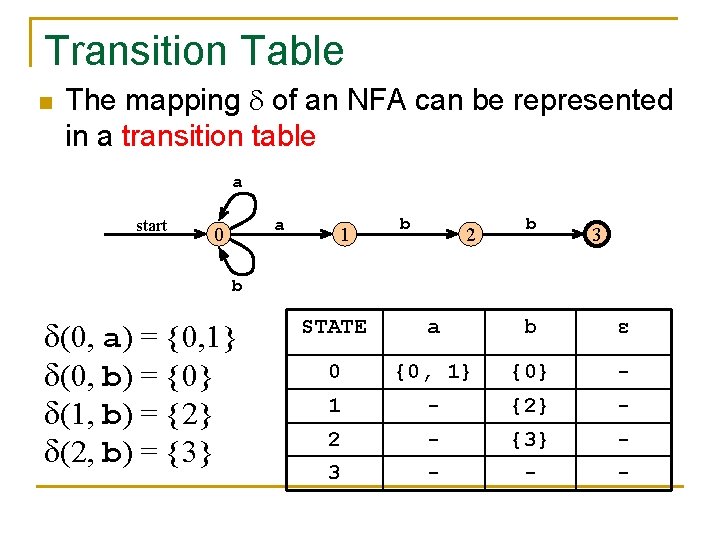
Transition Table n The mapping of an NFA can be represented in a transition table a start a 0 1 b 2 b 3 b (0, a) = {0, 1} (0, b) = {0} (1, b) = {2} (2, b) = {3} STATE a b ε 0 {0, 1} {0} - 1 - {2} - 2 - {3} - 3 - - -

DFA n DFA is a special case of an NFA q q n There are no moves on input ε For each state s and input symbol a, there is exactly one edge out of s labeled a. Both DFA and NFA are capable of recognizing the same languages.

Simulating a DFA n Input q n An input string x terminated by an end-of-file character eof. A DFA D with start state s 0, accepting states F, and transition function move. Output q Answer “yes” if D accepts x; “no” otherwise. s = s 0 c = next. Char(); while ( c != eof ) { s = move(s, c); c = next. Char(); } if (s is in F ) return “yes”; else return “no”;

S = {0, 1, 2, 3} = {a, b} s 0 = 0 F = {3} NFA vs DFA a start a 0 b b 1 b 2 3 (a | b)*abb b 0 a 1 a b 2 b 3 a a

The Regular Language n The regular language defined by an NFA is the set of input strings it accepts. q n Example: (a b)*abb for the example NFA An NFA accepts an input string x if and only if q q there is some path with edges labeled with symbols from x in sequence from the start state to some accepting state in the transition graph A state transition from one state to another on the path is called a move.

Theorem n The followings are equivalent q q q Regular Expression NFA DFA Regular Language Regular Grammar

Convert Concept Regular Expression Minimization Deterministic Finite Automata Nondeterministic Finite Automata Deterministic Finite Automata

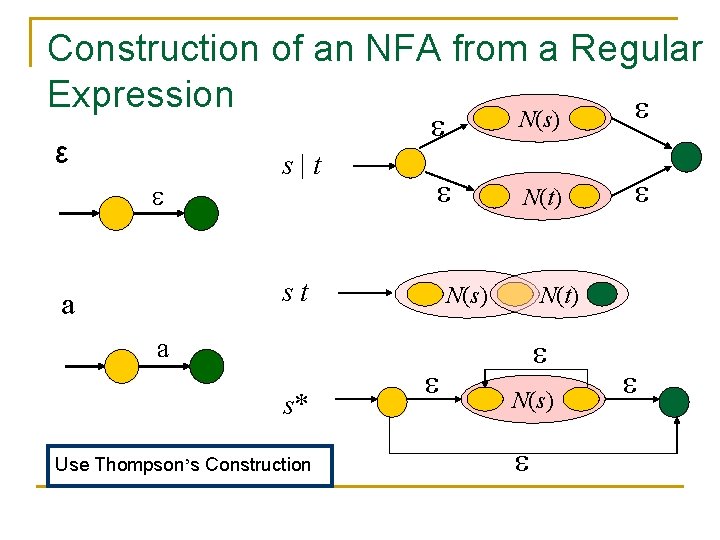
Construction of an NFA from a Regular Expression ε s|t N(s) N(t) st a a s* Use Thompson’s Construction N(s) N(t) N(s)

r 11 Example n r 9 ( a | b )* a b b r 7 r 5 ( r 3 ) r 1 | r 2 a b r 8 r 6 * r 4 r 10 b b a r 3 = r 4

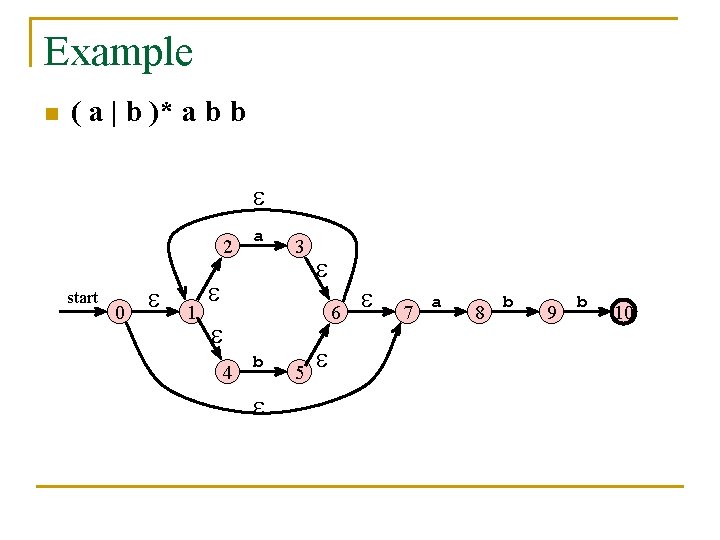
Example n ( a | b )* a b b 2 start 0 1 a 3 4 6 b 5 7 a 8 b 9 b 10

Conversion of an NFA to a DFA n The subset construction algorithm converts an NFA into a DFA using the following operation. Operation Description ε- closure(s) Set of NFA states reachable from NFA state s on εtransitions alone. ε- closure(T) Set of NFA states reachable from some NFA state s in set T on ε-transitions alone. = ∪s in T ε- closure(s) move(T, a) Set of NFA states to which there is a transition on input symbol a from some state s in T

Subset Construction(1) Initially, -closure(s 0) is the only state in Dstates and it is unmarked; while (there is an unmarked state T in Dstates) { mark T; for (each input symbol a ) { U = -closure( move(T, a) ); if (U is not in Dstates) add U as an unmarked state to Dstates Dtran[T, a] = U } }

Computing ε- closure(T)

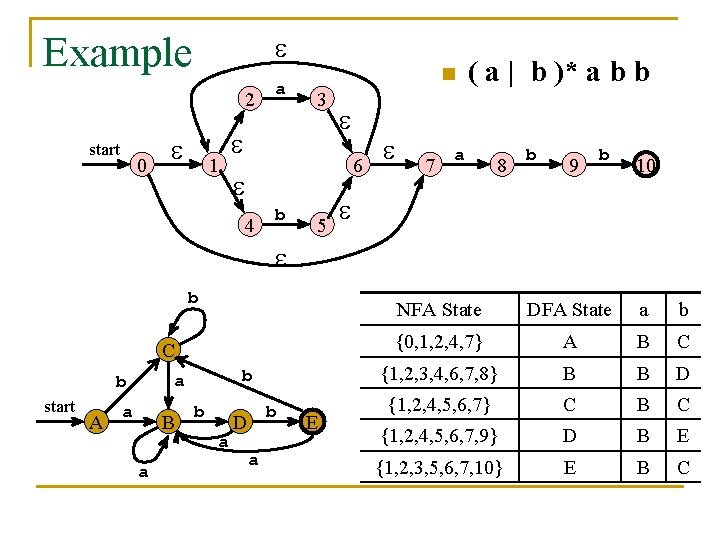
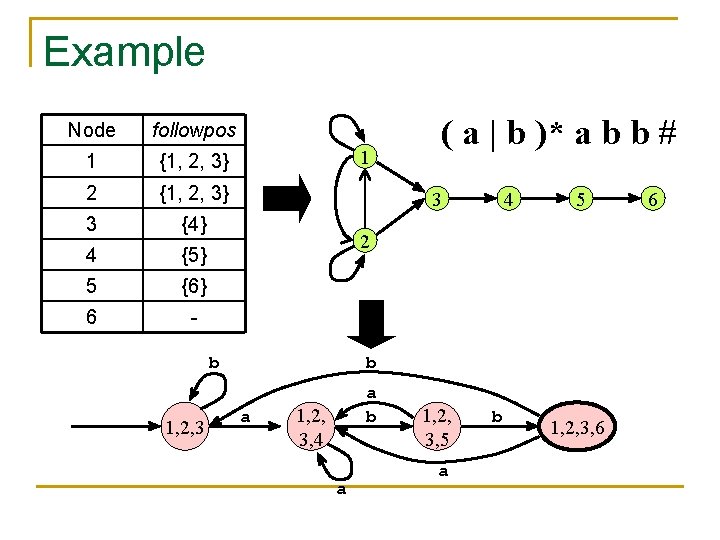
Example 2 start 0 1 a n 3 6 4 b 5 7 ( a | b )* a b b a 8 b 9 b 10 b C start A b a B a b a D a b E NFA State DFA State a b {0, 1, 2, 4, 7} A B C {1, 2, 3, 4, 6, 7, 8} B B D {1, 2, 4, 5, 6, 7} C B C {1, 2, 4, 5, 6, 7, 9} D B E {1, 2, 3, 5, 6, 7, 10} E B C

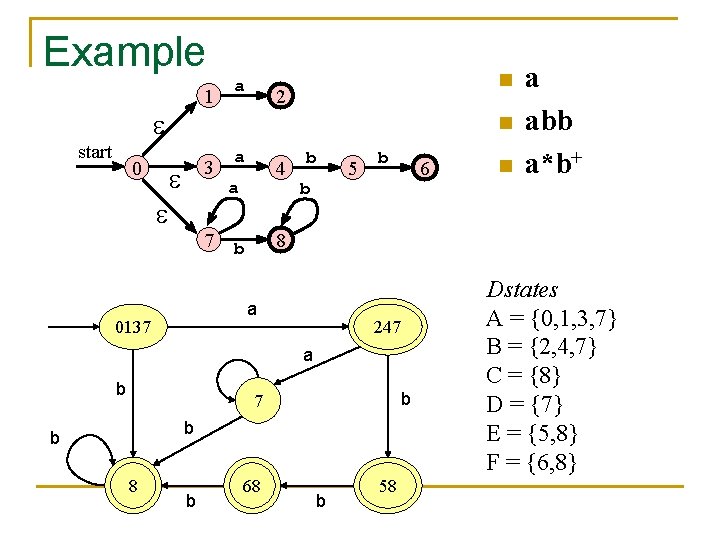
Example 1 start 0 a n 2 n 3 7 a 4 a b b b 6 247 a b b 7 b b 8 b n 8 b a 0137 5 a abb a*b+ 68 b 58 Dstates A = {0, 1, 3, 7} B = {2, 4, 7} C = {8} D = {7} E = {5, 8} F = {6, 8}

Minimizing the DFA n Step 1 q n Step 2 q n Split Procedure Step 3 q n Start with an initial partition II with two group: F and S-F (aceepting and nonaccepting) If ( IInew = II ) IIfinal = II and continue step 4 else II = IInew and go to step 2 Step 4 q q Construct the minimum-state DFA by IIfinal group. Delete the dead state

Split Procedure Initially, let IInew = II for ( each group G of II ) { Partition G into subgroup such that two states s and t are in the same subgroup if and only if for all input symbol a, states s and t have transition on a to states in the same group of II. /* at worst, a state will be in a subgroup by itself */ replace G in IInew by the set of all subgroup formed }

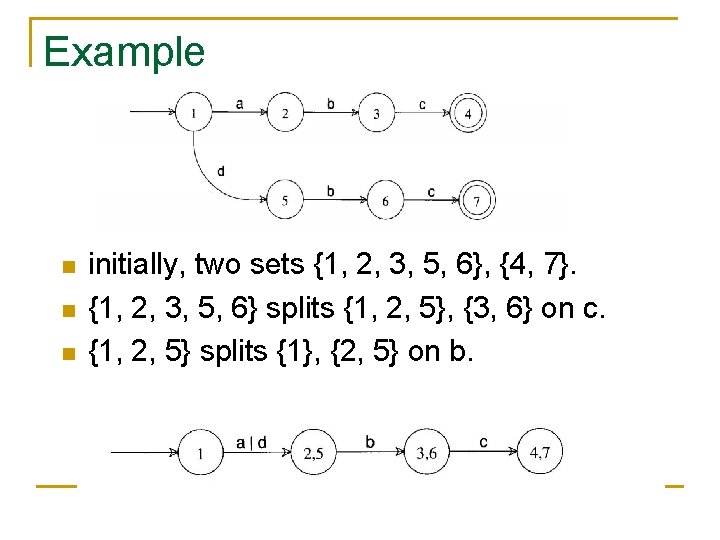
Example n n n initially, two sets {1, 2, 3, 5, 6}, {4, 7}. {1, 2, 3, 5, 6} splits {1, 2, 5}, {3, 6} on c. {1, 2, 5} splits {1}, {2, 5} on b.

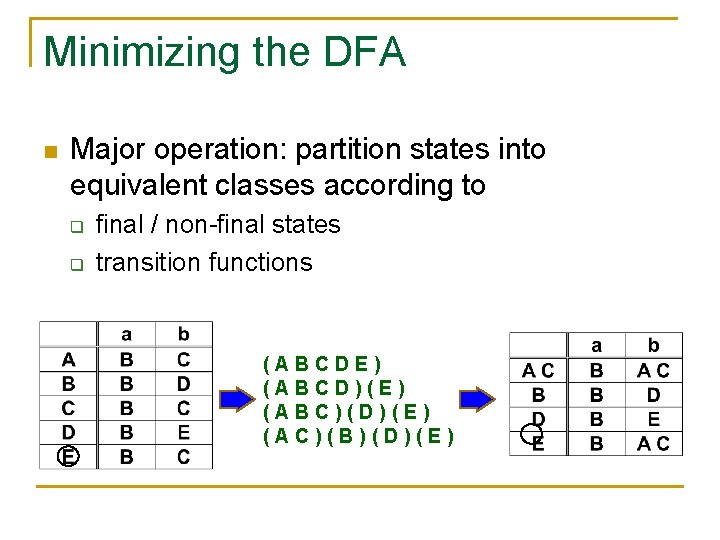
Minimizing the DFA n Major operation: partition states into equivalent classes according to q q final / non-final states transition functions (ABCDE) (ABCD)(E) (ABC)(D)(E) (AC)(B)(D)(E)

Important States of an NFA n The “important states” of an NFA are those without an -transition, that is q n n if move({s}, a) for some a then s is an important state The subset construction algorithm uses only the important states when it determines -closure ( move(T, a) ) Augment the regular expression r with a special end symbol # to make accepting states important: the new expression is r#

Converting a RE Directly to a DFA n n n Construct a syntax tree for (r)# Traverse the tree to construct functions nullable, firstpos, lastpos, and followpos Construct DFA D by algorithm 3. 62

Function Computed From the Syntax Tree n nullable(n) q n firstpos(n) q n The set of positions that can match the first symbol of a string generated by the subtree at node n lastpos(n) q n The subtree at node n generates languages including the empty string The set of positions that can match the last symbol of a string generated be the subtree at node n followpos(i) q The set of positions that can follow position i in the tree

Rules for Computing the Function Node n nullable(n) firstpos(n) lastpos(n) A leaf labeled by true A leaf with position i false {i} n = c 1 | c 2 nullable(c 1) or nullable(c 2) firstpos(c 1) firstpos(c 2) lastpos(c 1) lastpos(c 2) n = c 1 c 2 nullable(c 1) and nullable(c 2) if ( nullable(c 1) ) firstpos(c 1) firstpos(c 2) else firstpos(c 1) if ( nullable(c 2) ) lastpos(c 1) lastpos(c 2) else lastpos(c 2) n = c 1* true firstpos(c 1) lastpos(c 1)

Computing followpos for (each node n in the tree) { //n is a cat-node with left child c 1 and right child c 2 if ( n == c 1．c 2) for (each i in lastpos(c 1) ) followpos(i) = followpos(i) firstpos(c 2); else if (n is a star-node) for ( each i in lastpos(n) ) followpos(i) = followpos(i) firstpos(n); }

Converting a RE Directly to a DFA Initialize Dstates to contain only the unmarked state firstpos(n 0), where n 0 is the root of syntax tree T for (r)#; while ( there is an unmarked state S in Dstates ) { mark S; for ( each input symbol a ) { let U be the union of followpos(p) for all p in S that correspond to a; if (U is not in Dstates ) add U as an unmarked state to Dstates Dtran[S, a] = U; } }

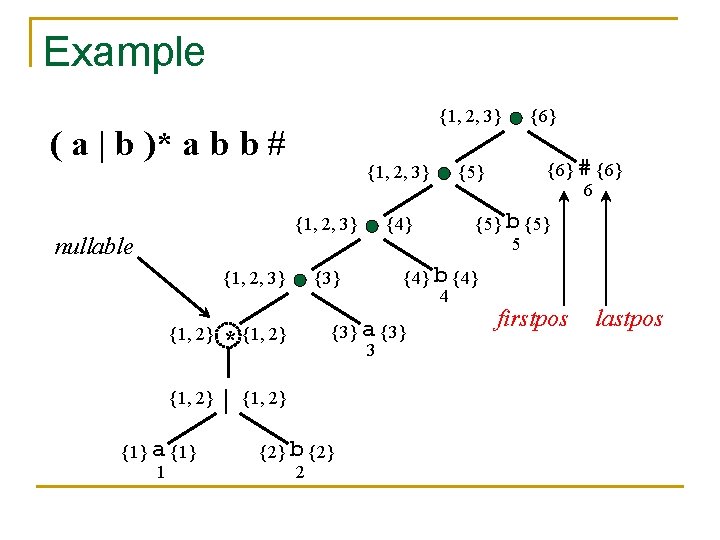
○ Example # ○ ( a | b )* a b b # ○ n ○ a 3 * | a 1 b 2 b 4 b 5 6 n = ( a | b )* a nullable(n) = false firstpos(n) = { 1, 2, 3 } lastpos(n) = { 3 } followpos(1) = {1, 2, 3 }

Example {1, 2, 3} ( a | b )* a b b # {1, 2, 3} nullable {1, 2, 3} {1, 2} * {1, 2} | {1, 2} {1} a {1} 1 {3} {4} {6} # {6} 6 {5} b {5} 5 {4} b {4} 4 {3} a {3} 3 {2} b {2} 2 {5} {6} firstpos lastpos

Example Node followpos 1 {1, 2, 3} 2 {1, 2, 3} 3 {4} 4 {5} 5 {6} 6 - 1 3 4 5 2 b 1, 2, 3 ( a | b )* a b b # b a a b 1, 2, 3, 4 a 1, 2, 3, 5 a b 1, 2, 3, 6 6

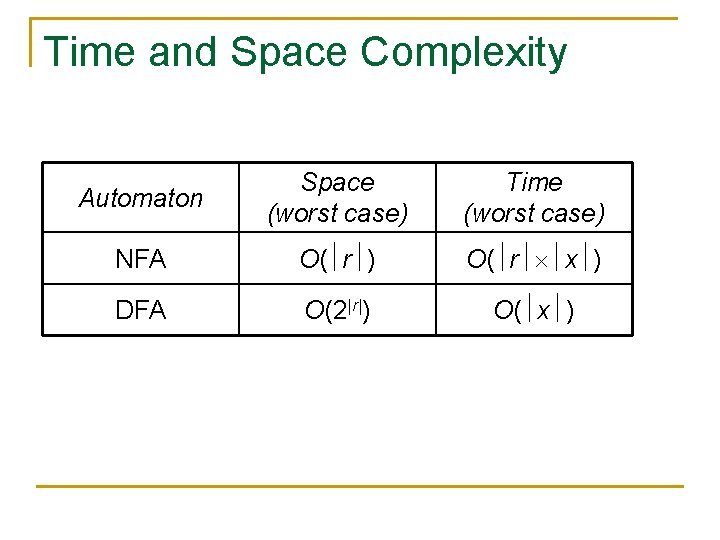
Time and Space Complexity Automaton Space (worst case) Time (worst case) NFA O( r ) O( r x ) DFA O(2|r|) O( x )