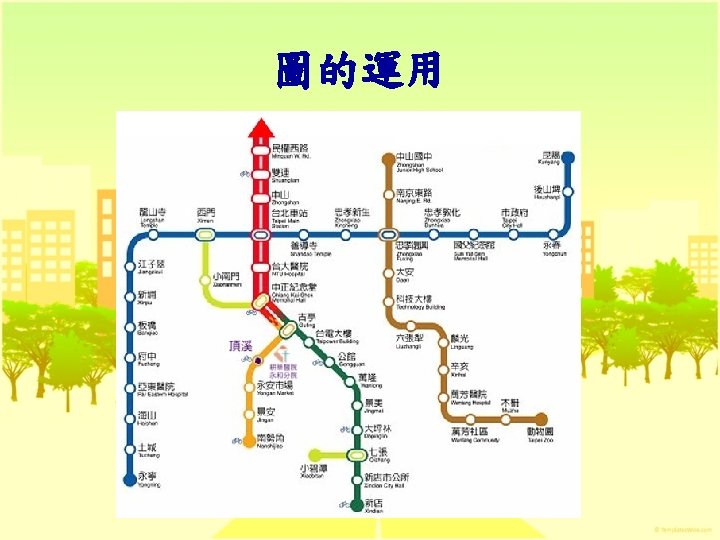
Chapter 6 Graph Chang ChiChung 2011 17 Graph

Chapter 6 Graph Chang Chi-Chung 2011. 17

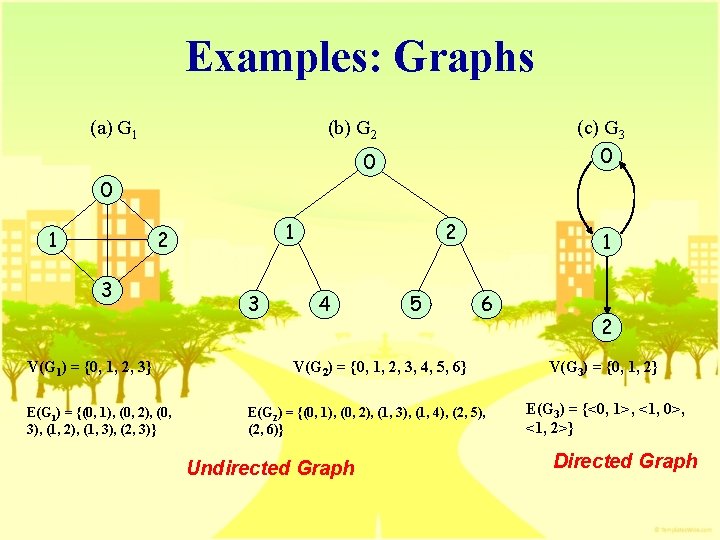
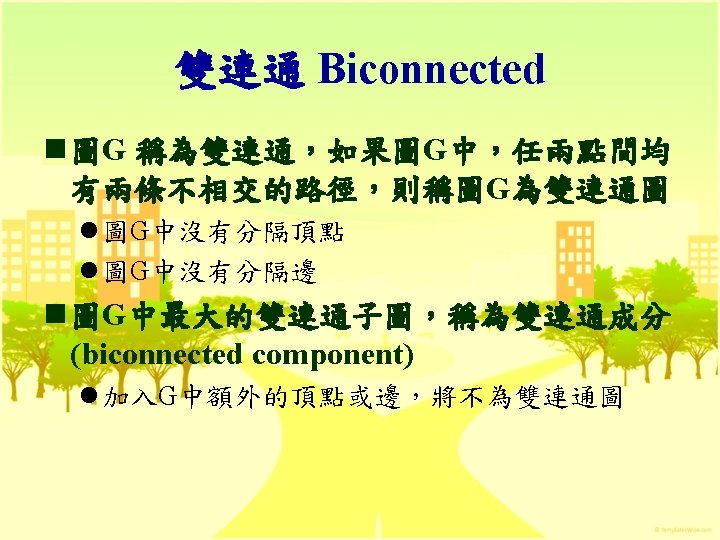
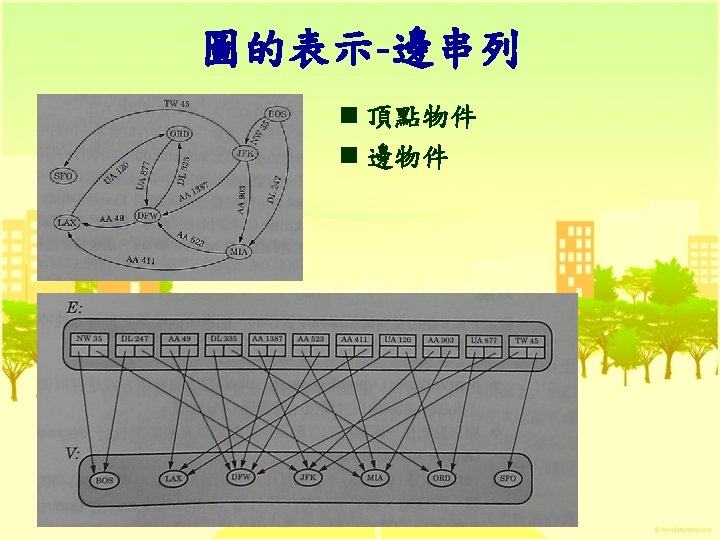
Graph n 圖(graph) 的定義 G = (V, E) l V為頂點的集合 l E為邊的集合，以頂點對表示 n 有向圖和無向圖 l Undirected graph (graph) edge (u, v) = (v, u) l Directed graph (digraph) edge <u, v> ≠ <v, u>

Examples: Graphs (a) G 1 (b) G 2 (c) G 3 0 0 0 1 1 2 3 V(G 1) = {0, 1, 2, 3} E(G 1) = {(0, 1), (0, 2), (0, 3), (1, 2), (1, 3), (2, 3)} 3 2 4 5 1 6 V(G 2) = {0, 1, 2, 3, 4, 5, 6} E(G 2) = {(0, 1), (0, 2), (1, 3), (1, 4), (2, 5), (2, 6)} Undirected Graph 2 V(G 3) = {0, 1, 2} E(G 3) = {<0, 1>, <1, 0>, <1, 2>} Directed Graph

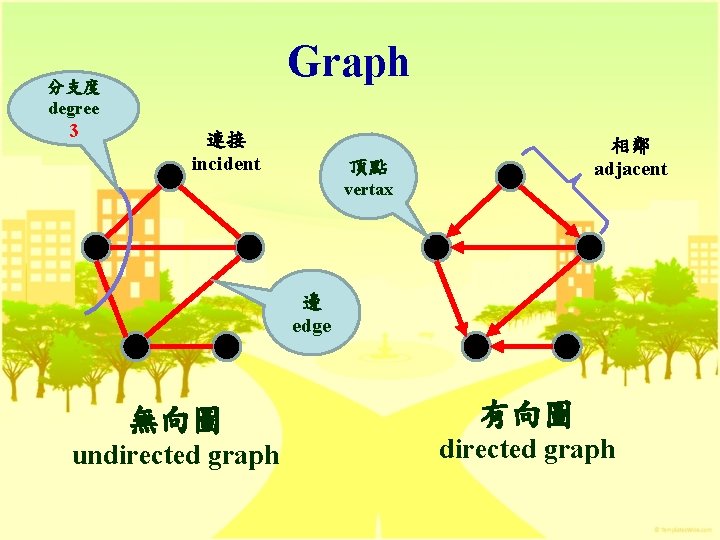
Graph 分支度 degree 3 連接 incident 相鄰 adjacent 頂點 vertax 邊 edge 無向圖 undirected graph 有向圖 directed graph

Simple Graph n No self edges (self loops，自我迴路) l A graph may not have an edge from a vertex, v, back to itself. n No multiple edges (多重邊或平行邊) l A graph may not have multiple occurrences of same edges. 0 0 1 1 2 (a) Graph with a self edge 3 2 (b) Multigraph

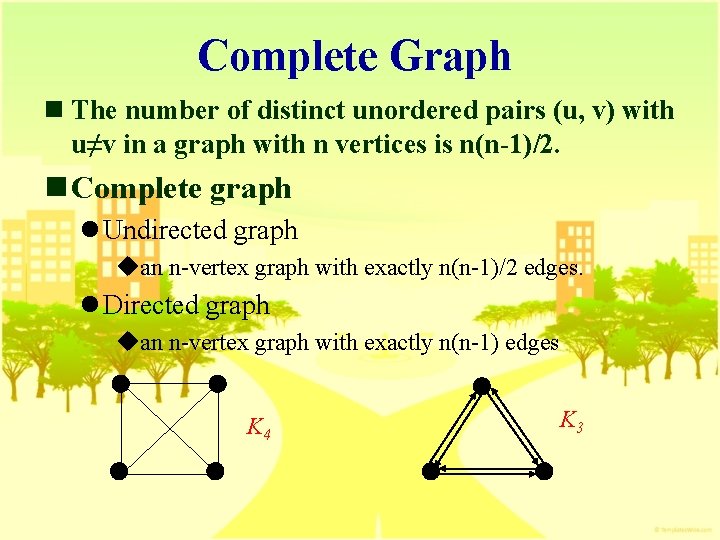
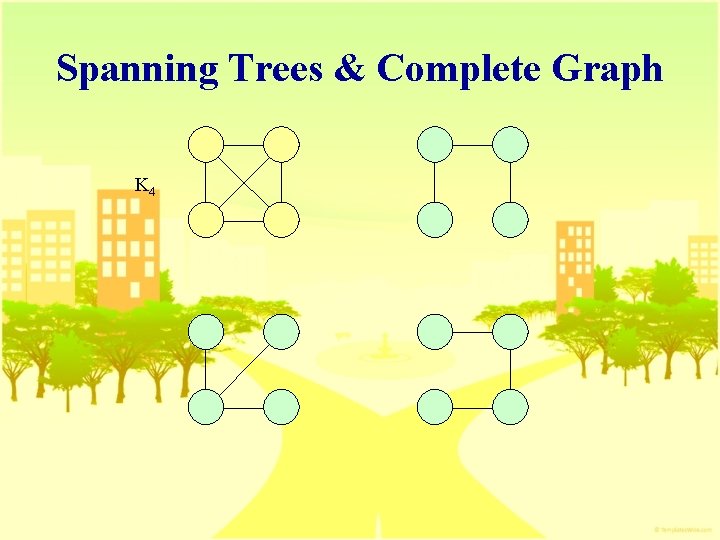
Complete Graph n The number of distinct unordered pairs (u, v) with u≠v in a graph with n vertices is n(n-1)/2. n Complete graph l Undirected graph uan n-vertex graph with exactly n(n-1)/2 edges. l Directed graph uan n-vertex graph with exactly n(n-1) edges K 4 K 3

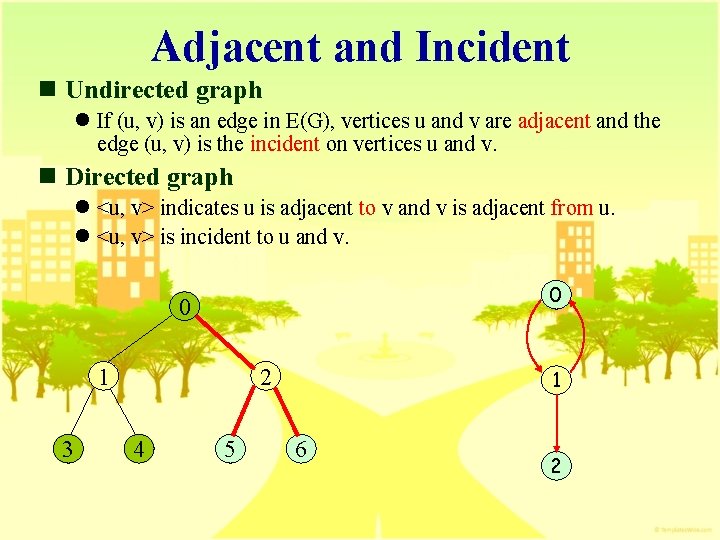
Adjacent and Incident n Undirected graph l If (u, v) is an edge in E(G), vertices u and v are adjacent and the edge (u, v) is the incident on vertices u and v. n Directed graph l <u, v> indicates u is adjacent to v and v is adjacent from u. l <u, v> is incident to u and v. 0 0 1 3 2 4 5 1 6 2

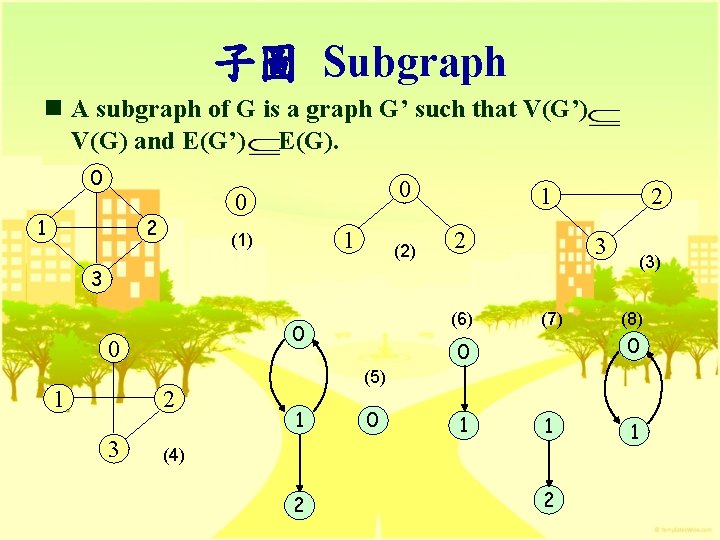
子圖 Subgraph n A subgraph of G is a graph G’ such that V(G’) V(G) and E(G’) E(G). 0 1 0 0 2 1 (1) (2) 1 2 2 3 (3) 3 0 0 1 2 3 (6) (7) (8) 0 0 (5) 1 0 1 1 (4) 2 2 1

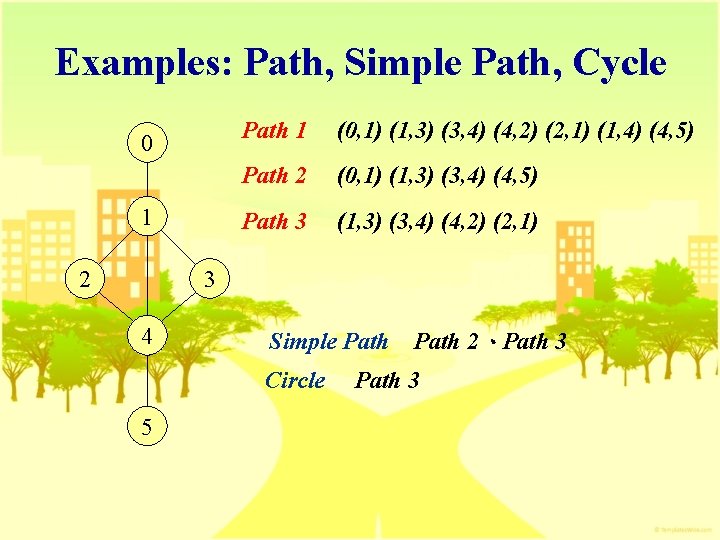
Path and Length n Path l A path from vertex u to vertex v in graph G is a sequence of vertices u, i 1, i 2, …, ik, v, such that (u, i 1), (i 1, i 2), …, (ik, v) are edges in E(G). l G’ is directed graph, <u, i 1>, <i 1, i 2>, …, <ik, v> are edges in E(G’). n Length l The length of a path is the number of edges on it. n Simple Path l A simple path is a path in which all vertices except possibly the first and last are distinct. n A path (0, 1), (1, 3), (3, 2) can be written as 0, 1, 3, 2.

Cycle n A cycle is a simple path in which the first and last vertices are the same. n Similar definitions of path and cycle can be applied to directed graphs.

Examples: Path, Simple Path, Cycle 0 1 2 Path 1 (0, 1) (1, 3) (3, 4) (4, 2) (2, 1) (1, 4) (4, 5) Path 2 (0, 1) (1, 3) (3, 4) (4, 5) Path 3 (1, 3) (3, 4) (4, 2) (2, 1) 3 4 Simple Path Circle 5 Path 2、Path 3

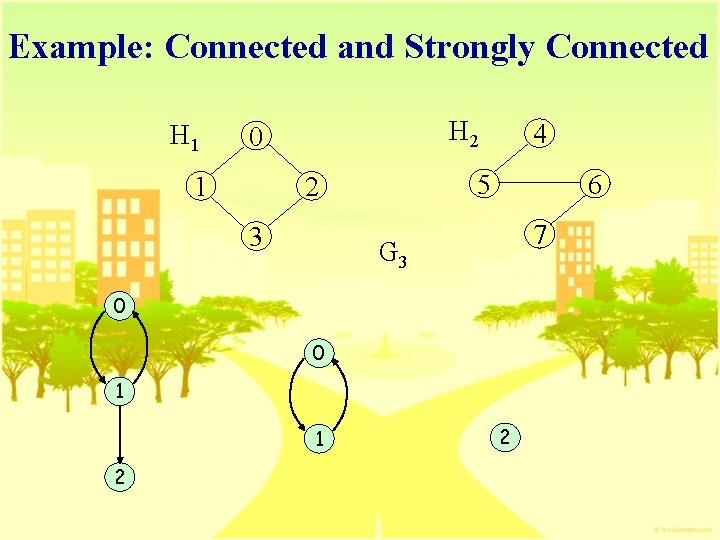
Example: Connected and Strongly Connected H 1 H 2 0 1 5 2 3 4 6 7 G 3 0 0 1 1 2 2

Spanning Trees & Complete Graph K 4

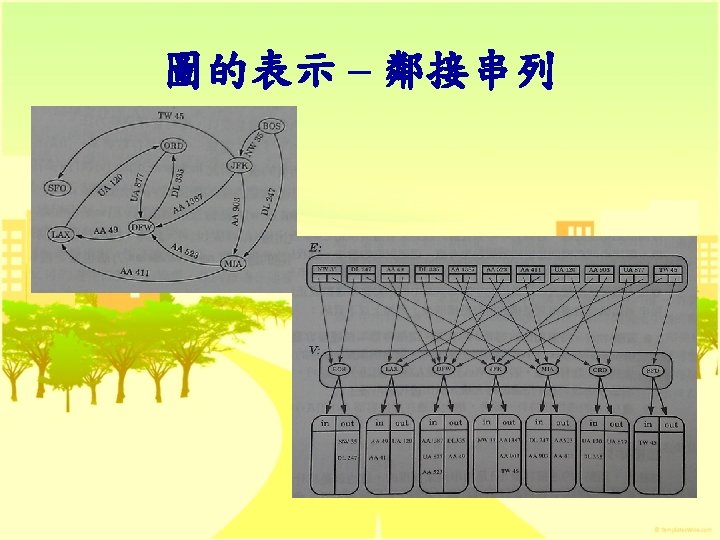
重要的觀念 n 圖的表示方法 (資料結構) l 邊串列 (edges lists) l 鄰接串列 (adjacency lists) l 鄰接矩陣 (adjacency matrix) n 圖的走訪 (traversal) l DFS (深先搜尋，depth-first search) l BFS (廣先搜尋，breadth-first search)

Adjacency Lists Head. Nodes [0 ][1 ][2 ] [3 ] 3 1 2 0 2 3 0 0 1 3 0 0 0 1 2 0 G 1 ] 1 2 3 0 Head. Nodes [0 ][1 ][2 0 1 0 2 0 0 1 0 G 2 2

Adjacency Lists H 1 Head. Nodes [0 ][1 ][2 ] [3 ][4 ][5 ][6 ] [7 ] 2 1 0 3 0 0 0 3 0 1 1 0 5 0 6 4 0 5 7 0 6 0 G 3 0 1 2 3 G 3 H 2 4 5 6 7

Inverse Adjacency Lists [0 ][1 ][2 ] 0 1 0 2 0 0 0 1 2 G 2 [0] 1 0 [1] 0 0 [2] 1 0 求入分支度須用此反轉串列

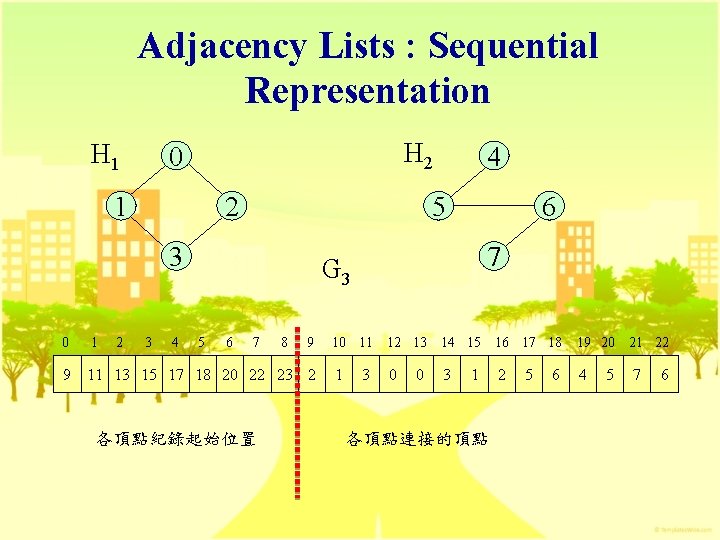
Adjacency Lists : Sequential Representation H 1 H 2 0 1 2 5 3 0 1 2 3 4 4 6 7 G 3 5 6 7 8 9 9 11 13 15 17 18 20 22 23 2 各頂點紀錄起始位置 10 11 12 13 14 15 16 17 18 19 20 1 0 3 4 3 0 1 各頂點連接的頂點 2 5 6 5 21 22 7 6

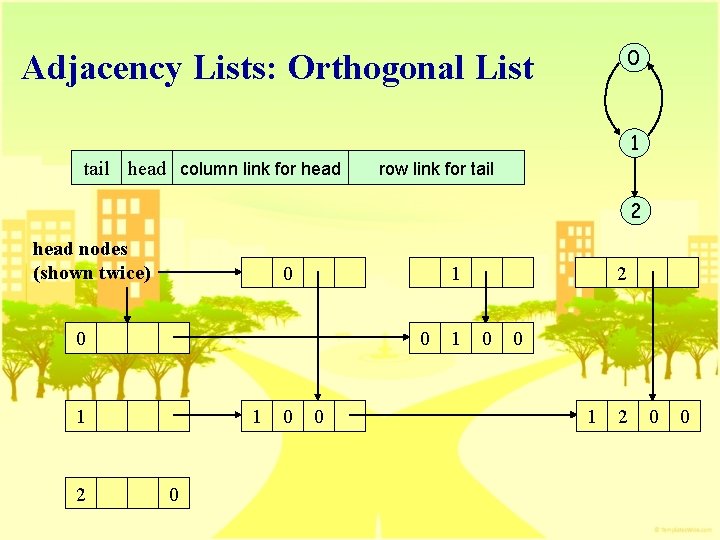
0 Adjacency Lists: Orthogonal List 1 tail head column link for head row link for tail 2 head nodes (shown twice) 0 1 0 0 1 2 1 0 0 0 1 2 0 0

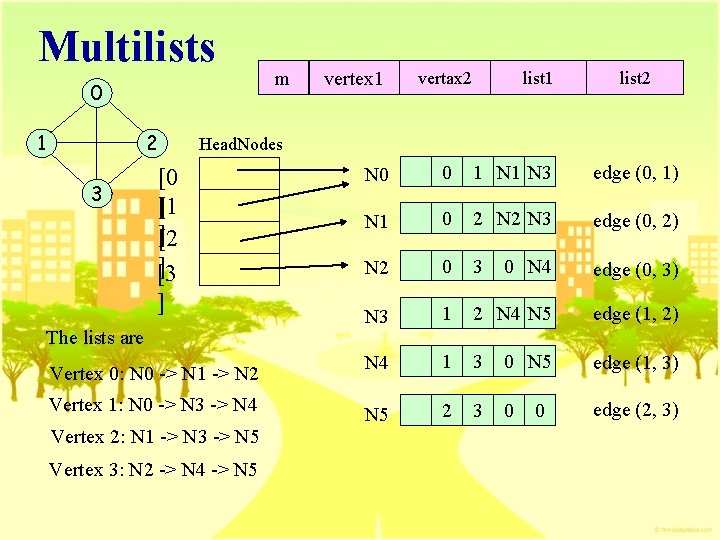
Multilists 0 1 2 3 m vertex 1 vertax 2 list 1 list 2 Head. Nodes [0 ][1 ][2 ] [3 ] The lists are Vertex 0: N 0 -> N 1 -> N 2 Vertex 1: N 0 -> N 3 -> N 4 Vertex 2: N 1 -> N 3 -> N 5 Vertex 3: N 2 -> N 4 -> N 5 N 0 0 1 N 3 edge (0, 1) N 1 0 2 N 3 edge (0, 2) N 2 0 3 0 N 4 edge (0, 3) N 3 1 2 N 4 N 5 edge (1, 2) N 4 1 3 0 N 5 edge (1, 3) N 5 2 3 0 edge (2, 3) 0

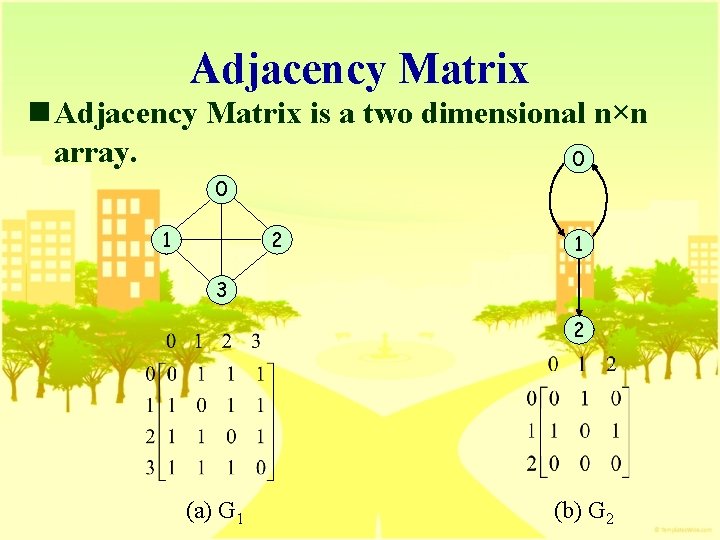
Adjacency Matrix n Adjacency Matrix is a two dimensional n×n array. 0 0 1 2 1 3 2 (a) G 1 (b) G 2

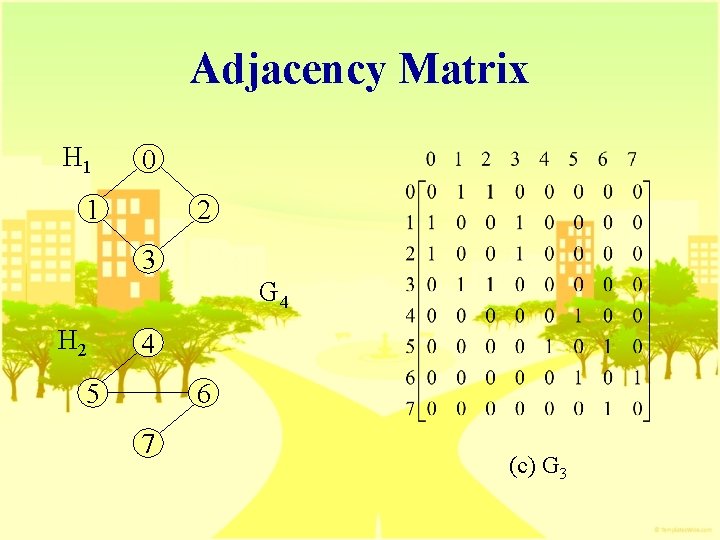
Adjacency Matrix H 1 0 1 2 3 G 4 H 2 4 5 6 7 (c) G 3

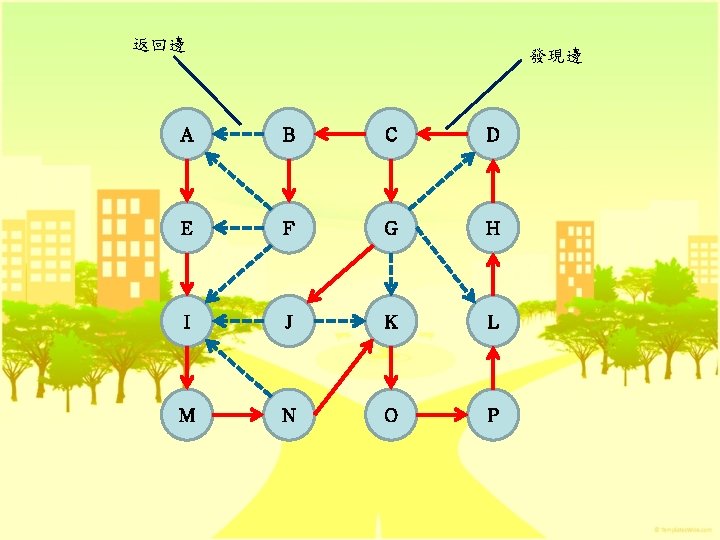
Depth-First Search 0 0, 1, 3, 7, 4, 5, 2, 6 1 3 Head. Nodes [0 ] [1 ][2 ] [3 ] [4 ] [5 ] [6 ] [7] 1 0 0 1 1 2 2 3 5 7 7 4 2 4 5 7 0 4 0 6 0 0 0 5 6 0 6

DFS Algorithm DFS(G, v) Input: A graph G and a vertx v of G Output: A labeling of the edges in the connected component of v as discovery edges and back edges for all edges e in G. incident. Edges(v) do if edge e is unexplored then w G. opposite(v, e) if vertax w is unexplored then label e as a discovery edge recursively call DFS(G, w) else label e as a back edge

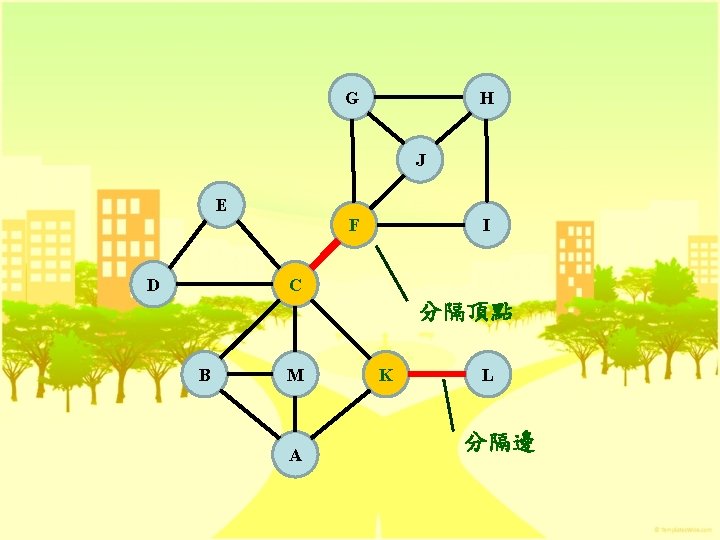
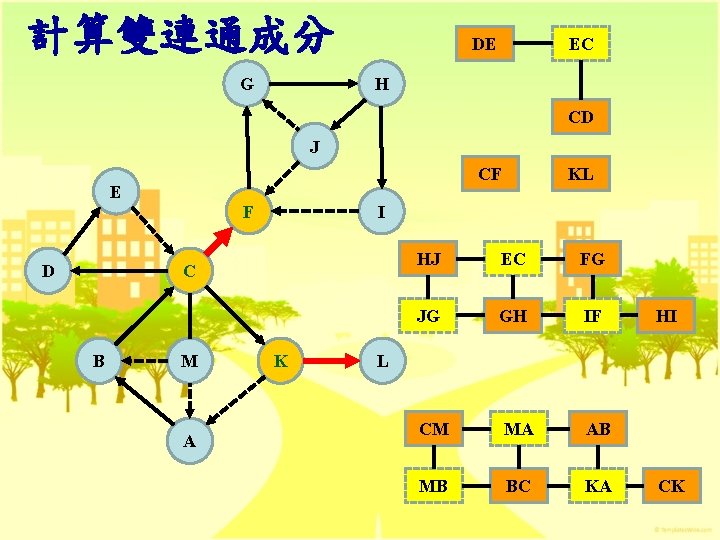
計算雙連通成分 G DE EC H CD J CF E D F I C B M A KL K HJ EC FG JG GH IF CM MA AB MB BC KA HI L CK

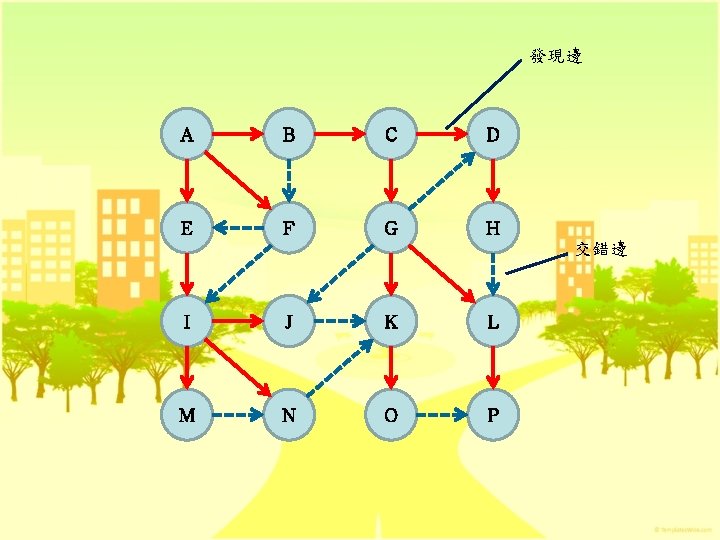
Breadth-First Search 0, 1, 2, 3, 4, 5, 6, 7 1 3 Head. Nodes [0 ] [1 ][2 ] [3 ] [4 ] [5 ] [6 ] [7] 1 0 0 1 1 2 2 3 0 2 3 5 7 7 4 2 4 5 7 0 4 0 6 0 0 0 5 6 0 6

BFS Algorithm BFS(G, v) Input: A graph G and a vertx s of G Output: A labeling of the edges in the connected component of s as discovery edges and cross edges create an empty container L 0 insert s into L 0 i 0 while Li is not empty do create an empty container Li+1 for each vertax v in Li do for all edge e in G. incident. Edges(v) do if edge e is unexplored then let w be the other endpoint of e if vertax w is unexplored then label e as a discovery edge insert w into Li+1 else label e as a cross edge i i+1