Captulo I Vectores z y x Un vector















































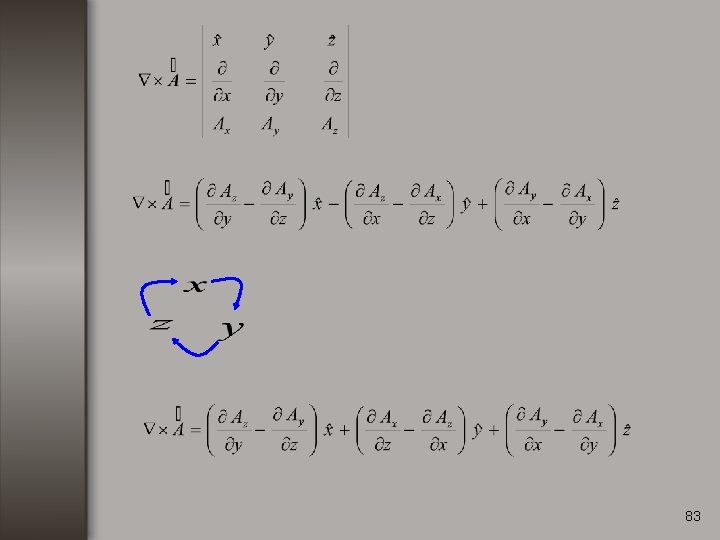




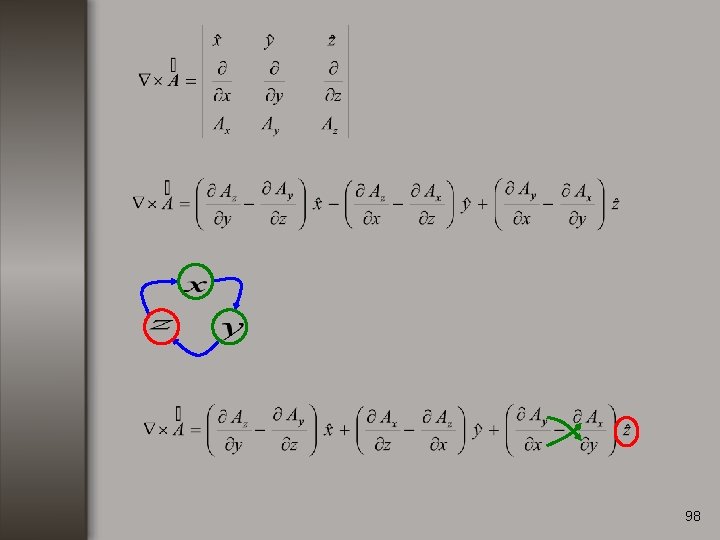


























- Slides: 131

Capítulo I. Vectores z y x Un vector puede representarse de la forma: 1

Donde son los vectores unitarios en las direcciones de los ejes “x”, “y” y “z” respectivamente. son las componentes escalares del vector y x 2

El módulo de lo encontramos usando: Vector unitario: Un vector unitario en la dirección de se define como: 3

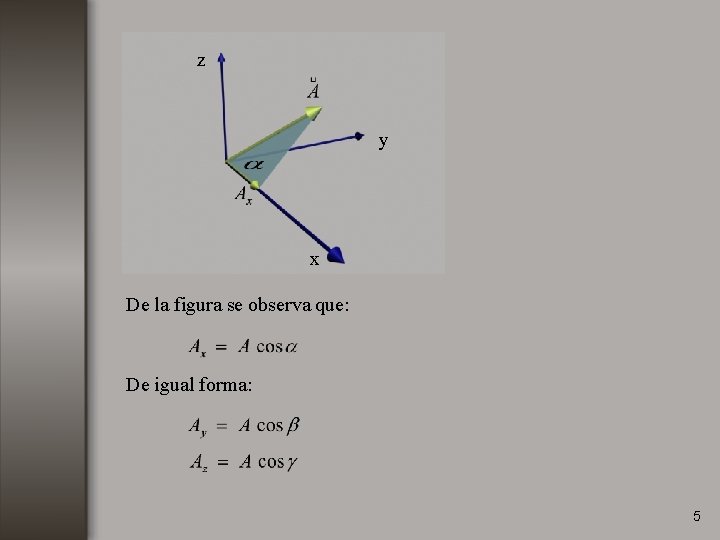
Angulos directores: Son los ángulos que forma el vector con cada uno de los ejes z y x 4

z y x De la figura se observa que: De igual forma: 5

Los cosenos directores se definen como: 6

Vector de posición: y P x 7

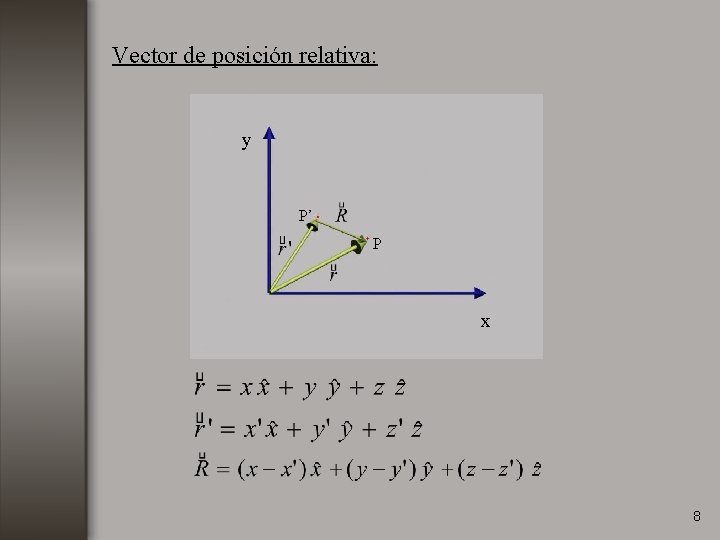
Vector de posición relativa: y P’ P x 8

Producto escalar: Sean dos vectores A y B: Entonces: 9

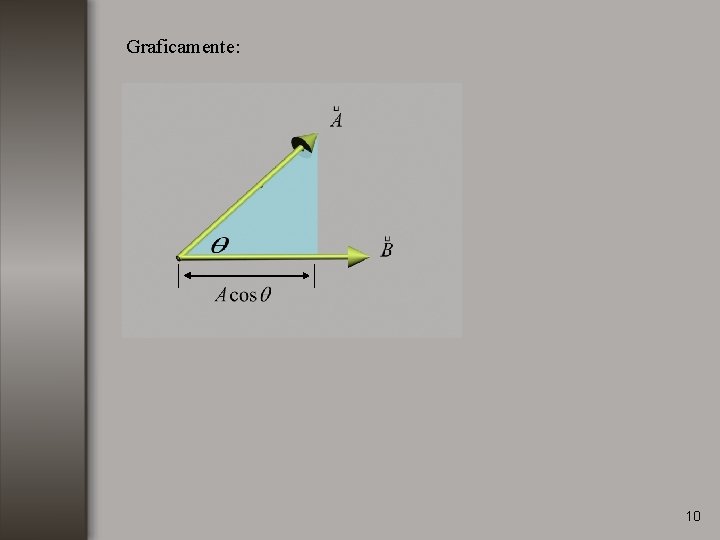
Graficamente: 10

Producto escalar de vectores unitarios: Si es un vector unitario en una dirección determinada, entonces la componente de en esa direccion es: 11

Algunas propiedades del producto escalar: 12

Producto vectorial: Sean dos vectores A y B: Entonces: 13

Producto vectorial: 14

Producto vectorial: 15

Producto vectorial: Ademas: 16

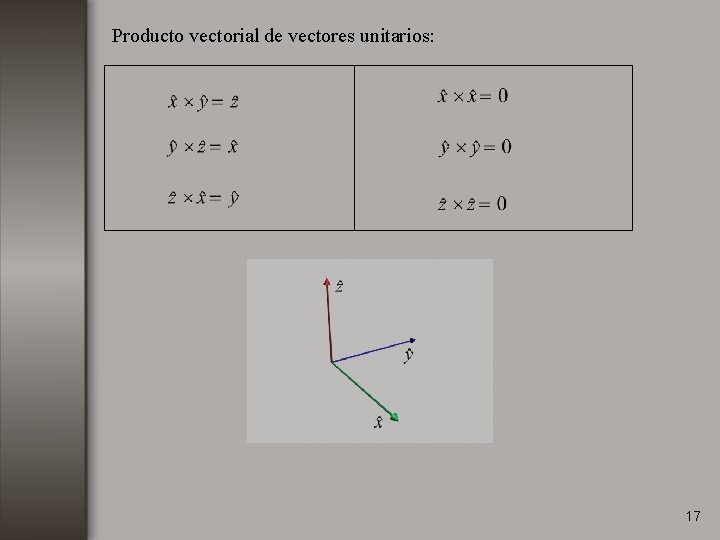
Producto vectorial de vectores unitarios: 17

Algunas propiedades del producto vectorial: Atrás del taxi 18

Campo vectorial. Velocidad del viento en un huracán 19

Campo escalar Valor de la presión atmosférica en un huracán 20

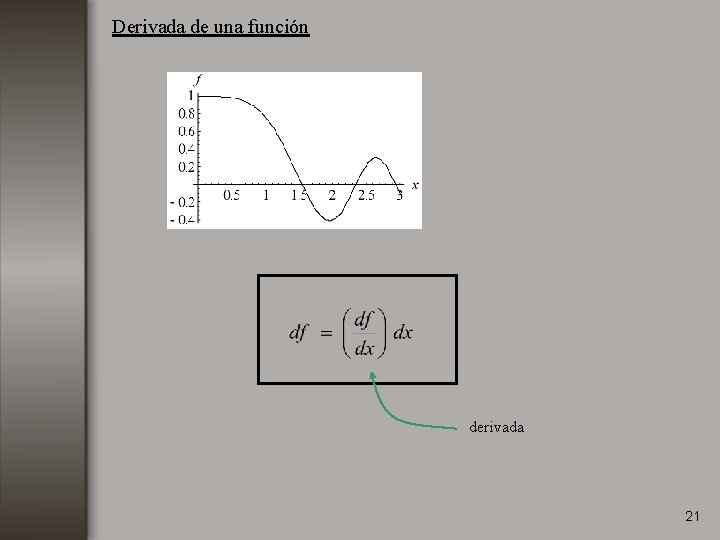
Derivada de una función derivada 21

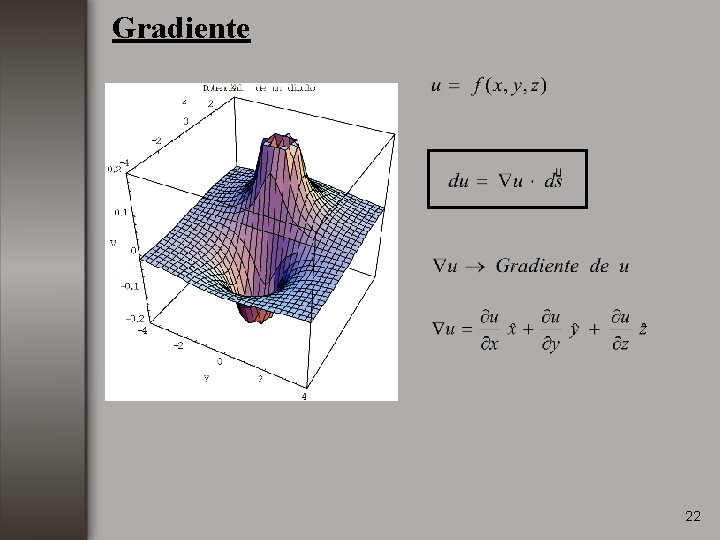
Gradiente 22

Gradiente de una función escalar 23

Gradiente de una función escalar 24

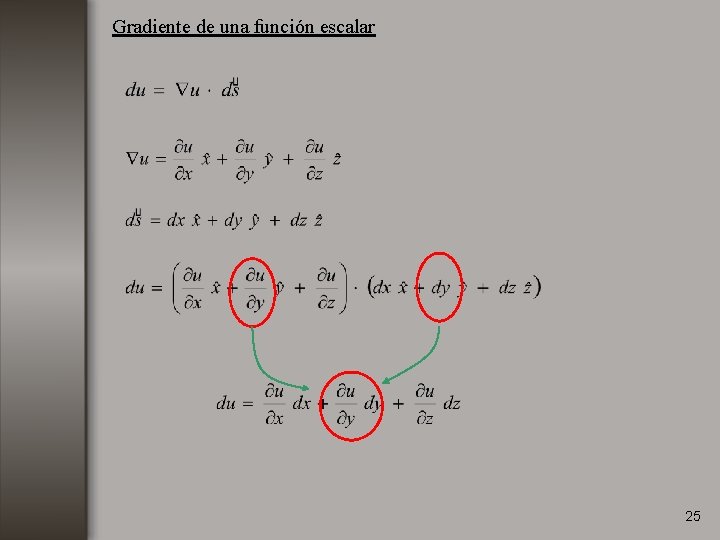
Gradiente de una función escalar 25

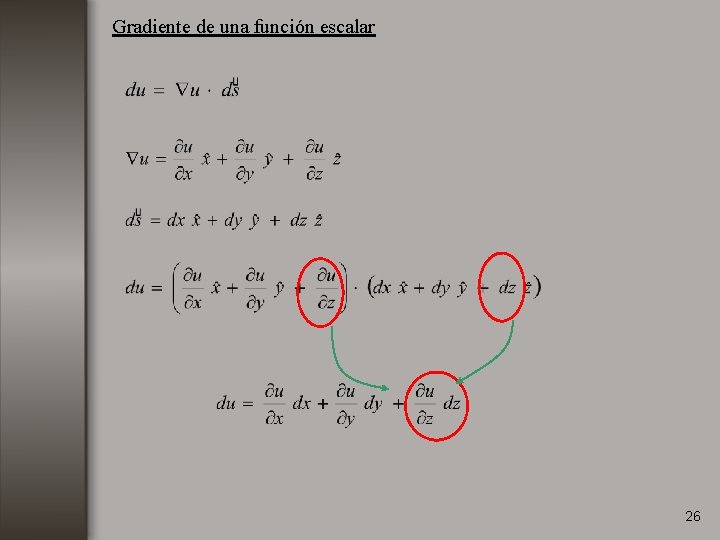
Gradiente de una función escalar 26

Gradiente de una función escalar 27

Propiedades importantes del Gradiente • Se aplica a funciones escalares • El gradiente de una función es un vector • El gradiente apunta en la dirección de máximo cambio de la función 28

¿ Qué información tendremos al calcular el gradiente de la presión en este caso? 29

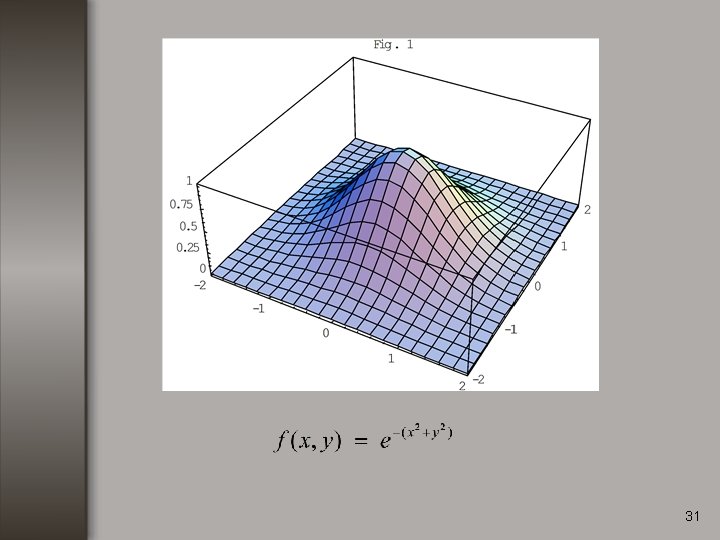
Ejemplo no. 1 Calcular el gradiente de la función: 30

31

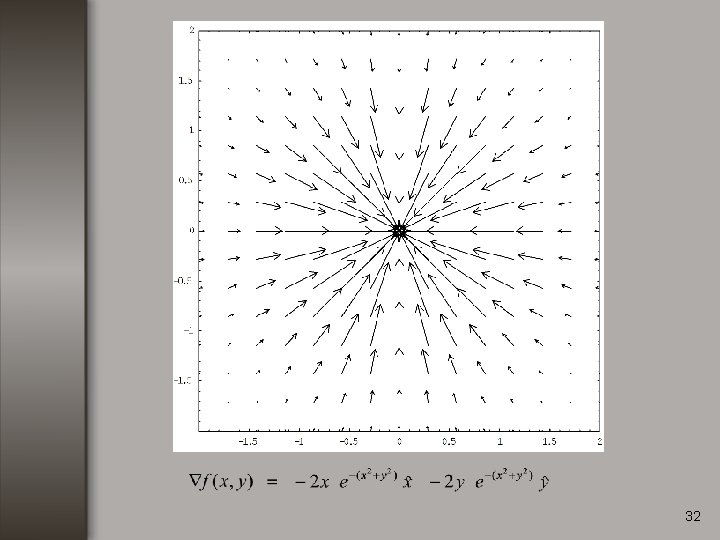
32

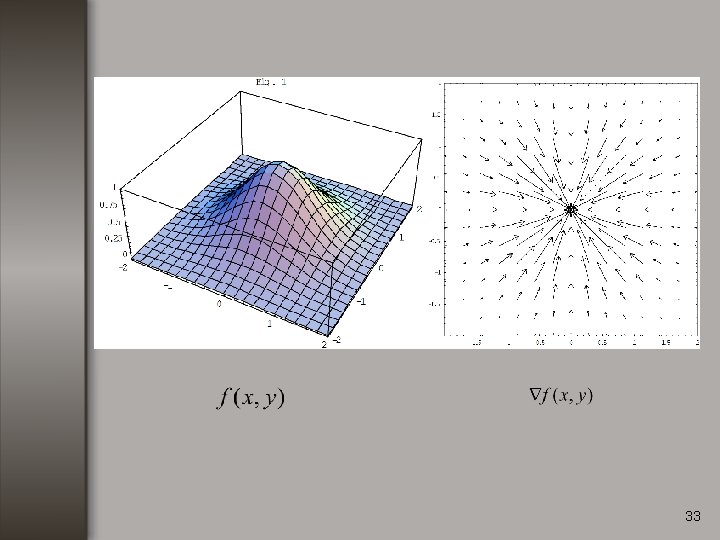
33

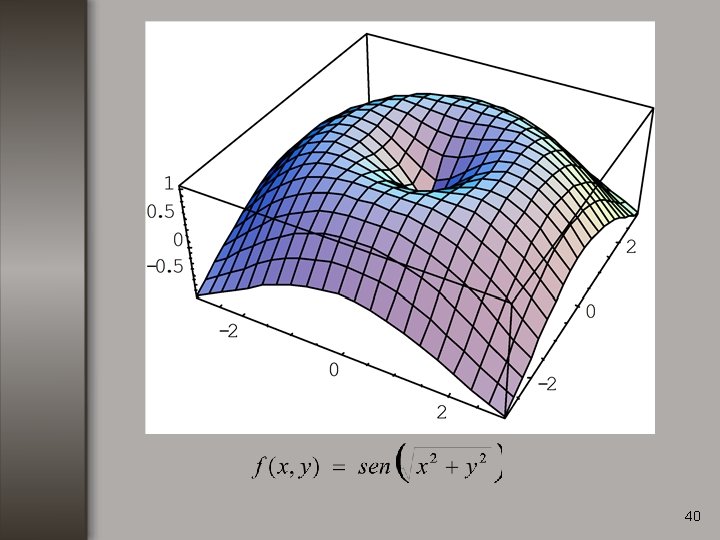
Ejemplo no. 2 Calcular el gradiente de la función: 34

Ejemplo no. 2 Calcular el gradiente de la función: 35

Ejemplo no. 2 Calcular el gradiente de la función: 36

Ejemplo no. 2 Calcular el gradiente de la función: 37

Ejemplo no. 2 Calcular el gradiente de la función: 38

Ejemplo no. 2 Calcular el gradiente de la función: 39

40

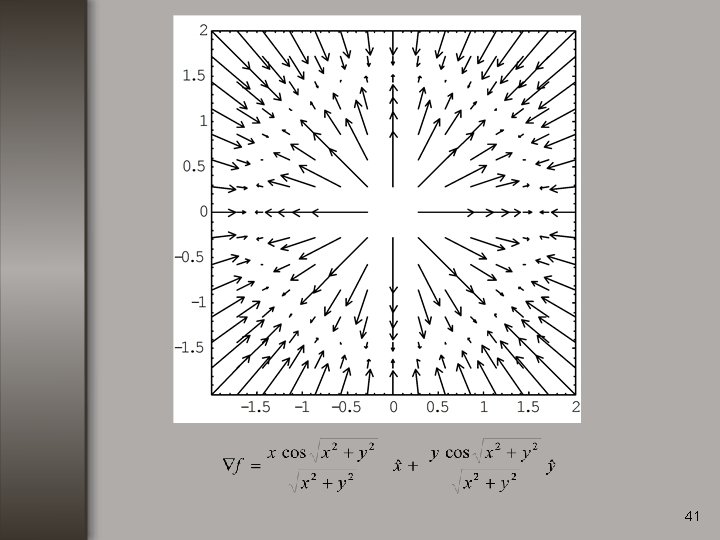
41

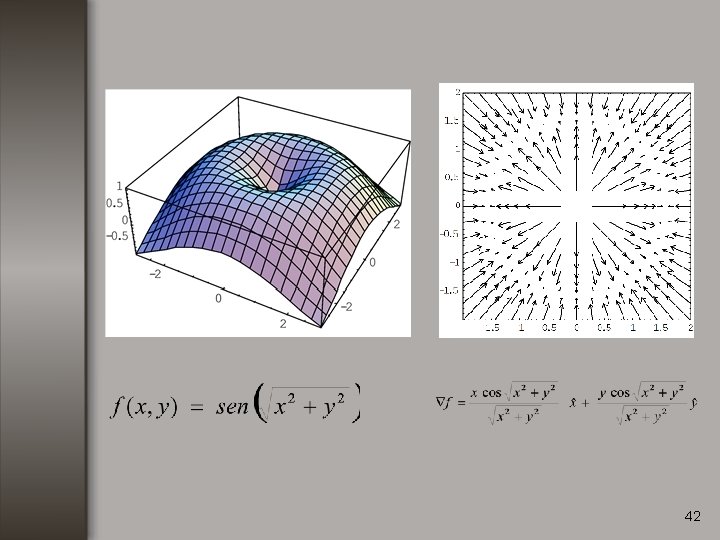
42

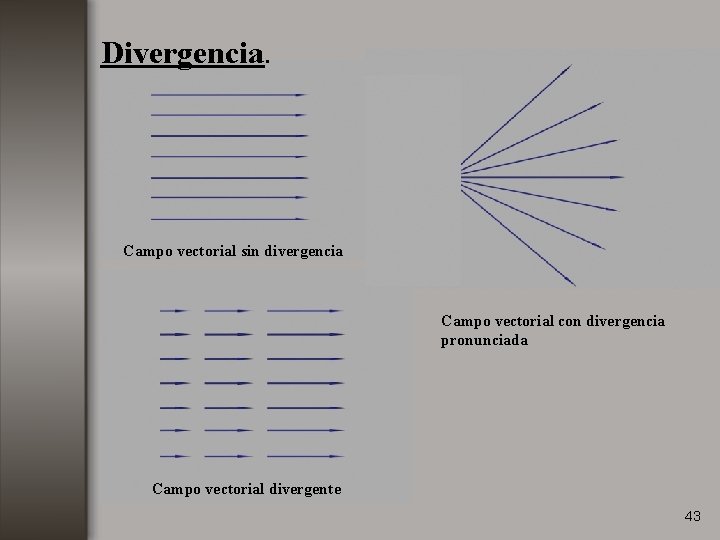
Divergencia. Campo vectorial sin divergencia Campo vectorial con divergencia pronunciada Campo vectorial divergente 43

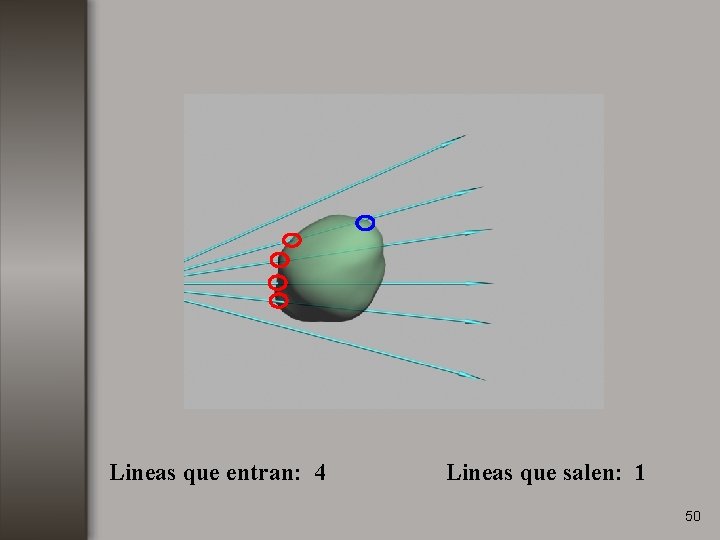
La divergencia calculada sobre un volumen, es diferente de cero si el número de líneas de campo que entran al volumen no es igual al número de líneas que salen. Campo vectorial con divergencia pronunciada 44

Conteo de líneas: una línea que entra al volumen la vamos a considerar negativa, si sale la consideraremos positiva 45

Lineas que entran: 1 46

Lineas que entran: 2 47

Lineas que entran: 3 48

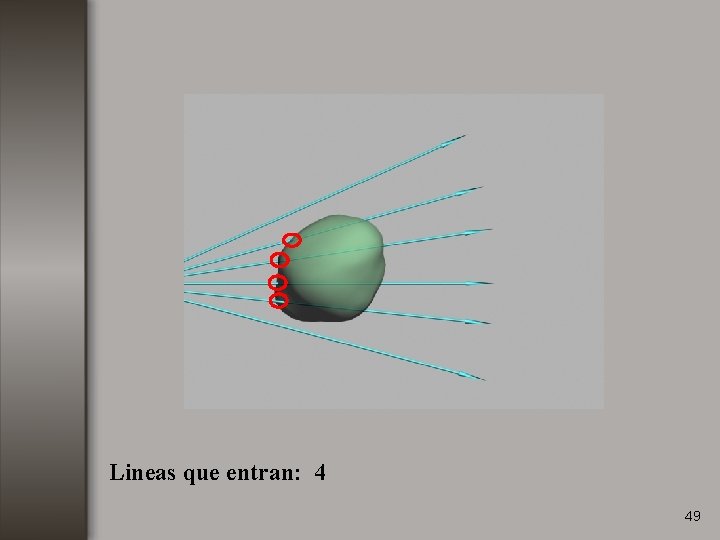
Lineas que entran: 4 49

Lineas que entran: 4 Lineas que salen: 1 50

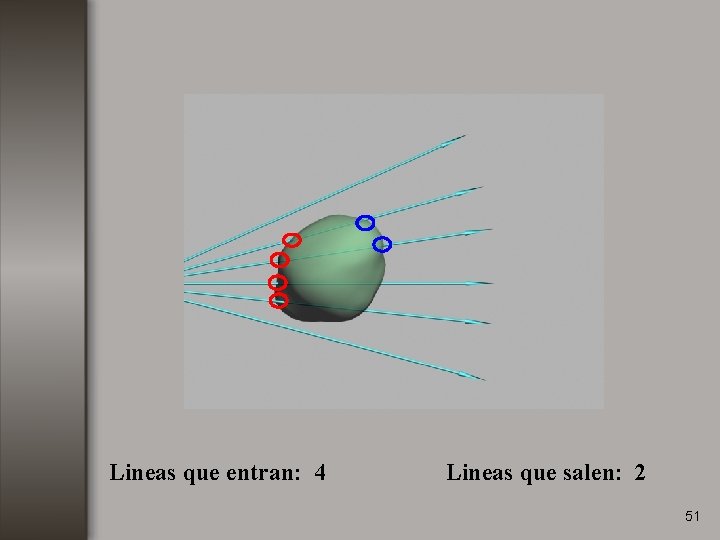
Lineas que entran: 4 Lineas que salen: 2 51

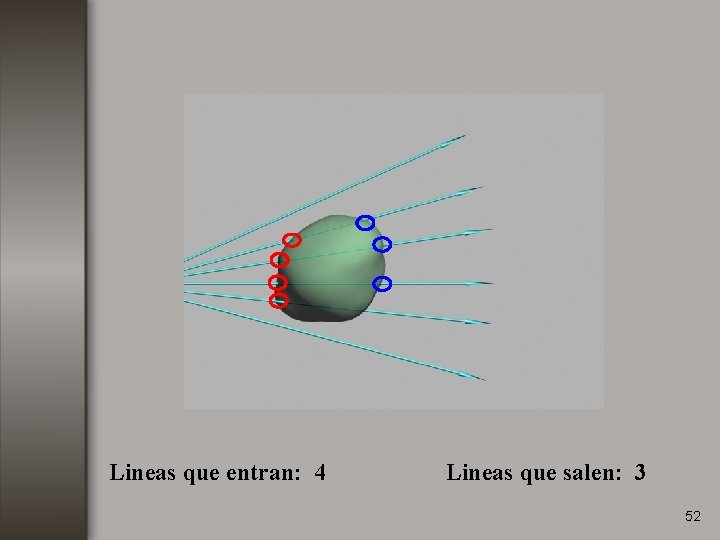
Lineas que entran: 4 Lineas que salen: 3 52

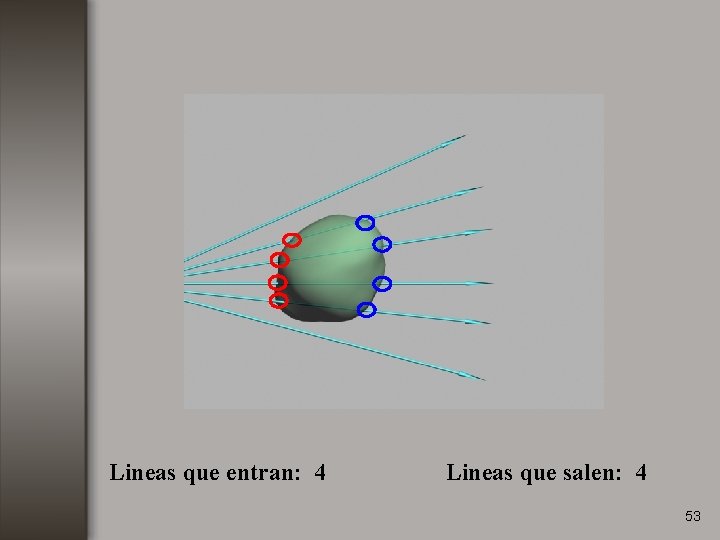
Lineas que entran: 4 Lineas que salen: 4 53

La divergencia sobre el volumen es cero. 54

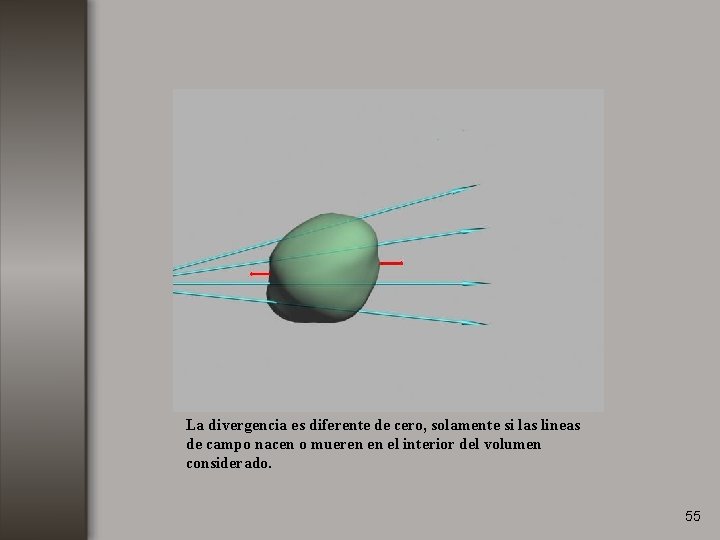
La divergencia es diferente de cero, solamente si las lineas de campo nacen o mueren en el interior del volumen considerado. 55

La divergencia sobre el volumen es diferente de cero. 56

Divergencia. Consideremos una función vectorial de la forma: La divergencia de se calcula de la siguiente manera: 57

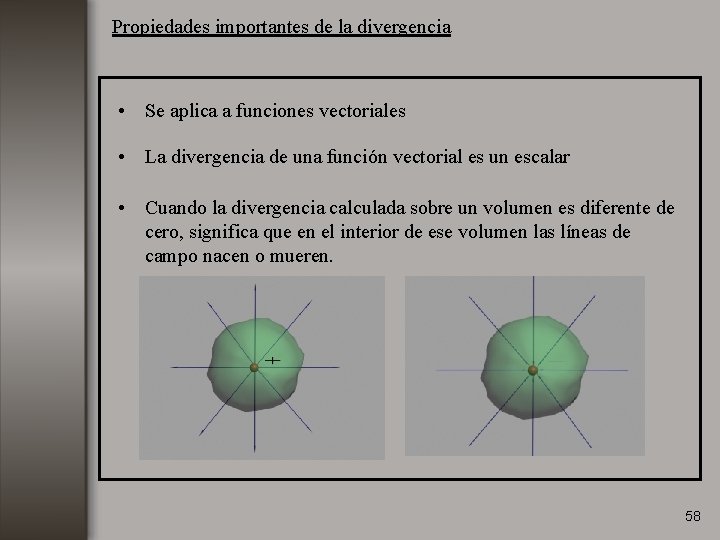
Propiedades importantes de la divergencia • Se aplica a funciones vectoriales • La divergencia de una función vectorial es un escalar • Cuando la divergencia calculada sobre un volumen es diferente de cero, significa que en el interior de ese volumen las líneas de campo nacen o mueren. 58

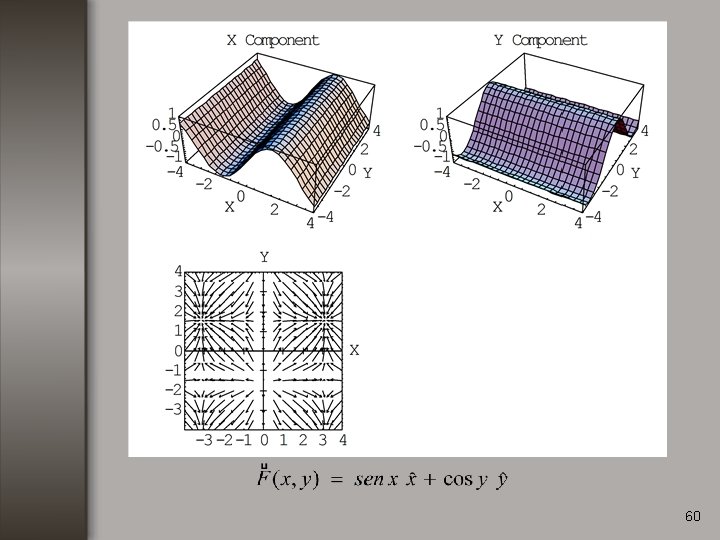
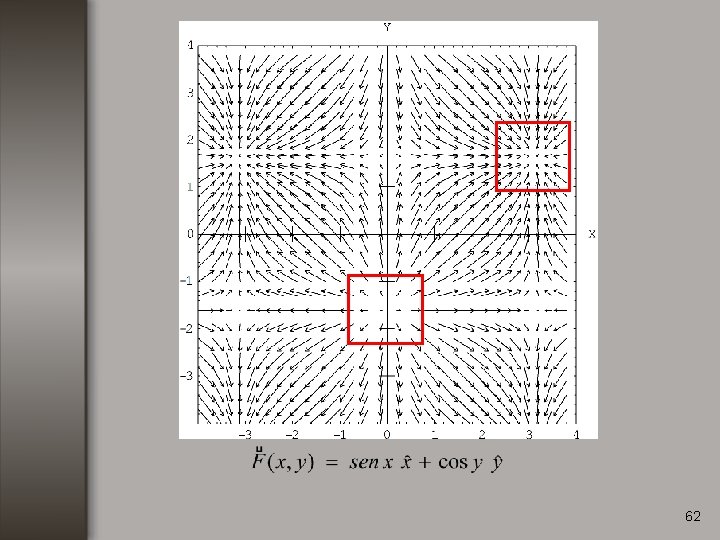
Ejemplo no. 1 Calcular la divergencia de la función: 59

60

61

62

63

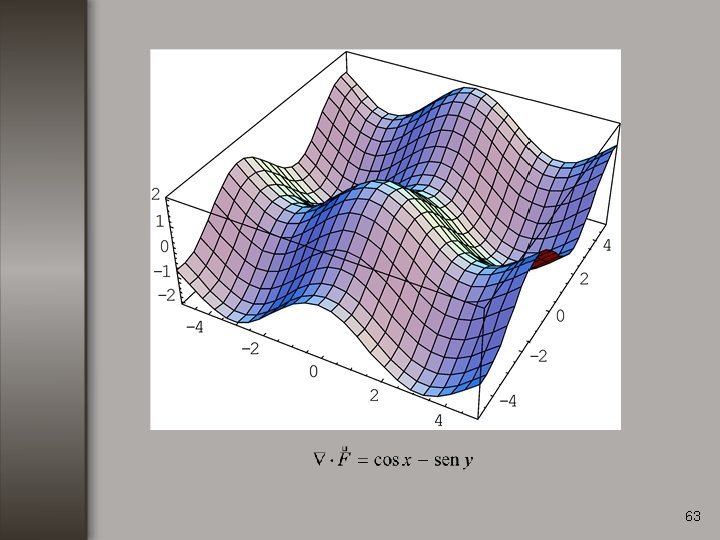
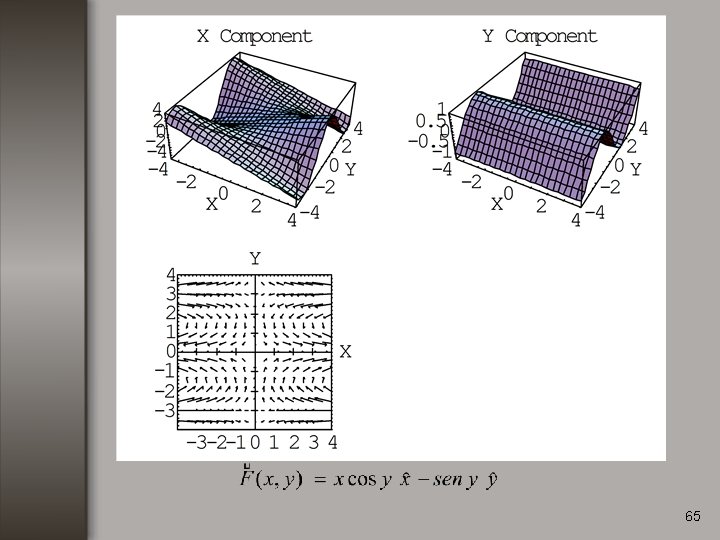
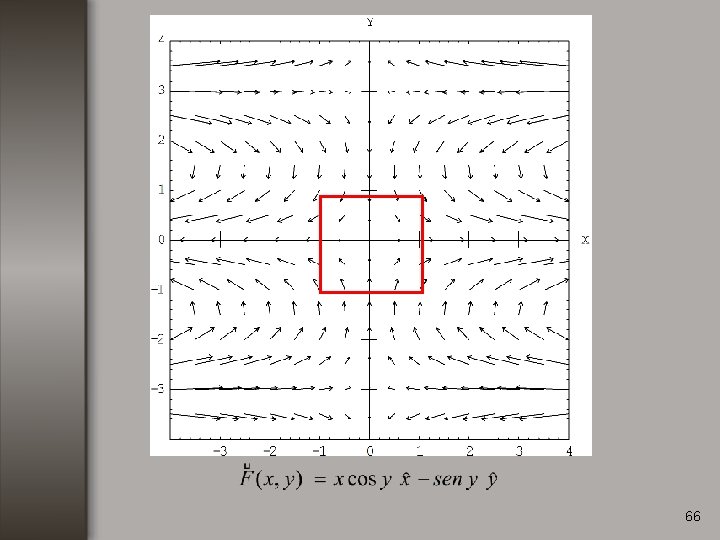
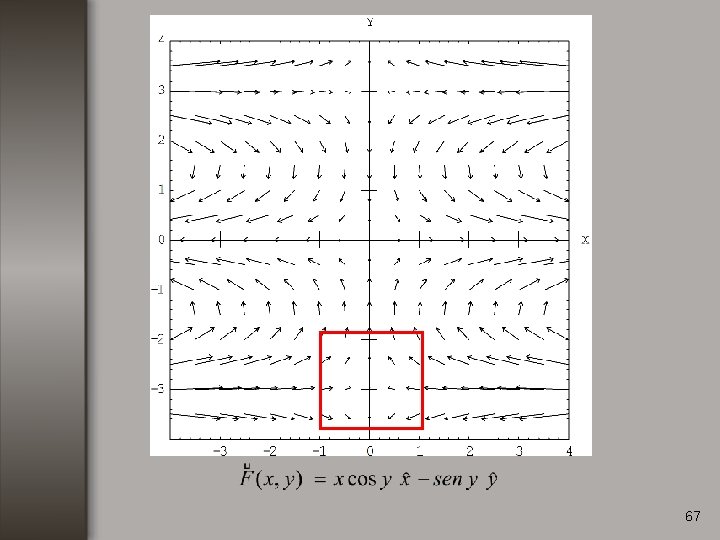
Ejemplo no. 2 Calcular la divergencia de la función: 64

65

66

67

68

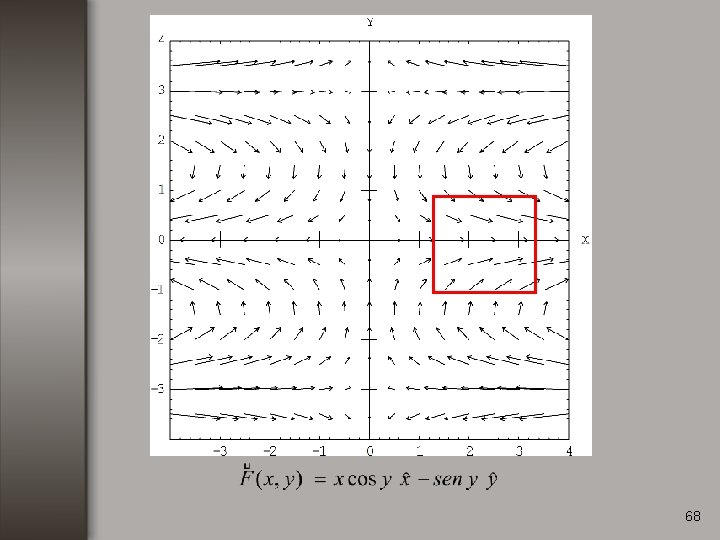
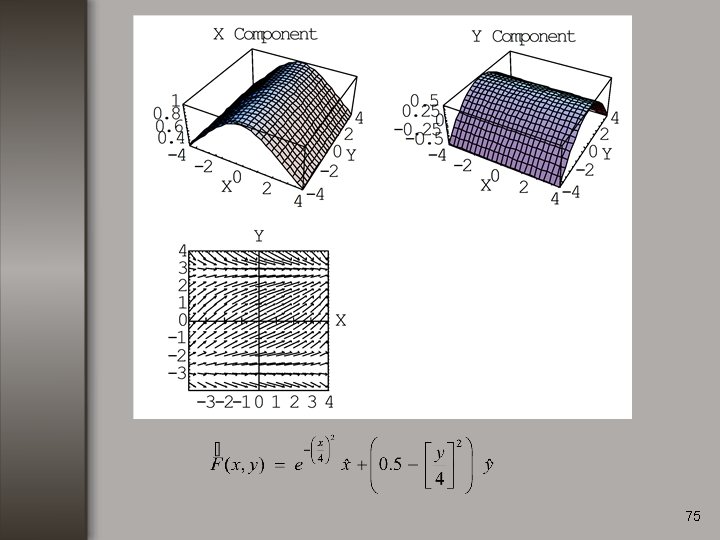
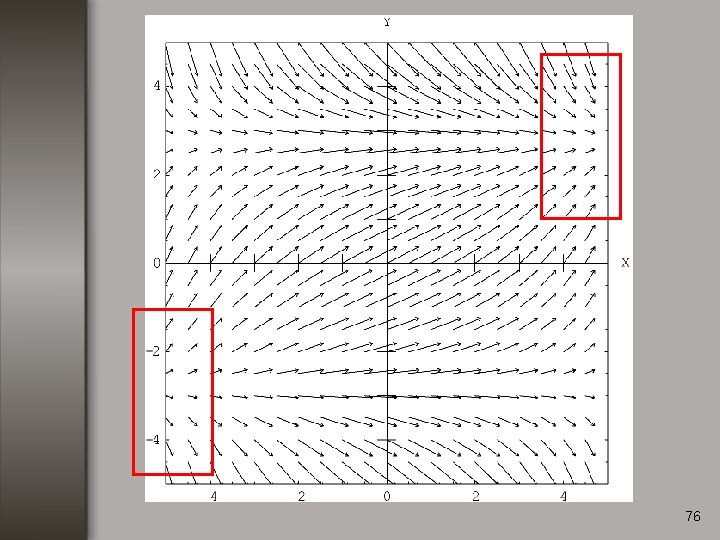
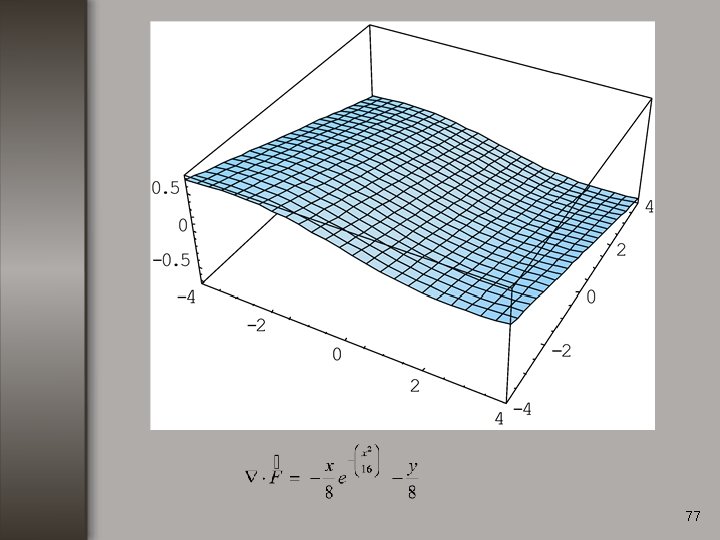
Ejemplo no. 3 Calcular la divergencia de la función: 69

Ejemplo no. 3 Calcular la divergencia de la función: 70

Ejemplo no. 3 Calcular la divergencia de la función: 71

Ejemplo no. 3 Calcular la divergencia de la función: 72

Ejemplo no. 3 Calcular la divergencia de la función: 73

Ejemplo no. 3 Calcular la divergencia de la función: 74

75

76

77

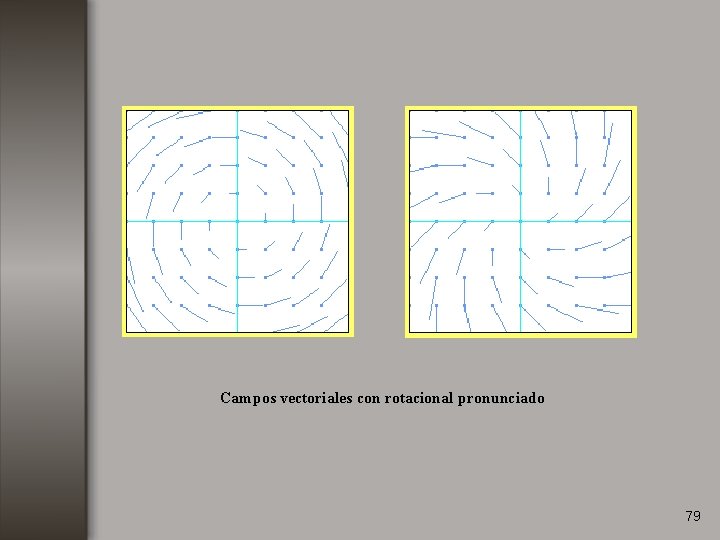
Rotacional. El rotacional de un campo vectorial mide la circulación del campo 78

Campos vectoriales con rotacional pronunciado 79

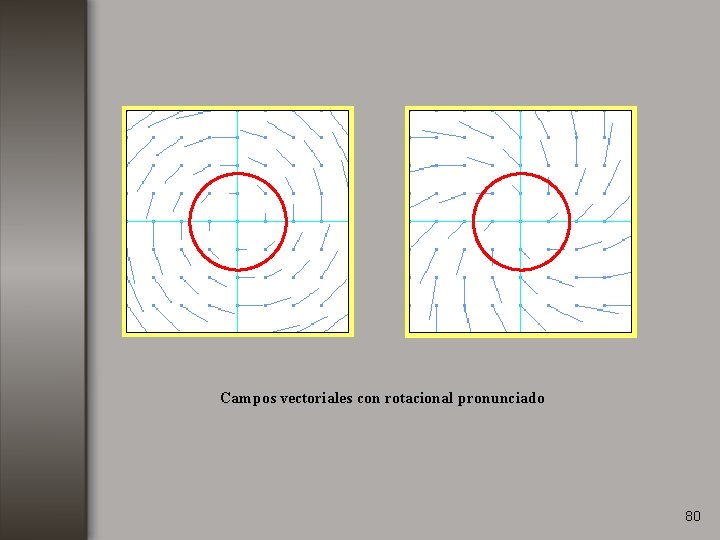
Campos vectoriales con rotacional pronunciado 80

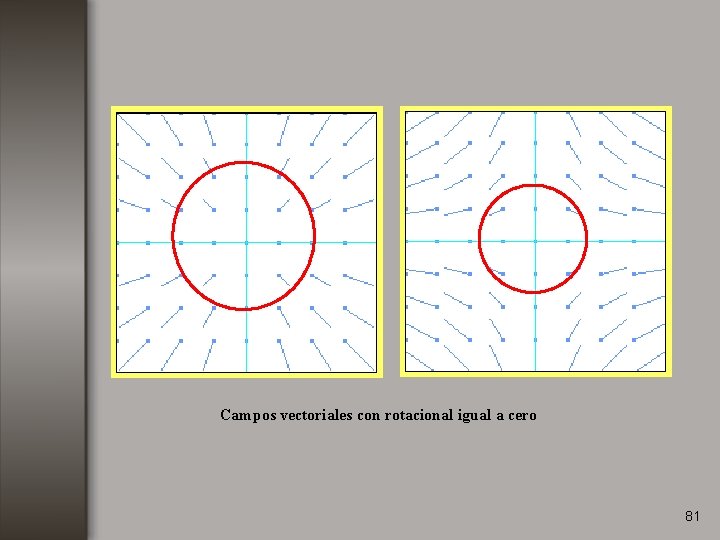
Campos vectoriales con rotacional igual a cero 81

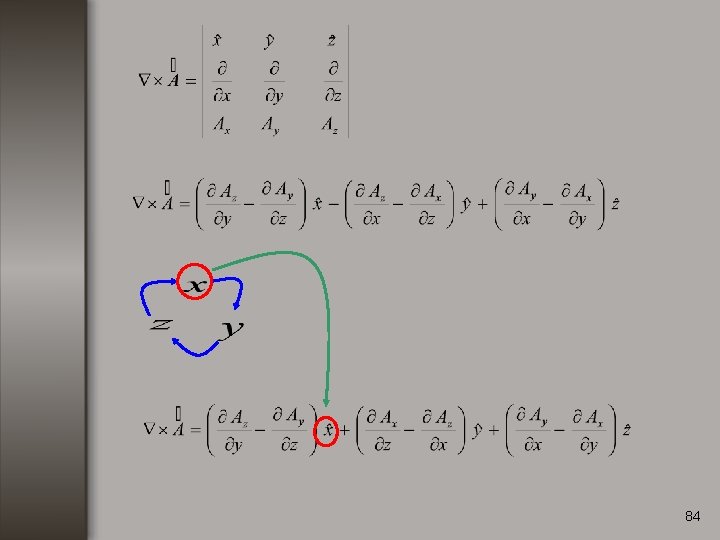
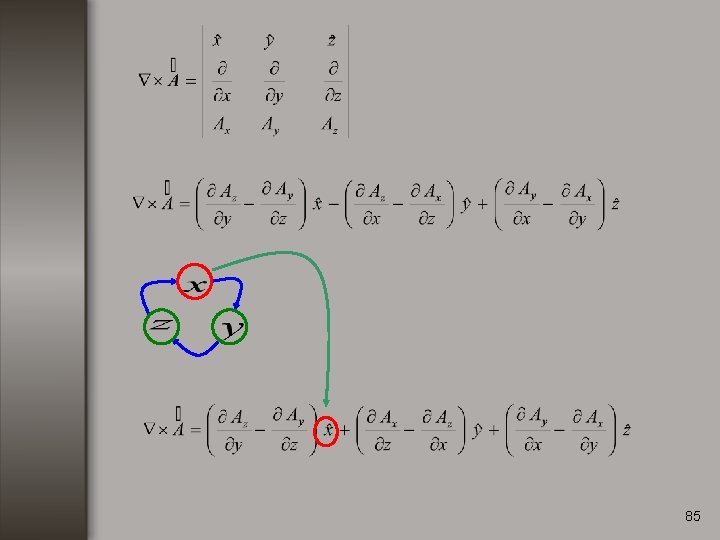
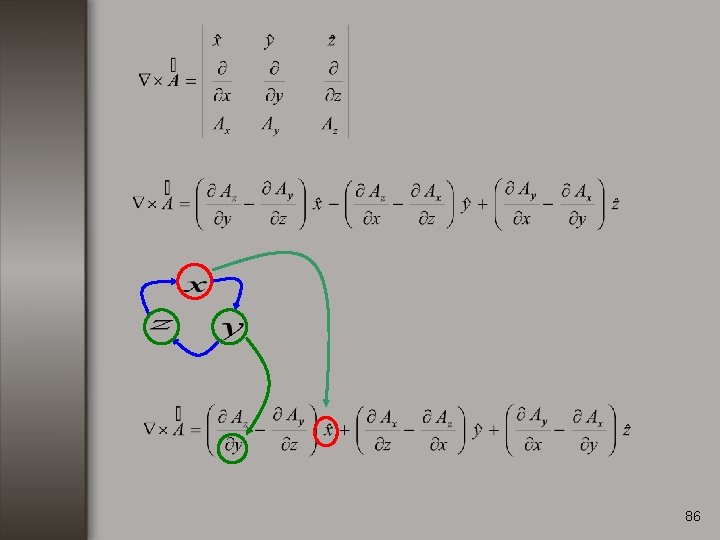
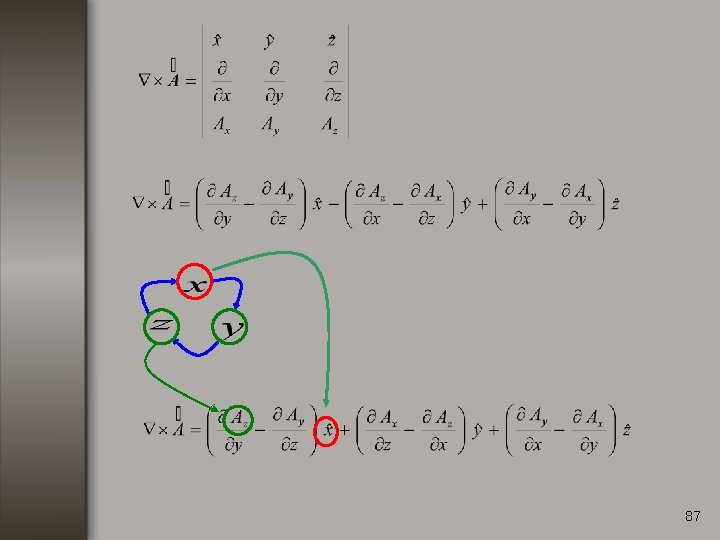
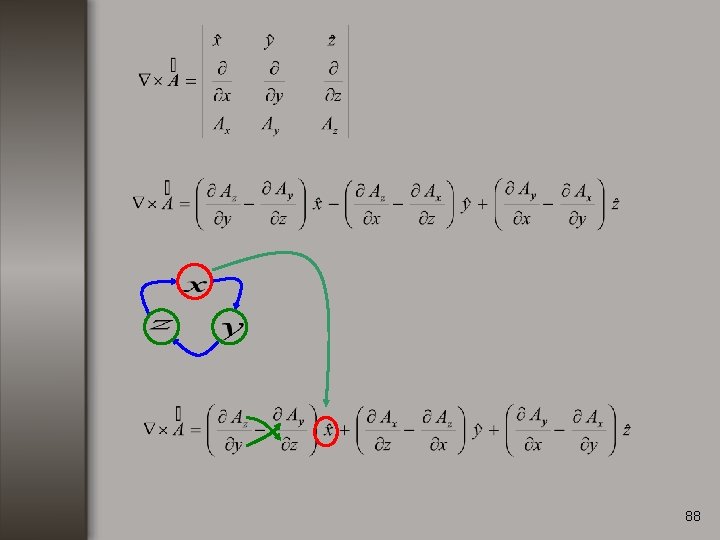
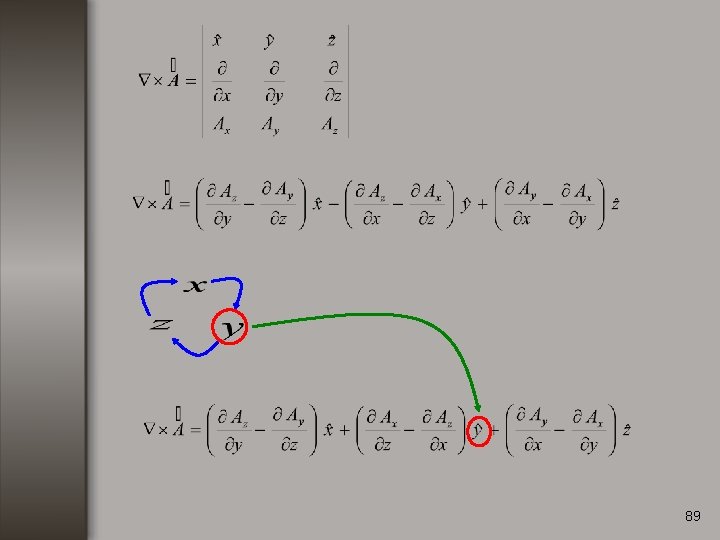
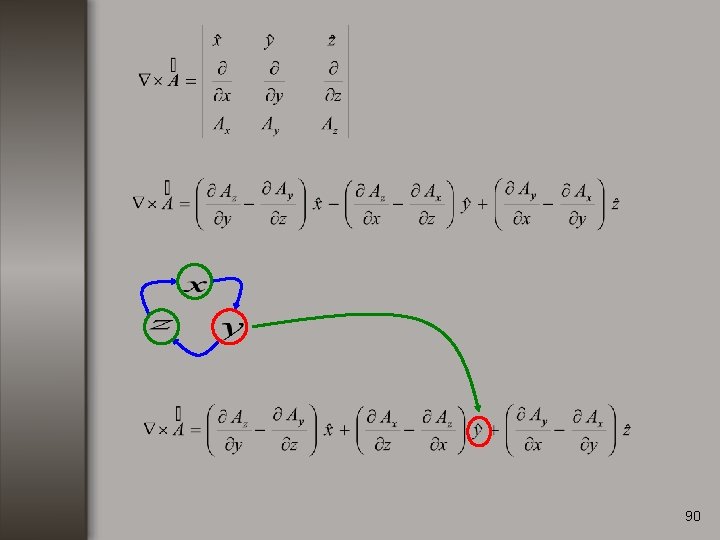
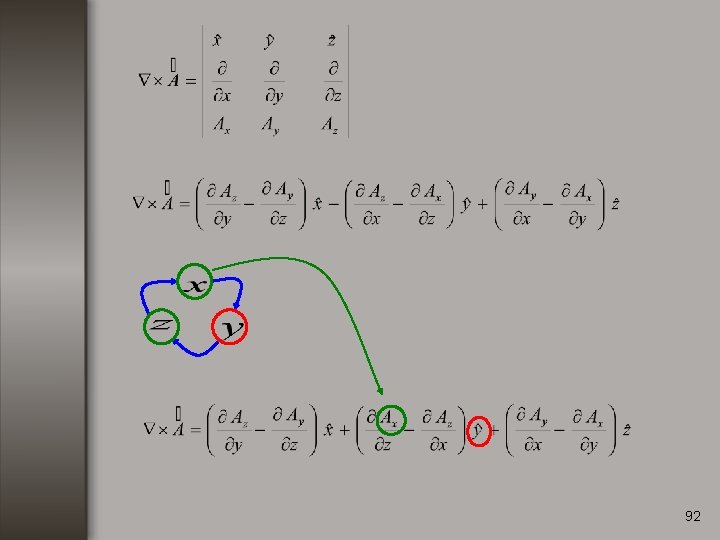
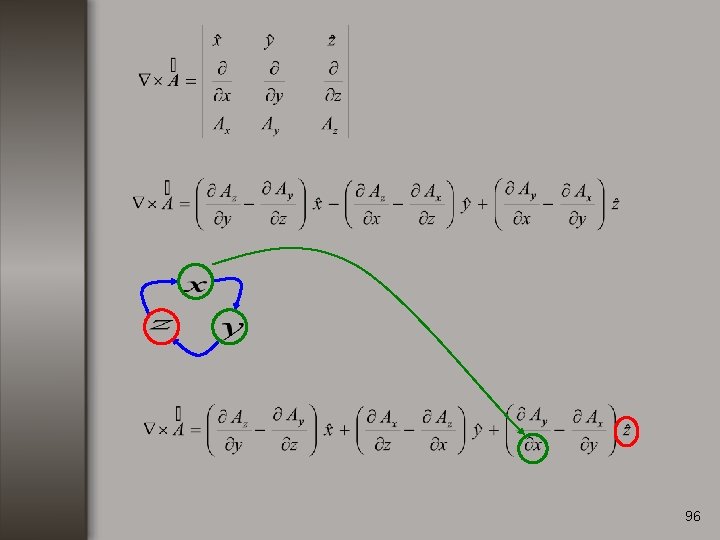
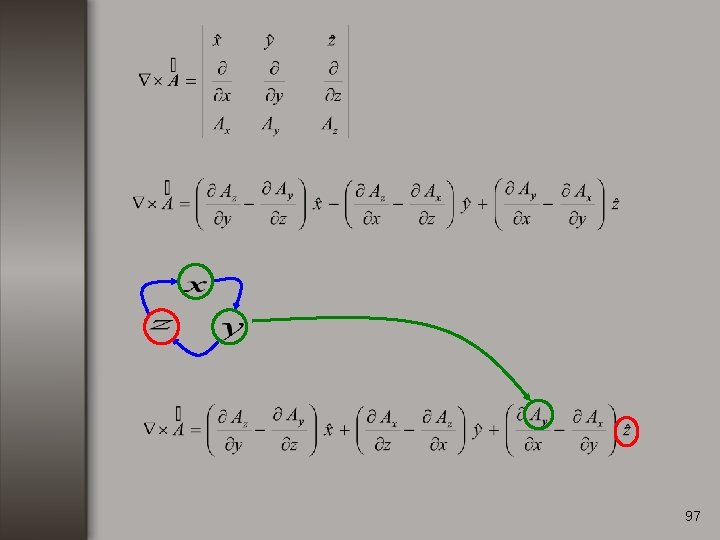
Rotacional. Consideremos una función vectorial de la forma: El rotacional de se define como: 82
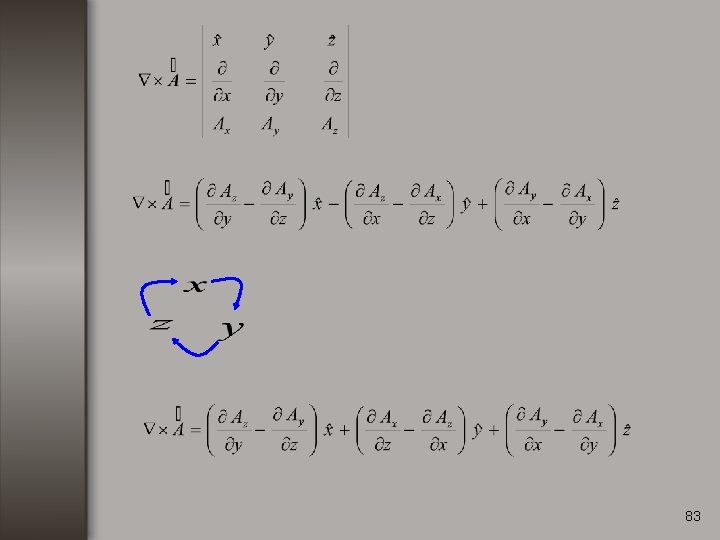
83

84

85

86

87

88

89

90

91

92

93

94

95

96

97
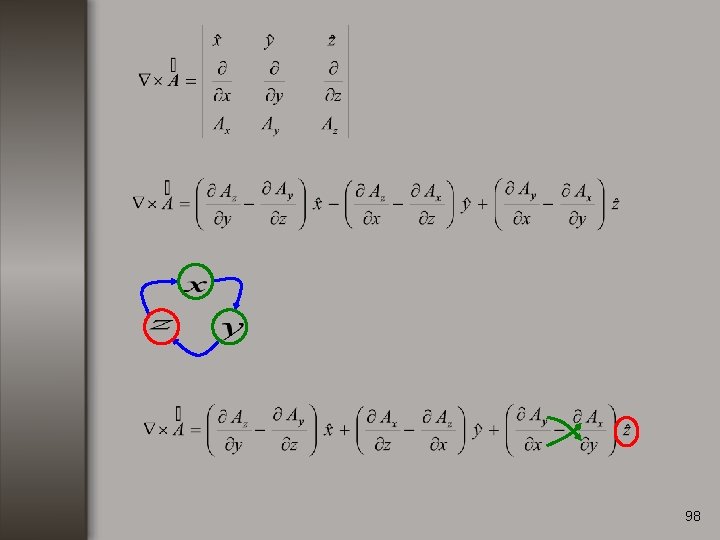
98

99

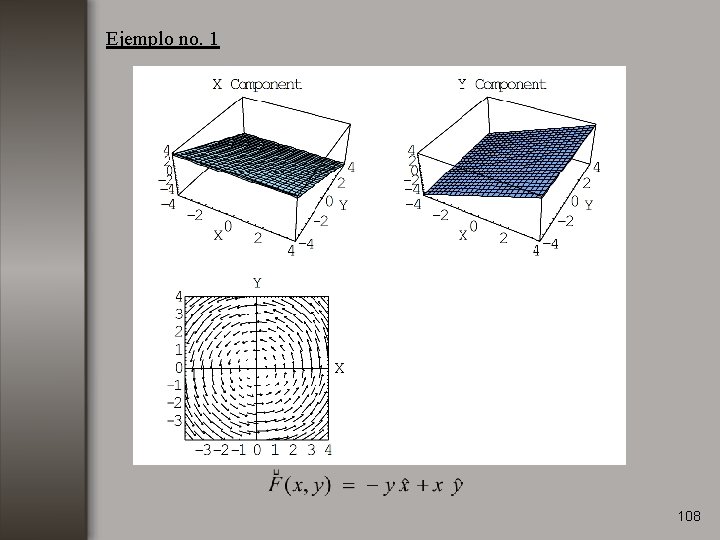
Ejemplo no. 1 Calcular el rotacional de la función: 100

Ejemplo no. 1 Calcular el rotacional de la función: 101

Ejemplo no. 1 Calcular el rotacional de la función: 102

Ejemplo no. 1 Calcular el rotacional de la función: 103

Ejemplo no. 1 Calcular el rotacional de la función: 104

Ejemplo no. 1 Calcular el rotacional de la función: 105

Ejemplo no. 1 Calcular el rotacional de la función: 106

Ejemplo no. 1 Calcular el rotacional de la función: 107

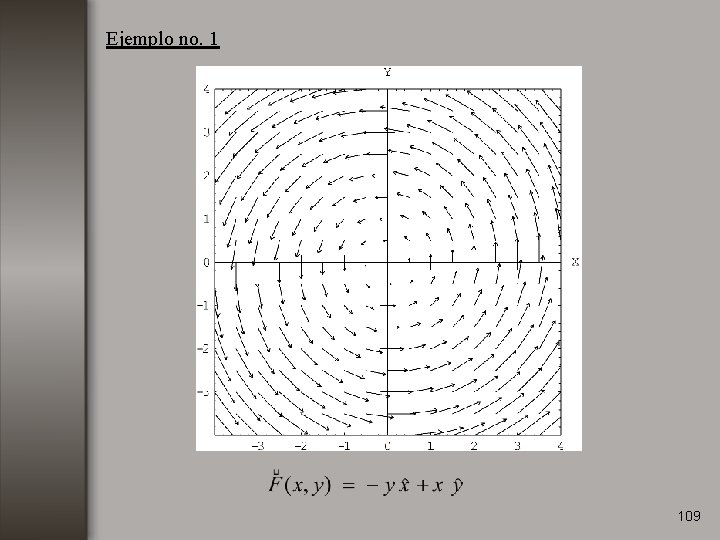
Ejemplo no. 1 108

Ejemplo no. 1 109

Ejemplo no. 2 Calcular el rotacional de la función: 110

Ejemplo no. 2 Calcular el rotacional de la función: 111

Ejemplo no. 2 Calcular el rotacional de la función: 112

Ejemplo no. 2 Calcular el rotacional de la función: 113

Ejemplo no. 2 Calcular el rotacional de la función: 114

Ejemplo no. 2 Calcular el rotacional de la función: 115

Ejemplo no. 2 Calcular el rotacional de la función: 116

Ejemplo no. 2 Calcular el rotacional de la función: 117

Ejemplo no. 2 Calcular el rotacional de la función: 118

Ejemplo no. 2 Calcular el rotacional de la función: 119

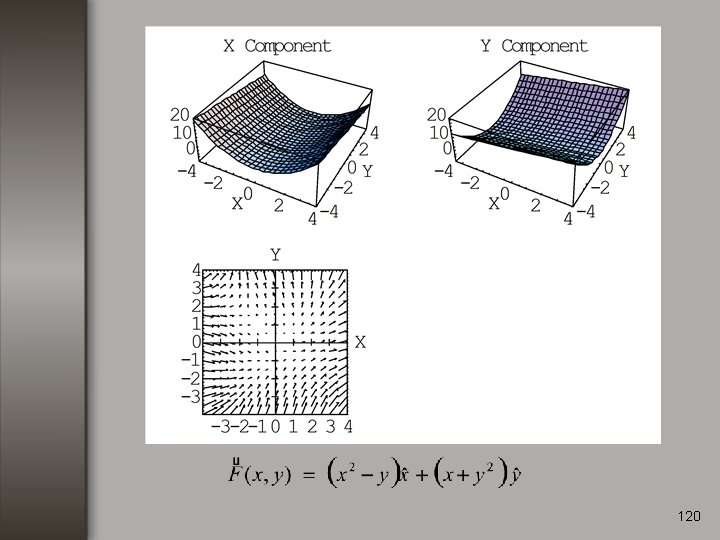
120

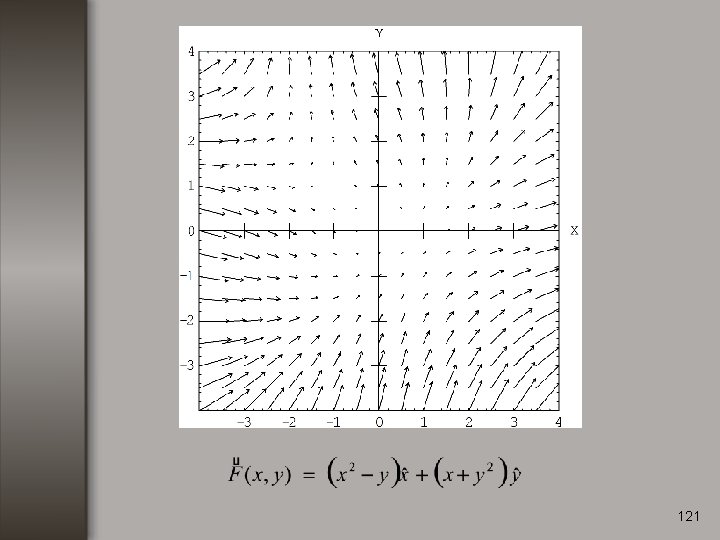
121

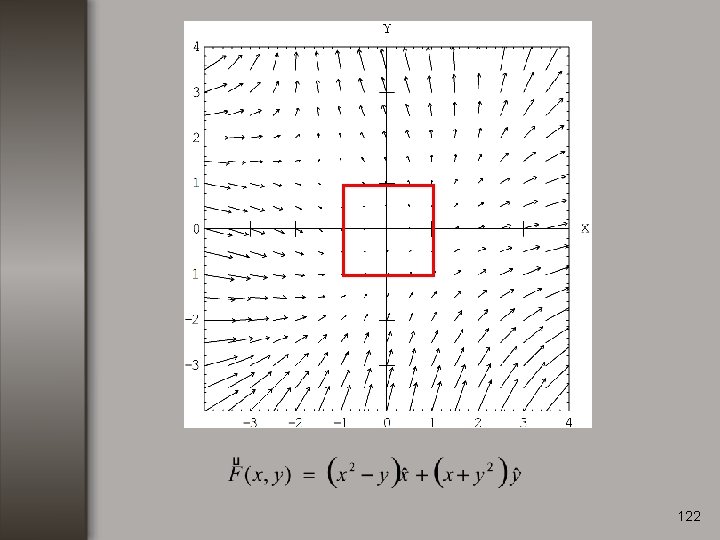
122

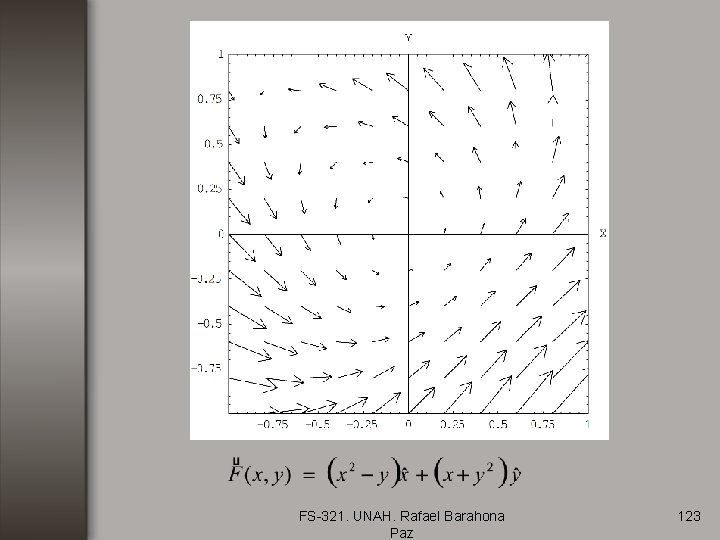
FS-321. UNAH. Rafael Barahona Paz 123

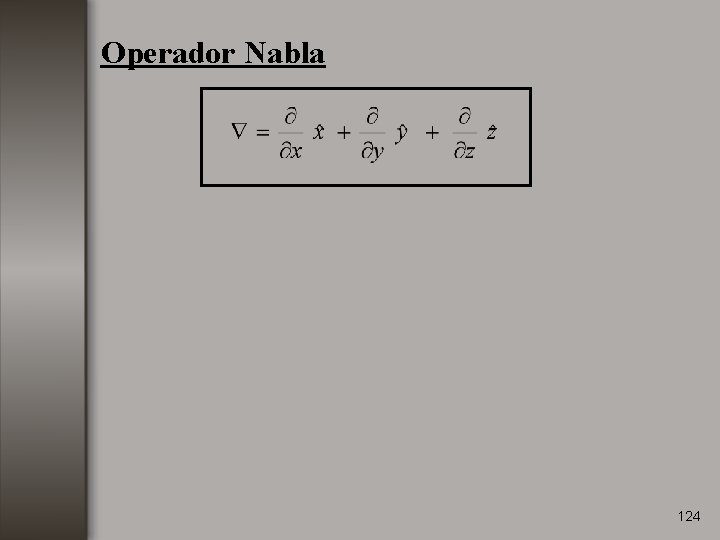
Operador Nabla 124

Operador Nabla Gradiente: 125

Operador Nabla Divergencia: 126

Operador Nabla Rotacional: 127

Laplaciano 128

Laplaciano Cuando actúa sobre una función escalar: 129

Cuando actúa sobre una función vectorial: 130

Propiedades importantes 131