Electric Charge and Coulombs Law Electric Charges the

Electric Charge and Coulomb’s Law

Electric Charges: the basis of electricity is charge. • The charge on an atom is determined by the subatomic particles that make it up. Proton- has a positive charge and is located in the nucleus. Neutron- has no charge (is neutral) and is also located in the nucleus as it fills in the spaces between the protons. Electron- has a negative charge and is located outside of the nucleus in an electron cloud around the atom.

Two types of charge: • Positive Charge: A shortage of electrons. • Negative Charge: An excess of electrons. • Conservation of charge – The net charge of a closed system remains constant.

Fundamental Charge: The charge on one electron. • e = 1. 6 x 10 -19 C • Unit of charge is a Coulomb (C)

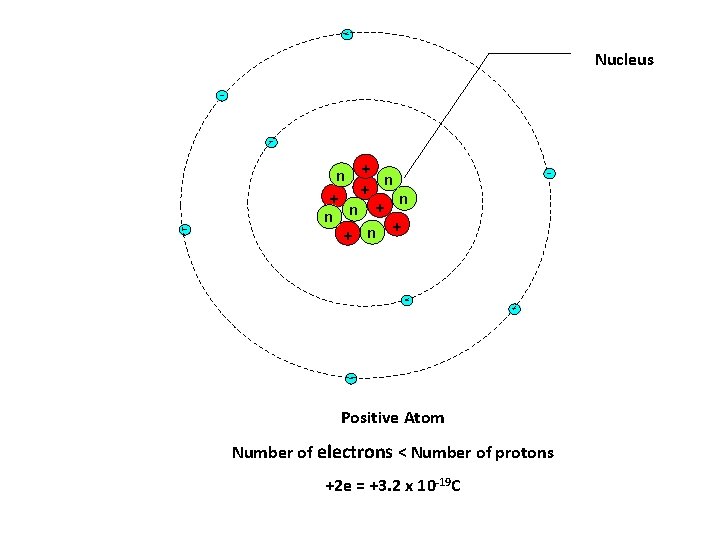
Nucleus - - n + + n - - - Positive Atom Number of electrons < Number of protons +2 e = +3. 2 x 10 -19 C

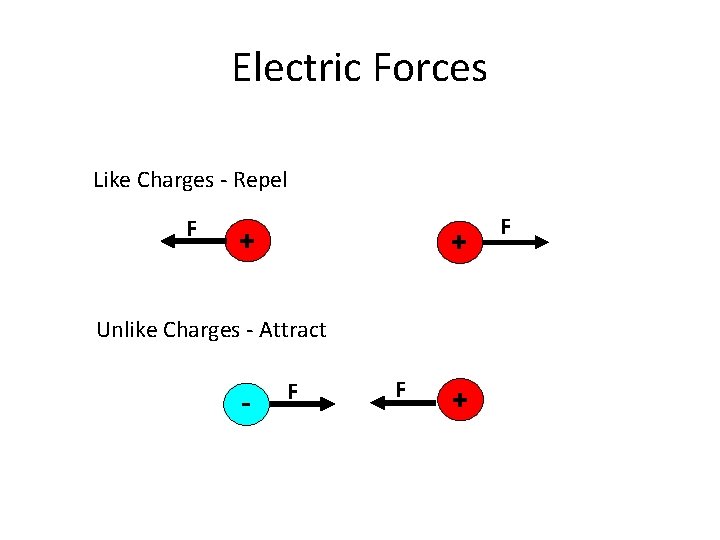
Electric Forces Like Charges - Repel F + + Unlike Charges - Attract - F F + F

Coulomb’s Law • Coulomb’s law states that two stationary point q₁ and q₂ repel or attract each other with a force which • a) is directly proportional to the product q₁ q₂ of magnitude of the charges, • b) is inversely propotional to the square of the distance r between them, • c) acts along the line joining the charges.

Coulomb’s Law – Gives the electric force between two point charges. Inverse Square Law k = Coulomb’s Constant = 9. 0 x 109 Nm 2/C 2 q 1 = charge on mass 1 q 2 = charge on mass 2 r = the distance between the two charges The electric force is much stronger than the gravitational force.

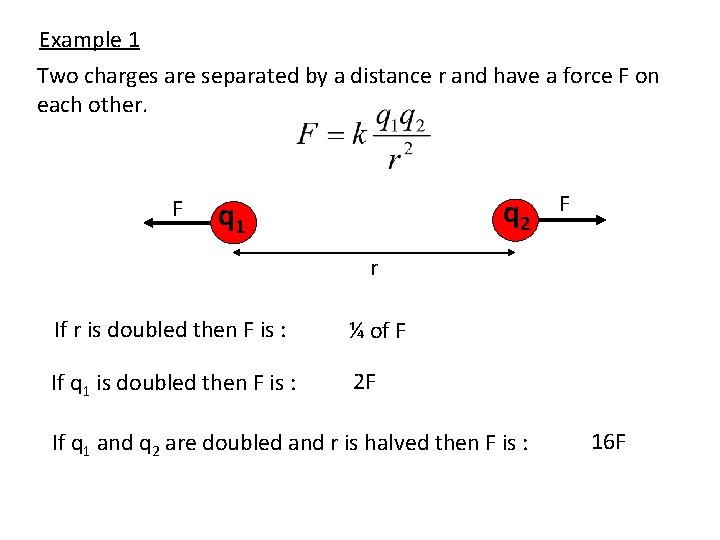
Example 1 Two charges are separated by a distance r and have a force F on each other. F q 2 q 1 F r If r is doubled then F is : ¼ of F If q 1 is doubled then F is : 2 F If q 1 and q 2 are doubled and r is halved then F is : 16 F

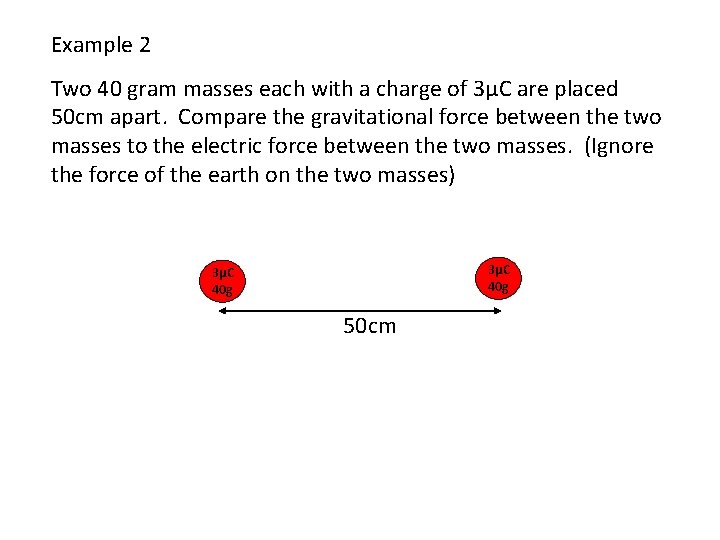
Example 2 Two 40 gram masses each with a charge of 3μC are placed 50 cm apart. Compare the gravitational force between the two masses to the electric force between the two masses. (Ignore the force of the earth on the two masses) 3μC 40 g 50 cm

The electric force is much greater than the gravitational force

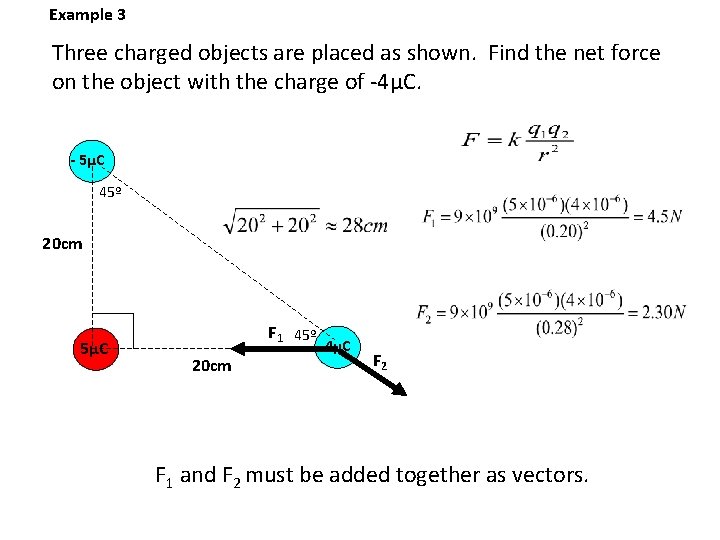
Example 3 Three charged objects are placed as shown. Find the net force on the object with the charge of -4μC. - 5μC 45º 20 cm 5μC F 1 45º 20 cm - 4μC F 2 F 1 and F 2 must be added together as vectors.

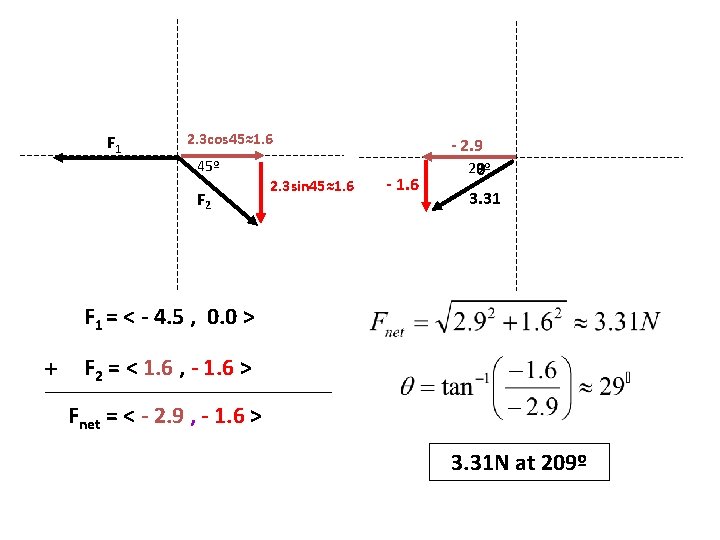
F 1 2. 3 cos 45≈1. 6 45º F 2 2. 3 sin 45≈1. 6 - 2. 9 29º θ 3. 31 F 1 = < - 4. 5 , 0. 0 > + F 2 = < 1. 6 , - 1. 6 > Fnet = < - 2. 9 , - 1. 6 > 3. 31 N at 209º

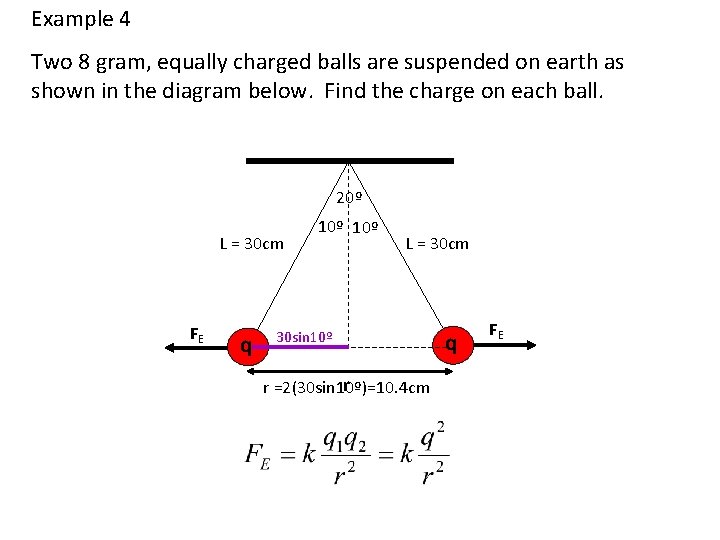
Example 4 Two 8 gram, equally charged balls are suspended on earth as shown in the diagram below. Find the charge on each ball. 20º L = 30 cm FE q 10º L = 30 cm 30 sin 10º r r =2(30 sin 10º)=10. 4 cm q FE

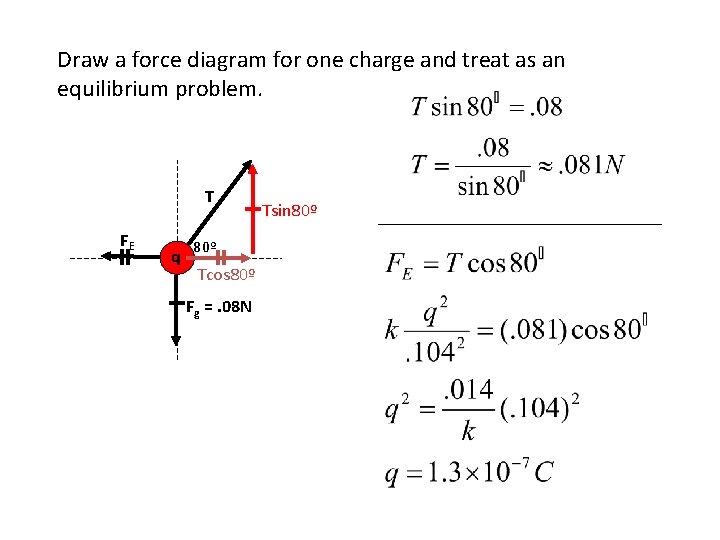
Draw a force diagram for one charge and treat as an equilibrium problem. T FE q 80º Tcos 80º Fg =. 08 N Tsin 80º

ELECTRIC FIELD An electric field is defined as any region in which, an electric test charge, if brought into the vicinity, would experience an electric force. Electric field is a vector field.

The intensity (or field strength) E at any point is defined as the force per unit positive test charge placed at that point. Mathematically E=F/q₀ where F is the force exerted on small test charge q₀