Vectors Representing Vectors Vector a quantity that has

Vectors

Representing Vectors • Vector- a quantity that has both magnitude and direction • Graphical Representation: Direction Magnitude

Magnitude to Scale • Scale: 1 cm = 10 m/s The vector measures to be 14 cm long. Therefore the magnitude of the vector is 140 m/s

Magnitude to Scale • Conversely, if we are told that a vector has a magnitude of 75 m/s. Drawing the vector to scale, we would draw an arrow 7. 5 cm long. 7. 5 cm

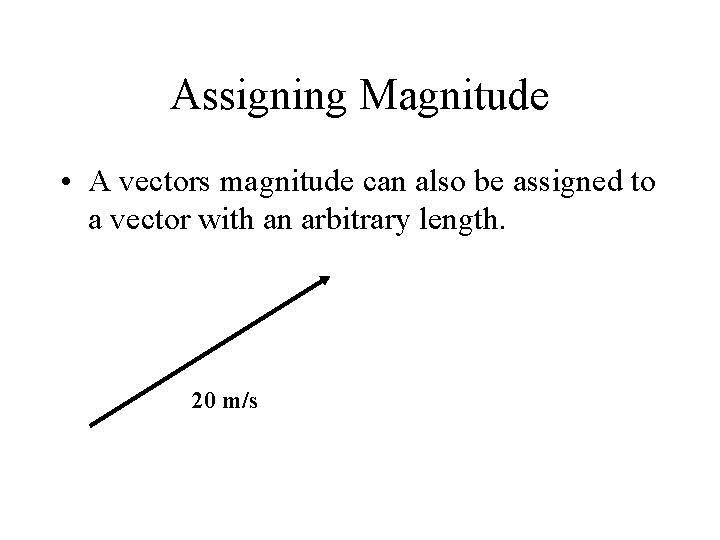
Assigning Magnitude • A vectors magnitude can also be assigned to a vector with an arbitrary length. 20 m/s

Direction • The direction of vectors along the x or y axis can be denoted by + or -. • Vectors at an angle can be denoted by an angle measurement relative to the axis: 25° above the x-axis 70° below the x-axis or 250°

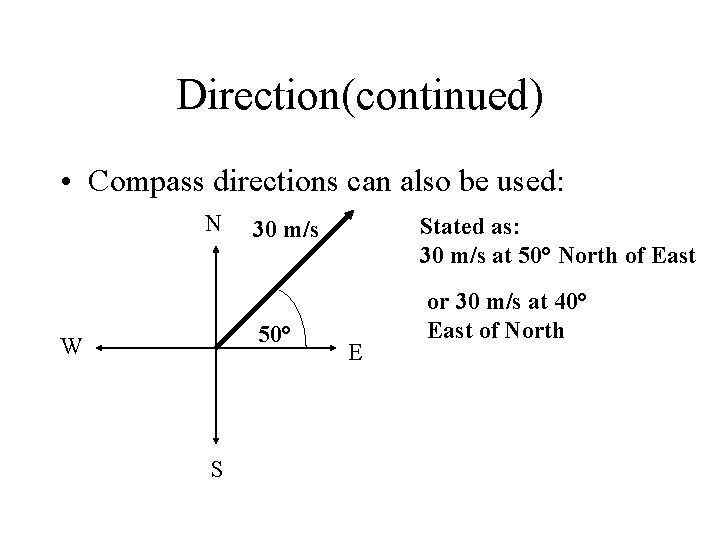
Direction(continued) • Compass directions can also be used: N 50° W S Stated as: 30 m/s at 50° North of East 30 m/s E or 30 m/s at 40° East of North

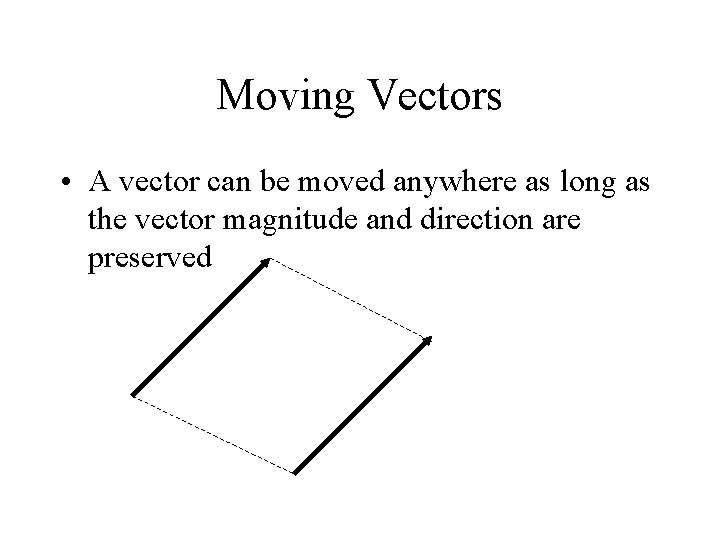
Moving Vectors • A vector can be moved anywhere as long as the vector magnitude and direction are preserved

Vector Operations: Addition • When vectors are added together they produce a new vector that represents the sum of the vectors. We call this new vector the resultant.

Adding Parallel Vectors • Adding vectors A and B A = 10 m/s B = 5 m/s • When adding vectors arrange them in headto-tail orientation A+B Resultant = 15 m/s

Commutative Property • Vector Addition is commutative. Two vectors can be added in any order. • A+B=B+A A+B B+A

Adding Vectors at an Angle • Add vectors A and B A = 10 m/s B = 5 m/s • Again arrange vectors in head-to-tail A orientation B

Adding Vectors at an Angle (continued) • The resultant is then drawn from the tail of the first vector to the head of the last vector. A = 10 m/s R B = 5 m/s • Solve by Pythagorean Theorem

Adding Vectors at an Angle (continued) • The angle can then be found using right triangle trigonometry A = 10 m/s R = 11. 2 m/s B = 5 m/s

Adding Vectors at Acute and Obtuse Angles • Add vectors A and B A = 10 m/s B = 5 m/s 30° • Again arrange vectors in head-to-tail A orientation B

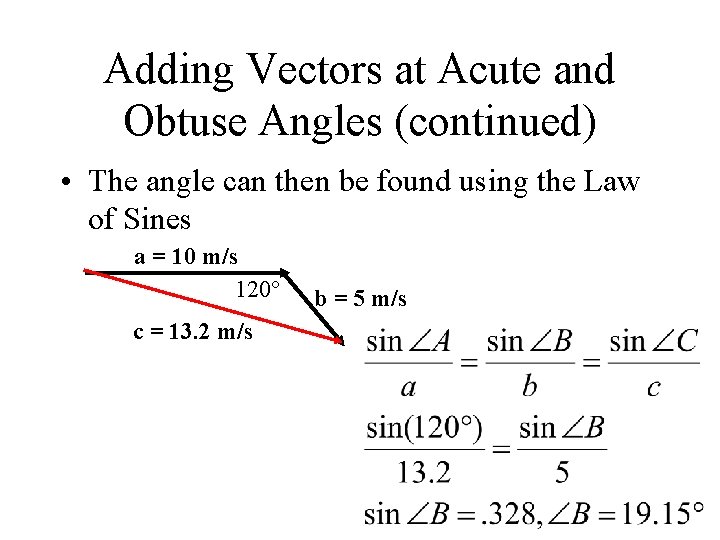
Adding Vectors at Acute and Obtuse Angles (continued) • Draw in the resultant A = 10 m/s 120° Determine angle by adding together 90 and 30. B = 5 m/s C • Solve by Law of Cosines

Adding Vectors at Acute and Obtuse Angles (continued) • The angle can then be found using the Law of Sines a = 10 m/s 120° c = 13. 2 m/s b = 5 m/s

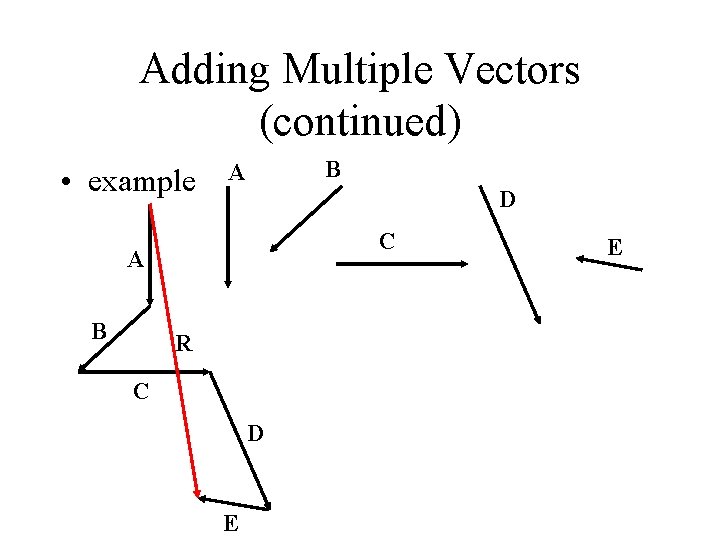
Adding Multiple Vectors • Vector Addition is associative. Three vectors can be added in any order. • (a + b) + c = a + (b + c) • Therefore multiple vectors can be added in any order and you will receive the same resultant.

Adding Multiple Vectors (continued) • example B A D C A B R C D E E

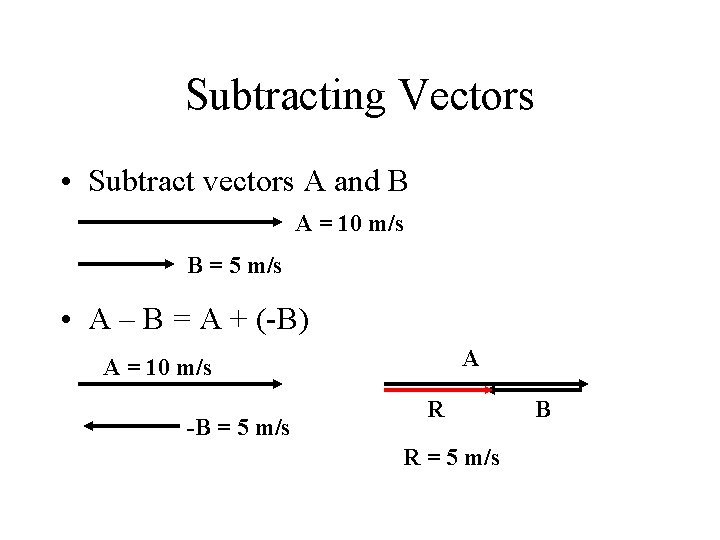
Subtracting Vectors • Subtract vectors A and B A = 10 m/s B = 5 m/s • A – B = A + (-B) A A = 10 m/s -B = 5 m/s R R = 5 m/s B

Components of Vectors • For convenience we would like to classify a vector’s direction as pointing in either the x or y directions. • However, this is not obvious for vectors that do not lie along the x or y-axis. • This is why we have a need to describe how much of the vector is projected in the x and y directions. • This is done through the use of components

Components of Vectors (continued) • Given the following vector, determine its components in x and y. v =20 m/s 35° • First, align the vector on a coordinate axis.

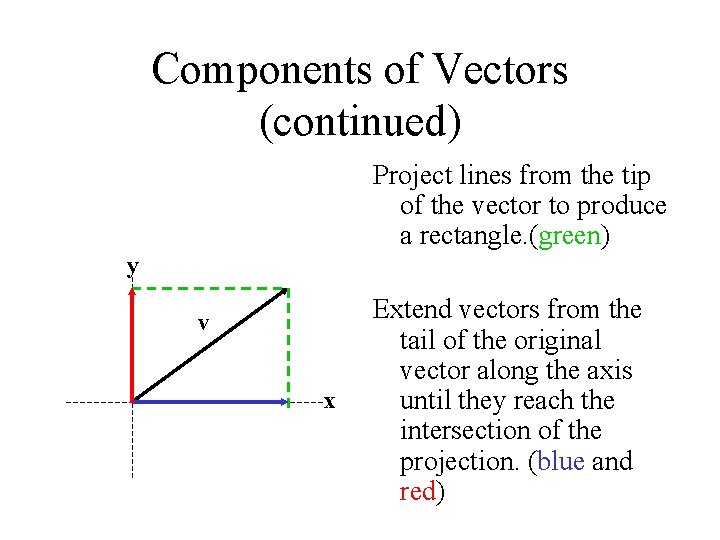
Components of Vectors (continued) Project lines from the tip of the vector to produce a rectangle. (green) y v x Extend vectors from the tail of the original vector along the axis until they reach the intersection of the projection. (blue and red)

Components of Vectors (continued) • Each new vector is a vector in either x or y or an x or y component. The components can then be solved for by using right triangle trigonometry. y vy s / m 0 =2 v 35° vx x