C 2 MAGNITUDES FSICAS Magnitudes fsicas escalares y












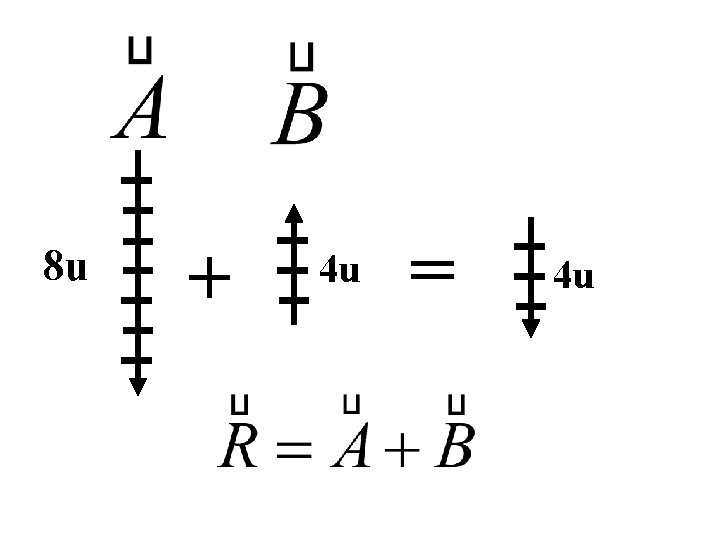







- Slides: 42

C 2 MAGNITUDES FÍSICAS. • Magnitudes físicas escalares y vectoriales. Algebra vectorial. • Ejemplos Bibliog. Sears, Física universitaria 1999, Hewitt, Física conceptual 1999

Magnitudes físicas por su naturaleza Escalares Vectoriales

Magnitudes físicas Escalares Asociadas a propiedades que pueden ser caracterizadas a través de una cantidad Vectoriales Asociadas a propiedades que se caracterizan no sólo por su cantidad sino por su dirección y su sentido

Escalares Magnitudes físicas Masa, densidad, temperatura, energía, trabajo, etc Vectoriales Velocidad, fuerza, cantidad de movimiento, aceleración, torque, etc.

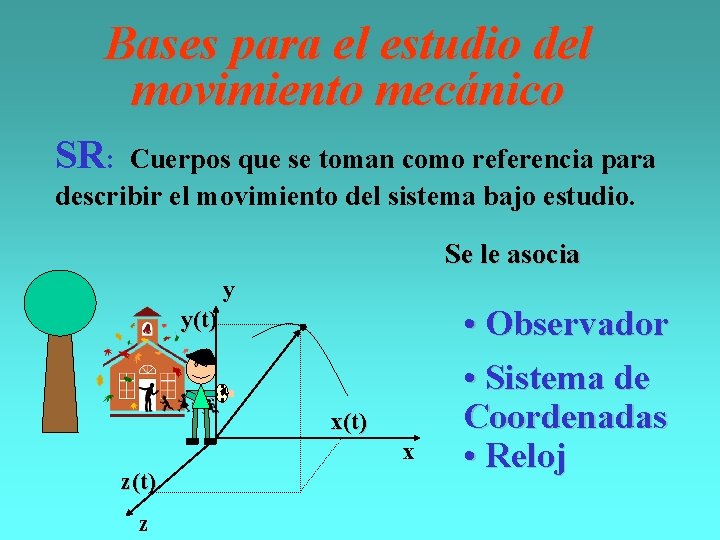
Bases para el estudio del movimiento mecánico SR: Cuerpos que se toman como referencia para describir el movimiento del sistema bajo estudio. Se le asocia y y(t) x z(t) z • Observador • Sistema de Coordenadas • Reloj

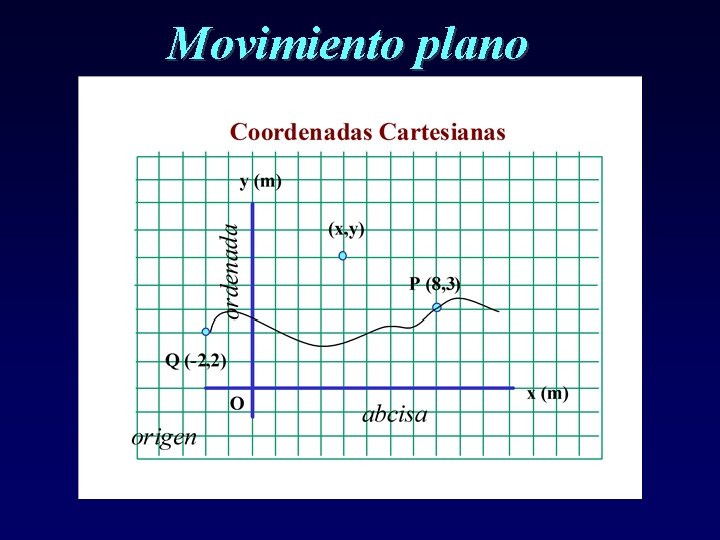
Movimiento plano

Movimiento plano


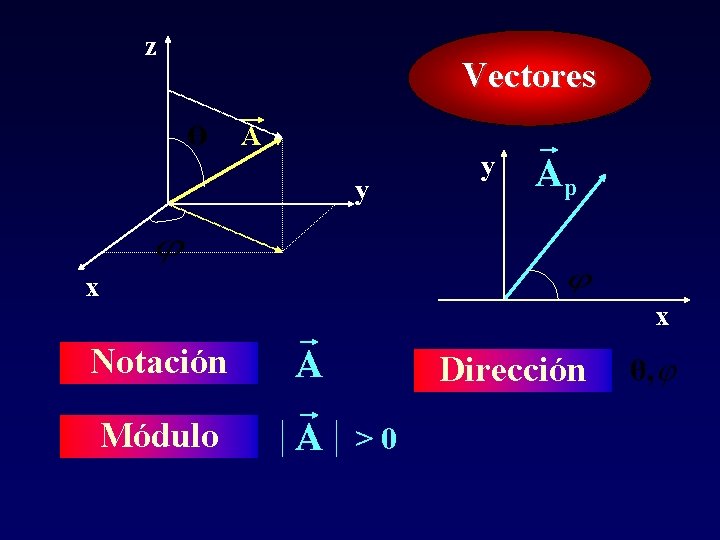
z Vectores A y y Ap x x Notación A Módulo A Dirección >0

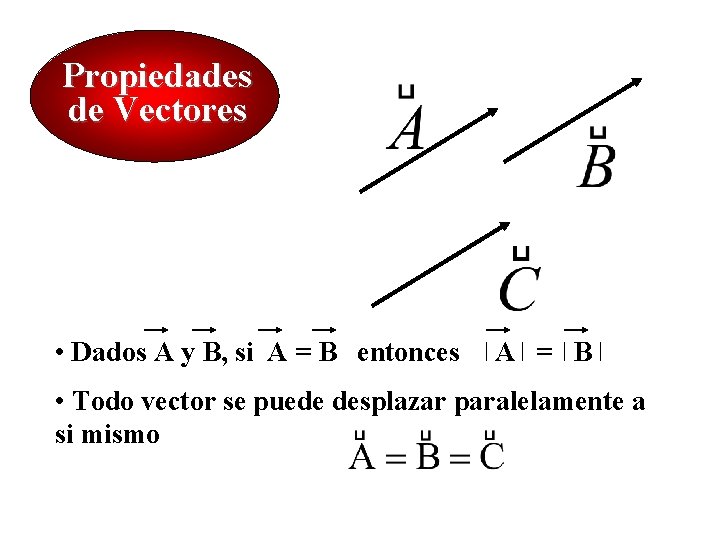
Propiedades de Vectores • Dados A y B, si A = B entonces A = B • Todo vector se puede desplazar paralelamente a si mismo

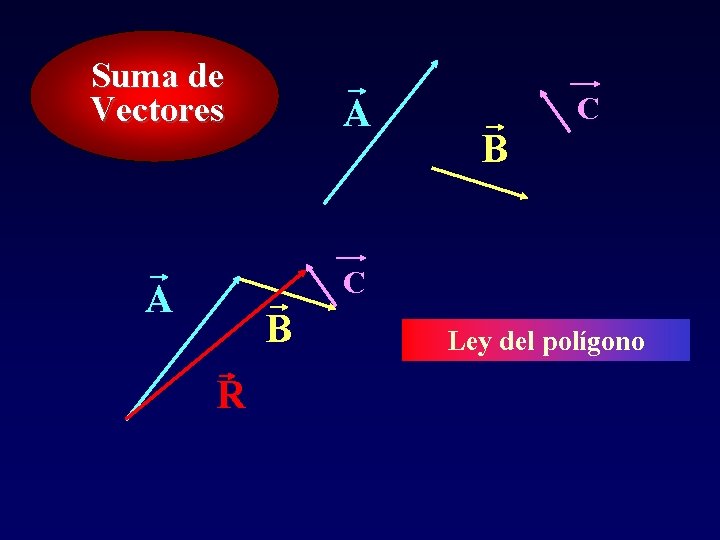
Suma de Vectores A C B C A B R Ley del polígono

El vector resultante es aquel que vector que va desde el origen del primer vector hasta el extremo del ultimo

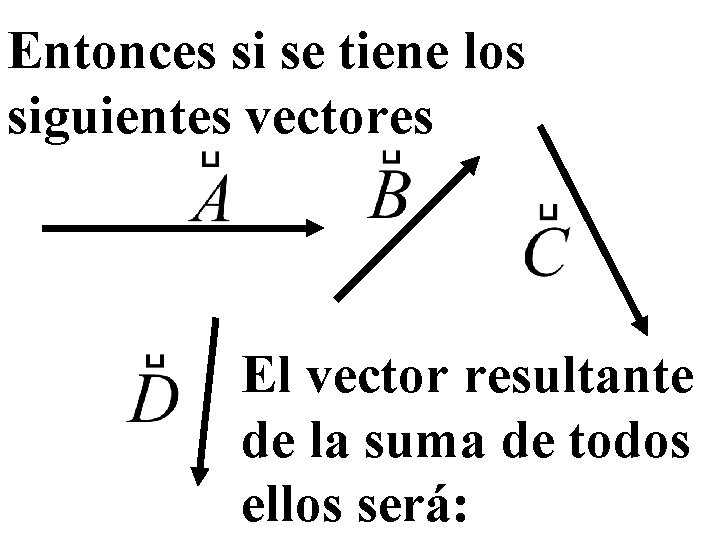
Entonces si se tiene los siguientes vectores El vector resultante de la suma de todos ellos será:


Propiedades de Vectores Opuesto Nulo Vector unitario A -A 0 = A + ( -A )

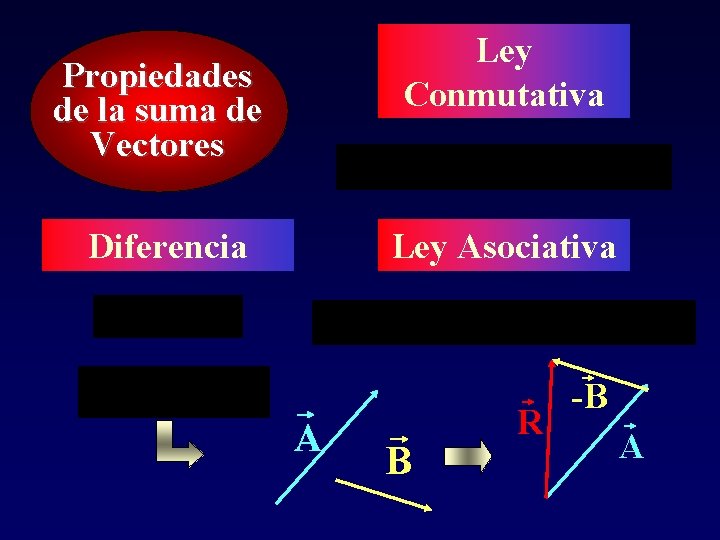
Ley Conmutativa Propiedades de la suma de Vectores Ley Asociativa Diferencia A B R -B A

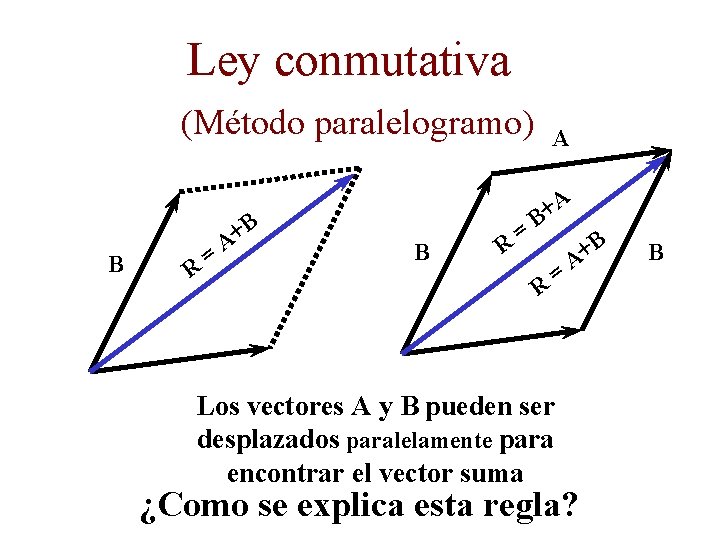
Ley conmutativa (Método paralelogramo) B R = B + A B R = A A + B R Los vectores A y B pueden ser desplazados paralelamente para encontrar el vector suma = B + A ¿Como se explica esta regla? B

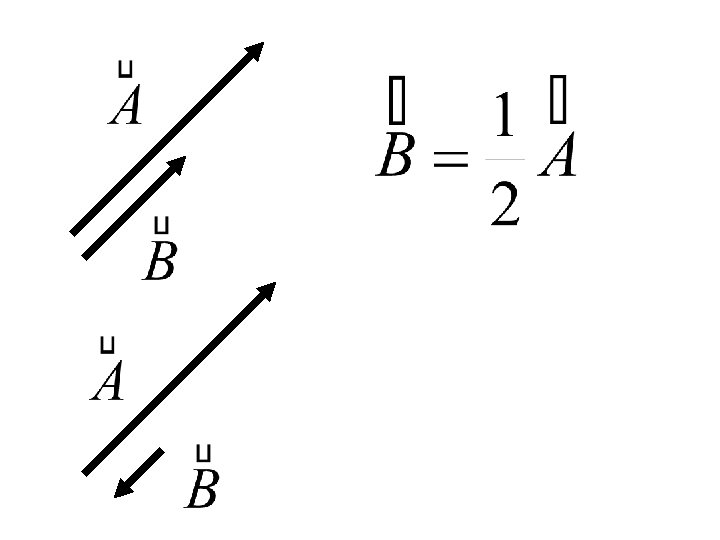
Multiplicación de un vector por un escalar Dado dos vectores Se dicen que son paralelos si


Ejemplo 8: Hallar el vector resultante de la suma de los siguientes vectores A B C A B R = 2 C

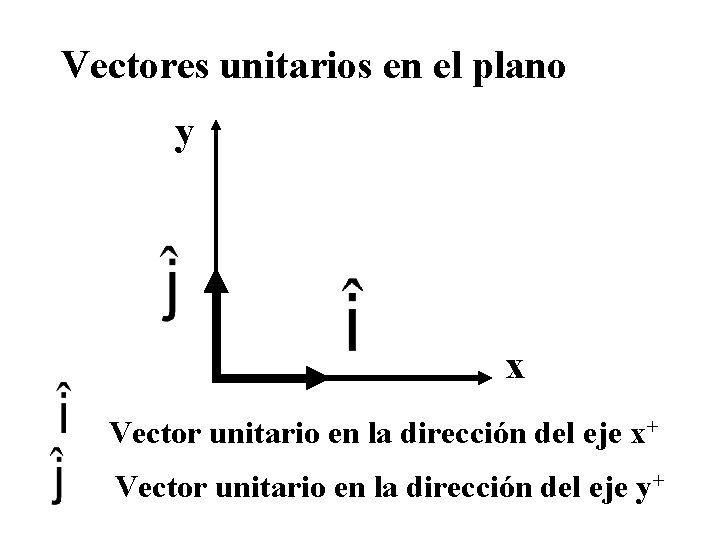
Vectores unitarios en el plano y x Vector unitario en la dirección del eje x+ Vector unitario en la dirección del eje y+

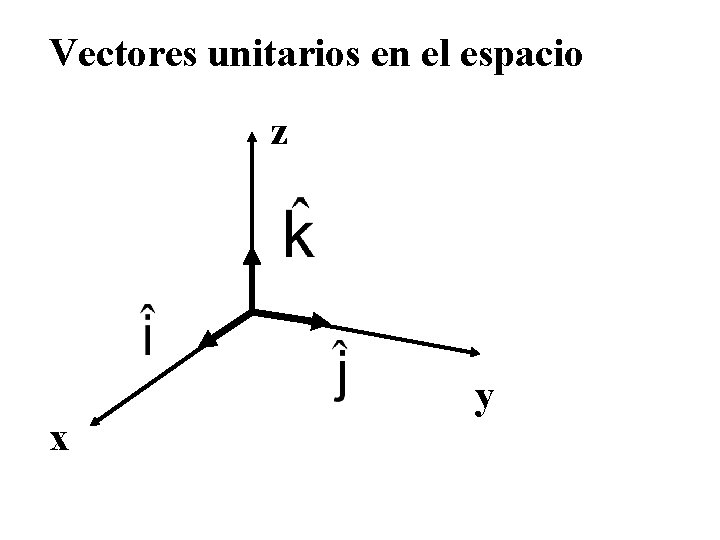
Vectores unitarios en el espacio z x y

z Representación de un vector Az A Ay y Ax x

Observaciones: Las componentes rectangulares de un vector dependen del sistema coordenado elegido. La magnitud del vector no cambia. Permanece invariante en cualquier sistema coordenado

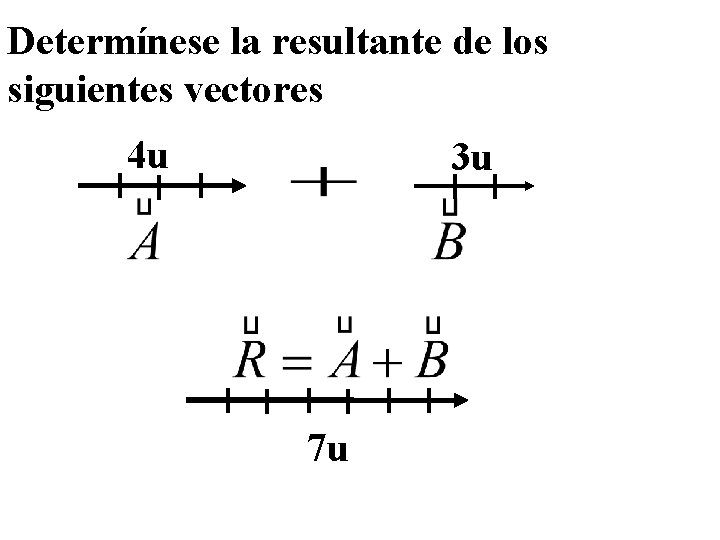
Determínese la resultante de los siguientes vectores 4 u 3 u 7 u
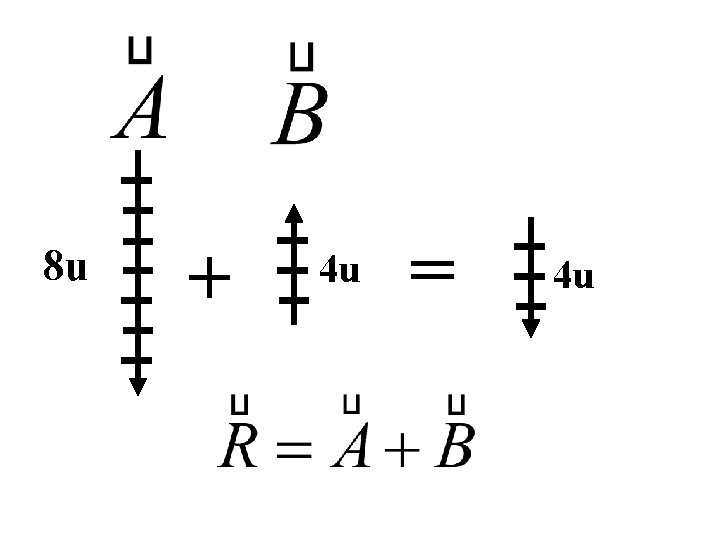
8 u + 4 u = 4 u

Observamos que, cuando los vectores están en la misma dirección podemos determinar fácilmente su magnitud ¿Que sucede si los vectores no están en la misma dirección ? , ¿ podremos determinar directamente su magnitud ?

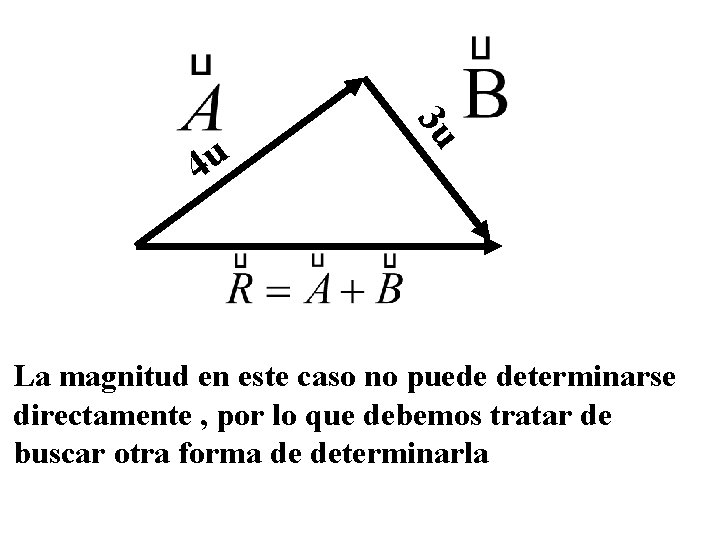
3 u 4 u La magnitud en este caso no puede determinarse directamente , por lo que debemos tratar de buscar otra forma de determinarla

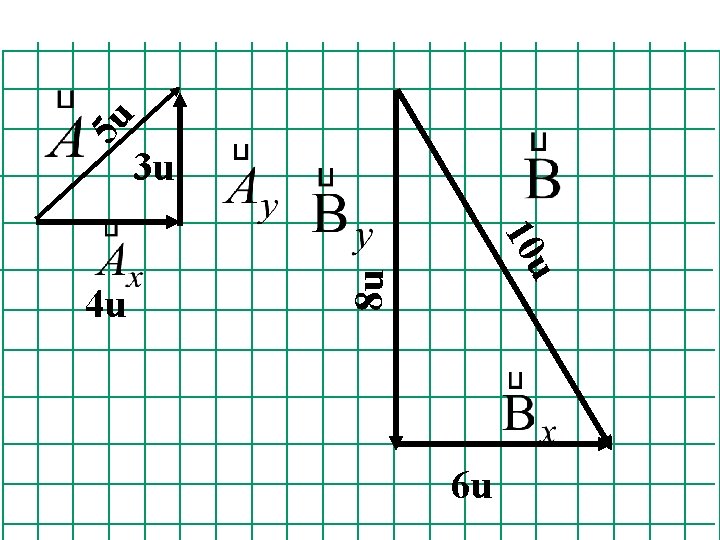
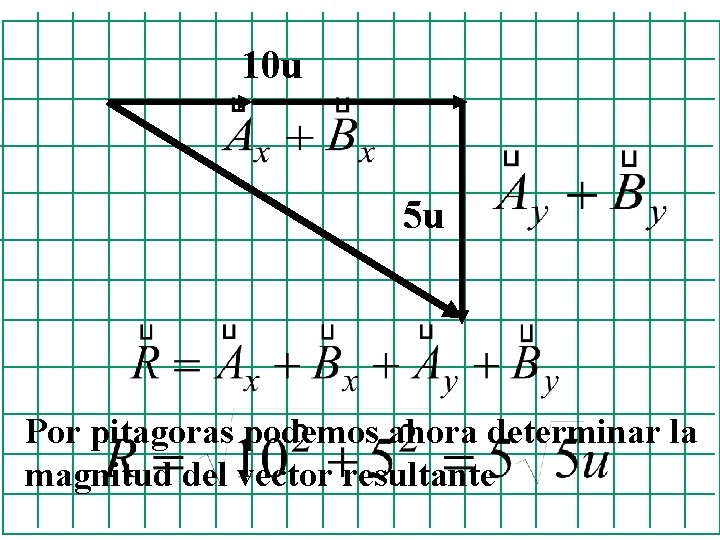
5 u 3 u 8 u u 10 4 u 6 u

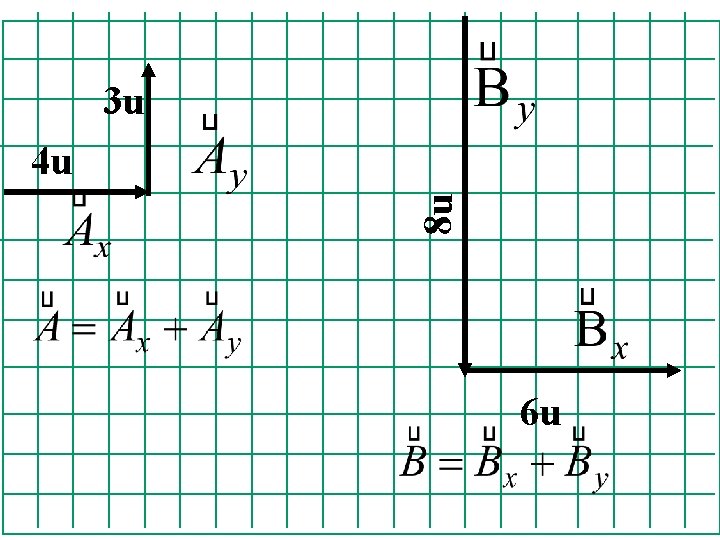
3 u 8 u 4 u 6 u

10 u 5 u Por pitagoras podemos ahora determinar la magnitud del vector resultante


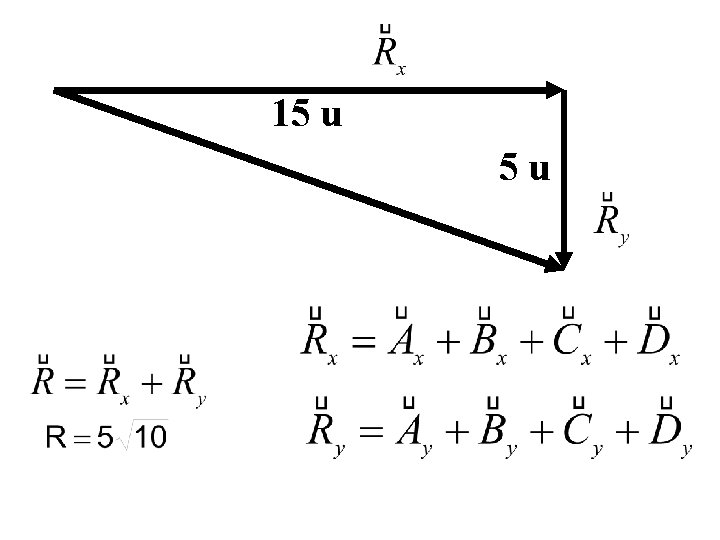
15 u 5 u

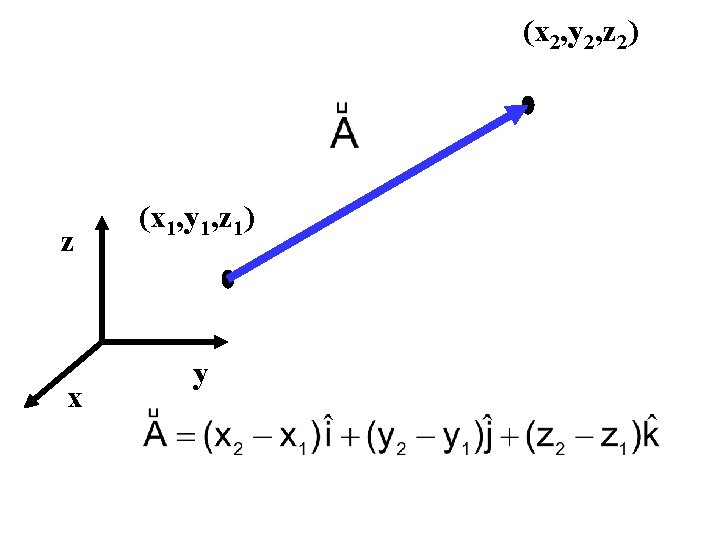
(x 2, y 2, z 2) z x (x 1, y 1, z 1) y Dados los puntos indicados el vector que los une esta representado por

(x 2, y 2, z 2) z x (x 1, y 1, z 1) y

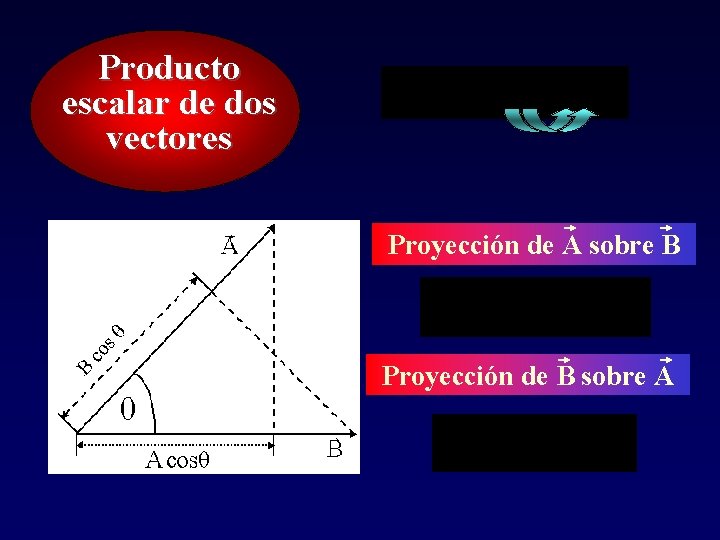
Producto escalar de dos vectores Proyección de A sobre B Proyección de B sobre A


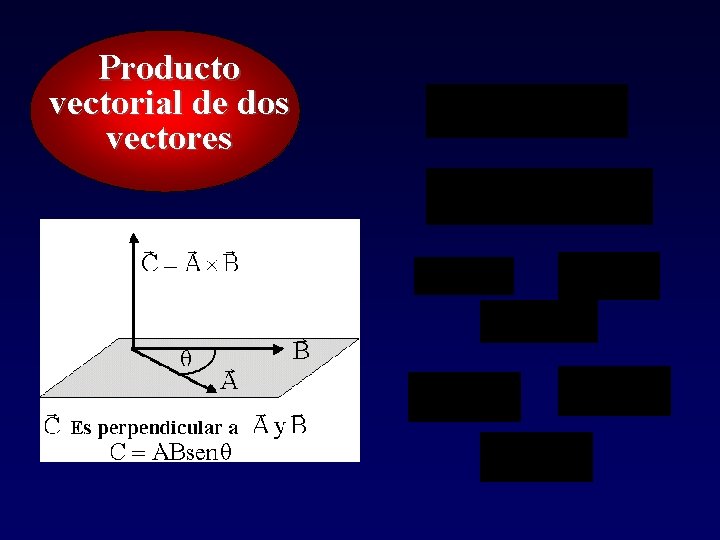
Producto vectorial de dos vectores

Demostrar:

Ejemplo 1: Determinese la suma de los siguientes vectores:

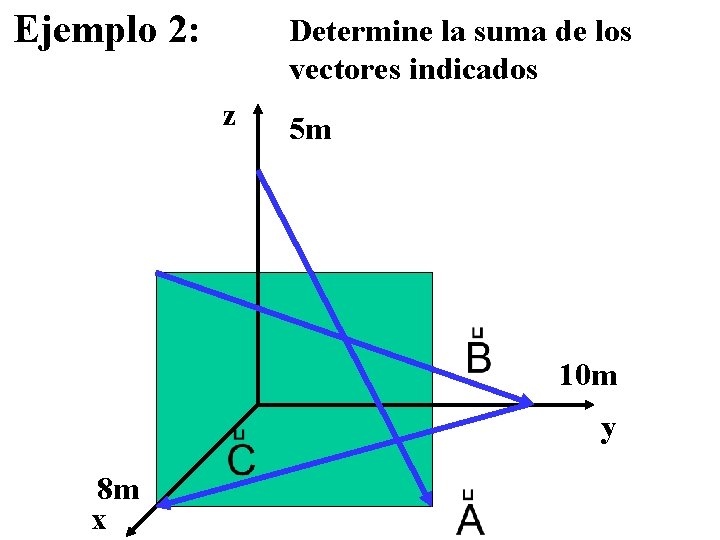
Ejemplo 2: Determine la suma de los vectores indicados z 5 m 10 m y 8 m x

Ejemplo 9 Dados los vectores: Determine : a) El producto escalar entre ellos. b)el producto vectorial entre ambos e) el ángulo que forman entre sí. Tarea 9 c, 9 d y 10
 Cinco magnitudes escalares
Cinco magnitudes escalares Magnitudes vectoriales
Magnitudes vectoriales Magnitudes escalares
Magnitudes escalares Que es una magnitud
Que es una magnitud 30 lb hacia el sur
30 lb hacia el sur Grandezas escalares
Grandezas escalares Grandeza vetorial e escalar
Grandeza vetorial e escalar Escalares
Escalares Physical magnitudes
Physical magnitudes Magnitudes
Magnitudes Sistema internacional de unidades objetivo
Sistema internacional de unidades objetivo Poder de penetración
Poder de penetración A helicopter is traveling at 40m /s
A helicopter is traveling at 40m /s Magnitudes macroeconomicas
Magnitudes macroeconomicas Magnitudes basicas y derivadas
Magnitudes basicas y derivadas Es todo aquello que se puede medir
Es todo aquello que se puede medir Necesitan de un valor numérico y una unidad de medida
Necesitan de un valor numérico y una unidad de medida Si 8 secretarias tardan 3 dias
Si 8 secretarias tardan 3 dias Magnitud tiempo
Magnitud tiempo Magnitudes angulares
Magnitudes angulares Formula de la constante de proporcionalidad
Formula de la constante de proporcionalidad Centi mili micro nano
Centi mili micro nano Monocrómatas
Monocrómatas Utm a kg
Utm a kg Magnitud termodinámica
Magnitud termodinámica Aceleración centrípeta
Aceleración centrípeta La ley de ohm liga tres magnitudes fundamentales que son
La ley de ohm liga tres magnitudes fundamentales que son Ejemplos de magnitudes físicas
Ejemplos de magnitudes físicas Que es la ciencia
Que es la ciencia Cuando es inversamente proporcional
Cuando es inversamente proporcional Proporciones
Proporciones La velocidad
La velocidad Mapa conceptual de sistema de unidades
Mapa conceptual de sistema de unidades Magnitudes derivadas
Magnitudes derivadas Magnitudes físicas fundamentales
Magnitudes físicas fundamentales Conversó de unidades
Conversó de unidades Magnitudes vectoriales
Magnitudes vectoriales Magnitudes correlacionadas ejemplos resueltos
Magnitudes correlacionadas ejemplos resueltos Ganancia transistor
Ganancia transistor