Fsica I Dr Rogerio Enrquez Caldera Graficas Dr







![Los vectores son segmentos de recta dirigidos en [el plano o] el espacio representados Los vectores son segmentos de recta dirigidos en [el plano o] el espacio representados](https://slidetodoc.com/presentation_image_h/252b0bbe94b74aa2bdf05e7466e5e313/image-12.jpg)









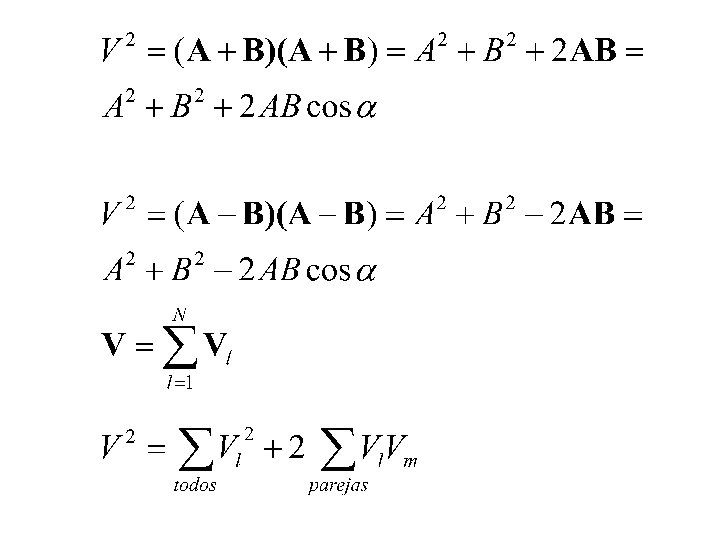



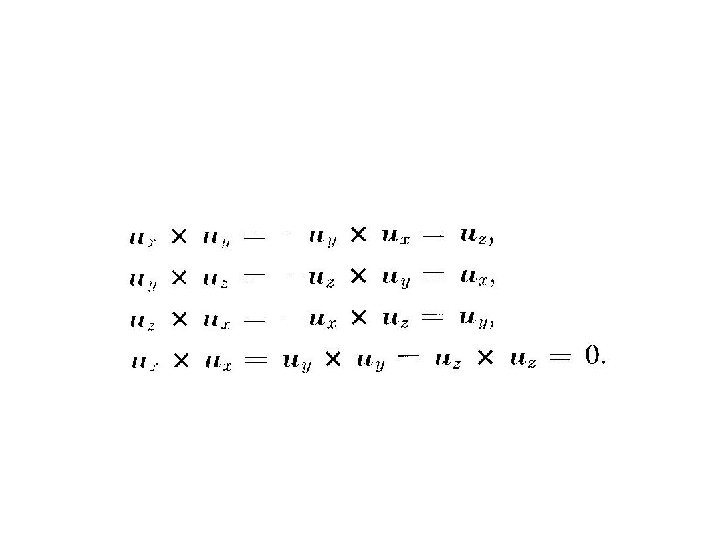
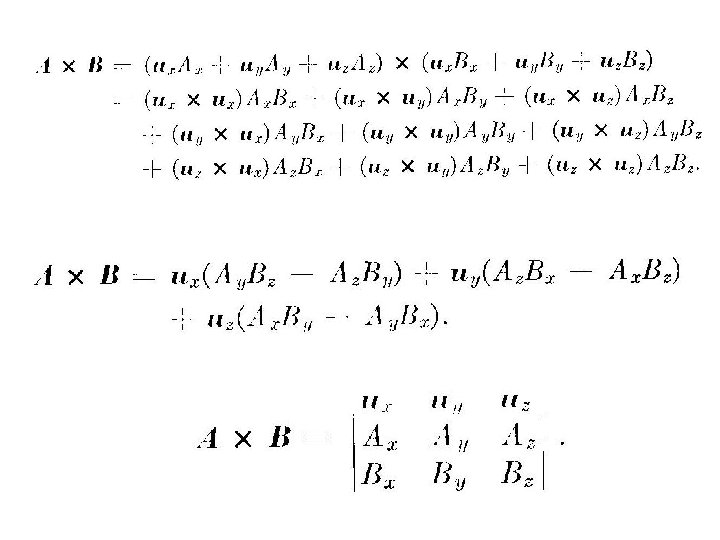
- Slides: 59

Física I Dr. Rogerio Enríquez Caldera (Graficas: Dr. Gustavo Rodríquez)

Vectores • • Definiciones Operaciones Básicas Componentes Vectores en 2 D y 3 D Magnitud Unidades Marcos de referencia

Notación • Se empleará la siguiente notación: – La recta de los números reales es denotada por ℝ – El conjunto de los pares ordenados (x, y) es denotado por ℝ² – El conjunto de las ternas ordenadas (x, y, z) es denotado por ℝ³

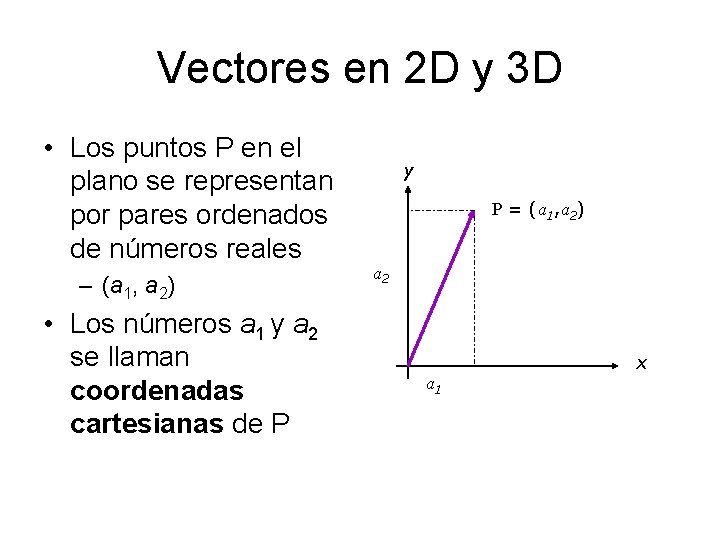
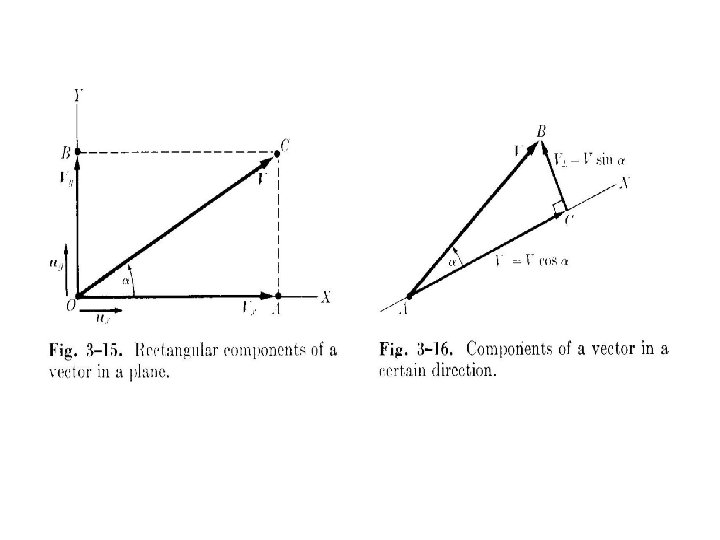
Vectores en 2 D y 3 D • Los puntos P en el plano se representan por pares ordenados de números reales – (a 1, a 2) • Los números a 1 y a 2 se llaman coordenadas cartesianas de P y P = (a 1, a 2) a 2 x a 1

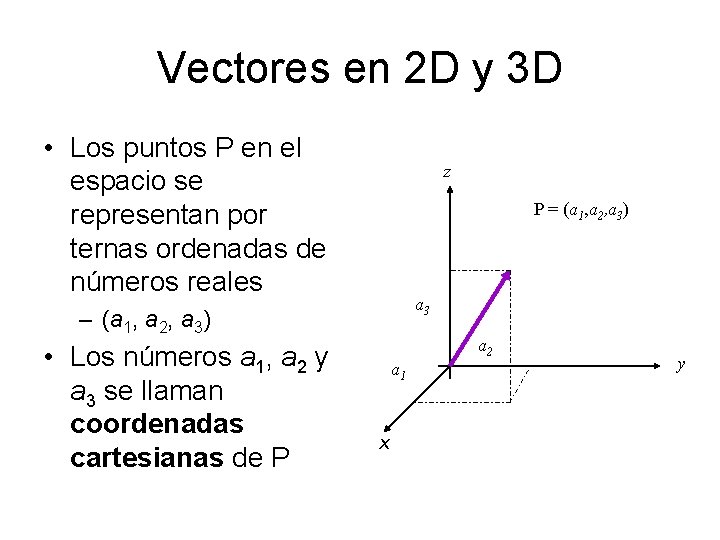
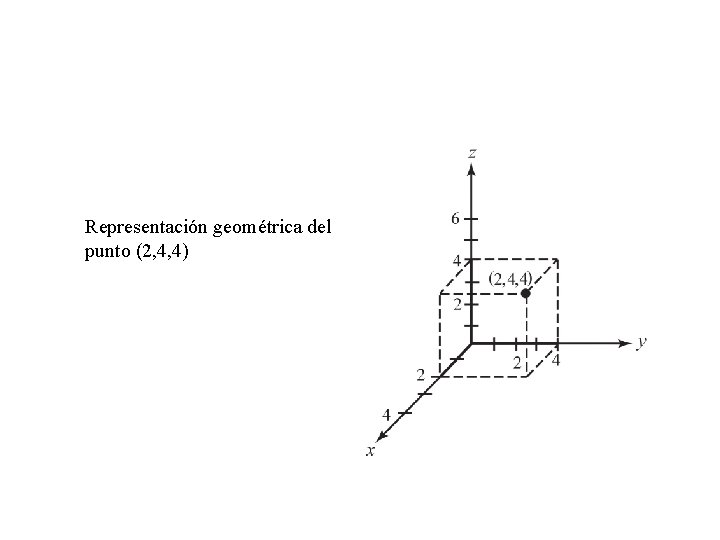
Vectores en 2 D y 3 D • Los puntos P en el espacio se representan por ternas ordenadas de números reales z P = (a 1, a 2, a 3) a 3 – (a 1, a 2, a 3) • Los números a 1, a 2 y a 3 se llaman coordenadas cartesianas de P a 2 a 1 x y

Representación geométrica del punto (2, 4, 4)

Vectores • Vectores: segmentos de rectas dirigidos en el plano o el espacio con un inicio y un final • Los segmentos de recta que se obtienen uno de otro por traslación representan el mismo vector

Suma Vectorial y Multiplicación por un Escalar • Dadas dos ternas (a 1, a 2, a 3) y (b 1, b 2, b 3) definimos la suma vectorial como • Dadas un escalar y un vector (a 1, a 2, a 3) definimos el producto escalar por medio de

Propiedades de los Vectores • Elemento cero • Inverso aditivo

Propiedades de la Suma y Multiplicación Escalar

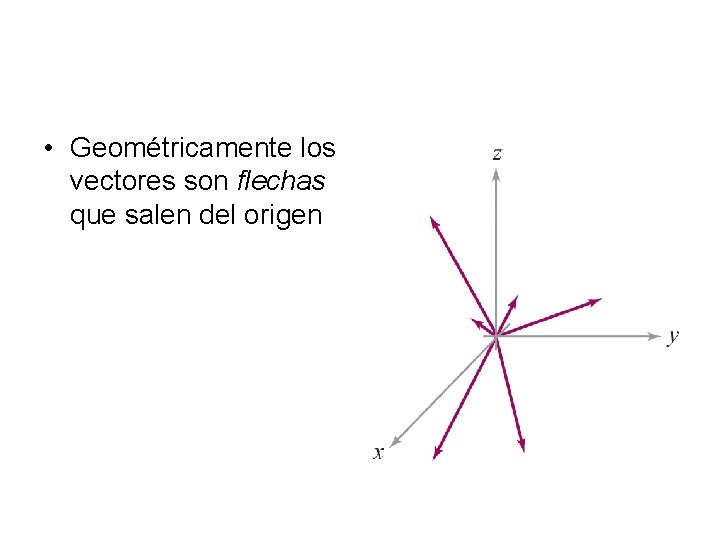
• Geométricamente los vectores son flechas que salen del origen
![Los vectores son segmentos de recta dirigidos en el plano o el espacio representados Los vectores son segmentos de recta dirigidos en [el plano o] el espacio representados](https://slidetodoc.com/presentation_image_h/252b0bbe94b74aa2bdf05e7466e5e313/image-12.jpg)
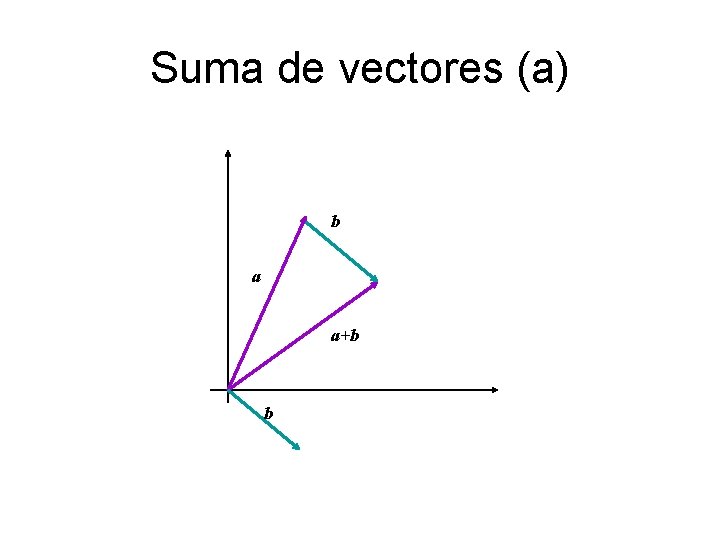
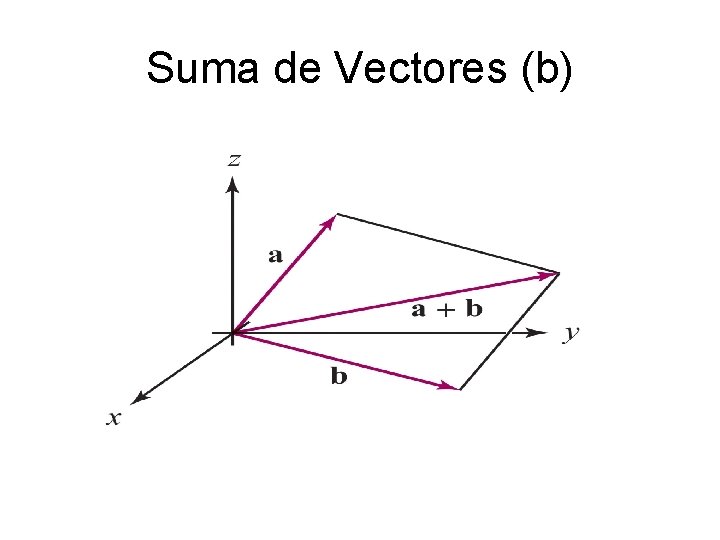
Los vectores son segmentos de recta dirigidos en [el plano o] el espacio representados por segmentos de recta dirigidos con un inicio (cola) y un final (punta). Los segmentos de recta que se obtienen uno de otro por traslación paralela (pero no rotación) representan el mismo vector. Las componentes (a 1, a 2, a 3) de a son las longitudes (dirigidas) de las proyecciones de a a lo largo de los tres ejes coordenados. La suma de dos vectores se obtiene colocándolos final con inicio y trazando el vector que va del inicio al final del segundo.

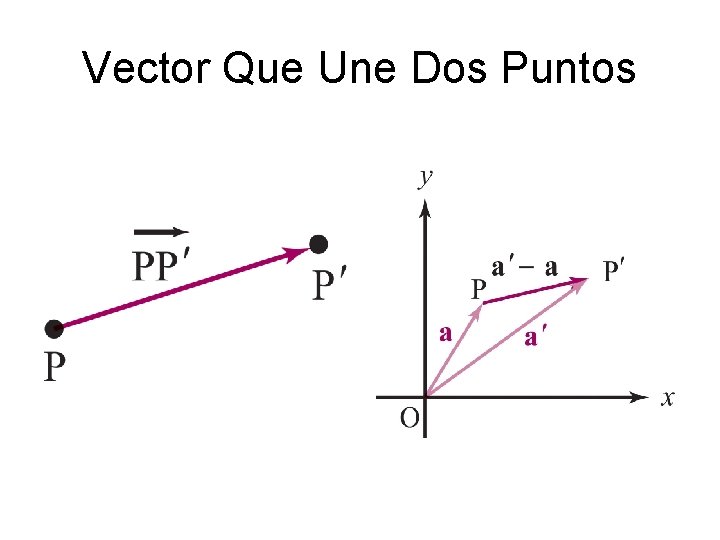
Vector Que Une Dos Puntos

El Vector Que Une Dos Puntos • Si el punto P tiene coordenadas (x, y, z) y P’ tiene coordenadas (x’, y’, z’) entonces el vector PP’ de la punta de P a las punta de P’ tiene componentes

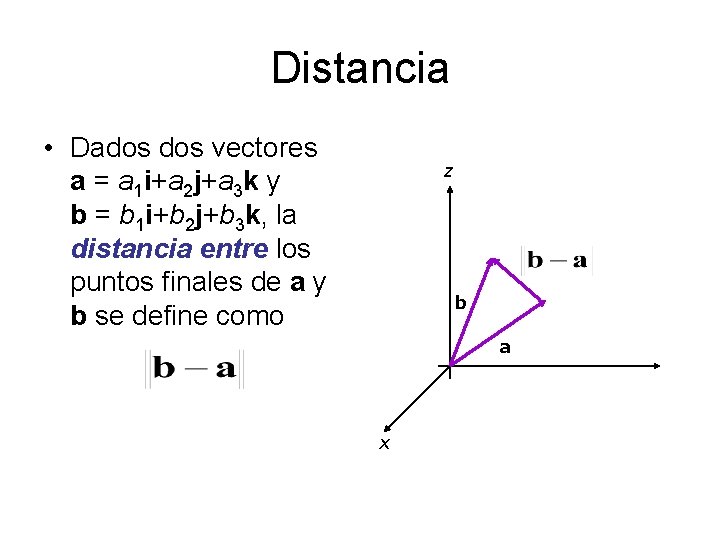
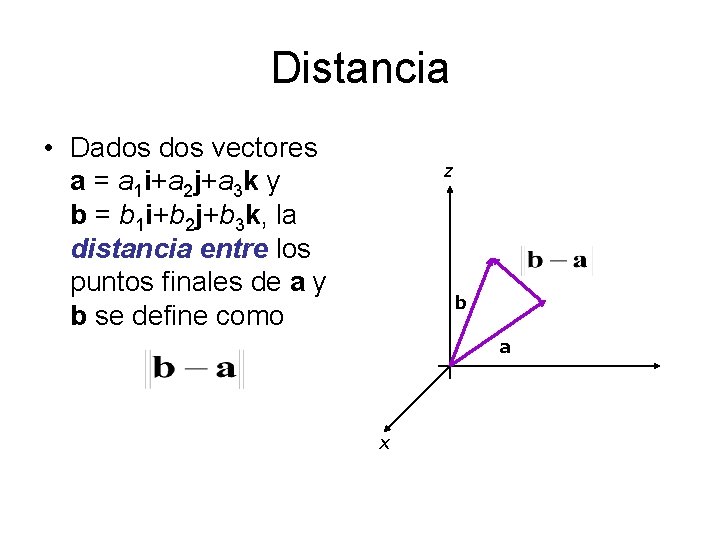
Distancia • Dados vectores a = a 1 i+a 2 j+a 3 k y b = b 1 i+b 2 j+b 3 k, la distancia entre los puntos finales de a y b se define como z b a x

Suma de vectores (a) b a a+b b

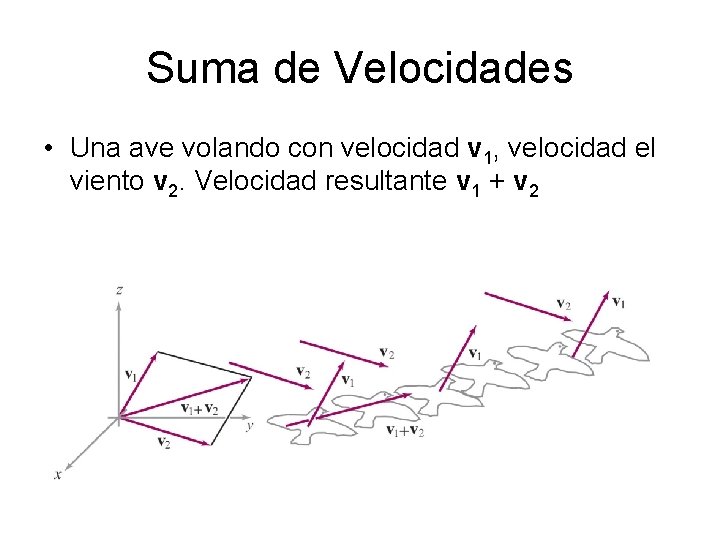
Suma de Velocidades • Una ave volando con velocidad v 1, velocidad el viento v 2. Velocidad resultante v 1 + v 2

Suma de Vectores (b)

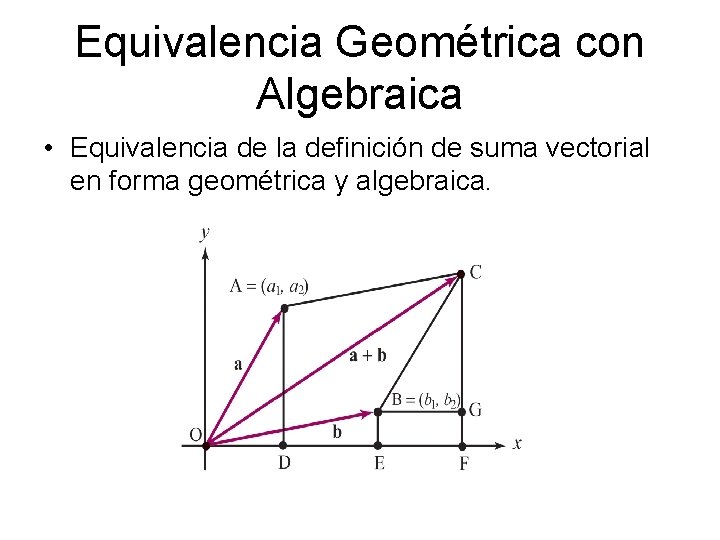
Equivalencia Geométrica con Algebraica • Equivalencia de la definición de suma vectorial en forma geométrica y algebraica.

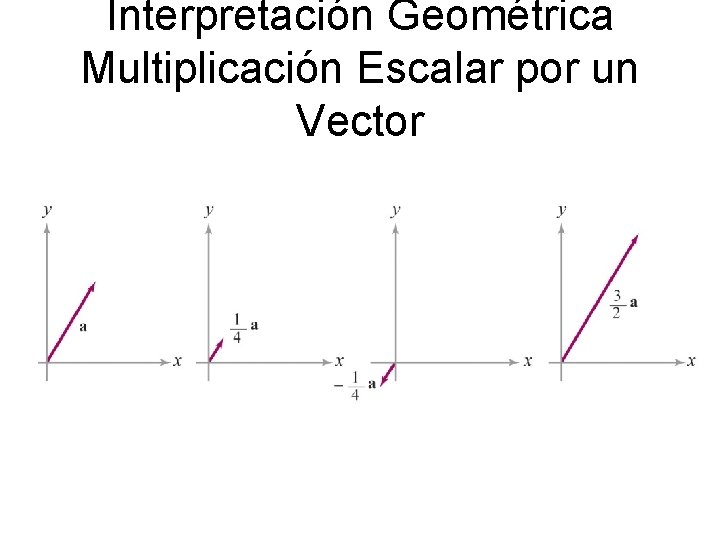
Interpretación Geométrica Multiplicación Escalar por un Vector

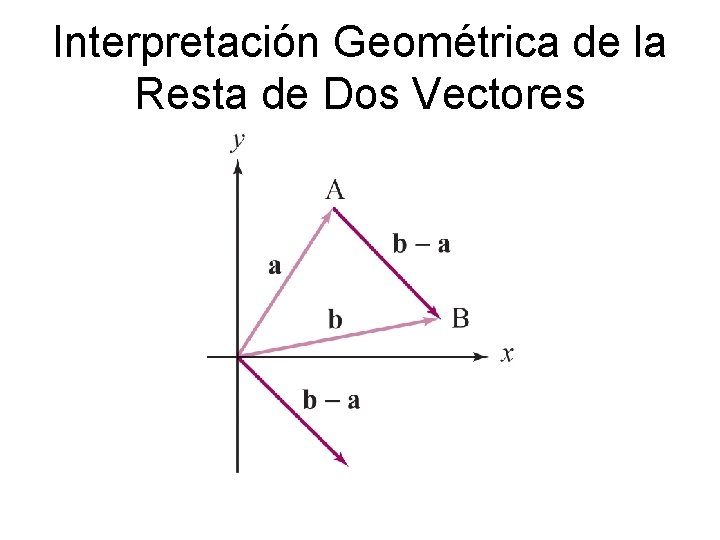
Interpretación Geométrica de la Resta de Dos Vectores

Distancia • Dados vectores a = a 1 i+a 2 j+a 3 k y b = b 1 i+b 2 j+b 3 k, la distancia entre los puntos finales de a y b se define como z b a x

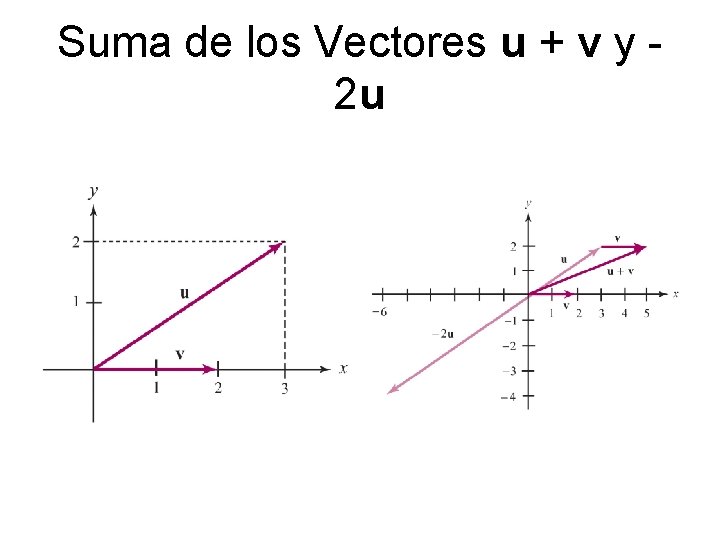
Suma de los Vectores u + v y 2 u

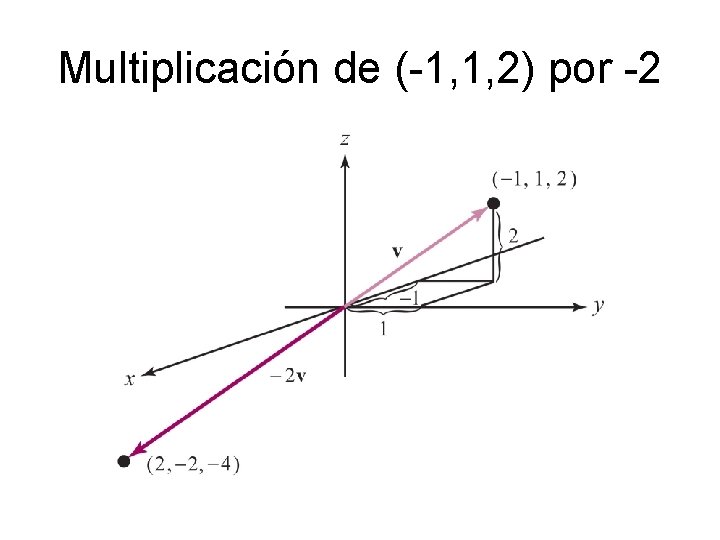
Multiplicación de (-1, 1, 2) por -2

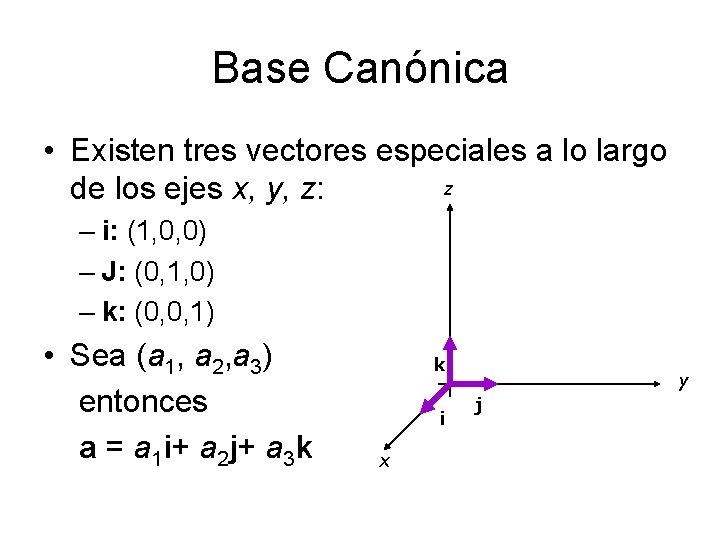
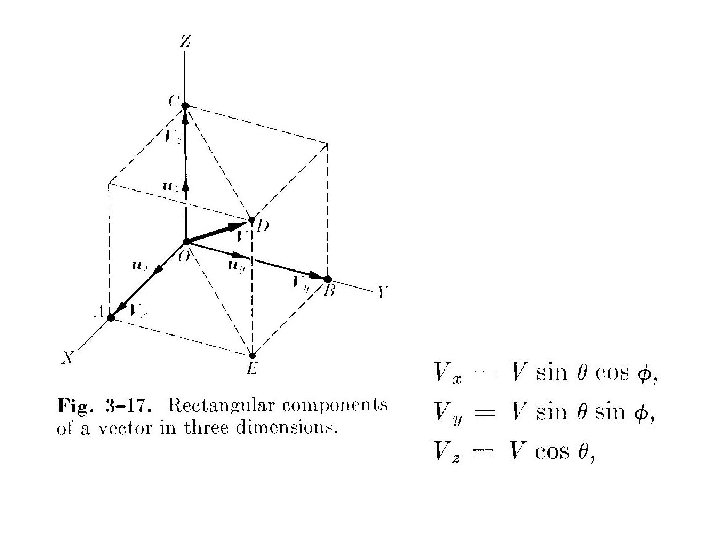
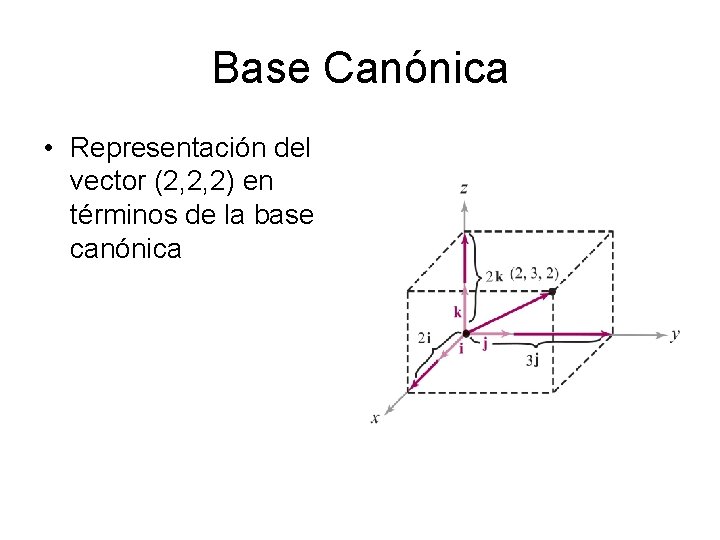
Base Canónica • Existen tres vectores especiales a lo largo z de los ejes x, y, z: – i: (1, 0, 0) – J: (0, 1, 0) – k: (0, 0, 1) • Sea (a 1, a 2, a 3) entonces a = a 1 i+ a 2 j+ a 3 k k i x y j

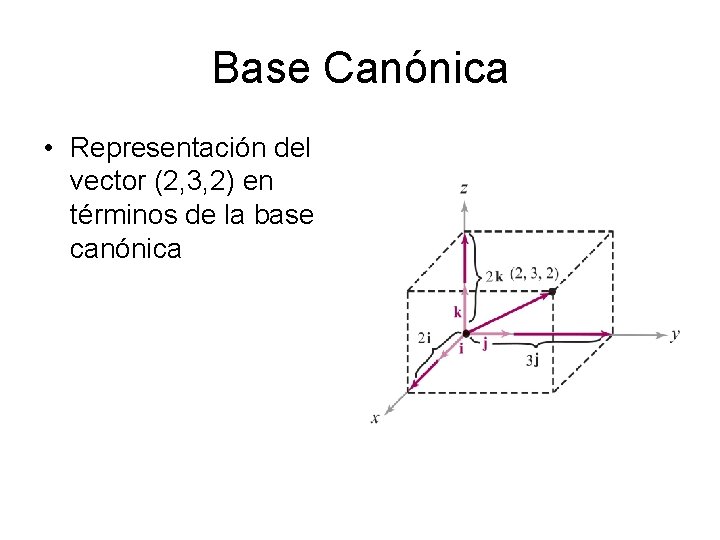
Base Canónica • Representación del vector (2, 3, 2) en términos de la base canónica

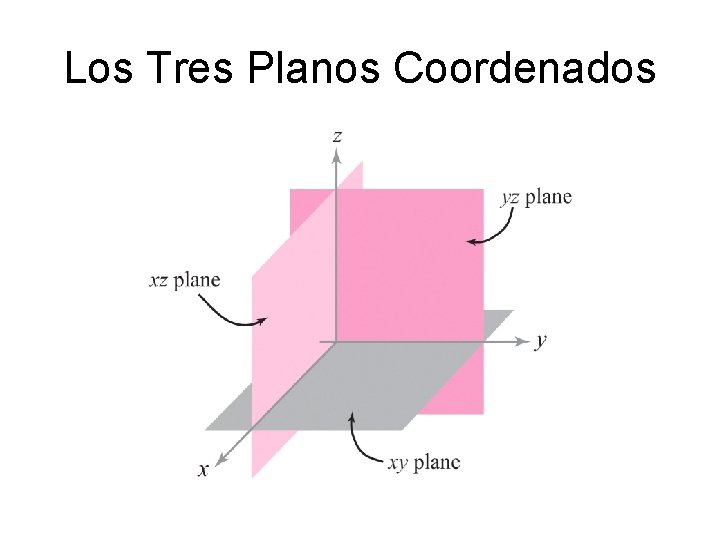
Los Tres Planos Coordenados

Producto Interno • Dados vectores a = a 1 i+a 2 j+a 3 k y b = b 1 i+b 2 j+b 3 k, el producto interno de a y b se define como Nótese que el producto interno es un escalar.

Producto Interno • Propiedades del producto interno. Sean a, b, c vectores en ℝ³ y números reales, entonces

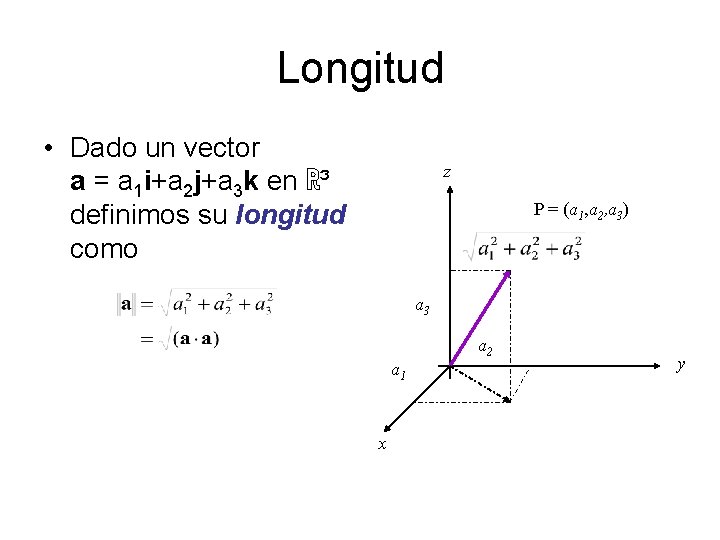
Longitud • Dado un vector a = a 1 i+a 2 j+a 3 k en ℝ³ definimos su longitud como z P = (a 1, a 2, a 3) a 3 a 2 a 1 x y

Vectores Normalizados • Dado el vector a = a 1 i + a 2 j + a 3 k diferente de cero, para normalizarlo forme el vector

Ejemplos • Normalizar el vector v = 15 i – 2 j + 4 k. Solución La normalización del vector v está dada por

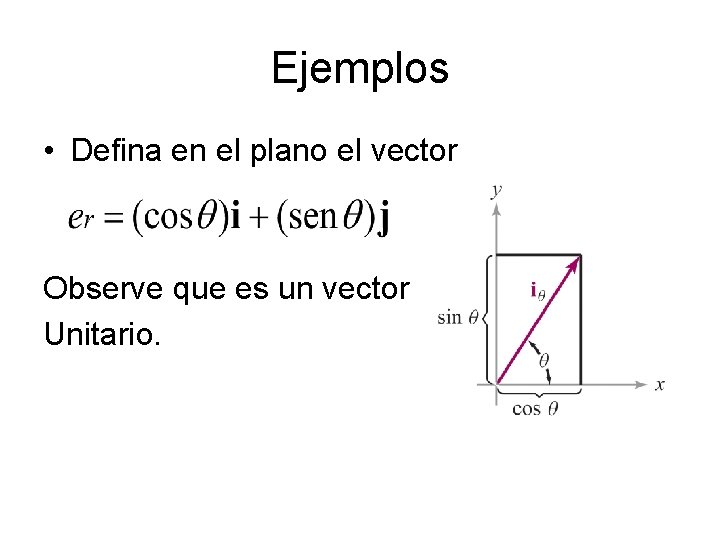
Ejemplos • Defina en el plano el vector Observe que es un vector Unitario.

Vectores Ortogonales • Si a y b son vectores diferentes de cero y es el ángulo entre ellos. Entonces si y sólo si los vectores son ortogonales. • Ejemplo – Los vectores de la base canónica i, j, k, son ortogonales entre si. – Los vectores y son ortogonales.

Vectores Ortonormales

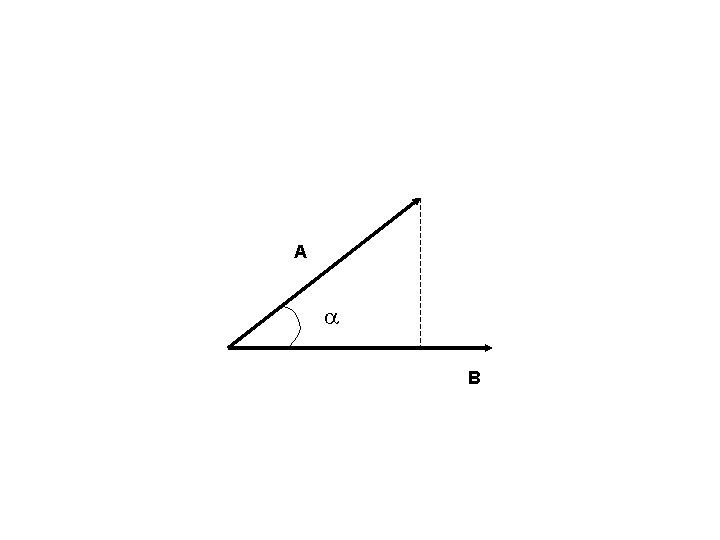
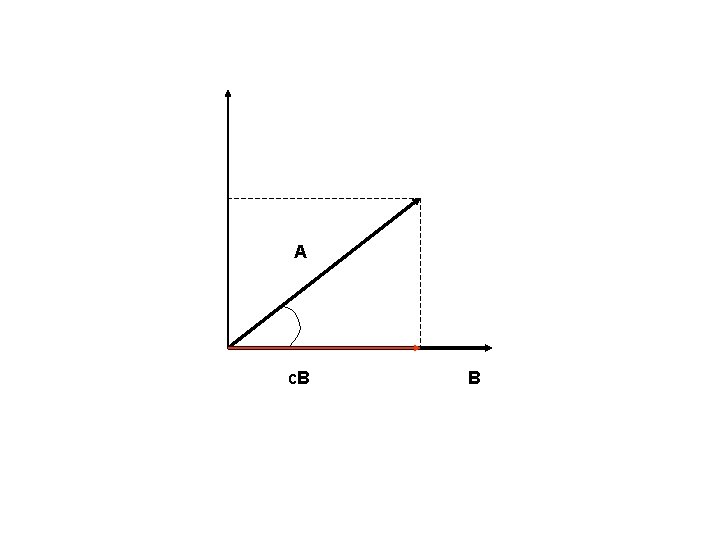
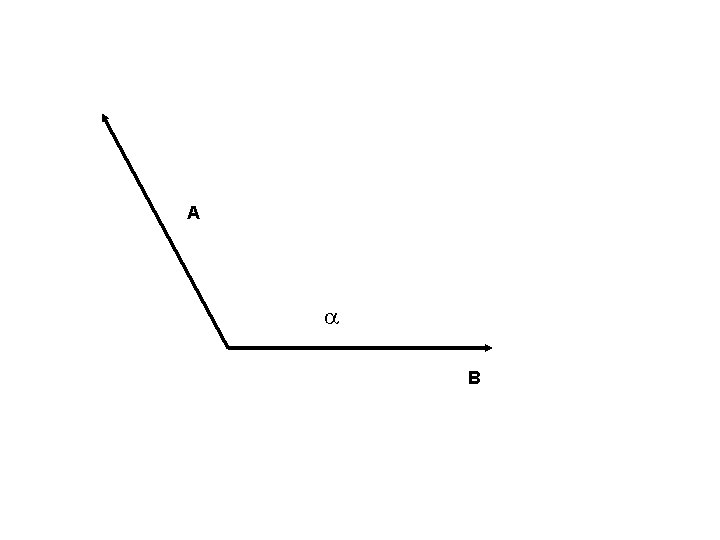
A a B

A c. B B

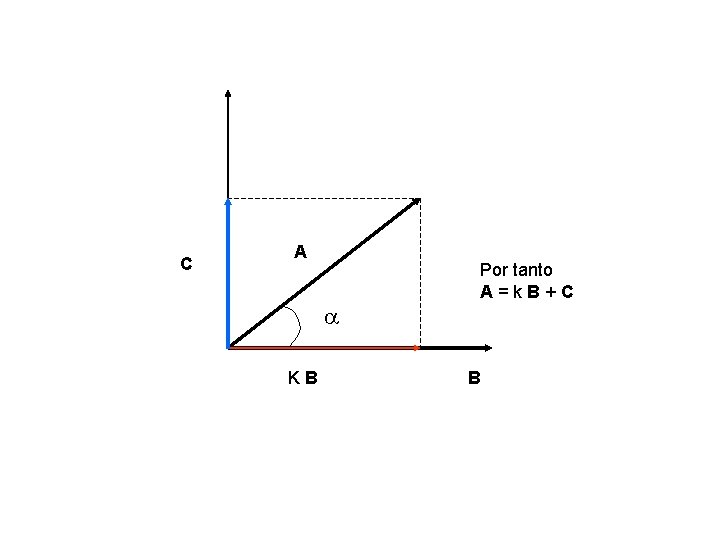
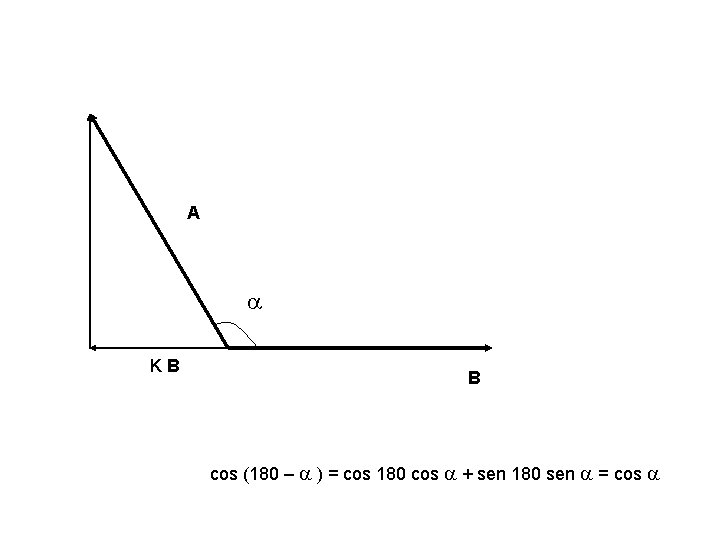
C A a KB Por tanto A=k. B+C B

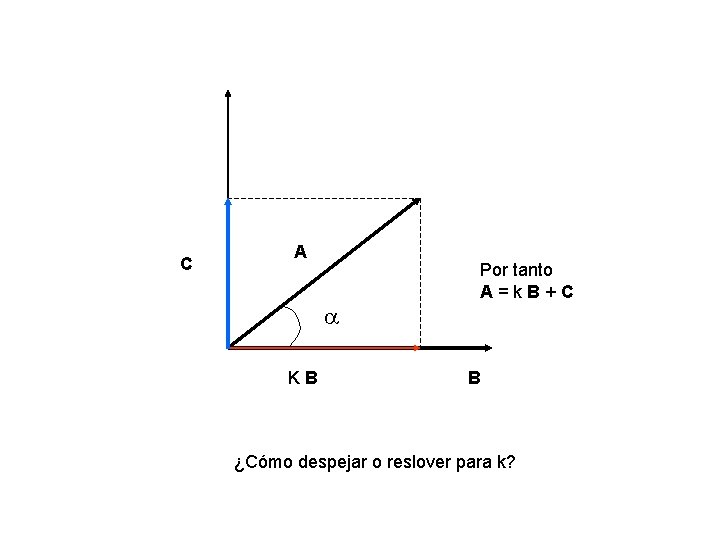
C A a KB Por tanto A=k. B+C B ¿Cómo despejar o reslover para k?

Usemos lo que conocemos: i) Ortogonalidad o perpendicularidad ii) Producto punto

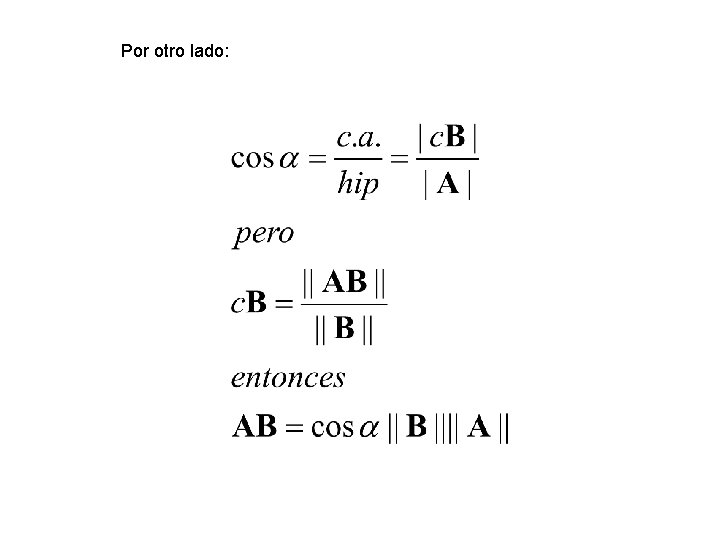
Por otro lado:

A a B

A a KB B cos (180 – a ) = cos 180 cos a + sen 180 sen a = cos a

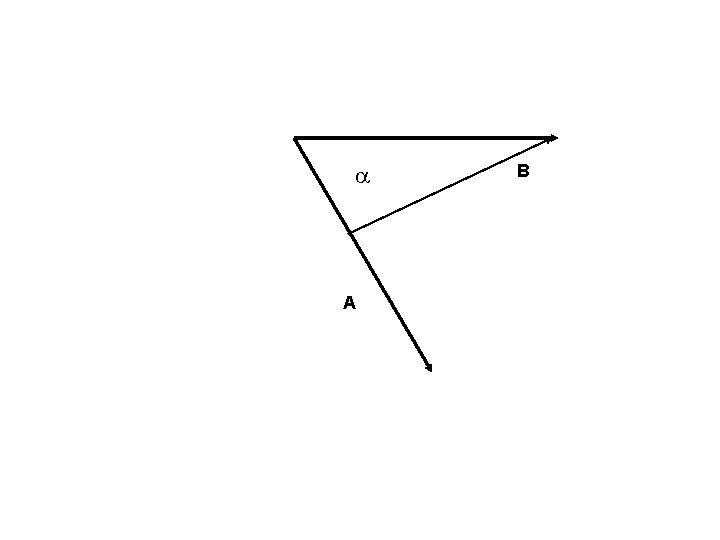
a A B

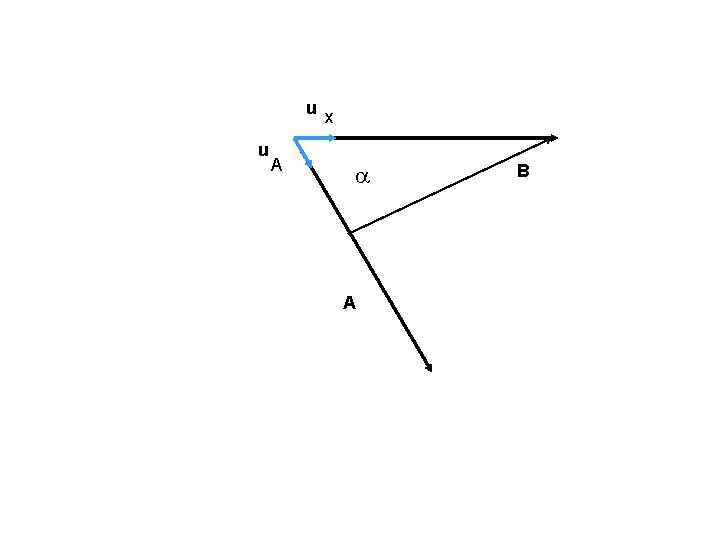
u u A x a A B

Por tanto si A es unitario u B = || u || || B || cos a = Bu Y por tanto si || B || solo escribimos B Bx = B cos a By = B sen a porqué? Y asi B = ux B cos a + uy B sen a = B ( ux cos a + uy sen a )

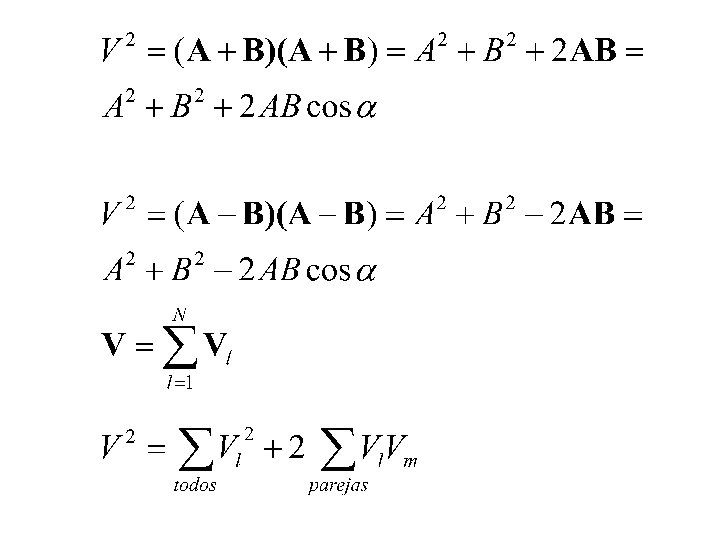

Ejemplos • Calcule el angulo entre los vectores A = 2 i + 3 j – k y B = - i + j + 2 k Solución: Usando

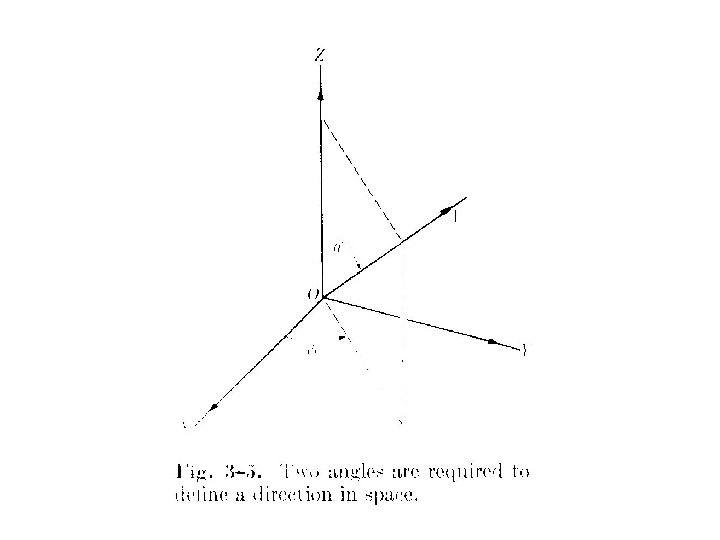
Reflexiones • Ángulo en grados o en radianes • Se mide con respecto a que? • Ejemplo en el Planeta Tierra




Ejemplos • Encuentre los angulos que forma el vector A = 2 i + 3 j + 2 k con los ejes x & z Solución

Base Canónica • Representación del vector (2, 2, 2) en términos de la base canónica

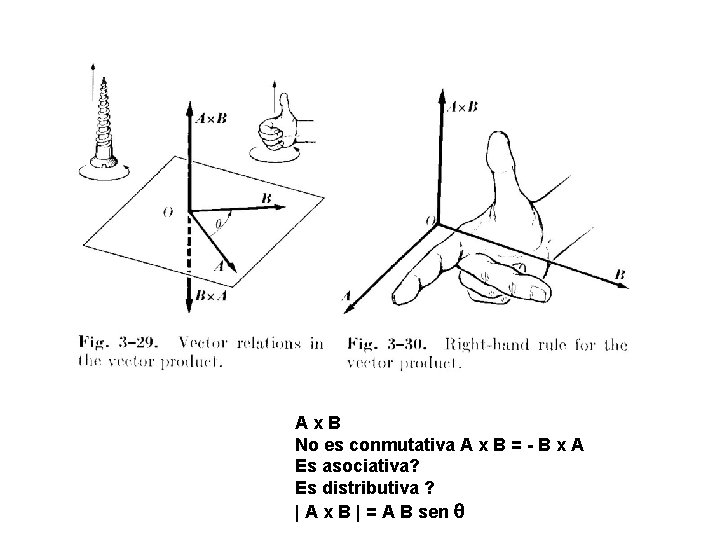
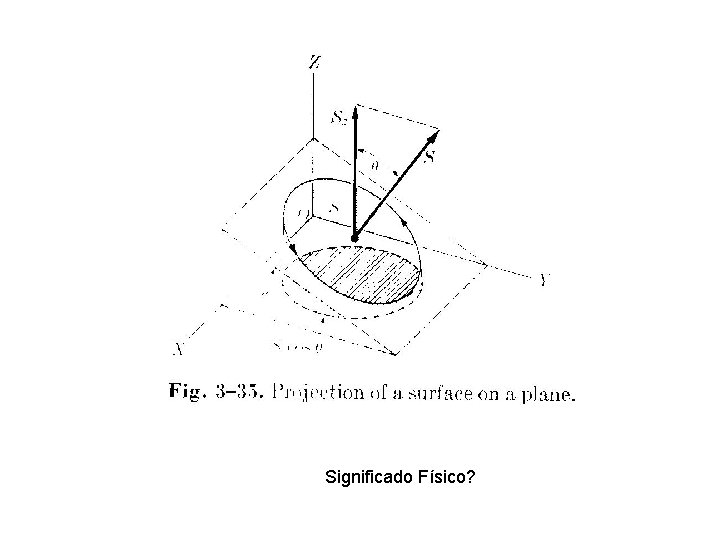
Ax. B No es conmutativa A x B = - B x A Es asociativa? Es distributiva ? | A x B | = A B sen q
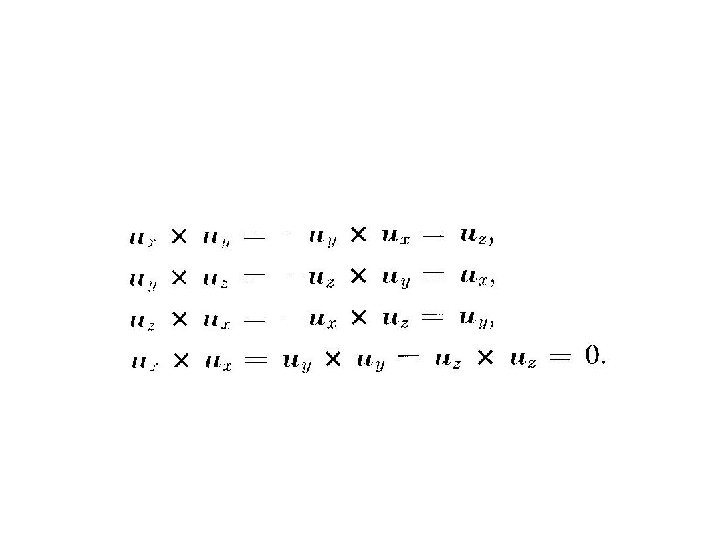
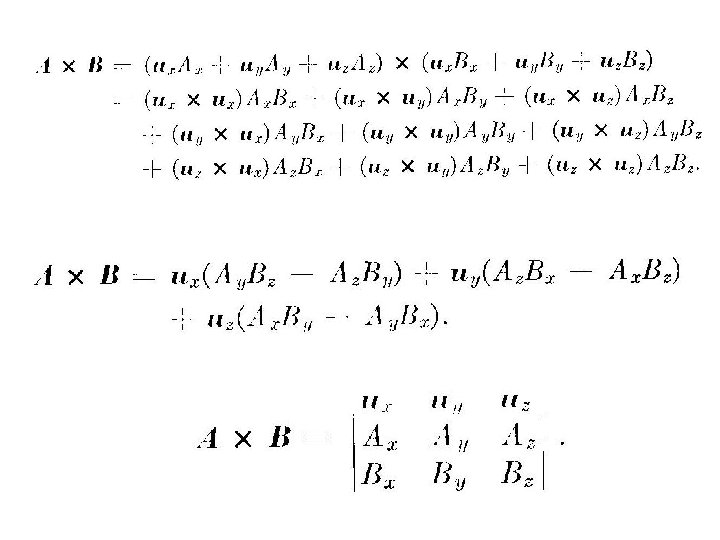

Significado Físico?
 Rogerio marcondes
Rogerio marcondes Rogerio feris
Rogerio feris São softwares aplicativos
São softwares aplicativos Calderas acuotubulares
Calderas acuotubulares Orion magnetrol
Orion magnetrol Yellowstone caldera formation
Yellowstone caldera formation Pirotubular
Pirotubular Caldera 700 wg
Caldera 700 wg What are underground igneous rock bodies called?
What are underground igneous rock bodies called? Objetivo de una caldera
Objetivo de una caldera Fsica
Fsica Vectores unitarios
Vectores unitarios Fsica
Fsica Produto escalar
Produto escalar Fsica
Fsica Fsica
Fsica Ed
Ed Formula centripeta
Formula centripeta Leis de newton
Leis de newton Expresion vectorial
Expresion vectorial Sistema termodinamico
Sistema termodinamico Fsica
Fsica Fsica
Fsica Modulo direção sentido
Modulo direção sentido Division de la fisica clasica
Division de la fisica clasica Fsica
Fsica Mruv
Mruv Ejemplos de electrostática
Ejemplos de electrostática Vector unitario
Vector unitario Fsica
Fsica Fsica
Fsica Apoyo fijo movil y empotrado
Apoyo fijo movil y empotrado Fsica
Fsica Mapa mental movimento uniforme
Mapa mental movimento uniforme Relação fonética e gráfica entre as palavras
Relação fonética e gráfica entre as palavras Fonemas y monemas
Fonemas y monemas Observa las siguientes gráficas
Observa las siguientes gráficas El numero total de placas distintas que se pueden fabricar
El numero total de placas distintas que se pueden fabricar Gráficas mrua 2 eso
Gráficas mrua 2 eso Ecuación itinerario mrua
Ecuación itinerario mrua Multiplicación de logaritmos
Multiplicación de logaritmos Limite inferior y superior
Limite inferior y superior Puntos consecutivos
Puntos consecutivos Conjuntos por comprensión y extensión
Conjuntos por comprensión y extensión Graficas de funciones cubicas
Graficas de funciones cubicas Movimiento rectilineo uniforme grafica
Movimiento rectilineo uniforme grafica Grafica de muestreo
Grafica de muestreo Oraciones coordinadas
Oraciones coordinadas Gráficas de
Gráficas de O mapa é uma das mais antigas formas gráficas
O mapa é uma das mais antigas formas gráficas Cotangente en excel
Cotangente en excel Prueba de hipotesis graficas
Prueba de hipotesis graficas Dadas las siguientes graficas cuales son funciones
Dadas las siguientes graficas cuales son funciones Grafico lanzamiento vertical hacia abajo
Grafico lanzamiento vertical hacia abajo Buscar cualquier imagen
Buscar cualquier imagen