Summer School for Integrated Computational Materials Education 2015

Summer School for Integrated Computational Materials Education 2015 Computational Mechanics: Basic Concepts and Finite Element Method Katsuyo Thornton Materials Science & Engineering University of Michigan

This lecture will. . . • • Provide you with the general background related to the Computational Mechanics Module. Topics o Brief review of continuum mechanics of an elastic solid o Finite element method for mechanics problems (Stiffness method) o Finite element method as a general partial differential equation solver (brief, if time allows) Summer School for Integrated Computational Materials Education Ann Arbor, Michigan, June 15 -26, 2015

Continuum Mechanics • The study of the physics of continuous materials From Wikipedia Summer School for Integrated Computational Materials Education Ann Arbor, Michigan, June 15 -26, 2015

Continuum Mechanics • The study of the physics of continuous materials Summer School for Integrated Computational Materials Education Ann Arbor, Michigan, June 15 -26, 2015

Basic Concepts of (Static) Elasticity • An elastically deformed material returns to its original shape upon the release of applied force – reversible. • Compare to plasticity – irreversible changes to materials. • Basic equation governing elasticity considers: – Mechanical equilibrium (Force must balance) – Constitutive equation (What reaction does material exhibit in response to strain? ) • Will first examine one dimensional system. Summer School for Integrated Computational Materials Education Ann Arbor, Michigan, June 15 -26, 2015

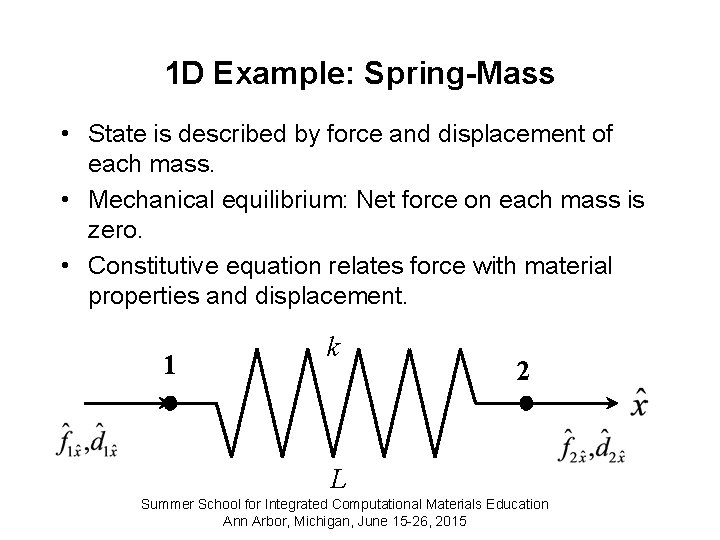
1 D Example: Spring-Mass • State is described by force and displacement of each mass. • Mechanical equilibrium: Net force on each mass is zero. • Constitutive equation relates force with material properties and displacement. 1 k 2 L Summer School for Integrated Computational Materials Education Ann Arbor, Michigan, June 15 -26, 2015

1 D Example: Spring-Mass • Mechanical equilibrium: net force at mass i • Constitutive equation of linear elasticity (Hooke’s Law) 1 k 2 L Summer School for Integrated Computational Materials Education Ann Arbor, Michigan, June 15 -26, 2015

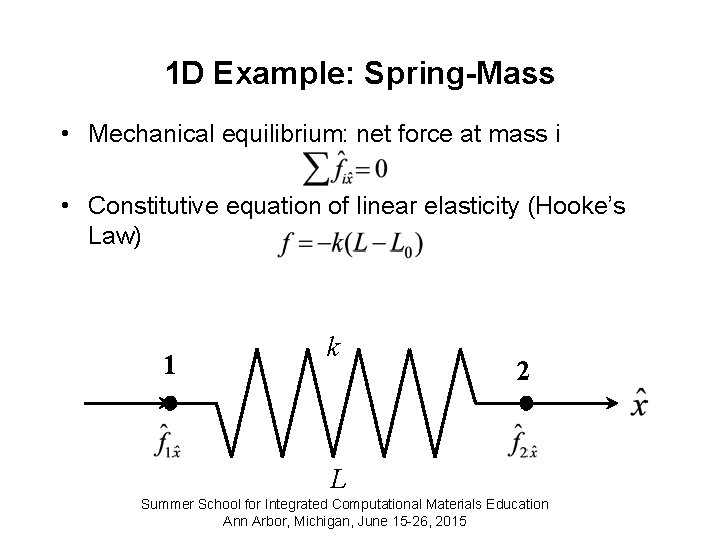
Solid Mechanics: 3 D • Consider a volume element inside a body. From Wikipedia Summer School for Integrated Computational Materials Education Ann Arbor, Michigan, June 15 -26, 2015

Solid Mechanics: 3 D • In multi-dimension, deformation along one direction leads to deformation along another direction. • Green: undeformed body • Red: after tensile strain Summer School for Integrated Computational Materials Education Ann Arbor, Michigan, June 15 -26, 2015

Tensors • Multidimensional array of numbers with respect to a basis (including scalar) • Orders of tensors – Scalar, 0 th-order tensor, f – Vector, 1 st-order tensor, v = [f 1, f 2, f 3, . . . ] – Matrix, 2 nd-order tensor – i. e. , the order of a tensor can be understood as the dimension • The number of elements in each dimension is usually determined by the spatial dimension associated with the problem. Summer School for Integrated Computational Materials Education Ann Arbor, Michigan, June 15 -26, 2015

Stress Tensor • Stress is a second-order tensor. Summer School for Integrated Computational Materials Education Ann Arbor, Michigan, June 15 -26, 2015

Strain • Strain results from deformation of a body. • Strain is a gradient of displacement. – Constant displacement DOES NOT lead to deformation. – Constant strain is a uniform stretch/compression of the body. – In a spring-mass system, the displacement of the mass is measured away from the equilibrium position. The spring can be viewed as having to experience uniform strain. • Strain tensor Summer School for Integrated Computational Materials Education Ann Arbor, Michigan, June 15 -26, 2015

Stress & Strain • Stress is equivalent to the force in the spring-mass system. – Stress has a unit of force per unit area. • Strain is related to the displacement of the mass. – Strain is dimensionless, as it is the gradient of displacement (unit of length) with respect to the position (unit of length). Summer School for Integrated Computational Materials Education Ann Arbor, Michigan, June 15 -26, 2015

Linear Elasticity • Equivalent to Hooke’s Law for springs. • In the most general form • Repeated indices imply summation. • For isotropic materials, the elastic constants can be reduced to K and m are the bulk modulus and shear modulus. Summer School for Integrated Computational Materials Education Ann Arbor, Michigan, June 15 -26, 2015

Elasticity vs. Plasticity • When a material experiences a large deformation, its atomic constituency arranges itself in such a way that it will not recover to the original state. – Bond breaking – Dislocation motion • Plastic deformation is a challenging multiscale problem! Summer School for Integrated Computational Materials Education Ann Arbor, Michigan, June 15 -26, 2015

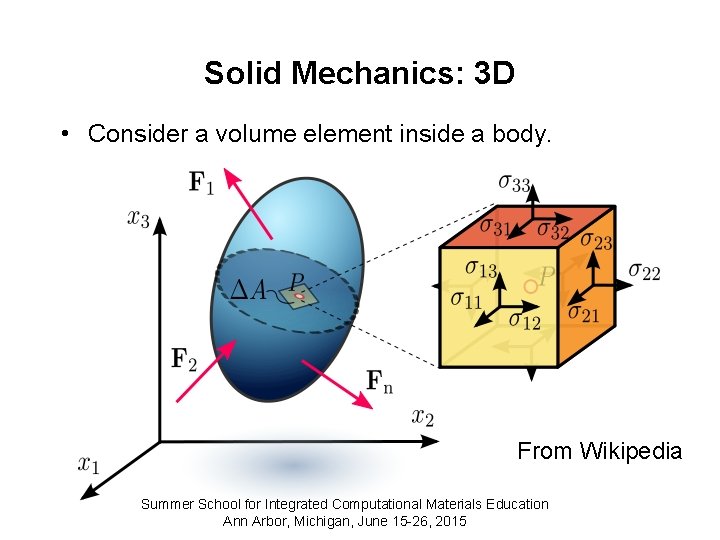
Force Balance • Change in stress with respect to position is the unbalanced force. • Force balance in 3 D or Summer School for Integrated Computational Materials Education Ann Arbor, Michigan, June 15 -26, 2015

How Do We Solve the Equations • Once you obtain a PDE, there are many ways to solve the problem. • Finite Element Analysis or Finite Element Method has been the dominant approach in computational solid mechanics. – Relatively good convergence (higher accuracy with fewer mesh points). – Internal boundary conditions. • There are other methods that allow solutions, including a reformulation of the original equation, which can easily be solved using the finite difference method. Summer School for Integrated Computational Materials Education Ann Arbor, Michigan, June 15 -26, 2015

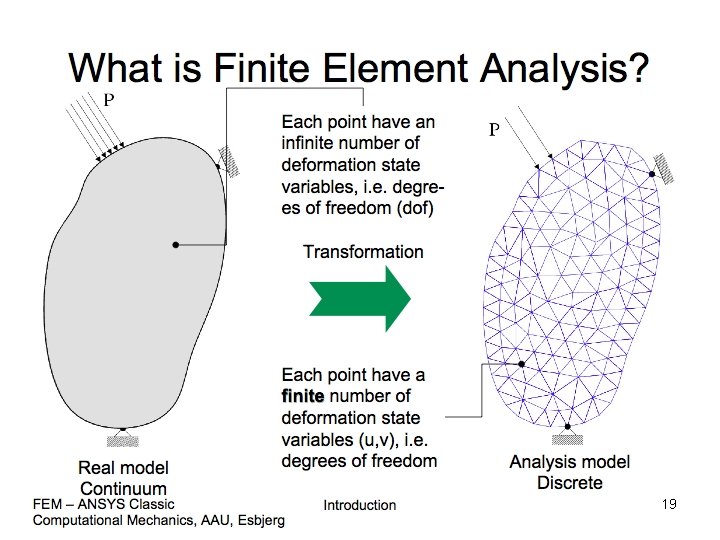
What is FEM? The finite element method is a numerical method to solve problems of engineering and physics. • Useful for problems with complicated geometries, loadings, and material properties where analytical solutions cannot be obtained. • Mathematically, the PDE is converted to its variational (integral) form. An approximate solution is given by a linear combination of trial functions. The solution is given by error reduction. • Physically, it is equivalent to dividing up a system into smaller pieces (elements) where each piece follows the law of nature. • Summer School for Integrated Computational Materials Education Ann Arbor, Michigan, June 15 -26, 2015

Summer School for Integrated Computational Materials Education Ann Arbor, Michigan, June 15 -26, 2015 19

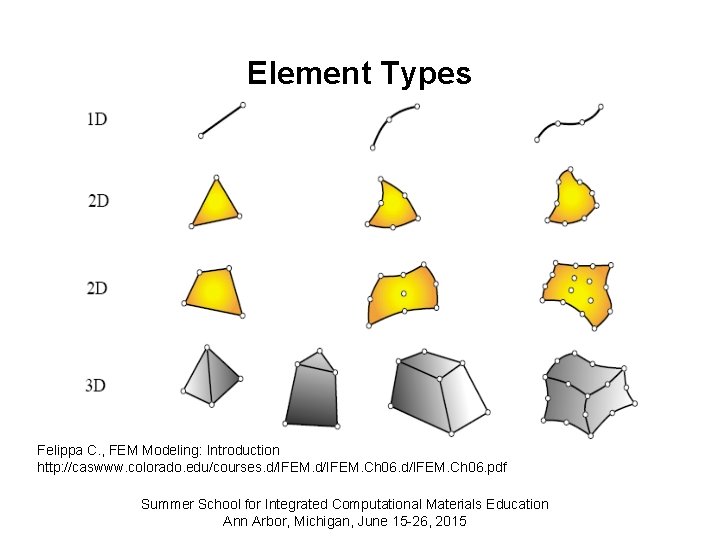
Discretizations • Model a physical body by dividing it into an equivalent system of smaller bodies or units (finite elements) interconnected at points common to two or more elements (nodes or nodal points) and/or boundary lines and/or surfaces. Summer School for Integrated Computational Materials Education Ann Arbor, Michigan, June 15 -26, 2015

Element Types Felippa C. , FEM Modeling: Introduction http: //caswww. colorado. edu/courses. d/IFEM. Ch 06. pdf Summer School for Integrated Computational Materials Education Ann Arbor, Michigan, June 15 -26, 2015

Advantages • • Irregular Boundaries General Loads Different Materials Boundary Conditions Variable Element Size Easy Modification Dynamics Nonlinear Problems (Geometric or Material) Summer School for Integrated Computational Materials Education Ann Arbor, Michigan, June 15 -26, 2015

Typical Applications of FEM • • • Structural/Stress Analysis Fluid Flow Heat Transfer Electro-Magnetic Fields Soil Mechanics Acoustics Summer School for Integrated Computational Materials Education Ann Arbor, Michigan, June 15 -26, 2015

Steps in FEM 1. 2. 3. 4. 5. 6. 7. 8. Discretize and Select Element Type Select a Displacement Function Define Strain/Displacement and Stress/Strain Relationships Derive Element Stiffness Matrix & Eqs. Assemble Equations and Introduce B. C. s Solve for the Unknown Displacements Calculate Element Stresses and Strains Interpret the Results Summer School for Integrated Computational Materials Education Ann Arbor, Michigan, June 15 -26, 2015

Stiffness Method A physically based FEM Divide up a system into smaller pieces (elements) where each piece follow the law of nature

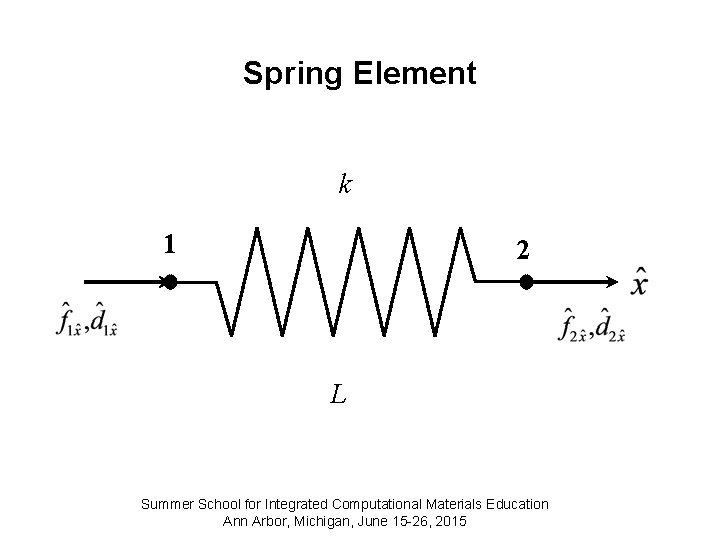
Definitions for this section For an element, a stiffness matrix is a matrix such that where relates local coordinates and nodal displacements to local forces of a single element. Bold denotes vector/matrices. Summer School for Integrated Computational Materials Education Ann Arbor, Michigan, June 15 -26, 2015

Spring Element k 1 2 L Summer School for Integrated Computational Materials Education Ann Arbor, Michigan, June 15 -26, 2015

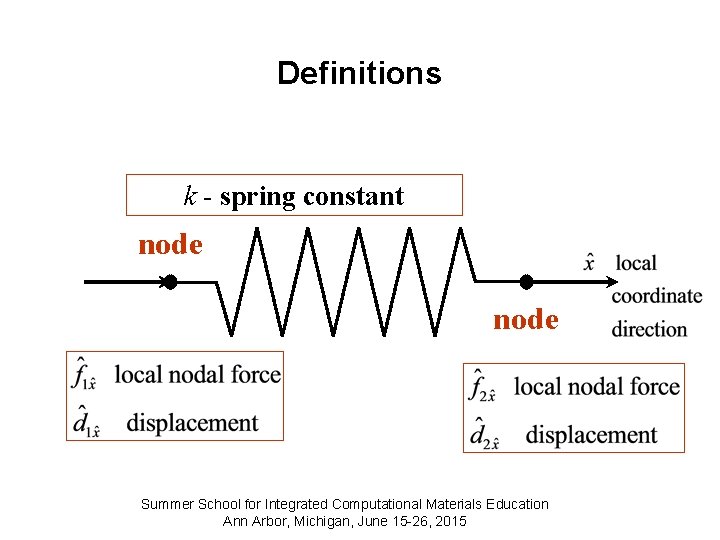
Definitions k - spring constant node Summer School for Integrated Computational Materials Education Ann Arbor, Michigan, June 15 -26, 2015

Stiffness Relationship for a Spring Summer School for Integrated Computational Materials Education Ann Arbor, Michigan, June 15 -26, 2015

Steps in Process 1) 2) 3) 4) 5) 6) 7) 8) Discretize and Select Element Type Select a Displacement Function Define Strain/Displacement and Stress/Strain Relationships Derive Element Stiffness Matrix & Eqs. Assemble Equations and Introduce B. C. s Solve for the Unknowns (Displacements) Calculate Element Stresses and Strains Interpret the Results Summer School for Integrated Computational Materials Education Ann Arbor, Michigan, June 15 -26, 2015

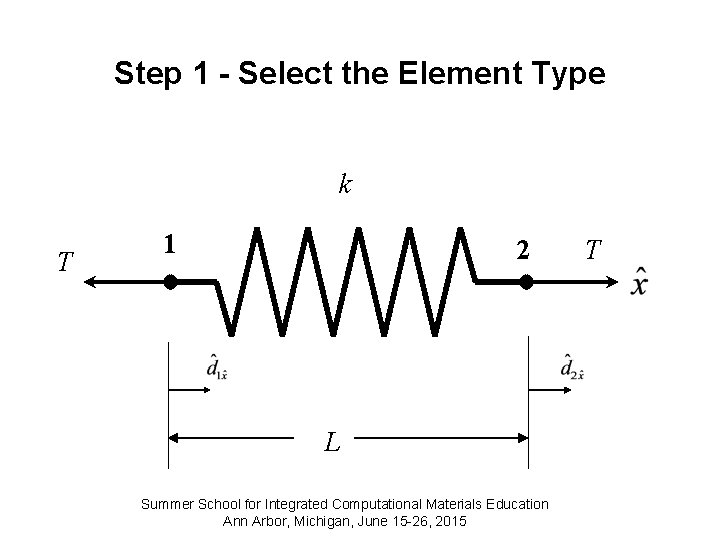
Step 1 - Select the Element Type k T 1 2 L Summer School for Integrated Computational Materials Education Ann Arbor, Michigan, June 15 -26, 2015 T

Step 2 - Select a Displacement Function Assume a displacement function Assume a linear function. Number of coefficients = number of local d-o-f (degree of freedom) Write in matrix form. Summer School for Integrated Computational Materials Education Ann Arbor, Michigan, June 15 -26, 2015

Express as function of and Solve for a 2 : Summer School for Integrated Computational Materials Education Ann Arbor, Michigan, June 15 -26, 2015

Substituting back into: Yields: Summer School for Integrated Computational Materials Education Ann Arbor, Michigan, June 15 -26, 2015

In matrix form: or Summer School for Integrated Computational Materials Education Ann Arbor, Michigan, June 15 -26, 2015

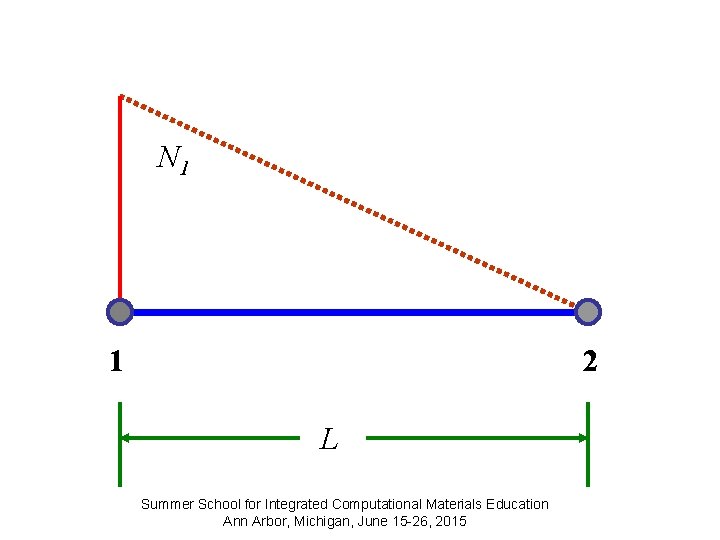
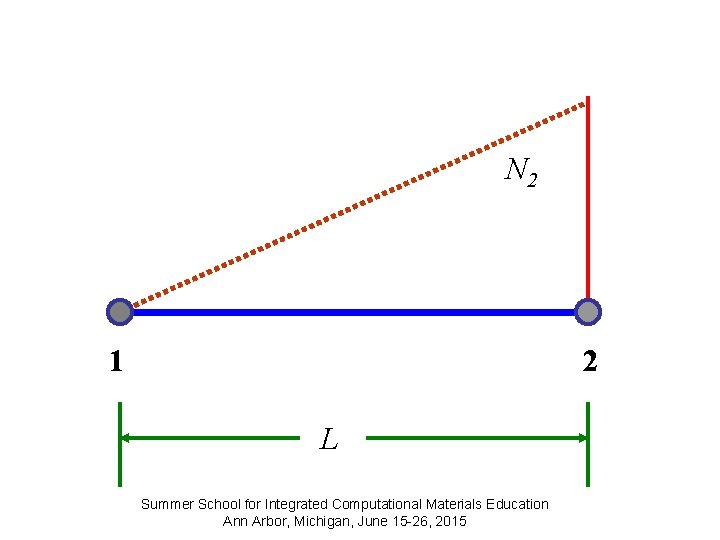
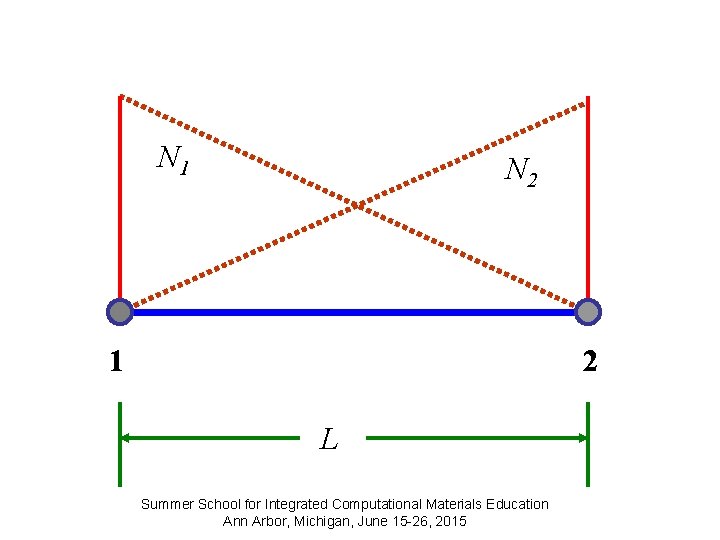
Shape Functions N 1 and N 2 are called Shape Functions or Interpolation Functions. They express the shape of the assumed displacements. N 1 =1 N 2 =0 at node 1 N 1 =0 N 2 =1 at node 2 N 1 + N 2 =1 Summer School for Integrated Computational Materials Education Ann Arbor, Michigan, June 15 -26, 2015

N 1 1 2 L Summer School for Integrated Computational Materials Education Ann Arbor, Michigan, June 15 -26, 2015

N 2 1 2 L Summer School for Integrated Computational Materials Education Ann Arbor, Michigan, June 15 -26, 2015

N 1 N 2 1 2 L Summer School for Integrated Computational Materials Education Ann Arbor, Michigan, June 15 -26, 2015

Step 3 - Define Strain/Displacement and Stress/Strain Relationships where T - tensile force - total elongation Summer School for Integrated Computational Materials Education Ann Arbor, Michigan, June 15 -26, 2015

Step 4 - Derive the Element Stiffness Matrix and Equations Summer School for Integrated Computational Materials Education Ann Arbor, Michigan, June 15 -26, 2015

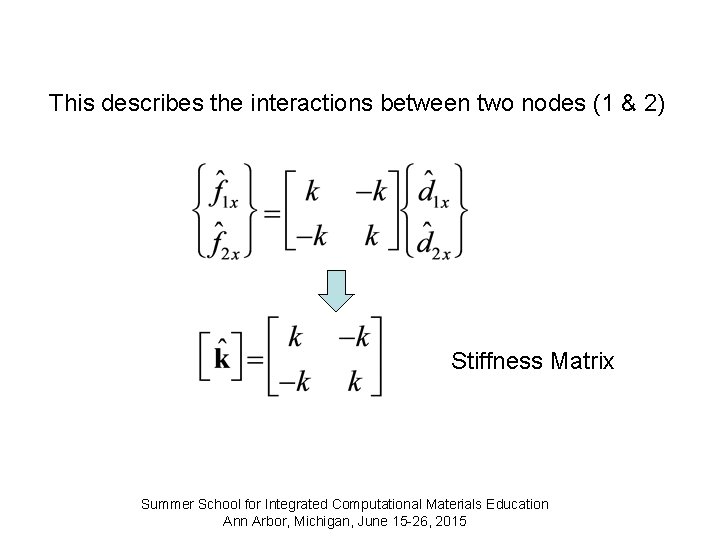
This describes the interactions between two nodes (1 & 2) Stiffness Matrix Summer School for Integrated Computational Materials Education Ann Arbor, Michigan, June 15 -26, 2015

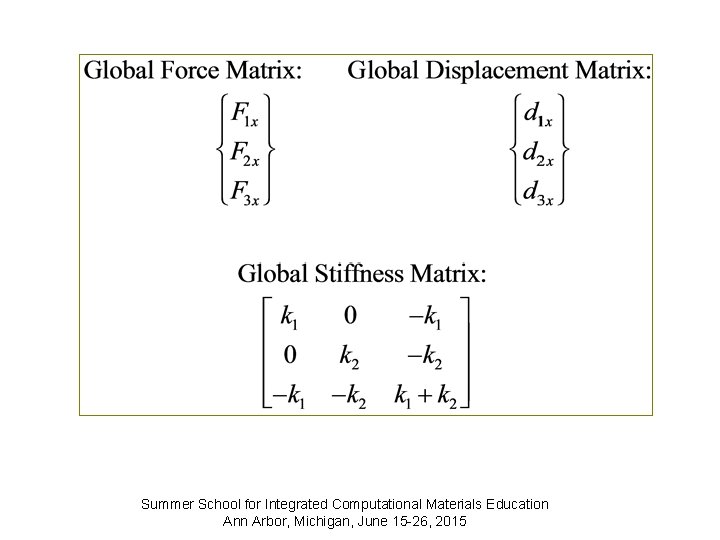
Step 5 - Assemble the Element Equations to Obtain the Global Equations and Introduce the B. C. Note: not simple addition! An example later. Summer School for Integrated Computational Materials Education Ann Arbor, Michigan, June 15 -26, 2015

Step 6 - Solve for Nodal Displacements Summer School for Integrated Computational Materials Education Ann Arbor, Michigan, June 15 -26, 2015

Step 7 - Solve for Element Forces Once displacements at each node are known, then substitute back into element stiffness equations to obtain element nodal forces. Summer School for Integrated Computational Materials Education Ann Arbor, Michigan, June 15 -26, 2015

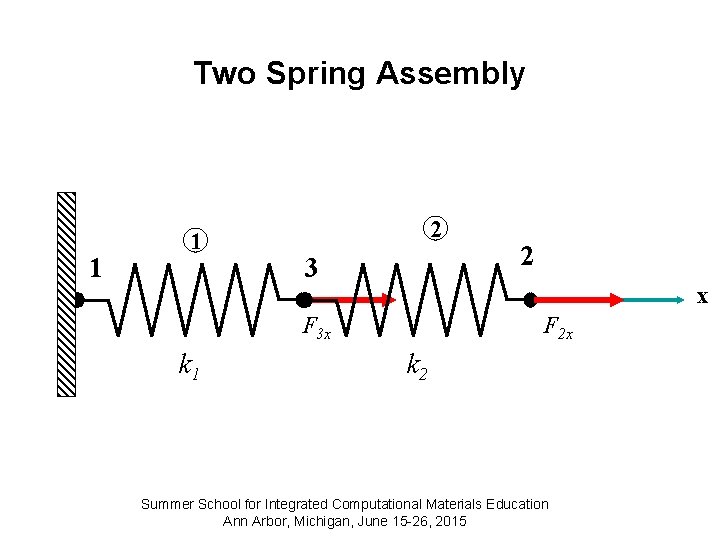
Two Spring Assembly 1 1 2 3 x F 3 x k 1 2 F 2 x k 2 Summer School for Integrated Computational Materials Education Ann Arbor, Michigan, June 15 -26, 2015

Summer School for Integrated Computational Materials Education Ann Arbor, Michigan, June 15 -26, 2015

Continuity/Compatibility Condition Elements 1 and 2 remain connected at node 3. This is called the continuity or compatibility requirement. Summer School for Integrated Computational Materials Education Ann Arbor, Michigan, June 15 -26, 2015

(Includes only those from springs) Summer School for Integrated Computational Materials Education Ann Arbor, Michigan, June 15 -26, 2015

Summer School for Integrated Computational Materials Education Ann Arbor, Michigan, June 15 -26, 2015

Summer School for Integrated Computational Materials Education Ann Arbor, Michigan, June 15 -26, 2015

Assembly of [K] An Alternative Method 1 1 2 3 F 3 x k 1 2 x F 2 x k 2 Summer School for Integrated Computational Materials Education Ann Arbor, Michigan, June 15 -26, 2015

Assembly of [K] - An Alternative Method Summer School for Integrated Computational Materials Education Ann Arbor, Michigan, June 15 -26, 2015

Expand Local [k] matrices to Global Size Summer School for Integrated Computational Materials Education Ann Arbor, Michigan, June 15 -26, 2015

Force Equilibrium Summer School for Integrated Computational Materials Education Ann Arbor, Michigan, June 15 -26, 2015

Summer School for Integrated Computational Materials Education Ann Arbor, Michigan, June 15 -26, 2015

Summer School for Integrated Computational Materials Education Ann Arbor, Michigan, June 15 -26, 2015

Compatibility Summer School for Integrated Computational Materials Education Ann Arbor, Michigan, June 15 -26, 2015

Boundary Conditions (B. C. s) • Must Specify B. C. s to prohibit rigid body motion. • Two type of B. C. s – Homogeneous - displacements = 0 – Nonhomogeneous - displacements = nonzero value Summer School for Integrated Computational Materials Education Ann Arbor, Michigan, June 15 -26, 2015

1 1 2 3 F 3 x k 1 2 x F 2 x k 2 Summer School for Integrated Computational Materials Education Ann Arbor, Michigan, June 15 -26, 2015

Homogeneous B. C. ’s • Delete row and column corresponding to B. C. • Solve for unknown displacements. • Compute unknown forces (reactions) from original (unmodified) stiffness matrix. Summer School for Integrated Computational Materials Education Ann Arbor, Michigan, June 15 -26, 2015

Example: Homogeneous BC, d 1 x=0 Summer School for Integrated Computational Materials Education Ann Arbor, Michigan, June 15 -26, 2015

Beyond the Stiffness Method • • The stiffness method provides a good model for solid mechanics problems. However, it is unclear how the method could be applied to a diverse range of problems important in MSE. Now, we will briefly learn about using FEM to solve a partial differential equation (diffusion equation). The method is called the Method of Minimal Weighted Residual (MWR). Summer School for Integrated Computational Materials Education Ann Arbor, Michigan, June 15 -26, 2015

Model Equation: Steady-State Diffusion Equation • Consider dimensional steady-state diffusion equation with source term q(x): • For illustration, we restrict ourselves to 1 D: Summer School for Integrated Computational Materials Education Ann Arbor, Michigan, June 15 -26, 2015

Approximate Solution • we express the approximate solution as a linear combination of basis functions: where ai are constants. • For accuracy, the best bases are those that behave similarly to the solution. However, for computational efficiency, simpler bases (such as a linear function) are often a better fit. Summer School for Integrated Computational Materials Education Ann Arbor, Michigan, June 15 -26, 2015

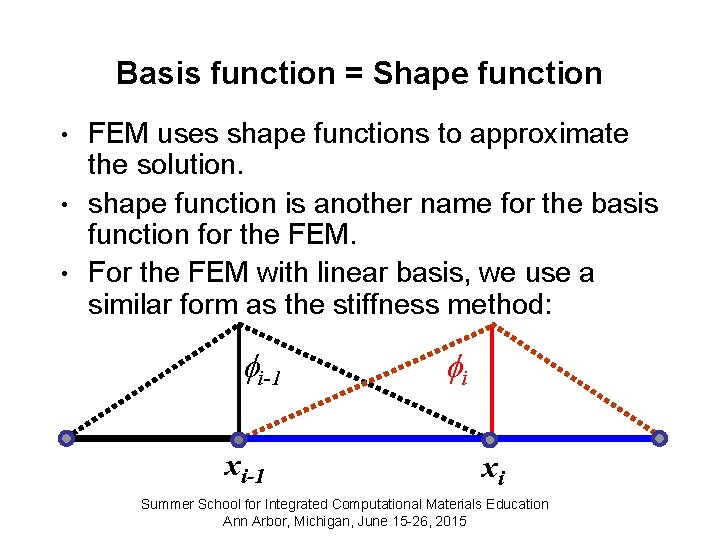
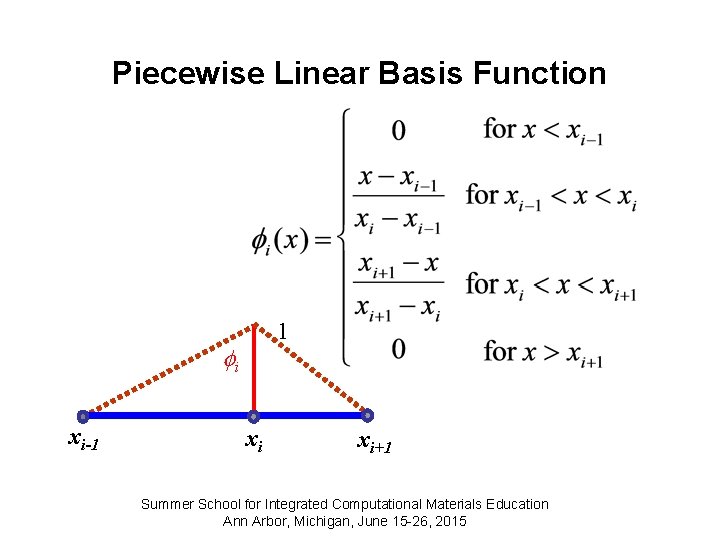
Basis function = Shape function • • • FEM uses shape functions to approximate the solution. shape function is another name for the basis function for the FEM. For the FEM with linear basis, we use a similar form as the stiffness method: i-1 xi-1 i xi Summer School for Integrated Computational Materials Education Ann Arbor, Michigan, June 15 -26, 2015

Piecewise Linear Basis Function 1 i xi-1 xi xi+1 Summer School for Integrated Computational Materials Education Ann Arbor, Michigan, June 15 -26, 2015

Derivatives of the Piecewise Linear Basis Function Summer School for Integrated Computational Materials Education Ann Arbor, Michigan, June 15 -26, 2015

Residual • Take the model diffusion equation, and move the source term to the left hand side: • Let be the estimate of the solution for u. Then the residual is given by • For an exact solution, = 0 for all x. Summer School for Integrated Computational Materials Education Ann Arbor, Michigan, June 15 -26, 2015

Method of Minimal Weighted Residual • • How do we evaluate how close the approximate solution is to the true solution? Let the ith weight function, wi(x), to be nonzero only on two consecutive elements around the node i. (This is 1 often the same as the basis function. ) i • Weighted residual to be minimized: xi-1 • The weighted residual becomes algebraic once the integral is performed. Summer School for Integrated Computational Materials Education Ann Arbor, Michigan, June 15 -26, 2015 xi xi+1

General Summary (1) • • Solution is approximated by We need to determine ai The condition for determining ai is to reduce the error. The error (residual) is determined by considering how the value of a different diff. eq. is when the approximate solution is substituted for the solution. Summer School for Integrated Computational Materials Education Ann Arbor, Michigan, June 15 -26, 2015

General Summary (2) • • • In FEM, the basis functions i are the shape functions. The residual can be calculated in various ways. We will focus on the method of weighted residual. In particular, when the weight functions are identical to the basis functions, the method is called the Galerkin method. Summer School for Integrated Computational Materials Education Ann Arbor, Michigan, June 15 -26, 2015

Steps in MWR FEM 1. 2. 3. 4. 5. 6. 7. 8. Discretize and Select Element Type Select a Solution Function Select a Set of Basis Functions Derive Local “Stiffness” Matrix and Equations Assemble Equations and Introduce B. C. ’s Solve for the Unknown Coefficients Rebuild the Solution from the Coefficients Interpret the Results Summer School for Integrated Computational Materials Education Ann Arbor, Michigan, June 15 -26, 2015