Integrated Computational Materials Engineering Education Calculation of Equation















- Slides: 23

Integrated Computational Materials Engineering Education Calculation of Equation of State Using Density Functional Theory Mark Asta 1, Katsuyo Thornton 2, and Larry Aagesen 3 1 Department of Materials Science and Engineering, University of California, Berkeley 2 Department of Materials Science and Engineering, University of Michigan, Ann Arbor 3 Idaho National Laboratory DFT Module Review, The 5 th Summer School for Integrated Computational Materials Education

Purposes of Density Functional Theory Module • Understand fundamentals of Density Functional Theory (DFT) • Apply DFT to calculate: – Equilibrium lattice constant – Bulk Modulus – Components of elastic constant tensor • Understand how to check for convergence of results DFT Module Review, The 5 th Summer School for Integrated Computational Materials Education

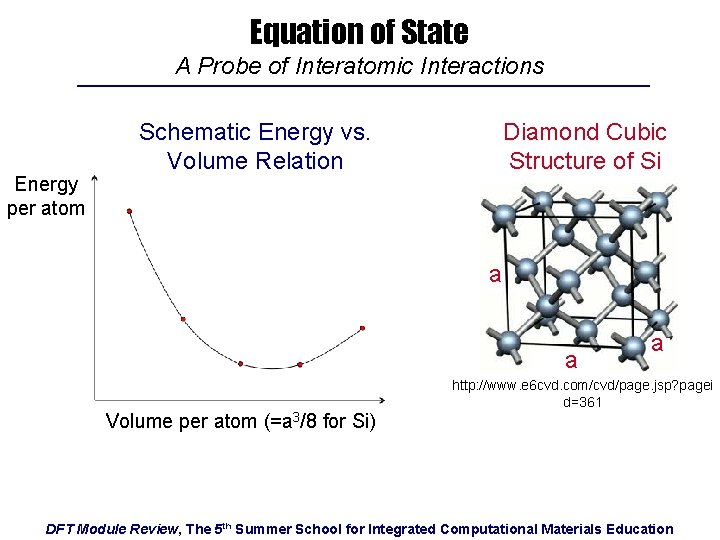
Equation of State A Probe of Interatomic Interactions Energy per atom Schematic Energy vs. Volume Relation Diamond Cubic Structure of Si a a Volume per atom (=a 3/8 for Si) a http: //www. e 6 cvd. com/cvd/page. jsp? pagei d=361 DFT Module Review, The 5 th Summer School for Integrated Computational Materials Education

Equation of State What Properties Can we Learn from It? Pressure versus Volume Relation Given E(V) one can compute P(V) by taking derivative Recall 1 st Law of Thermo: d. E = T d. S - P d. V and consider T = 0 K Equilibrium Volume (or Lattice Constant) Volume corresponding to zero pressure = Volume where slope of E(V) is zero ≈ Volume measured experimentally at P = 1 atm Bulk Modulus B related to curvature of E(V) Function DFT Module Review, The 5 th Summer School for Integrated Computational Materials Education

Generalize to Non-Hydrostatic Deformation Example of Uniaxial Deformation Lz Lz(1+e) Ly Lx Definition of Deformation In Terms of Strain: (All other strains are zero) DFT Module Review, The 5 th Summer School for Integrated Computational Materials Education

Linear-Elasticity for Single Crystals General form of Hook’s Law (Linear Elasticity): Stress Tensor Elastic Constant Tensor Strain Tensor Voigt Notation: 11 → 1, 22 → 2, 33 → 3, 23 → 4, 13 → 5, 12 → 6 Elastic Energy: In example from previous slide: (All other strains are zero) Note: for cubic crystal C 11=C 22=C 33, C 12=C 13=C 23 DFT Module Review, The 5 th Summer School for Integrated Computational Materials Education

Equation of State How to Calculate from Density Functional Theory Formulation: for a given arrangement of nuclei defined by the lattice constant, crystal structure, and non-hydrostatic strains, compute the total energy corresponding to the optimal arrangement of the electron density Theoretical Framework: Quantum mechanical calculation of energy of electrons and nuclei interacting through Coulomb potential Practical Implementation: Density functional theory DFT Module Review, The 5 th Summer School for Integrated Computational Materials Education

Total Energy in Density Functional Theory Electron Density Electron Wavefunctions Potential Electrons Feel from Nuclei Exchange-Correlation Energy Form depends on whether you use Local Density Approximation (LDA) or Generalized Gradient Approximation (GGA) DFT Module Review, The 5 th Summer School for Integrated Computational Materials Education

Kohn-Sham Equations Schrödinger Equation for Electron Wavefunctions Exchange-Correlation Potential Electron Density Note: fi depends on n(r) which depends on fi Solution of Kohn-Sham equations must be done iteratively DFT Module Review, The 5 th Summer School for Integrated Computational Materials Education

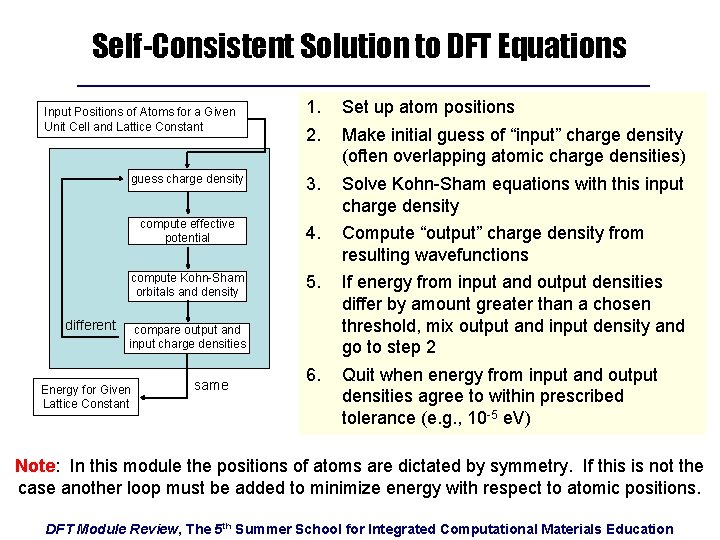
Self-Consistent Solution to DFT Equations 1. 2. Set up atom positions guess charge density 3. Solve Kohn-Sham equations with this input charge density compute effective potential 4. Compute “output” charge density from resulting wavefunctions compute Kohn-Sham orbitals and density 5. If energy from input and output densities differ by amount greater than a chosen threshold, mix output and input density and go to step 2 6. Quit when energy from input and output densities agree to within prescribed tolerance (e. g. , 10 -5 e. V) Input Positions of Atoms for a Given Unit Cell and Lattice Constant different compare output and input charge densities Energy for Given Lattice Constant same Make initial guess of “input” charge density (often overlapping atomic charge densities) Note: In this module the positions of atoms are dictated by symmetry. If this is not the case another loop must be added to minimize energy with respect to atomic positions. DFT Module Review, The 5 th Summer School for Integrated Computational Materials Education

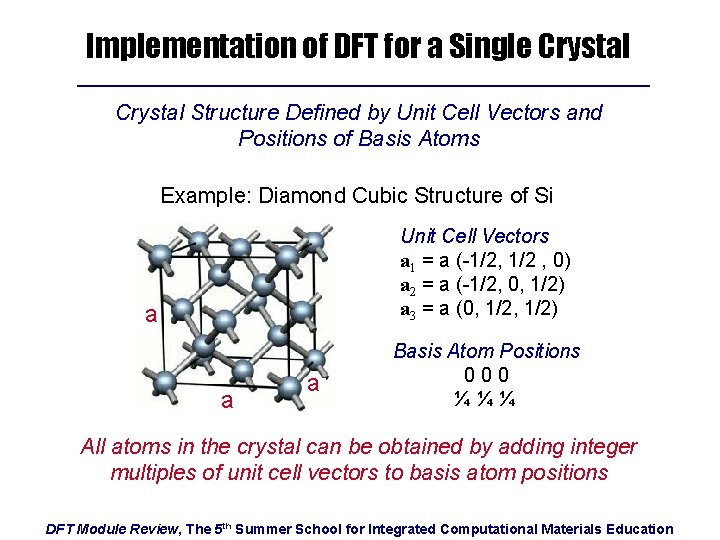
Implementation of DFT for a Single Crystal Structure Defined by Unit Cell Vectors and Positions of Basis Atoms Example: Diamond Cubic Structure of Si Unit Cell Vectors a 1 = a (-1/2, 1/2 , 0) a 2 = a (-1/2, 0, 1/2) a 3 = a (0, 1/2) a a a Basis Atom Positions 000 ¼¼¼ All atoms in the crystal can be obtained by adding integer multiples of unit cell vectors to basis atom positions DFT Module Review, The 5 th Summer School for Integrated Computational Materials Education

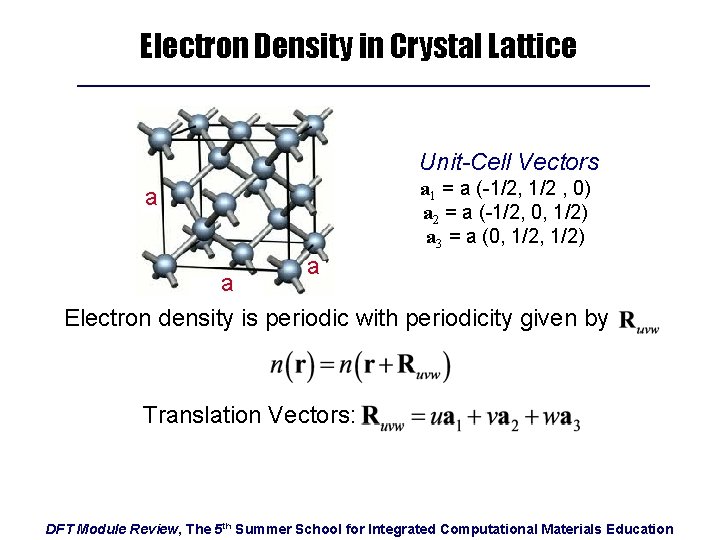
Electron Density in Crystal Lattice Unit-Cell Vectors a 1 = a (-1/2, 1/2 , 0) a 2 = a (-1/2, 0, 1/2) a 3 = a (0, 1/2) a a a Electron density is periodic with periodicity given by Translation Vectors: DFT Module Review, The 5 th Summer School for Integrated Computational Materials Education

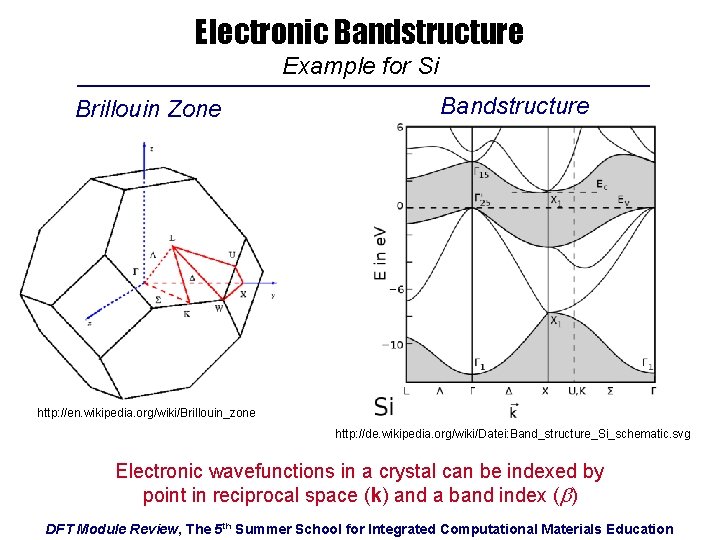
Electronic Bandstructure Example for Si Brillouin Zone Bandstructure http: //en. wikipedia. org/wiki/Brillouin_zone http: //de. wikipedia. org/wiki/Datei: Band_structure_Si_schematic. svg Electronic wavefunctions in a crystal can be indexed by point in reciprocal space (k) and a band index (b) DFT Module Review, The 5 th Summer School for Integrated Computational Materials Education

Why? Wavefunctions in a Crystal Obey Bloch’s Theorem For a given band b Where is periodic in real space: Translation Vectors: The envelope function represents delocalized distribution of electron density DFT Module Review, The 5 th Summer School for Integrated Computational Materials Education

Representation of Electron Density Integral over k-points in first Brillouin zone In practice the integral over the Brillouin zone is replaced with a sum over a finite number of k-points (Nkpt) Band occupation (e. g. , the Fermi function) One parameter that needs to be checked for numerical convergence is number of k-points DFT Module Review, The 5 th Summer School for Integrated Computational Materials Education

Representation of Wavefunctions Fourier-Expansion as Series of Plane Waves For a given band: Recall that is periodic in real space: can be written as a 3 D Fourier Series: where the are primitive reciprocal lattice vectors DFT Module Review, The 5 th Summer School for Integrated Computational Materials Education

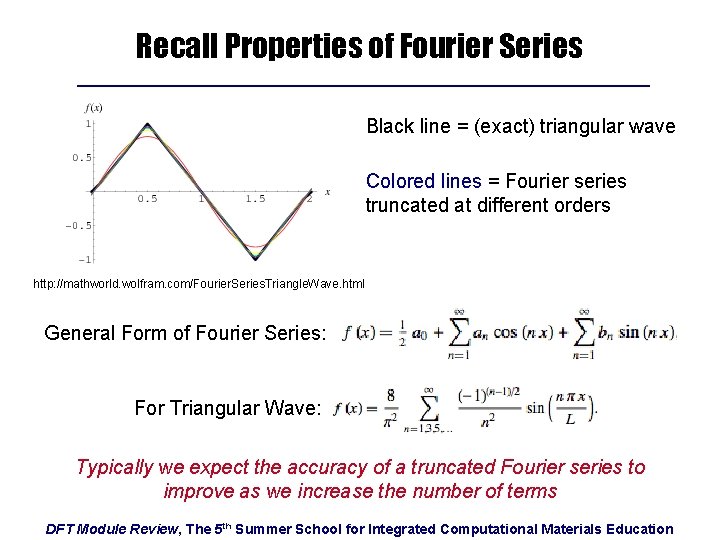
Recall Properties of Fourier Series Black line = (exact) triangular wave Colored lines = Fourier series truncated at different orders http: //mathworld. wolfram. com/Fourier. Series. Triangle. Wave. html General Form of Fourier Series: For Triangular Wave: Typically we expect the accuracy of a truncated Fourier series to improve as we increase the number of terms DFT Module Review, The 5 th Summer School for Integrated Computational Materials Education

Representation of Wavefunctions Plane-Wave Basis Set For a given band Use Fourier Expansion In practice the Fourier series is truncated to include all G for which: Another parameter that needs to be checked for convergence is the “plane-wave cutoff energy” Ecut DFT Module Review, The 5 th Summer School for Integrated Computational Materials Education

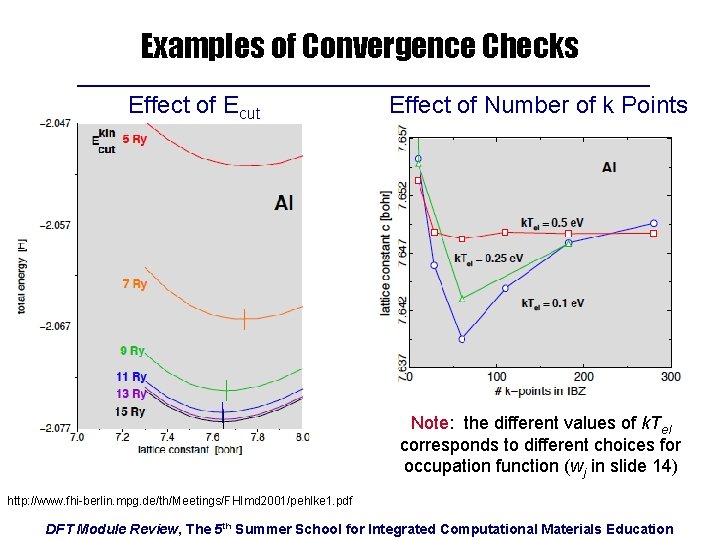
Examples of Convergence Checks Effect of Ecut Effect of Number of k Points Note: the different values of k. Tel corresponds to different choices for occupation function (wj in slide 14) http: //www. fhi-berlin. mpg. de/th/Meetings/FHImd 2001/pehlke 1. pdf DFT Module Review, The 5 th Summer School for Integrated Computational Materials Education

DFT Module • Problem 1: Calculate equilibrium volume and bulk modulus of diamond cubic Si using Quantum Espresso on Nanohub (http: //nanohub. org/) o Outcome 1: Understand effect of numerical parameters on calculated results by testing convergence with respect to number of k-points and plane-wave cutoff o Outcome 2: Understand the effect of theoretical model for exchange-correlation potential on the accuracy of the calculations by comparing results from Local Density Approximation (LDA) and Generalized Gradient Approximation (GGA) with experimental measurements DFT Module Review, The 5 th Summer School for Integrated Computational Materials Education

DFT Module • Problem 2: Calculate the single-crystal elastic constants C 11 and C 12 o Outcome 1: Understand how to impose homogeneous elastic deformations in a DFT calculation o Outcome 2: Understand the effect of theoretical model for exchange-correlation potential on the accuracy of the calculations by comparing results from Local Density Approximation (LDA) and Generalized Gradient Approximation (GGA) with experimental measurements DFT Module Review, The 5 th Summer School for Integrated Computational Materials Education

DFT Module • For problem 1 you will make use of the unit cell for diamond-cubic Si shown below. You will vary only the lattice constant a. Unit Cell Vectors a 1 = a (-1/2, 1/2 , 0) a 2 = a (-1/2, 0, 1/2) a 3 = a (0, 1/2) a a a Basis Atom Positions (Fractional Coordinates) 000 ¼¼¼ DFT Module Review, The 5 th Summer School for Integrated Computational Materials Education

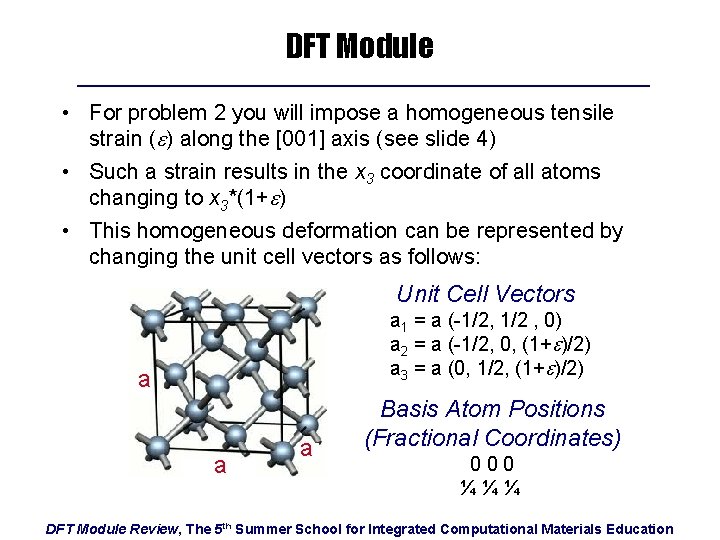
DFT Module • For problem 2 you will impose a homogeneous tensile strain (e) along the [001] axis (see slide 4) • Such a strain results in the x 3 coordinate of all atoms changing to x 3*(1+e) • This homogeneous deformation can be represented by changing the unit cell vectors as follows: Unit Cell Vectors a 1 = a (-1/2, 1/2 , 0) a 2 = a (-1/2, 0, (1+e)/2) a 3 = a (0, 1/2, (1+e)/2) a a a Basis Atom Positions (Fractional Coordinates) 000 ¼¼¼ DFT Module Review, The 5 th Summer School for Integrated Computational Materials Education
 Integrated computational materials engineering
Integrated computational materials engineering Integrated computational materials engineering
Integrated computational materials engineering Tu bergakademie freiberg computational materials science
Tu bergakademie freiberg computational materials science Purdue computational science and engineering
Purdue computational science and engineering Computational engineering and physical modeling
Computational engineering and physical modeling Natural materials and man made materials
Natural materials and man made materials Material that useful and harmful
Material that useful and harmful Man made materials
Man made materials Adapting and adopting materials
Adapting and adopting materials Direct materials budget with multiple materials
Direct materials budget with multiple materials Integrated engineering meaning
Integrated engineering meaning Integrated design project civil engineering
Integrated design project civil engineering Integrated engineering management system
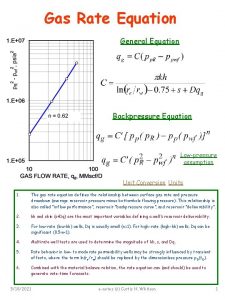
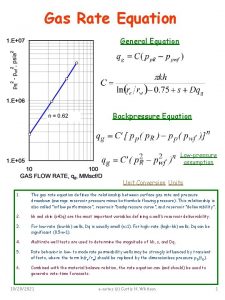
Integrated engineering management system Integrated rate equation
Integrated rate equation Integrated holistic education system
Integrated holistic education system Integrated education
Integrated education Summary sheet of iqms scores
Summary sheet of iqms scores Manufacturing processes for engineering materials 5th
Manufacturing processes for engineering materials 5th Types of engineering materials
Types of engineering materials What is the engineering materials
What is the engineering materials Optical properties of engineering materials
Optical properties of engineering materials Hot materials
Hot materials What is the engineering materials
What is the engineering materials Engineering materials
Engineering materials