SUDUT SUDUT PADA LINGKARAN Materi Sudut pusat dan

SUDUT –SUDUT PADA LINGKARAN Materi : • Sudut pusat dan sudut keliling • Sudut antara dua tali busur yang berpotongan di luar lingkaran • Garis singgung lingkaran

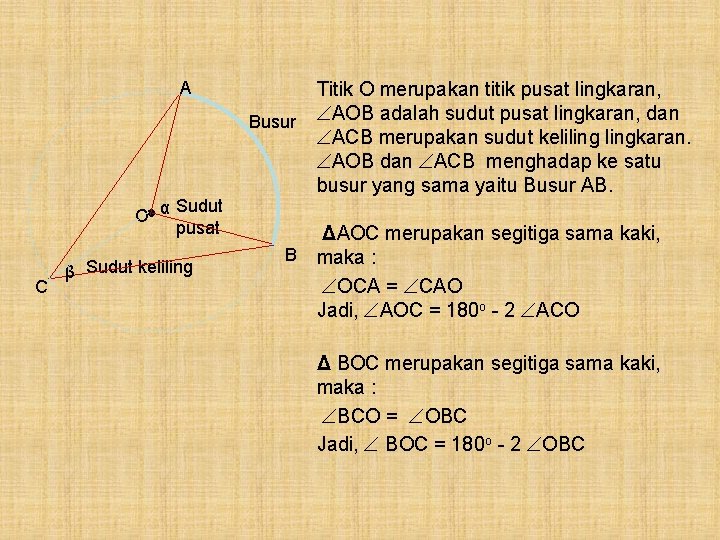
A Busur Sudut O● α pusat C β Sudut keliling Titik O merupakan titik pusat lingkaran, AOB adalah sudut pusat lingkaran, dan ACB merupakan sudut kelilingkaran. AOB dan ACB menghadap ke satu busur yang sama yaitu Busur AB. ΔAOC merupakan segitiga sama kaki, B maka : OCA = CAO Jadi, AOC = 180 o - 2 ACO Δ BOC merupakan segitiga sama kaki, maka : BCO = OBC Jadi, BOC = 180 o - 2 OBC

Perhatikan Sudut Pusat AOB = 360 o – ( AOC + BOC) = 360 o – (180 o – 2 ACO+ 180 o – 2 OBC) = 360 o – (360 o – 2 ACO+ 180 o – 2 OBC) = 2( ACO+ OBC) = 2 ACB Kesimpulan, Bahwa jika sudut pusat lingkaran dan sudut kelilingkaran menghadap ke Busur yang sama, maka besar Sudut Pusat Lingkaran adalah 2 kali besar sudut keliling Lingkaran

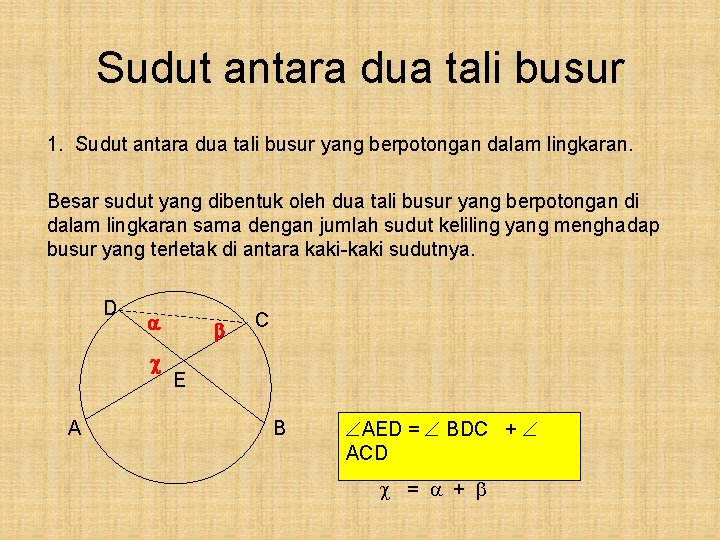
Sudut antara dua tali busur 1. Sudut antara dua tali busur yang berpotongan dalam lingkaran. Besar sudut yang dibentuk oleh dua tali busur yang berpotongan di dalam lingkaran sama dengan jumlah sudut keliling yang menghadap busur yang terletak di antara kaki-kaki sudutnya. D A C E B AED = BDC + ACD = +

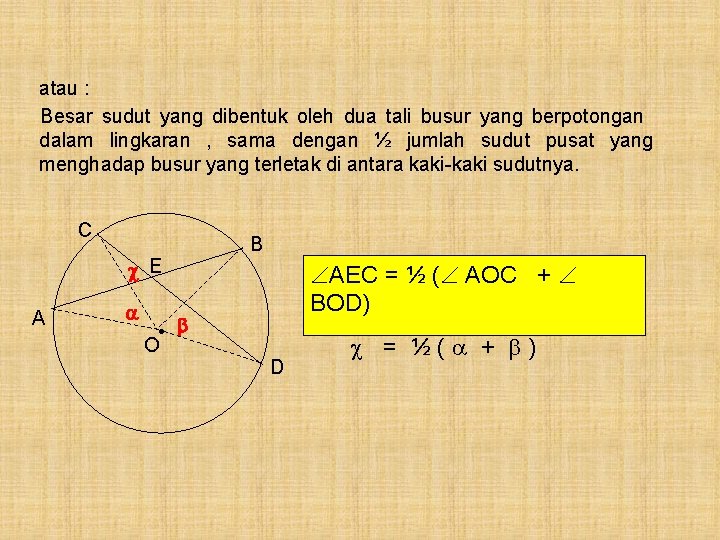
atau : Besar sudut yang dibentuk oleh dua tali busur yang berpotongan dalam lingkaran , sama dengan ½ jumlah sudut pusat yang menghadap busur yang terletak di antara kaki-kaki sudutnya. C E A • O B AEC = ½ ( AOC + BOD) D = ½( + )

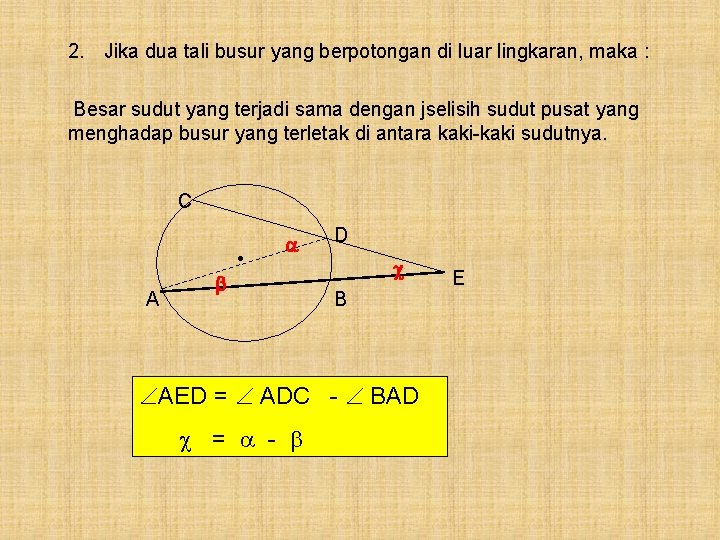
2. Jika dua tali busur yang berpotongan di luar lingkaran, maka : Besar sudut yang terjadi sama dengan jselisih sudut pusat yang menghadap busur yang terletak di antara kaki-kaki sudutnya. C • A D B AED = ADC - BAD = - E

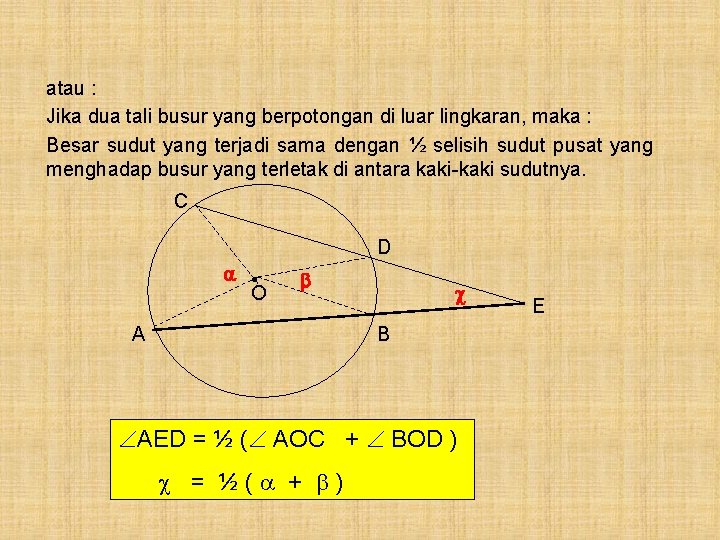
atau : Jika dua tali busur yang berpotongan di luar lingkaran, maka : Besar sudut yang terjadi sama dengan ½ selisih sudut pusat yang menghadap busur yang terletak di antara kaki-kaki sudutnya. C D • O A B AED = ½ ( AOC + BOD ) = ½( + ) E

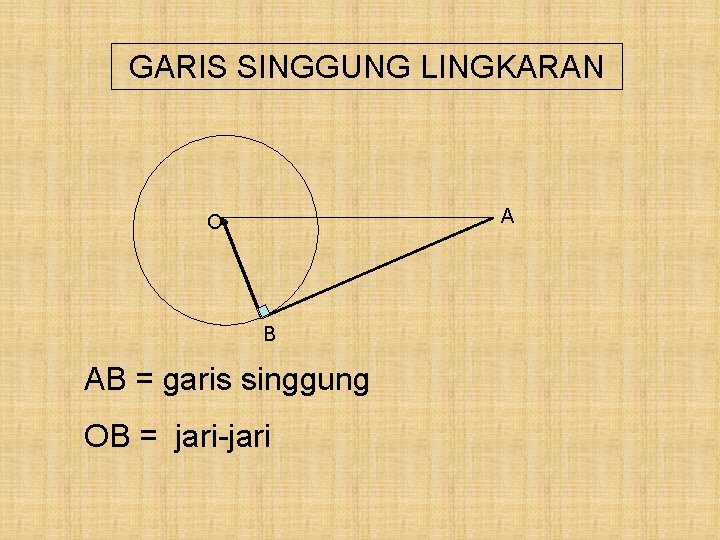
GARIS SINGGUNG LINGKARAN A O • B AB = garis singgung OB = jari-jari

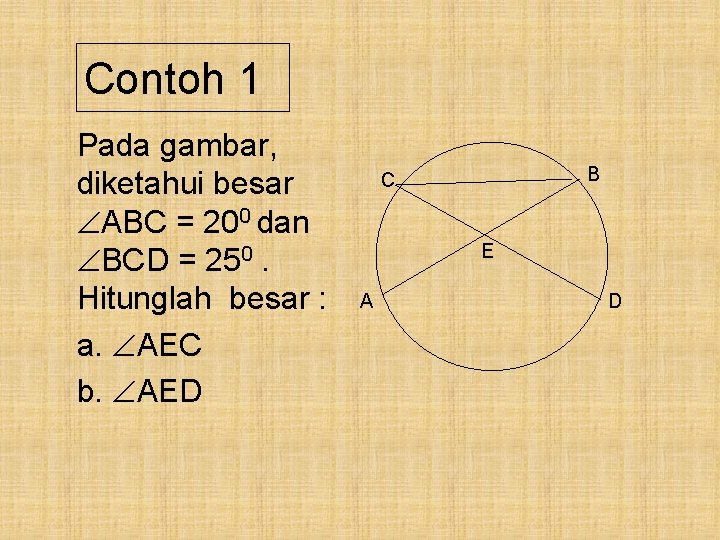
Contoh 1 Pada gambar, diketahui besar ABC = 200 dan BCD = 250. Hitunglah besar : a. AEC b. AED B C E A D

Pembahasan : ABC = 200 BCD = 250 a. AEC = ABC + BCD = 200 + 250 = 450 b. AED = 1800 - AEC = 1800 - 450 = 1350

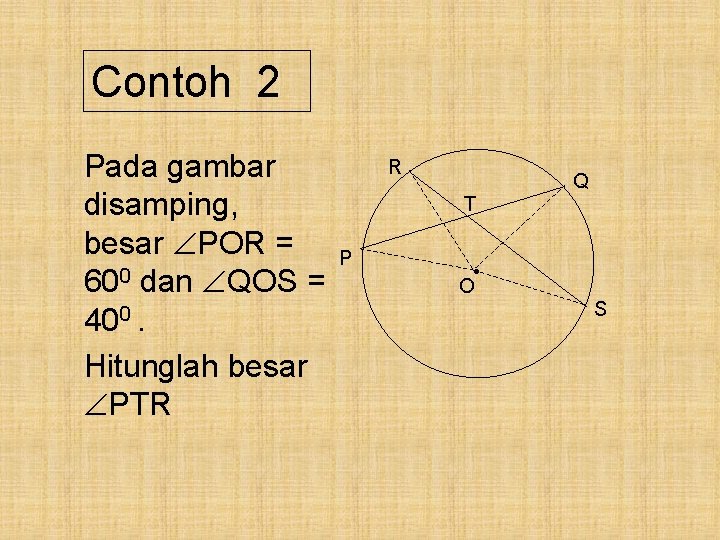
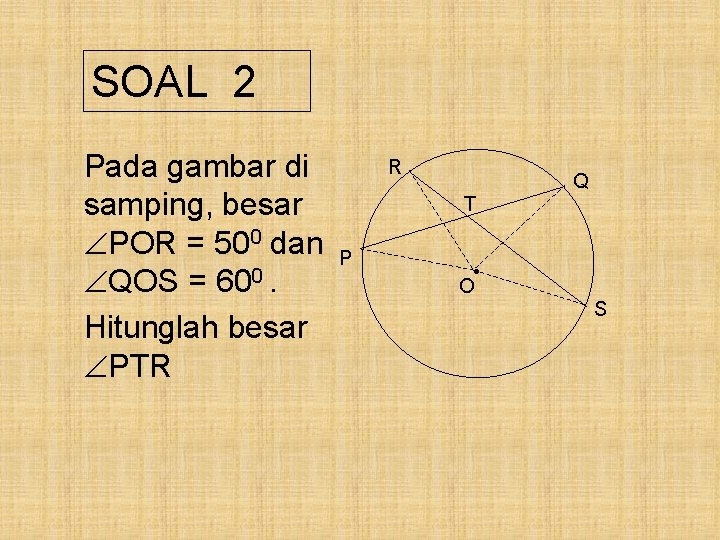
Contoh 2 Pada gambar disamping, besar POR = 600 dan QOS = 400. Hitunglah besar PTR R Q T P • O S

Pembahasan : POR = 600 QOS = 400 a. PTR = ½ ( POR + QOS) = ½ (600 + 400 ) = ½ x 1000 = 500 Jadi, besar PTR = 500

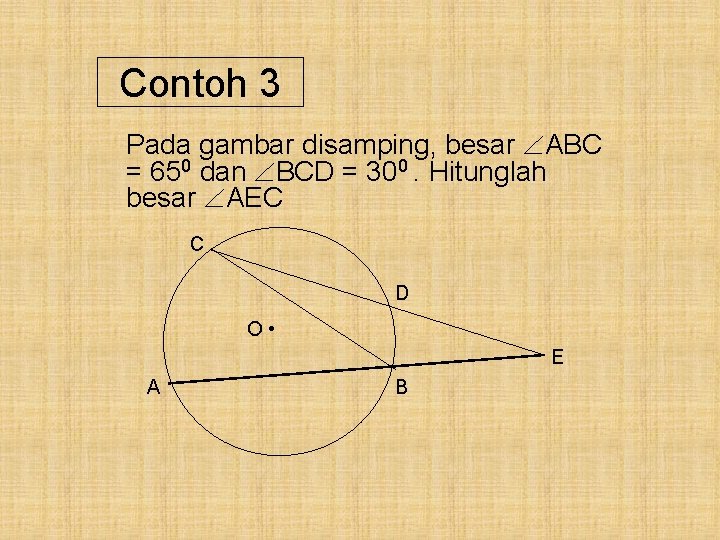
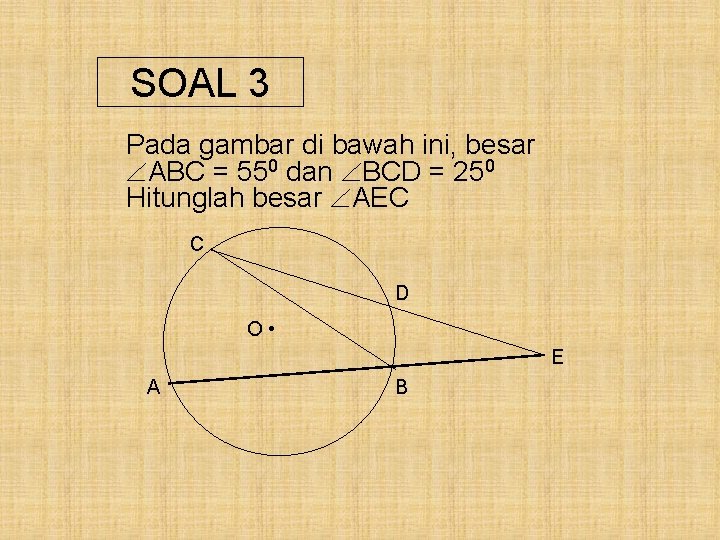
Contoh 3 Pada gambar disamping, besar ABC = 650 dan BCD = 300. Hitunglah besar AEC C D O • E A B

Pembahasan : ABC = 650 BCD = 300 AEC = ABC - BCD = 650 - 350 = 250 Jadi, besar AEC = 250

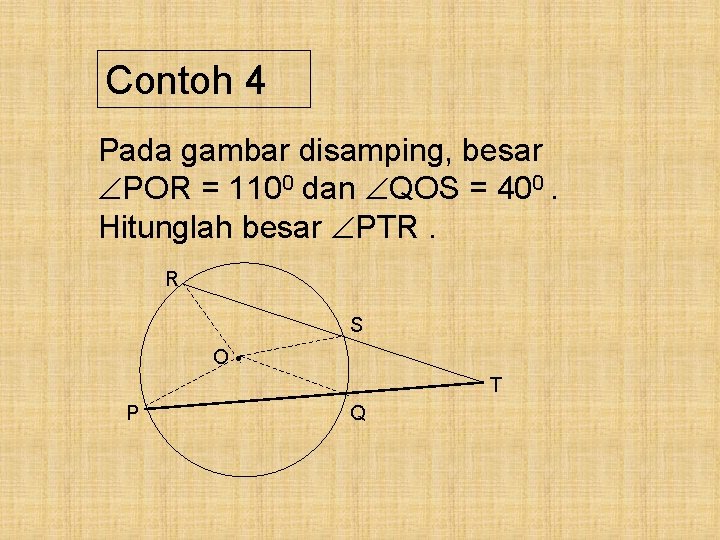
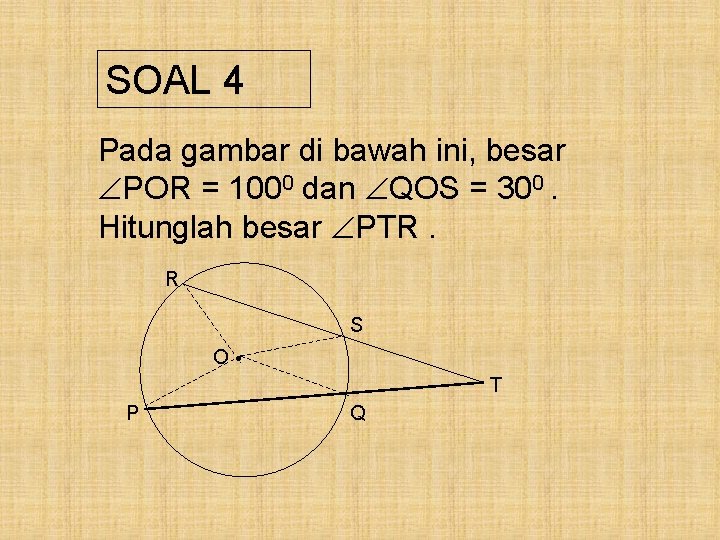
Contoh 4 Pada gambar disamping, besar POR = 1100 dan QOS = 400. Hitunglah besar PTR. R S O • T P Q

Pembahasan : POR = 1100 QOS = 400 PTR = ½ ( POR - QOS) = ½ ( 1100 - 400 ) = 350 Jadi, besar PTR = 350

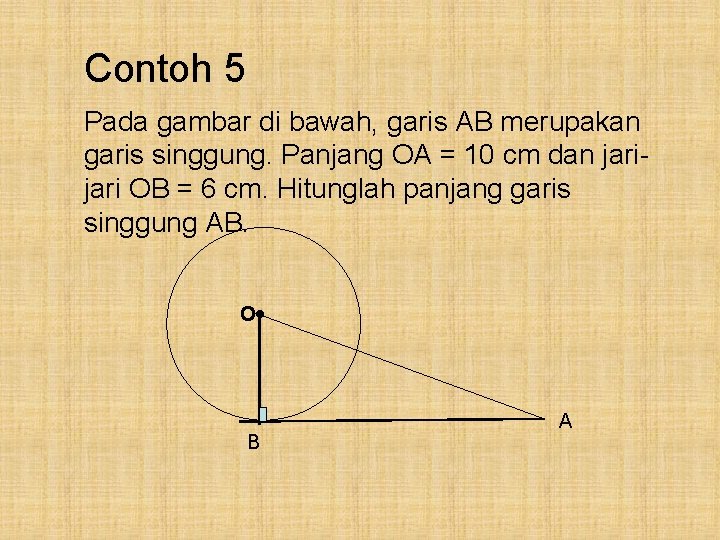
Contoh 5 Pada gambar di bawah, garis AB merupakan garis singgung. Panjang OA = 10 cm dan jari OB = 6 cm. Hitunglah panjang garis singgung AB. • O B A

Pembahasan : Perhatikan Δ OAB siku-siku di titik B AB 2 = OA 2 - OB 2 = 102 - 62 = 100 - 36 = 64 AB = √ 64 = 8 cm. Jadi, panjang garis singgung AB = 8 cm.

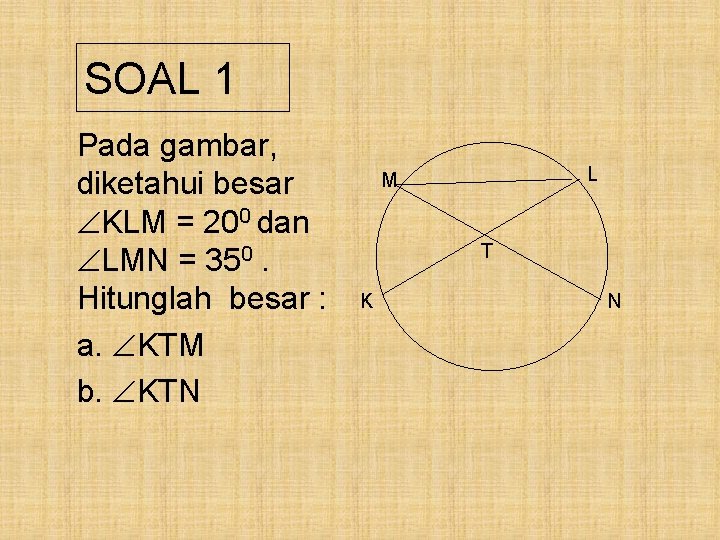
SOAL 1 Pada gambar, diketahui besar KLM = 200 dan LMN = 350. Hitunglah besar : a. KTM b. KTN L M T K N

Pembahasan : KLM = 200 LMN = 350 a. KTM = KLM + LMN = 200 + 350 = 550 b. KTN = 1800 - KTM = 1800 - 550 = 1250

SOAL 2 Pada gambar di samping, besar POR = 500 dan QOS = 600. Hitunglah besar PTR R Q T P • O S

Pembahasan : POR = 500 QOS = 600 a. PTR = ½ ( POR + QOS) = ½ (500 + 600 ) = ½ x 1100 = 550 Jadi, besar PTR = 550

SOAL 3 Pada gambar di bawah ini, besar ABC = 550 dan BCD = 250 Hitunglah besar AEC C D O • E A B

Pembahasan : ABC = 550 BCD = 250 AEC = ABC - BCD = 550 - 250 = 300 Jadi, besar AEC = 300

SOAL 4 Pada gambar di bawah ini, besar POR = 1000 dan QOS = 300. Hitunglah besar PTR. R S O • T P Q

Pembahasan : POR = 1000 QOS = 300 PTR = ½ ( POR - QOS) = ½ ( 1000 - 300 ) = 350 Jadi, besar PTR = 350

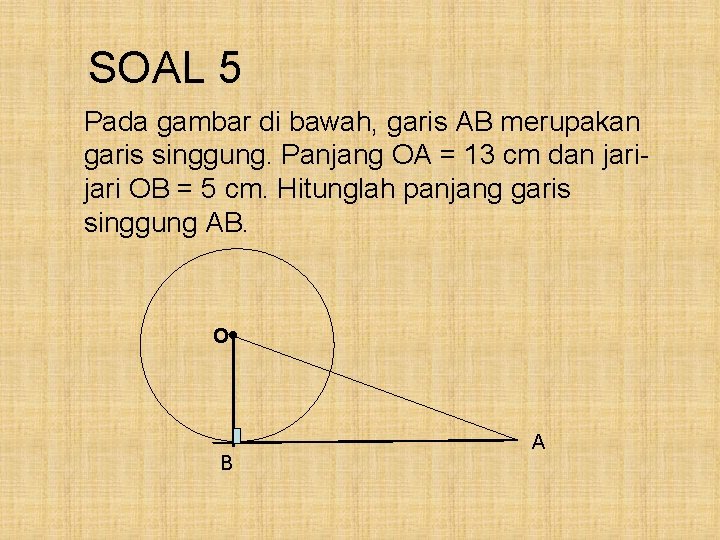
SOAL 5 Pada gambar di bawah, garis AB merupakan garis singgung. Panjang OA = 13 cm dan jari OB = 5 cm. Hitunglah panjang garis singgung AB. • O B A

Pembahasan : Perhatikan Δ OAB siku-siku di titik B AB 2 = OA 2 - OB 2 = 132 - 52 = 169 - 25 = 144 AB = √ 144 = 12 cm. Jadi, panjang garis singgung AB = 12 cm.

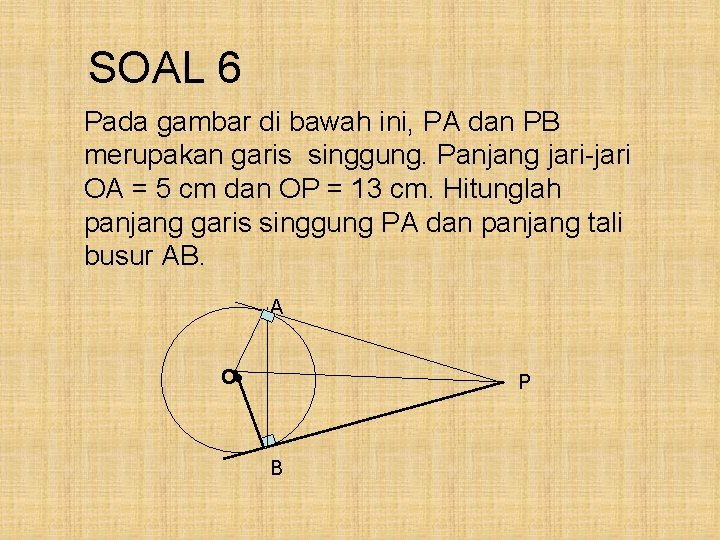
SOAL 6 Pada gambar di bawah ini, PA dan PB merupakan garis singgung. Panjang jari-jari OA = 5 cm dan OP = 13 cm. Hitunglah panjang garis singgung PA dan panjang tali busur AB. A • O P B

Pembahasan : OA = 5 cm dan OP = 13 cm. ∆ AOP siku-siku di titik A PA 2 = OP 2 - OA 2 = 132 - 52 = 169 – 25 = 144 PA = √ 144 = 12 Jadi, panjang garis singgung PA= 12 cm.

Luas layang-layang OAPB L. OAPB = ½ x OP x AB 2( ½ x 12 x 5) = ½ x 13 x AB 120 = 13 AB AB = 120 : 13 = 9, 23 Jadi, panjang tali busur AB = 9, 23 cm.

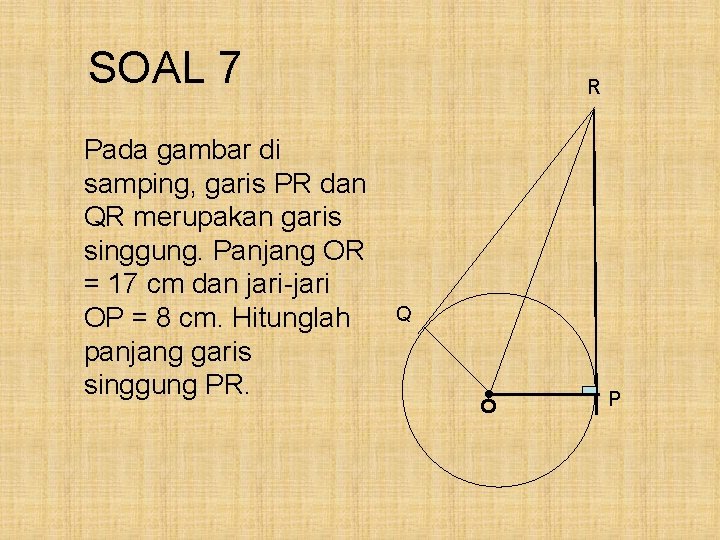
SOAL 7 • Q O Pada gambar di samping, garis PR dan QR merupakan garis singgung. Panjang OR = 17 cm dan jari-jari OP = 8 cm. Hitunglah panjang garis singgung PR. R P

Pembahasan : OP = 8 cm dan OR = 17 cm. ∆ POR siku-siku di titik P PR 2 = OR 2 - OP 2 = 172 - 82 = 289 – 64 = 225 PA = √ 225 = 15 Jadi, panjang garis singgung PR= 15 cm.