Standard Kompetensi Indikator Definisi Lingkaran LINGKARAN lingkaran Pusat

Standard Kompetensi Indikator Definisi Lingkaran LINGKARAN lingkaran Pusat ( 0, 0 ) LINGKARAN PUSAT ( a, b ) CONTOH Persamaan Garis Singgung Lingkaran SOAL-SOAL LINGKARAN

lingkaran Ling P(0, 0) Contoh 1: NO : 2 Ling P(a, b) Contoh 2 : LINGKARAN BY TIM MATEMATIKA SMKN 11 SURABAYA kembali

Lingkaran adalah …. Tempat kedudukan titik-titik yang berjarak sama ( jari –jari ) terhadap titik tertentu ( pusat ) KEMBALI

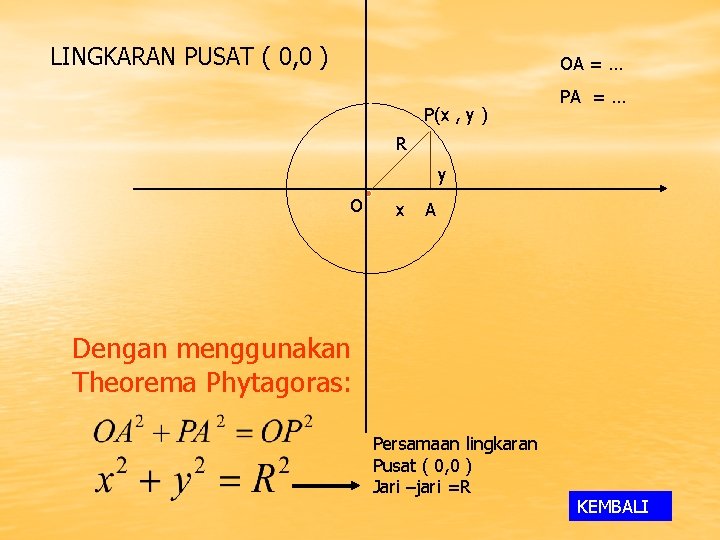
LINGKARAN PUSAT ( 0, 0 ) OA = … P(x , y ) PA = … R y O x A Dengan menggunakan Theorema Phytagoras: Persamaan lingkaran Pusat ( 0, 0 ) Jari –jari =R KEMBALI

Contoh: 1. Tentukan persama an lingkaran pusat ( 0, 0 ) jari-jari 5 Jawab : 1.

2. Tentukan persama an lingkaran dengan pusat ( 0, 0) melalui ( 3, 4 ) Pusat ( 0, 0 ) Jari-jari =OP 2. Jawab P (3, 4) O KEMBALI

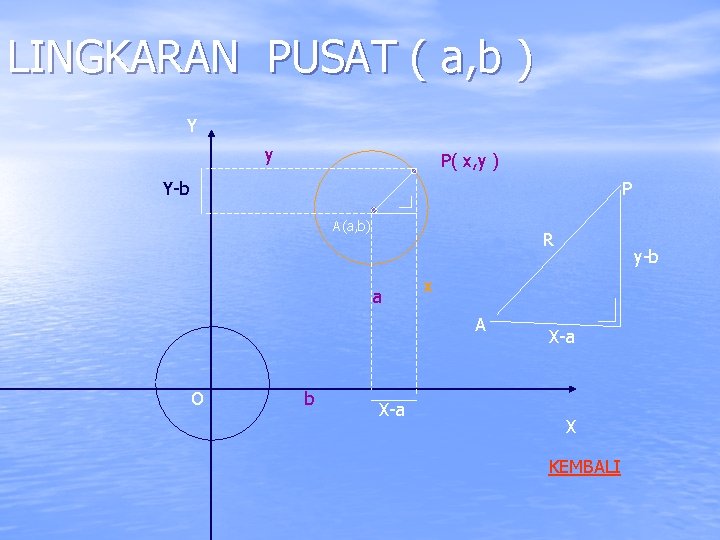
LINGKARAN PUSAT ( a, b ) Y y P( x, y ) Y-b P A(a, b) R a x A O b X-a y-b X-a X KEMBALI

Lihat segitiga siku-siku yang diperbesar Dengan mengguanakan theorema Phytagoras Persamaan lingkaran Pusat ( a, b ) jari-jari R KEMBALI

Contoh : 1. Tentukan pusat dan jari-jari : Jawab: 1. Pusat ( 2, -3 ) Jari-jari 8 2. Tentukan persama an lingkaran jika : a. Pusat ( -1, 2 ) dan jari-jari 5 KEMBALI

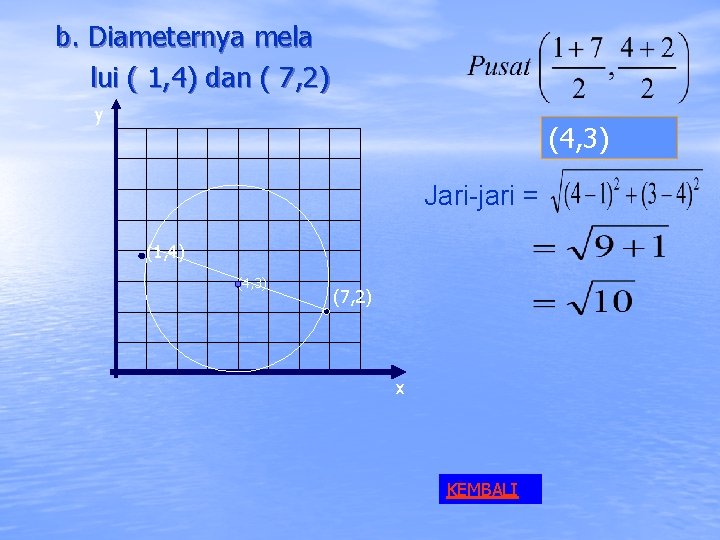
b. Diameternya mela lui ( 1, 4) dan ( 7, 2) y (4, 3) Jari-jari = (1, 4) (4, 3) (7, 2) x KEMBALI

Soal –Soal Latihan : 1. Tentukan pusat dan jari-jari a. b. c. 2. Tentukan persamaan lingkaran jika diketahui : a. Pusat ( 0, 0) R =7 b. Pusat ( 0, 0 ) mela ( 5, 12 ) c. Pusat ( 3, -1 ) R = 2 d. Pusat ( 1, 7 ) melalui ( 2, -6 ) e. Diameternya melalui ( 3, 7 ) dan ( -5, 3 ) KEMBALI

STANDART KOMPETENSI: 1. Menggunakan aturan statistika, kaidah pencacahan, dan sifat-sifat peluang dalam pemecahan masalah KOMPETENSI DASAR : Menyusun persamaan lingkaran yang memenuhi persyaratan Yang ditentukan KEMBALI

INDIKATOR : 1. Merumuskan persamaan lingkaran berpusat di ( 0, 0 ) dan ( a, b ) 2. Menentukan pusat dan jari-jari lingkaran yang persamaannya diketahui 3. Menentukan persamaan lingkaran memenuhi kriteria tertentu KEMBALI

Standar Kompetensi Indikator Definisi Lingkaran LINGKARAN Linnkaran Pusat ( 0, 0 ) CONTOH Lingkaran Pusat ( a, b ) CONTOH Persamaan Garis Singgung Lingkaran SOAL-SOAL LINGKARAN