PERSAMAAN LINGKARAN PERSAMAAN LINGKARAN Persamaan Lingkaran Hal Isi

PERSAMAAN LINGKARAN

PERSAMAAN LINGKARAN

Persamaan Lingkaran Hal. : Isi dengan Judul Halaman Terkait Adaptif

Persamaan Lingkaran Hal. : Isi dengan Judul Halaman Terkait Adaptif

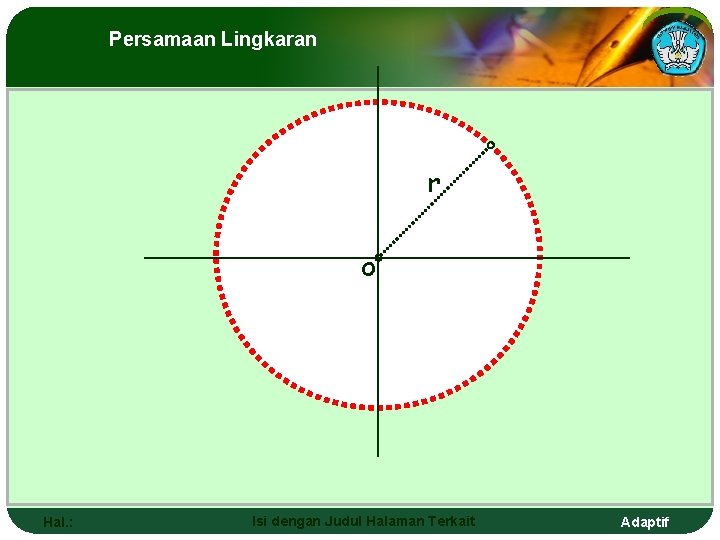
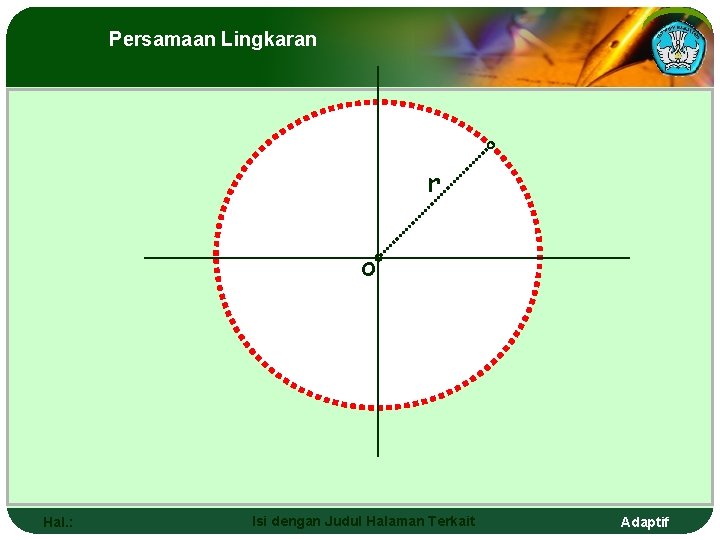
Persamaan lingkaran LINGKARAN DIDEFINISIKAN SEBAGAI HIMPUNAN TITIK YANG BERJARAK TETAP TERHADAP TITIK TERTENTU, DIMANA TITIK TERTENTU TERSEBUT DISEBUT SEBAGAI PUSAT LINGKARAN DAN JARAK YANG TETAP DISEBUT JARI - JARI Hal. : Isi dengan Judul Halaman Terkait Adaptif

Persamaan lingkaran CIRCLE IS DEFINED AS SET OF POINTS THAT WITH THE SAME DISTANCE TOWARDS A PARTICULAR REFERENCE POINT, AND IT IS MENTIONED AS CIRCLE CENTRAL AND THE SAME DISTANCE CALLED RADIUS Hal. : Isi dengan Judul Halaman Terkait Adaptif

Persamaan Lingkaran r o Hal. : Isi dengan Judul Halaman Terkait Adaptif

Persamaan Lingkaran r o Hal. : Isi dengan Judul Halaman Terkait Adaptif

Persamaan Lingkaran Berpusat di Titik O(0, 0) dan Berjari-jari r Persamaan Lingkaran Berpusat di Titik P(a, b) dan Berjari-jari r Hal. : Isi dengan Judul Halaman Terkait Adaptif

Persamaan Lingkaran The e. Equation of a Circle The equation of the circle with center of O(0, 0) and radius r The equation of the circle with center of P(a, b) and radius r Hal. : Isi dengan Judul Halaman Terkait Adaptif

Y r o T (x, y) OT 2 2 ( x 2 - x 1 ) + ( y 2 - y 1 ) = r X 2 ( x - 0) + ( y - 0) x Hal. : =r 2 +y Isi dengan Judul Halaman Terkait 2 = r 2 =r 2 Adaptif

Y r o T (x, y) OT 2 2 ( x 2 - x 1 ) + ( y 2 - y 1 ) = r X 2 ( x - 0) + ( y - 0) x Hal. : =r 2 +y Isi dengan Judul Halaman Terkait 2 = r 2 =r 2 Adaptif

Persamaan Lingkaran Hal. : Isi dengan Judul Halaman Terkait Adaptif

Persamaan Lingkaran Hal. : Isi dengan Judul Halaman Terkait Adaptif

Persamaan lingkaran Soal Latihan Tentukan persamaan lingkaran yang berpusat di titik O (0, 0) dan : a. berjari-jari 2 b. melalui titik (3, 4) Hal. : Isi dengan Judul Halaman Terkait Adaptif

Persamaan lingkaran Exercise Determine the circle equation that center to point O (0, 0) and : a. radius of 2 b. through the point (3, 4) Hal. : Isi dengan Judul Halaman Terkait Adaptif

Y PT = r 2 2 ( x 2 - x 1 ) + ( y 2 - y 1 ) = r r P (a, b ) O Hal. : T (x, y) X 2 2 ( x - a) + ( y - b) =r 2 2 2 (x-a) + (y-b) = r Isi dengan Judul Halaman Terkait Adaptif

Y PT = r 2 2 ( x 2 - x 1 ) + ( y 2 - y 1 ) = r r P (a, b ) O Hal. : T (x, y) X 2 2 ( x - a) + ( y - b) =r 2 2 2 (x-a) + (y-b) = r Isi dengan Judul Halaman Terkait Adaptif

Persamaan Lingkaran Hal. : Isi dengan Judul Halaman Terkait Adaptif

Persamaan Lingkaran Hal. : Isi dengan Judul Halaman Terkait Adaptif

Persamaan lingkaran Soal Latihan Tentukan persamaan lingkaran jika : a. Berpusat di titik P (3, 2) dan berjari-jari 4 b. Berpusat di titik Q (2, -1) dan melalui titik R(5, 3) Hal. : Isi dengan Judul Halaman Terkait Adaptif

Persamaan lingkaran Exercise Determine the circle equation if : a. Center to P (3, 2) and radius of 4 b. Center to point Q (2, -1) and through the point of R(5, 3) Hal. : Isi dengan Judul Halaman Terkait Adaptif

Hal. : Isi dengan Judul Halaman Terkait Adaptif

Hal. : Isi dengan Judul Halaman Terkait Adaptif

ELIPS Hal. : Isi dengan Judul Halaman Terkait Adaptif

ELLIPSE Hal. : Isi dengan Judul Halaman Terkait Adaptif

Elips Standar Kompetensi Menerapkan konsep irisan kerucut dalam memecahkan masalah. Kompetensi dasar: 3. Menerapkan konsep elips Indikator 1. Menjelaskan pengertian elips. 2. Menentukan unsur-unsur elips. 3. Menentukan persamaan elips 4. Melukis grafik persamaan ellips Hal. : Isi dengan Judul Halaman Terkait Adaptif

Ellipse Standard Competence Applying cone section concept in solving problem. Base Competence: 3. Applying ellipse concept Indicators 1. Explaining understanding of ellipse. 2. Determining ellipse terms. 3. Determining ellipse equation 4. Drawing graph of ellipse equation Hal. : Isi dengan Judul Halaman Terkait Adaptif

Elips Indikator 1. Menjelaskan pengertian elips. 2. Menentukan unsur-unsur elips. 3. Menentukan persamaan elips. 4. Melukis grafik persamaan elips. Hal. : Isi dengan Judul Halaman Terkait Adaptif

Ellipse Indicators 1. Explaining understanding of ellipse. 2. Determining ellipse terms. 3. Determining ellipse equation. 4. Drawing graph of ellipse equation. Hal. : Isi dengan Judul Halaman Terkait Adaptif

Elips Pengertian Elips adalah tempat kedudukan titik-titik pada bidang datar yang jumlah jaraknya terhadap dua titik tertentu yang diketahui adalah tetap (konstan). Hal. : Isi dengan Judul Halaman Terkait Adaptif

Ellipse Definition of Ellipse is position place of points on the flat surface which has total distance towards certain two points that is constant. Hal. : Isi dengan Judul Halaman Terkait Adaptif

Elips Perhatikan Gambar Elips Unsur-unsur elips D Unsur-unsur pada elips: (0, b) K B 1 (- c, 0) F 1 E T 2. b a A 1 1. F 1 dan F 2 disebut fokus. P (c, 0) F 2 B 2 L (0, -b) A 2 Jika T sembarang titik pada elips maka TF 1 + TF 2 = 2 a, F 1 F 2 = 2 c, dengan 2 a > 2 c. 3. 2. A 1 A 2 merupakan sumbu panjang (mayor)= 2 a. B 1 B 2 merupakan sumbu pendek (minor) = 2 b, karena itu a > b. Lanjut Hal. : Isi dengan Judul Halaman Terkait Adaptif

Ellipse See this ellipse picture Ellipse terms D The terms in ellipse: (0, b) K B 1 (- c, 0) F 1 E T 2. b a A 1 1. F 1 and F 2 called focus. P (c, 0) F 2 B 2 L A 2 If T is random point in ellipse then TF 1 + TF 2 = 2 a, F 1 F 2 = 2 c, and 2 a > 2 c. 3. 2. A 1 A 2 is long axis (mayor)= 2 a. B 1 B 2 is short axis (minor) = 2 b, that’s why a > b. (0, -b) continue Hal. : Isi dengan Judul Halaman Terkait Adaptif

Elips Lanjutan Elips 3. Latus Rectum yaitu segmen garis yang dibatasi elips, tegak lurus sumbu mayor dan melalui fokus (DE dan KL), panjang Latus Rectum DE = KL = 4. Titik pusat (P) yaitu titik potong sumbu mayor dengan sumbu minor. 5. Titik puncak elips yaitu titik A 1, A 2, B 1, B 2. Hal. : Isi dengan Judul Halaman Terkait Adaptif

Ellipse 3. Lotus Rectum is line segment that limits ellipse, upright straight to mayor axis through focus (DE and KL), length of Lotus Rectum DE = KL = 4. Center point (P) is intersection point toward mayor axis with minor axis. 5. Top point of ellipse is point A 1, A 2, B 1, B 2. Hal. : Isi dengan Judul Halaman Terkait Adaptif

Elips Persamaan Elips 1. Persamaan Elips yang berpusat di O(0, 0) Persamaan Elips : TF 1 + TF 2 = 2 a + = 2 a Mengkuadratkan ruas kiri dan kanan sehingga diperoleh …… (a 2 - c 2) x 2 + a 2 y 2 = a 2(a 2 -c 2). . . (i), jika titik T pada titik puncak pada sumbu minor (0, b) maka diperoleh …. b 2 =a 2 – c 2. . (ii) Persamaan (ii) disubstitusikan ke persamaan (i) sehingga diperoleh: Hal. : Isi dengan Judul Halaman Terkait Adaptif

Ellipse Equation 1. Ellipse equation that center to O(0, 0) Ellipse equation : TF 1 + TF 2 = 2 a + = 2 a Squaring left side and right so we get…… (a 2 - c 2) x 2 + a 2 y 2 = a 2(a 2 -c 2). . . (i), If point T at top point in minor axis (0, b) then …. b 2 =a 2 – c 2. . (ii) Equation (ii) is substituted to equation (i) then we get: Hal. : Isi dengan Judul Halaman Terkait Adaptif

Elips Contoh Tentukan persamaan elips dengan titik puncak (13, 0) dan fokus F 1(-12, 0) dan F 2(12, 0). Jawab: Diketahui pusat elips O(0, 0) Titik puncak (13, 0) a = 13 Titik fokus (-12, 0) dan (12, 0) c = 12 Sumbu utama adalah sumbu X, sehingga persamaannya: Hal. : Isi dengan Judul Halaman Terkait Adaptif

Ellipse Example Determine ellipse equation with top point (13, 0) and focus F 1(-12, 0) and F 2(12, 0). Answer: Given ellipse center O(0, 0) Top Point (13, 0) a = 13 Focus point (-12, 0) and (12, 0) c = 12 Main axis is X, so the equation: Hal. : Isi dengan Judul Halaman Terkait Adaptif

Elips 2. Persamaan elips yang bertitik pusat P (m, n) X= m Y a. Persamaan elips dengan titik pusat (m, n): D P(m, n) A F 2 F 1 B C O X m b. Sumbu utamanya (sumbu) y = n, dengan panjang 2 a dan sumbu minornya adalah sumbu x = n, dengan panjang 2 b. 3. Titik fokus F 1(m-c, n) dan F 2( m + c, n ) 4. Titik puncak A(m-a, n) dan B ( m + a, n ) 5. Panjang lactus rectum (LR) = Hal. : dengan Isi dengan Judul Halaman Terkait Adaptif

Ellipse 2. Ellipse equation that center to P (m, n) X= m Y a. Ellipse equation with center point (m, n): D P(m, n) A F 2 F 1 B C O m X b. Main axis y = n, with the length 2 a and minor axis is x = n, with the length 2 b. 3. Focus point F 1(m-c, n) and F 2( m + c, n ) 4. Top point A(m-a, n) and B ( m + a, n ) 5. Length of lactus rectum (LR) = Hal. : with Isi dengan Judul Halaman Terkait Adaptif

Elips Contoh: Tentukan persamaan elips dengan fokus F 1(1, 3) dan F 2(7, 3) dan puncaknya (10, 3). Jawab: Fokus (1, 3) dan (7, 3) = m-c = 1, m + c = 7 dengan eliminasi diperoleh m=4 dan c= 3 Pusat P (m, n) = P (4, 3) m=3 Puncak(10, 3) m + a= 10 a= 6 b 2 = a 2 –c 2 = 62 - 32 = 36 - 9 = 27 Sumbu utama y=3, sehingga persamaan elips menjadi: Hal. : Isi dengan Judul Halaman Terkait Adaptif

Ellipse Example: Determine the ellipse equation with focus F 1(1, 3) and F 2(7, 3) and the top (10, 3). Answer: Focus (1, 3) and (7, 3) = m-c = 1, m + c = 7 with the elimination gotten m=4 and c= 3 Center P (m, n) = P (4, 3) m=3 Top(10, 3) m + a= 10 a= 6 b 2 = a 2 –c 2 = 62 - 32 = 36 - 9 = 27 Main axis y=3, so ellipse equation become: Hal. : Isi dengan Judul Halaman Terkait Adaptif

Elips Bentuk umum persamaan elips Persamaan elips memiliki bentuk umum: Hubungan antara persamaan dengan adalah sebagai berikut: Jika A > B, maka A = a 2, B = b 2, C=-2 a 2 m, D= -2 b 2 n, E= a 2 m 2 + b 2 n 2 - a 2 b 2 Jika A < B, maka A = b 2, B = a 2, C=-2 b 2 m, D= -2 a 2 n, E= a 2 m 2 + b 2 n 2 - a 2 b 2 Hal. : Isi dengan Judul Halaman Terkait Adaptif

Ellipse General form of ellipse equation Ellipse equation has general form: Relation between equation and as follows: If A > B, then A = a 2, B = b 2, C=-2 a 2 m, D= -2 b 2 n, E= a 2 m 2 + b 2 n 2 - a 2 b 2 If A < B, then A = b 2, B = a 2, C=-2 b 2 m, D= -2 a 2 n, E= a 2 m 2 + b 2 n 2 - a 2 b 2 Hal. : Isi dengan Judul Halaman Terkait Adaptif

Elips Contoh: Tentukan titik pusat dan fokus dari elips yang memiliki persamaan 4 x 2+ 9 y 2 -16 x+ 18 y -11=0. Jawab: Diketahui persamaan elips: 4 x 2+ 9 y 2 -16 x+ 18 y -11=0. A=4, B= 9, C= -16, D=18, E= -11 b 2 = A = 4 b=2 A 2 = B = 9 a=3 C = -2 b 2 m D= -2 a 2 m C 2= a 2 –b 2 = 9 -4 = 5 -16=-2. 4. m 18= -2. 9. n C = -16= -8 m 18= -18 n 2= m -1 = n Pusat P(m, n) P(2, -1) Fokus. F 2(m-c, n)=F 2 dan F 2(m+c, n)=F 2 Hal. : Isi dengan Judul Halaman Terkait Adaptif

Ellipse Example: Find the top point and focus of ellipse that has equation 4 x 2+ 9 y 2 -16 x+ 18 y -11=0. Answer: Given ellipse equation: 4 x 2+ 9 y 2 -16 x+ 18 y -11=0. A=4, B= 9, C= -16, D=18, E= -11 b 2 = A = 4 b=2 A 2 = B = 9 a=3 C = -2 b 2 m D= -2 a 2 m C 2= a 2 –b 2 = 9 -4 = 5 -16=-2. 4. m 18= -2. 9. n C = -16= -8 m 18= -18 n 2= m -1 = n Center P(m, n) P(2, -1) Focus. F 2(m-c, n)=F 2 and F 2(m+c, n)=F 2 Hal. : Isi dengan Judul Halaman Terkait Adaptif

Elips Persamaan garis singgung melalui titik (x 1, y 1) pada elips 1. Untuk persamaan elips persamaan garis singgung yang melalui (x 1, y 1) pada elips tersebut adalah: 2. Untuk persamaan elips persamaan garis singgung yang melalui (x 1, y 1) pada elips tersebut adalah: Hal. : Isi dengan Judul Halaman Terkait Adaptif

Ellipse The equation of tangent line through the point (x 1, y 1) in ellipse 1. For ellipse equation of tangent line through (x 1, y 1) in ellipse is: 2. For ellipse equation tangent line equation through (x 1, y 1) in ellipse is: Hal. : Isi dengan Judul Halaman Terkait Adaptif

Elips Persamaan garis singgung dengan gradien p Pada elips atau , adalah y= p Untuk elips dengan persamaan: Persamaan garis singgungnya adalah: y - n = p(x-m) Hal. : Isi dengan Judul Halaman Terkait Adaptif

Ellipse Equation of tangent line with gradient p In ellipse or , is y= p For ellipse with the equation: The tangent line is: y - n = p(x-m) Hal. : Isi dengan Judul Halaman Terkait Adaptif

Elips Contoh: Tentukan persamaan garis singgung elips berikut. a. pada titik (4, 3) b. pada titik(5, -3) Jawab: a. Diketahui : (4, 3) x 1 = 4 dan y 1= 3 Persamaan garis singgung: Hal. : Isi dengan Judul Halaman Terkait Adaptif

Ellipse Example: Determine the tangent line equation of this ellipse. a. At point (4, 3) b. At point(5, -3) Answer: a. Given that : (4, 3) x 1 = 4 and y 1= 3 Equation of tangent line: Hal. : Isi dengan Judul Halaman Terkait Adaptif

Elips b. Diketahui: pusat (m, n) = (1, -2) ( 5, -3) y 1 = -3 Persamaan garis singgung: Hal. : Isi dengan Judul Halaman Terkait Adaptif

Ellipse b. Given that: center (m, n) = (1, -2) ( 5, -3) y 1 = -3 Equation of tangent line: Hal. : Isi dengan Judul Halaman Terkait Adaptif

Elips Hal. : Isi dengan Judul Halaman Terkait Adaptif

Ellipse Hal. : Isi dengan Judul Halaman Terkait Adaptif

Hal. : Isi dengan Judul Halaman Terkait Adaptif

Hal. : Isi dengan Judul Halaman Terkait Adaptif

Parabola Persamaan parabola berpuncak 0(0, 0) y 2 = 4 px a. Puncak (0, 0) b. Sumbu semetri = sumbu x c. Fokusnya F(p, 0) d. Direktriknya x = -p Y • • (0, 0) • F(P, 0) X d: X=-P Hal. : Isi dengan Judul Halaman Terkait Adaptif

Parabola equation top 0(0, 0) y 2 = 4 px a. Top (0, 0) b. Symmetry Axis = x c. Focus F(p, 0) d. Directory x = -p Y • • (0, 0) • F(P, 0) X d: X=-P Hal. : Isi dengan Judul Halaman Terkait Adaptif

Parabola Persamaan parabola yang bepuncak 0(0, 0) dan Fokus di F(-p, 0) adalah Y 2 = -4 px Y • • F(-P, 0) (0, 0) • X • d: X=-P Hal. : Isi dengan Judul Halaman Terkait Adaptif

Parabola equation top in 0(0, 0) and focus on F(-p, 0) is Y 2 = -4 px Y • • F(-P, 0) (0, 0) • X • d: X=-P Hal. : Isi dengan Judul Halaman Terkait Adaptif

Parabola Persamaan parabola yang bepuncak 0(0, 0) dan Fokus di F(0, p) adalah x 2 = -4 py Y F(0, p) • • (0, 0) • Hal. : X d: y=-P Isi dengan Judul Halaman Terkait Adaptif

Parabola equation top in 0(0, 0) and focus on F(0, p) is x 2 = -4 py Y F(0, p) • • (0, 0) • Hal. : X d: y=-P Isi dengan Judul Halaman Terkait Adaptif

Parabola Persamaan parabola yang bepuncak 0(0, 0) dan Fokus di F(0, -p) adalah x 2 = -4 py Y • d: y=p • (0, 0) X • F(0, -p) Hal. : Isi dengan Judul Halaman Terkait Adaptif

Parabola equation top in 0(0, 0) and focus on F(0, -p) is x 2 = -4 py Y • d: y=p • (0, 0) X • F(0, -p) Hal. : Isi dengan Judul Halaman Terkait Adaptif

Parabola Contoh: 1. Dari parabola-parabola berikut tentukan koordinat fokus, persamaan sumbu semetri, persamaan direktris dan panjang lactus rectum a. y 2 = 4 x c. x 2 = -8 y b. y 2 = -12 x d. x 2 = 6 y Jawab: a. y 2 =4 px y 2 = 4 x, maka p = 1 Parabola ini merupakan parabola horizsontal ysng terbuka ke kanan. (i) Koordinat titik fokus F(p, 0) F(1, 0) (ii) Sumbu semetri berimpit dengan sumbu X, maka persamaanya y = 0 (iii) Persamaan direktris: x = -p x = -1 (iv) Panjang lactus rectum (LR) = 4 p = 4. 1 = 4 Hal. : Isi dengan Judul Halaman Terkait Adaptif

Parabola Example: 1. From next parabolas, find the focus coordinates, equation of symmetric axis, directory equation and the length of lactose rectum a. y 2 = 4 x c. x 2 = -8 y b. y 2 = -12 x d. x 2 = 6 y Answer: a. y 2 =4 px y 2 = 4 x, then p = 1 This parabola is horizontal parabola that right opened. (i) Coordinate of focus point F(p, 0) F(1, 0) (ii) Symmetric axis that close to axis x, then the equation y = 0 (iii) Directory equation : x = -p x = -1 (iv) The length of lactose rectum (LR)= 4 p = 4. 1=4 Hal. : Isi dengan Judul Halaman Terkait Adaptif

Parabola b. y 2 =-p 4 x y 2 = -12 x, maka 4 p = 12 p=3 Parabola ini merupakan parabola horizsontal yang terbuka ke kiri (i) Koordinat titik fokus F(-p, 0) F(-3, 0) (ii) Sumbu semetri berimpit dengan sumbu X, maka persamaanya y = 0 (iii) Persamaan direktris: x = -p x=3 (iv) Panjang lactus rectum (LR) = 4 p = 4. 3= 12 c. x 2 = -p 4 y x 2 = -8 y, maka 4 p = 8 p=2 Parabola ini merupakan parabola horizsontal ysng terbuka ke bawah (i) Koordinat titik fokus F(0, -p) F(0, -2) (ii) Sumbu semetri berimpit dengan sumbu y, maka persamaanya x = 0 (iii) Persamaan direktris: y = p y=2 (iv) Panjang lactus rectum (LR) = 4 p = 4. 2 = 8 d. Untuk latihan Hal. : Isi dengan Judul Halaman Terkait Adaptif

Parabola b. y 2 =-p 4 x y 2 = -12 x, then 4 p = 12 p=3 This parabola is horizontal parabola that left opened (i) Coordinate of focus point F(-p, 0) F(-3, 0) (ii) Symmetric axis that close to axis X, then the equation of y = 0 (iii) Directory equation: x = -p x=3 (iv) The length of lactose rectum (LR) = 4 p = 4. 3= 12 c. x 2 = -p 4 y x 2 = -8 y, then 4 p = 8 p=2 This parabola is horizontal parabola that below opened (i) Coordinate of focus point F(0, -p) F(0, -2) (ii) Symmetry axis that close to axis y, then the equation of X = 0 (iii) Directory equation: y = p y=2 (iv) The length of lactose rectum (LR) = 4 p = 4. 2 = 8 d. Exercise Hal. : Isi dengan Judul Halaman Terkait Adaptif

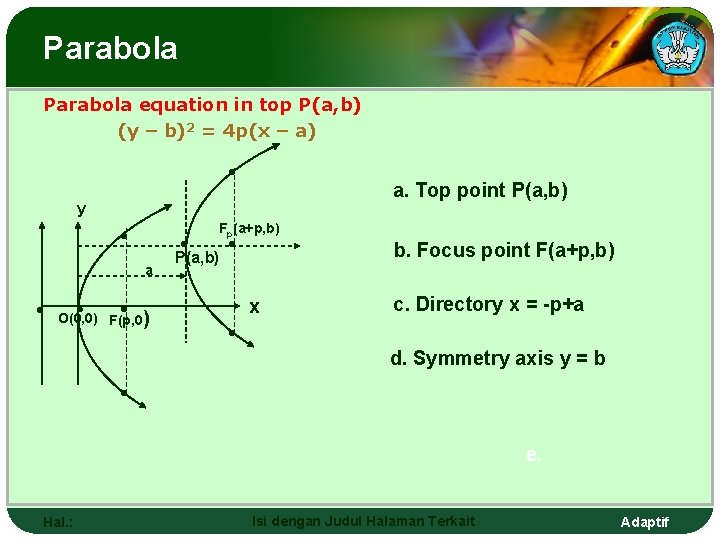
Parabola Persamaan parabola berpuncak P(a, b) (y – b)2 = 4 p(x – a) • a. Titik puncak P(a, b) y • • a • Fp(a+p, b) P(a, b) • x • • F(p, 0) O(0, 0) b. Titik fokus F(a+p, b) c. Direktris x = -p+a • d. Sumbu semetri y = b • e. Hal. : Isi dengan Judul Halaman Terkait Adaptif

Parabola equation in top P(a, b) (y – b)2 = 4 p(x – a) • a. Top point P(a, b) y • • a • Fp(a+p, b) P(a, b) • x • • F(p, 0) O(0, 0) b. Focus point F(a+p, b) c. Directory x = -p+a • d. Symmetry axis y = b • e. Hal. : Isi dengan Judul Halaman Terkait Adaptif

Parabola Contoh: Diberikan persamaan parabola 3 x – y 2 + 4 y + 8= 0 Tentukan : a. Titik puncak c. Direktris b. Titik fokus d. Sumbu semetri Jawab: Ubah persamaan parabola ke persamaan umum: 3 x – y 2 + 4 y + 8= 0 y 2 - 4 y = 3 x + 8 y 2 - 4 y + 4 = 3 x + 8 + 4 (y – 2)2 = 3 x + 12 (y – 2)2 = 3(x + 4) Didapat persamaan parabola (y – 2)2 = 3(x + 4) yaitu parabola mendatar yang terbuka ke kanan. Hal. : Isi dengan Judul Halaman Terkait Adaptif

Parabola Example: Given that parabola equation 3 x – y 2 + 4 y + 8= 0 Determine: a. Top point c. Directory b. Focus point d. Symmetry axis Answer: Change parabola equation into general equation: 3 x – y 2 + 4 y + 8= 0 y 2 - 4 y = 3 x + 8 y 2 - 4 y + 4 = 3 x + 8 + 4 (y – 2)2 = 3 x + 12 (y – 2)2 = 3(x + 4) Gotten that parabola equation (y – 2)2 = 3(x + 4) is The flat parabola that right opened. Hal. : Isi dengan Judul Halaman Terkait Adaptif

Parabola Dari persamaan tersebut diperoleh: y a. Titik puncak P(-4, 2) b. 4 p = 3 maka p = Titik Fokus F(a+p, b) F P(-4, 2) O(0, 0) x c. Persamaan direktris : d. Sumbu semetrinya : y = 2 Hal. : Isi dengan Judul Halaman Terkait Adaptif

Parabola From that equation we get: y a. Top point P(-4, 2) b. 4 p = 3 then p = Focus point F(a+p, b) F P(-4, 2) O(0, 0) x c. Directory equation : d. Symmetry axis : y = 2 Hal. : Isi dengan Judul Halaman Terkait Adaptif

Parabola Soal untuk latihan: a. Tentukan persaaman parabola yang berpuncak di (2, 4) dan fokusnys (-3, 4) b. Tentukan persamaan Parabola yang titik fokusnya F(2 -3) dan persamaan didertrisnya y=5 Hal. : Isi dengan Judul Halaman Terkait Adaptif

Parabola Exercise: a. Find the parabola equation that top in (2, 4) and the focus (-3, 4) b. Find the equation parabola that has focus point F(2 -3) and the directory equation y=5 Hal. : Isi dengan Judul Halaman Terkait Adaptif

Persamaan garis singgung parabola A. Persamaan garis singgung parabola melaluhi titik A(x 1, y 1) yy 1 = 2 p(x+x 1) y • A(x 1, y 1) • Hal. : x Isi dengan Judul Halaman Terkait Adaptif

Equation of tangent line in parabola A. Equation of the parabola tangent line through point of A(x 1, y 1) yy 1 = 2 p(x+x 1) y • A(x 1, y 1) • Hal. : x Isi dengan Judul Halaman Terkait Adaptif

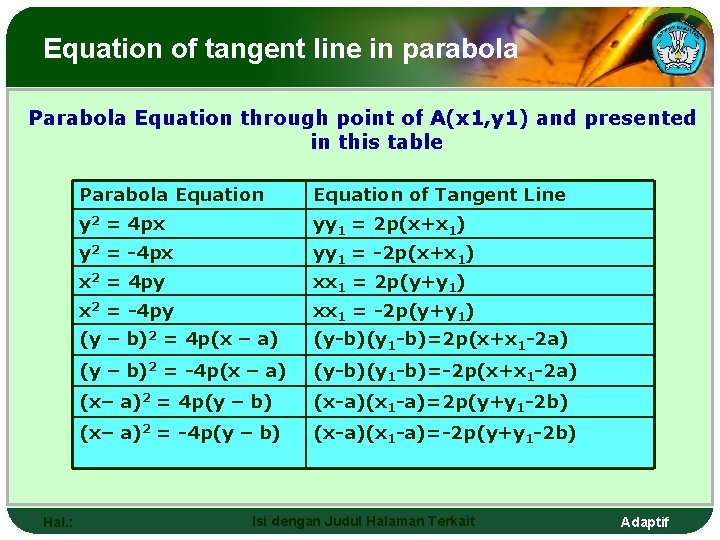
Persamaan garis singgung parabola Persamaan parabola melaluhi titik A(x 1, y 1) di sajikan pada tabel berikut Hal. : Persamaan Parabola Persamaan Garis singgung y 2 = 4 px yy 1 = 2 p(x+x 1) y 2 = -4 px yy 1 = -2 p(x+x 1) x 2 = 4 py xx 1 = 2 p(y+y 1) x 2 = -4 py xx 1 = -2 p(y+y 1) (y – b)2 = 4 p(x – a) (y-b)(y 1 -b)=2 p(x+x 1 -2 a) (y – b)2 = -4 p(x – a) (y-b)(y 1 -b)=-2 p(x+x 1 -2 a) (x– a)2 = 4 p(y – b) (x-a)(x 1 -a)=2 p(y+y 1 -2 b) (x– a)2 = -4 p(y – b) (x-a)(x 1 -a)=-2 p(y+y 1 -2 b) Isi dengan Judul Halaman Terkait Adaptif

Equation of tangent line in parabola Parabola Equation through point of A(x 1, y 1) and presented in this table Hal. : Parabola Equation of Tangent Line y 2 = 4 px yy 1 = 2 p(x+x 1) y 2 = -4 px yy 1 = -2 p(x+x 1) x 2 = 4 py xx 1 = 2 p(y+y 1) x 2 = -4 py xx 1 = -2 p(y+y 1) (y – b)2 = 4 p(x – a) (y-b)(y 1 -b)=2 p(x+x 1 -2 a) (y – b)2 = -4 p(x – a) (y-b)(y 1 -b)=-2 p(x+x 1 -2 a) (x– a)2 = 4 p(y – b) (x-a)(x 1 -a)=2 p(y+y 1 -2 b) (x– a)2 = -4 p(y – b) (x-a)(x 1 -a)=-2 p(y+y 1 -2 b) Isi dengan Judul Halaman Terkait Adaptif

Persamaan garis singgung parabola Contoh: 1. Tentukan persamaan garis singgung parabola y 2 = 8 x di titik (2, 4) jawab : y 2 = 8 x 4 p = 8 p=2 Titik A(x 1, y 1) A(2, 4) Persamaan garis singgungnya adalah yy 1 = 2 p(x+x 1) y. 4 = 2. 2(x+2) 4 y = 4(x+2) y = x+2 Hal. : Isi dengan Judul Halaman Terkait Adaptif

Equation of tangent line in parabola Example: 1. Determine the equation of tangent line of parabola y 2 = 8 x at point (2, 4) Answer : y 2 = 8 x 4 p = 8 p=2 Point A(x 1, y 1) A(2, 4) The equation of tangent line is yy 1 = 2 p(x+x 1) y. 4 = 2. 2(x+2) 4 y = 4(x+2) y = x+2 Hal. : Isi dengan Judul Halaman Terkait Adaptif

Persamaan garis singgung parabola 2. Tentukan persamaan garis singgung parabola (x+1)2 = -3(y-2) pada titik (2, -1) Jawab : a = -1 , b = 2, x 1 = 2 dan y 1 = 1 (x+1)2 = -3(y-2) -4 p = -3 p= Persamaan garis singgung parabola di titik A(2, -1) adalah (x - a)(x 1 - a) = -2 p(y + y 1 - 2 b) (x +1)(2 +1) = -2. (y - 1 – 2. 2) (x + 1)(3) = 6(x + 1) = - 3(y – 5) 2(x + 1) = -(y – 5) 2 x + 2 = -y + 5 y = -2 x + 3 Hal. : Isi dengan Judul Halaman Terkait Adaptif

Equation of tangent line in parabola 2. Determine the equation of parabola tangent line (x+1)2 = -3(y-2) at point (2, -1) Answera : a = -1 , b = 2, x 1 = 2 and y 1 = 1 (x+1)2 = -3(y-2) -4 p = -3 p= The equation of parabola tangent line at point A(2, -1) is (x - a)(x 1 - a) = -2 p(y + y 1 - 2 b) (x +1)(2 +1) = -2. (y - 1 – 2. 2) (x + 1)(3) = 6(x + 1) = - 3(y – 5) 2(x + 1) = -(y – 5) 2 x + 2 = -y + 5 y = -2 x + 3 Hal. : Isi dengan Judul Halaman Terkait Adaptif

Persamaan garis singgung parabola B. Persamaan garis singgung parabola yang bergradien m Persamaan parabola Hal. : Persamaan garis singgung y 2 = 4 px y = mx + y 2 =- 4 px y = mx - x 2 = 4 py y = mx – m 2 p x 2 = -4 py y = mx + m 2 p (y – b)2 = 4 p(x – a) (y – b) = m(x – a) + (y – b)2 = -4 p(x – a) (y – b) = m(x – a) - (x– a)2 = 4 p(y – b) = m(x – a) – m 2 p (x– a)2 = -4 p(y – b) = m(x – a) + m 2 p Isi dengan Judul Halaman Terkait Adaptif

Equation of tangent line in parabola B. The equation of parabola tangent line that has gradient m Parabola Equation Hal. : Equation of tangent line y 2 = 4 px y = mx + y 2 =- 4 px y = mx - x 2 = 4 py y = mx – m 2 p x 2 = -4 py y = mx + m 2 p (y – b)2 = 4 p(x – a) (y – b) = m(x – a) + (y – b)2 = -4 p(x – a) (y – b) = m(x – a) - (x– a)2 = 4 p(y – b) = m(x – a) – m 2 p (x– a)2 = -4 p(y – b) = m(x – a) + m 2 p Isi dengan Judul Halaman Terkait Adaptif

Persamaan garis singgung parabola Contoh: 1. Tentukan persamaan garis singgung parabola y 2 = 8 x yang kergradien 2 Jawab: Parabola y 2 = 8 x 4 p = 8 p=2 Maka persamaan garis singgungnya adalah: y = mx + y = 2 x + 1 Hal. : Isi dengan Judul Halaman Terkait Adaptif

Equation of tangent line in parabola Example: 1. Find the equation of parabola tangent line y 2 = 8 x that has gradient 2 Answer: Parabola y 2 = 8 x 4 p = 8 p=2 Then the equation of tangent line is: y = mx + y = 2 x + 1 Hal. : Isi dengan Judul Halaman Terkait Adaptif

Persamaan garis singgung parabola 2. Tentukan persamaan garis singgung parabola (y + 5)2 = -8(x – 2) yang bergradien 3 Jawab : Parabola (y + 5)2 = -8(x – 2) -4 x = -8 p=2 Puncak P(2, -5) Jadi persamaan garis singgungnya adalah y – b = m(x – a) – y + 5 = 3(x – 2) – 3 y + 15 = 9(x – 2) -2 3 y + 15 = 9 x – 20 9 x – 3 y + 35 = 0 y = 3 x - Hal. : Isi dengan Judul Halaman Terkait Adaptif

Equation of tangent line in parabola 2. Determine the equation of parabola tangent line (y + 5)2 = -8(x – 2) that has gradient 3 Answer : Parabola (y + 5)2 = -8(x – 2) -4 x = -8 p=2 Top of P(2, -5) So the equation of tangent line is y – b = m(x – a) – y + 5 = 3(x – 2) – 3 y + 15 = 9(x – 2) -2 3 y + 15 = 9 x – 20 9 x – 3 y + 35 = 0 y = 3 x - Hal. : Isi dengan Judul Halaman Terkait Adaptif

Hiperbola A. Hiperbola adalah kedudukan titik-titik pada bidang datar yang selisih jaraknya terhadap dua titik tertentu adalah tetap. Kedua titik tertentu di sebut fokus(titik apai). D y Y = M K A. Persamaan Hiperbola Pusat(0, 0) a. Pusat O(0, 0) b. Fokus F’(-C, 0) dan F(C, 0) • F’(-C, 0) A • 0 • • B • F(C, 0) x c. Puncak A(-a, 0) dan B(a, 0) d. Sumbu semetri - Sumbu Utama sumbu x - Sumbu sekawan adalah sumbu y E N L Y= Hal. : e. Sumbu nyata AB = 2 a f. Sumbu imajiner MN = 2 b g. Asimtot , y = + Isi dengan Judul Halaman Terkait Adaptif

Hyperbola A. Hyperbola is position of points on the flat surface which has distance difference towards two certain points is constant. . Two certain points is Focus (reach point). D y Y = M K A. Equation of Center Hyperbola(0, 0) a. Center O(0, 0) b. Focus F’(-C, 0) and F(C, 0) • F’(-C, 0) A • 0 • • B • F(C, 0) x c. Top of A(-a, 0) and B(a, 0) d. Symmetry axis - Main axis of axis x - The flock axis is axis y E N L Y= Hal. : e. Real axis AB = 2 a f. Imaginer axis MN = 2 b g. Asymptote , y = + Isi dengan Judul Halaman Terkait Adaptif

Hiperbola B. Persamaan Hiperbola atau y D F(0, C) K • B • b 2 y 2 – a 2 x 2 = a 2 b 2 a. Pusat O(0, 0) b. Fokus F’(0, -C) dan F(0, C) Y = c. Puncak A(0, -a) dan B(0, a) M 0 • N x d. Sumbu semetri - Sumbu Utama sumbu y - Sumbu sekawan adalah sumbu x A E • • F’(0, -C) L Y= e. Sumbu nyata AB = 2 a f. Sumbu imajiner MN = 2 b g. Asimtot , y = + Hal. : Isi dengan Judul Halaman Terkait Adaptif

Hyperbola B. Hyperbola Equation or y D F(0, C) K • B • b 2 y 2 – a 2 x 2 = a 2 b 2 a. Center O(0, 0) b. Focus F’(0, -C) and F(0, C) Y = c. Top of A(0, -a) and B(0, a) M 0 • N x d. Symmetry axis - Main Axis of axis y - Flock axis is x A E • • F’(0, -C) L Y= e. Real axis AB = 2 a f. Imaginer Axis MN = 2 b g. Asymptote , y = + Hal. : Isi dengan Judul Halaman Terkait Adaptif

Hiperbola Contoh : 1. Tentukan persamaan hiperbola jika titik fokusnya F’(-13, 0) dan F(13, 0) dengan puncak (-5, 0) dan (5, 0) Jawab : Pusat (0, 0) a = 5 , c = 13 b 2 = c 2 – a 2 = 132 – 52 = 169 – 25 = 144 Sumbu utama sumbu X, maka persamaan hiperbolanya adalah: Hal. : Isi dengan Judul Halaman Terkait Adaptif

Hyperbola Example : 1. Find the hyperbola equation if the focus point is F’(-13, 0) and F(13, 0) while the top (-5, 0) and (5, 0) Answer : Center (0, 0) a = 5 , c = 13 b 2 = c 2 – a 2 = 132 – 52 = 169 – 25 = 144 The main axis of axis X, then the hyperbola equation is: Hal. : Isi dengan Judul Halaman Terkait Adaptif

Hiperbola 2. Diketahui persamaan hiperbola dari Jawab : dan Pusat(0, 0) Puncak(-a, 0)=(-4, 0) dan (a, 0) = (4, 0) Hal. : Isi dengan Judul Halaman Terkait Adaptif

Hyperbola 2. Given that hyperbola equation of Answer : and Center (0, 0) Top (-a, 0)=(-4, 0) and (a, 0) = (4, 0) Hal. : Isi dengan Judul Halaman Terkait Adaptif

Hiperbola A. Persamaaan Hiperbola dengan pusat P(m, n) Y = y D M a. Pusat P(m, n) b. Fokus F’(m-C, 0) dan F(m+C, 0) K c. Puncak A(m-a, 0) dan B(m+a, 0) d. Sumbu semetri • F’(-C, 0) • A P • • B • F(C, 0) - Sumbu Utama sumbu y = n - Sumbu sekawan adalah y = m E N L 0 Y= e. Sumbu nyata AB = 2 a x f. Sumbu imajiner MN = 2 b g. Asimtot , y-n = + Hal. : Isi dengan Judul Halaman Terkait (x - a) Adaptif

Hyperbola A. Hyperbola Equation at center P(m, n) Y = y D M a. Center P(m, n) b. Focus F’(m-C, 0) and F(m+C, 0) K c. Top of A(m-a, 0) and B(m+a, 0) d. Symmetry Axis • F’(-C, 0) • A P • • B • F(C, 0) - Main axis of axis y = n - Flock axis is y = m E N L 0 Y= e. Real Axis AB = 2 a x f. Imaginer axis MN = 2 b g. Asymptote , y-n = + Hal. : Isi dengan Judul Halaman Terkait (x- a) Adaptif

Hiperbola Contoh: 1. Tentukan persamaan hiperbola jika titik fokus F’(-2, -3) dan F(8, -3) dan titik puncaknya (7, -3) Jawab: fokus F’(-2, -3) dan F(8, -3) Jarak pusat ke fokus c = 8 – 3 = 5 Puncak (7, 3) Jarak pusat dengan puncak a = 7 – 3 = 4 b 2 = c 2 – a 2 = 52 – 42 = 25 – 16 = 9 Jadi persamaan hiperbola adalah atau 9(x-3)2 – 16(y+3)2 = 144 9 x 2 – 16 y 2 – 54 x -96 y – 207 = 0 Hal. : Isi dengan Judul Halaman Terkait Adaptif

Hiperbola Example: 1. Determine the equation of hyperbola if the focus point F’(-2, -3) and F(8, -3) and top point is (7, -3) Answer: focus F’(-2, -3) and F(8, -3) Distance from center to focus c = 8 – 3 = 5 Top (7, 3) Distance from center with the top a = 7 – 3 = 4 b 2 = c 2 – a 2 = 52 – 42 = 25 – 16 = 9 So the equation of hyperbola is or 9(x-3)2 – 16(y+3)2 = 144 9 x 2 – 16 y 2 – 54 x -96 y – 207 = 0 Hal. : Isi dengan Judul Halaman Terkait Adaptif

Hiperbola 2. Tentukan titik pusat, titik fokus, titik puncak, panjang lactus rectum dan persamaan asimtotnya dari Jawab: Titik pusat (4, -1) kkkk Adaptif

Hyperbola 2. Determine center point, focus point, top point, length of lactus rectum and asymptote from Answer: Center point (4, -1) kkkk Adaptif

Persamaan Garis Singgung Hiperbola Persamaan garis singgung hiperbola melelalui. T(x 1, y 1) Persamaan garis singgung di titik T(x 1, y 1) yaitu Hal. : Isi dengan Judul Halaman Terkait Adaptif

Equation of Tangent Line in Hyperbola Equation of tangent line in hyperbola through T(x 1, y 1) Equation tangent line at point T(x 1, y 1) is Hal. : Isi dengan Judul Halaman Terkait Adaptif

PERSAMAN GARIS SINGGUNG HIPERBOLA Contoh 1 : Tentukan persamaan garis singgung pada hiperbola pada titik (9, -4) Jawab Persamaan garis singgung Hiperbola di titik T(x 1, y 1) yaitu Jadi persamaan garis singgungnya : atau x + 2 y = 1 Hal. : Isi dengan Judul Halaman Terkait Adaptif

EQUATION OF TANGENT LINE IN HYPERBOLA Example 1 : Find the equation of tangent line in hyperbola At point (9, -4) Answer: Equation of tangent line in hyperbola At point T(x 1, y 1) is So the equation of tangent line is : or x + 2 y = 1 Hal. : Isi dengan Judul Halaman Terkait Adaptif

Persamaan garis singgung Hiperbola Contoh 2 Tentukan persamaan garis singgung hiperbola Pada titik (-4, -3) Jawab : Persamaan garis singgung hiperbola di titik T(x 1, y 1) yaitu Jadi persamaan garissinggungnya : x=-4 Hal. : Isi dengan Judul Halaman Terkait Adaptif

EQUATION OF TANGENT LINE IN HYPERBOLA Example 2 Determine the equation of tangent line in hyperbola At point (-4, -3) Answer : The equation of tangent line in hyperbola At point T(x 1, y 1) is So the equation of tangent line is : x=-4 Hal. : Isi dengan Judul Halaman Terkait Adaptif

Hal. : Isi dengan Judul Halaman Terkait Adaptif

Hal. : Isi dengan Judul Halaman Terkait Adaptif