HUBUNGAN ANTAR SUDUT BAB GARIS DAN SUDUT MATERI

HUBUNGAN ANTAR SUDUT

BAB GARIS DAN SUDUT MATERI HUBUNGAN ANTAR SUDUT SMP KELAS VII SEMESTER I Loading Please wait

KD & Profil Indikator Materi Latihan Kompetensi Dasar Sudut Saling Berpelurus Soal Indikator Sudut Saling Berpenyiku Jawaban Sudut Saling Bertolak Belakang Dua Garis Sejajar Dipotong Oleh Garis Lain Sudut Sehadap Sudut Dalam Bersebrangan Sudut Luar Bersebrangan Sudut Sepihak Sudut Dalam Sepihak Sudut Luar Sepihak

PROFIL Nama NIM Kelas : Septiani Yugni Maudy : 1100577 : Pendidikan Matematika 7 B 2011

KOMPETENSI DASAR Melalui proses pembelajaran garis dan sudut siswa mampu: 1. memiliki sikap terbuka, santun, objektif, menghargai pendapat dan karya teman dalam interaksi kelompok maupun aktifitas sehari-hari; 2. memahami berbagai konsep dan prinsip garis dan sudut dalam pemecahan masalah nyata; 3. menerapkan berbagai konsep dan sifat-sifat terkait garis dan sudut dalam pembuktian matematis serta pemecahan masalah nyata.

INDIKATOR 1. Mampu menerapkan konsep dua sudut yang saling berpelurus. 2. Mampu menerapkan konsep dua sudut yang saling berpenyiku. 3. Mampu menerapkan konsep dua sudut yang saling bertolak belakang. 4. Mampu menemukan sifat-sifat sudut jika dua garis sejajajar dipotong oleh garis lain.

SUDUT SALING BERPELURUS α α α=180 o β α+β=180 o Jumlah dua sudut yang saling berpelurus (bersuplemen) adalah 180 o. Sudut yang satu merupakan pelurus dari sudut yang lain.

SUDUT SALING BERPENYIKU α+β= 90 O α β Jumlah dua sudut yang saling berpenyiku (berkomplemen) adalah 90 O. Sudut yang satu merupakan penyiku dari sudut yang lain.

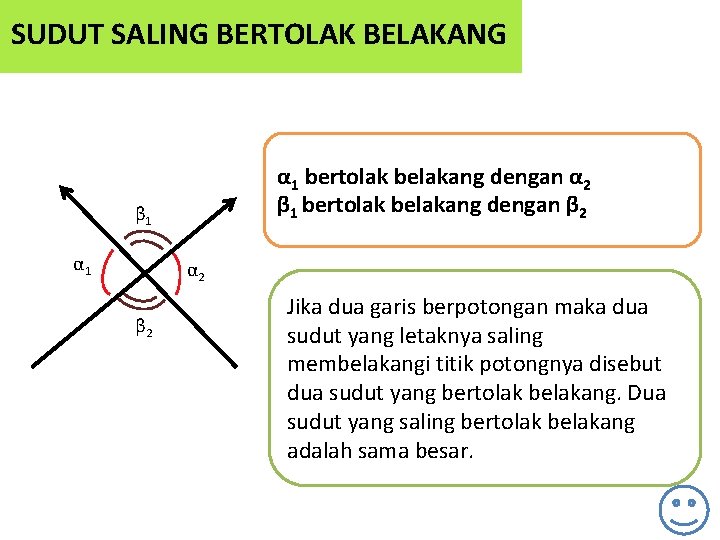
SUDUT SALING BERTOLAK BELAKANG α 1 bertolak belakang dengan α 2 β 1 bertolak belakang dengan β 2 β 1 α 1 α 2 β 2 Jika dua garis berpotongan maka dua sudut yang letaknya saling membelakangi titik potongnya disebut dua sudut yang bertolak belakang. Dua sudut yang saling bertolak belakang adalah sama besar.

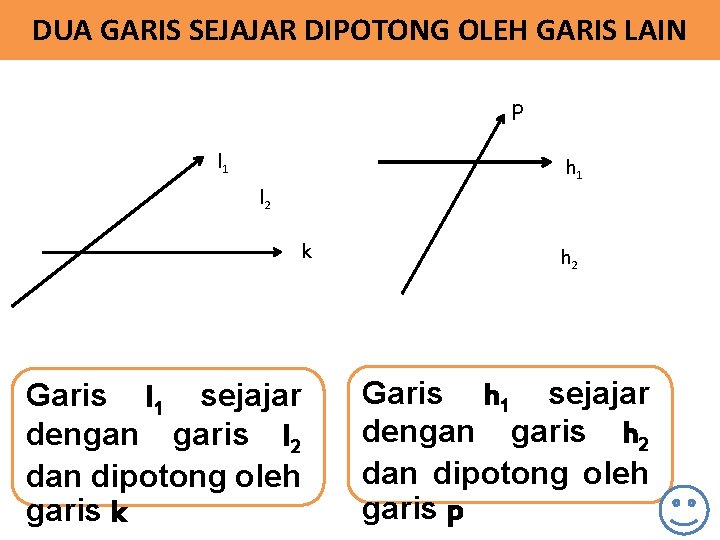
DUA GARIS SEJAJAR DIPOTONG OLEH GARIS LAIN p l 1 h 1 l 2 k Garis l 1 sejajar dengan garis l 2 dan dipotong oleh garis k h 2 Garis h 1 sejajar dengan garis h 2 dan dipotong oleh garis p

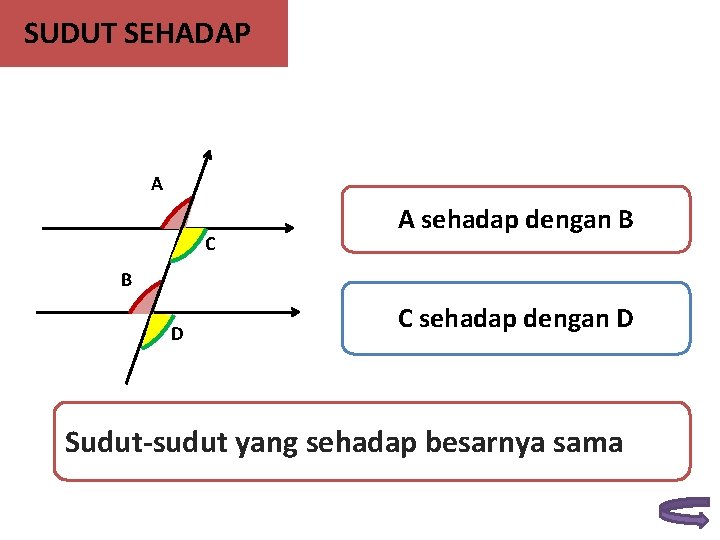
SUDUT SEHADAP A C A sehadap dengan B B D C sehadap dengan D Sudut-sudut yang sehadap besarnya sama

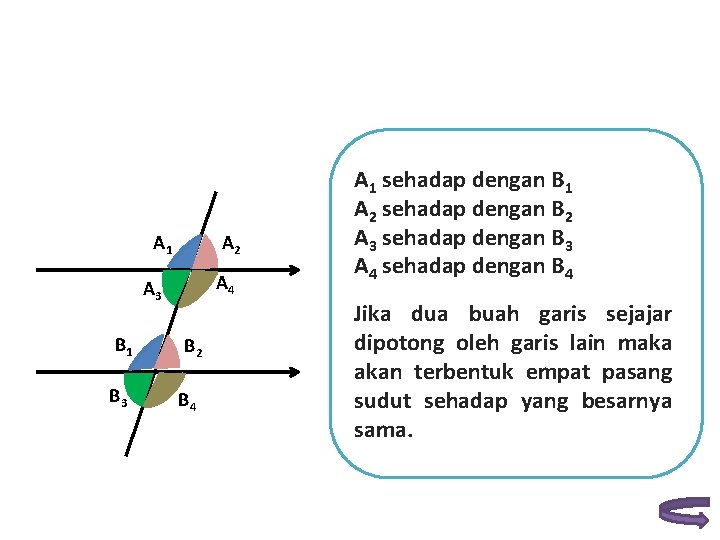
A 1 A 2 A 4 A 3 B 1 B 2 B 3 B 4 A 1 sehadap dengan B 1 A 2 sehadap dengan B 2 A 3 sehadap dengan B 3 A 4 sehadap dengan B 4 Jika dua buah garis sejajar dipotong oleh garis lain maka akan terbentuk empat pasang sudut sehadap yang besarnya sama.

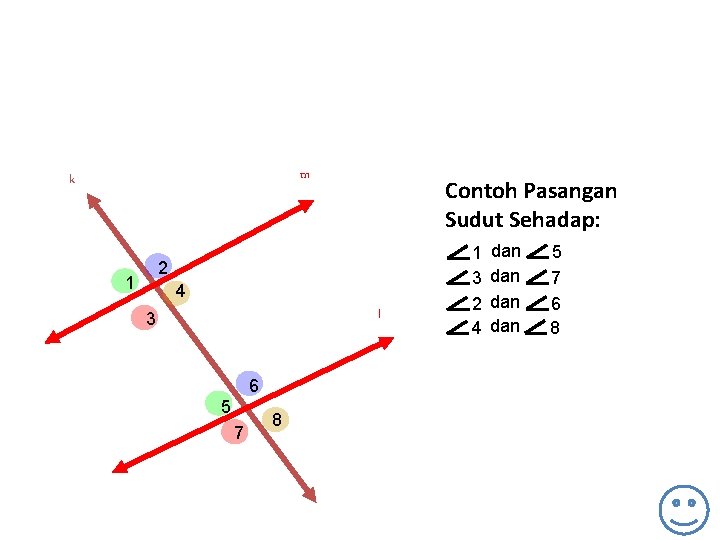
m k Contoh Pasangan Sudut Sehadap: 2 1 4 l 3 6 5 7 8 1 3 2 4 dan dan 5 7 6 8

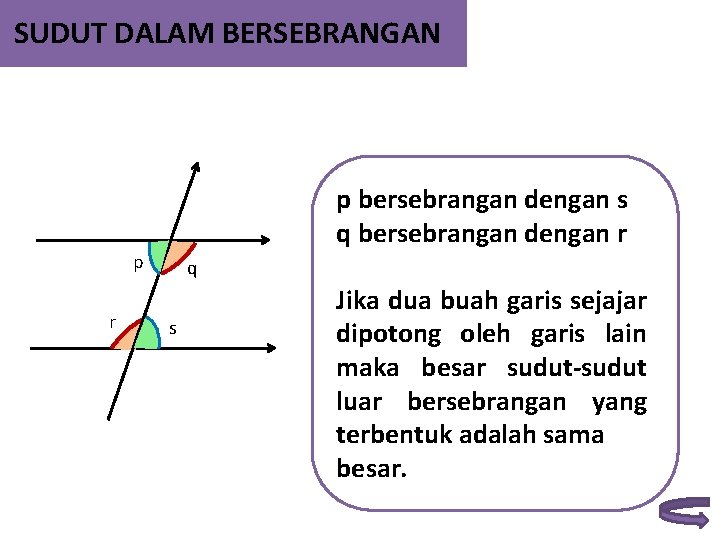
SUDUT DALAM BERSEBRANGAN p bersebrangan dengan s q bersebrangan dengan r p r q s Jika dua buah garis sejajar dipotong oleh garis lain maka besar sudut-sudut luar bersebrangan yang terbentuk adalah sama besar.

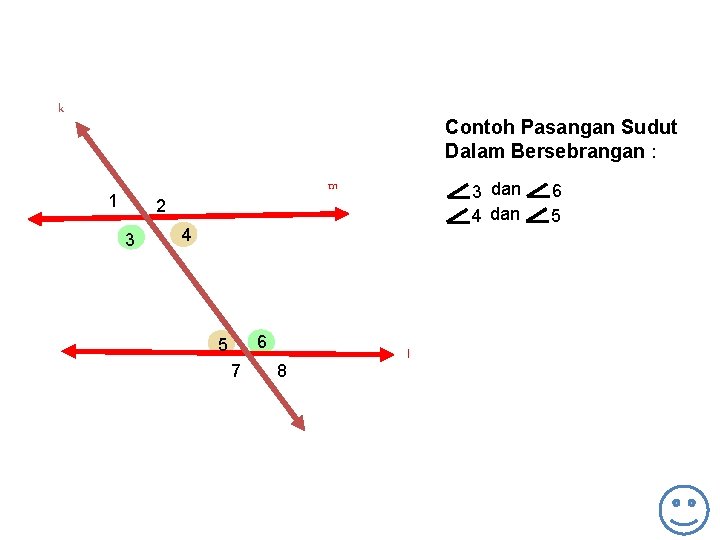
k Contoh Pasangan Sudut Dalam Bersebrangan : 1 m 2 3 3 dan 4 6 5 7 8 l 6 5

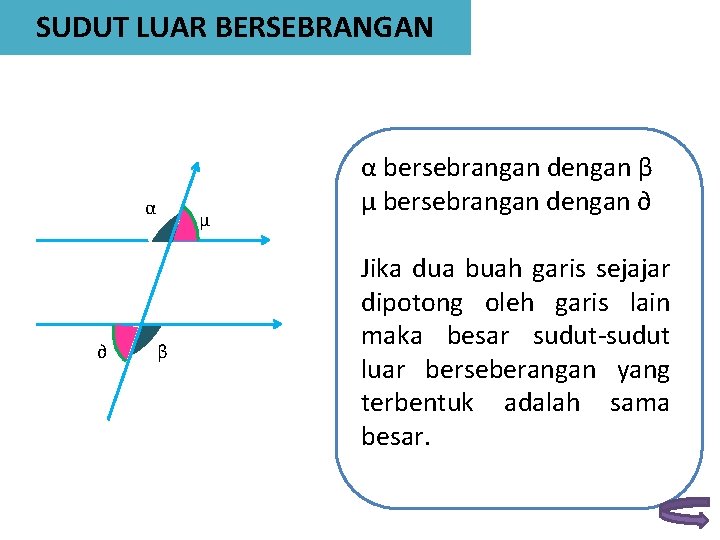
SUDUT LUAR BERSEBRANGAN α ∂ µ β α bersebrangan dengan β µ bersebrangan dengan ∂ Jika dua buah garis sejajar dipotong oleh garis lain maka besar sudut-sudut luar berseberangan yang terbentuk adalah sama besar.

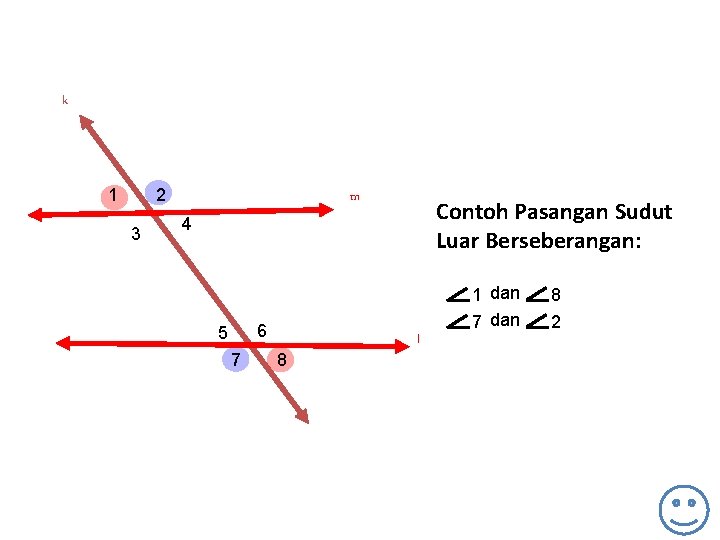
k 1 2 3 m Contoh Pasangan Sudut Luar Berseberangan: 4 6 5 7 8 l 1 dan 7 dan 8 2

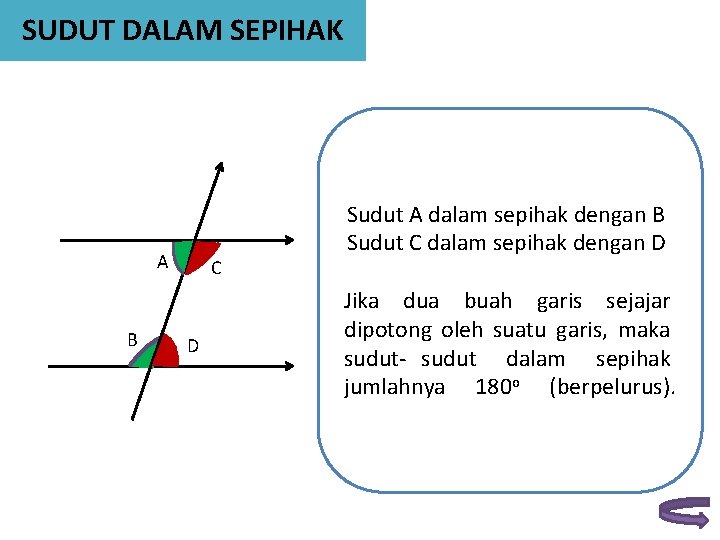
SUDUT DALAM SEPIHAK A B C D Sudut A dalam sepihak dengan B Sudut C dalam sepihak dengan D Jika dua buah garis sejajar dipotong oleh suatu garis, maka sudut- sudut dalam sepihak jumlahnya 180 o (berpelurus).

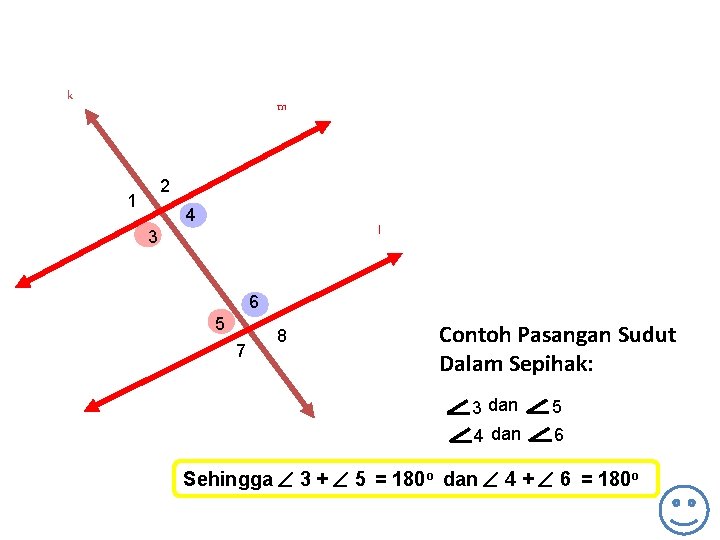
k m 2 1 4 l 3 6 5 7 8 Contoh Pasangan Sudut Dalam Sepihak: 3 dan 4 dan 5 6 Sehingga 3 + 5 = 180 o dan 4 + 6 = 180 o

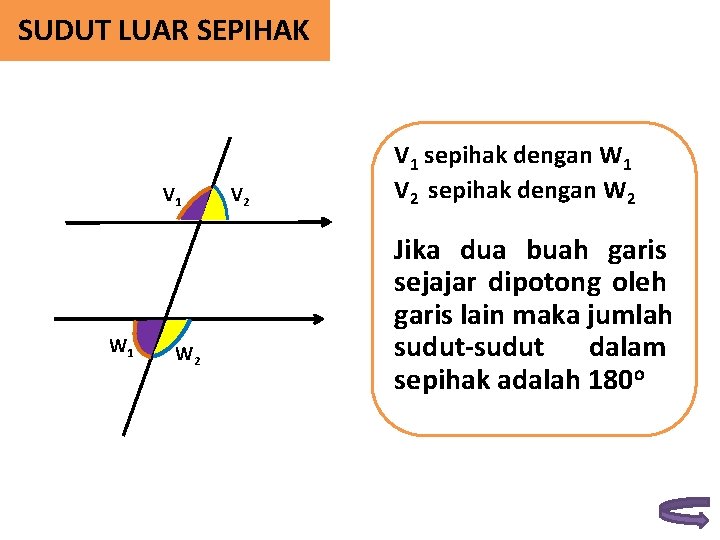
SUDUT LUAR SEPIHAK V 1 W 2 V 1 sepihak dengan W 1 V 2 sepihak dengan W 2 Jika dua buah garis sejajar dipotong oleh garis lain maka jumlah sudut-sudut dalam sepihak adalah 180 o

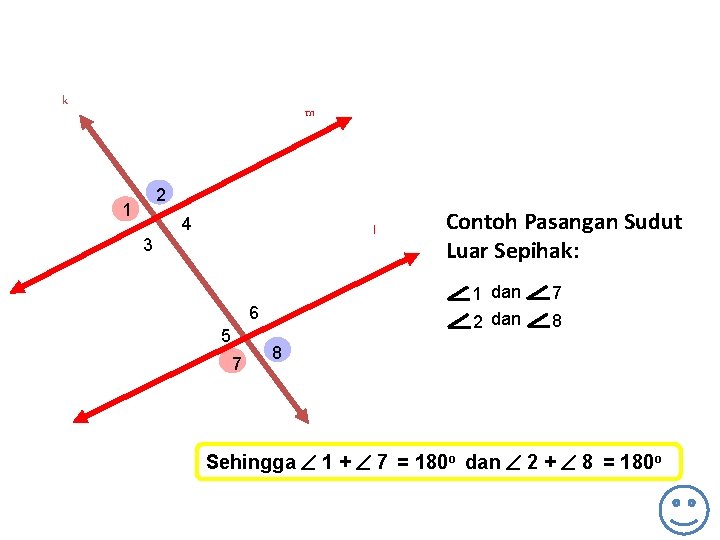
k m 2 1 4 l 3 1 dan 2 dan 6 5 7 Contoh Pasangan Sudut Luar Sepihak: 7 8 8 Sehingga 1 + 7 = 180 o dan 2 + 8 = 180 o

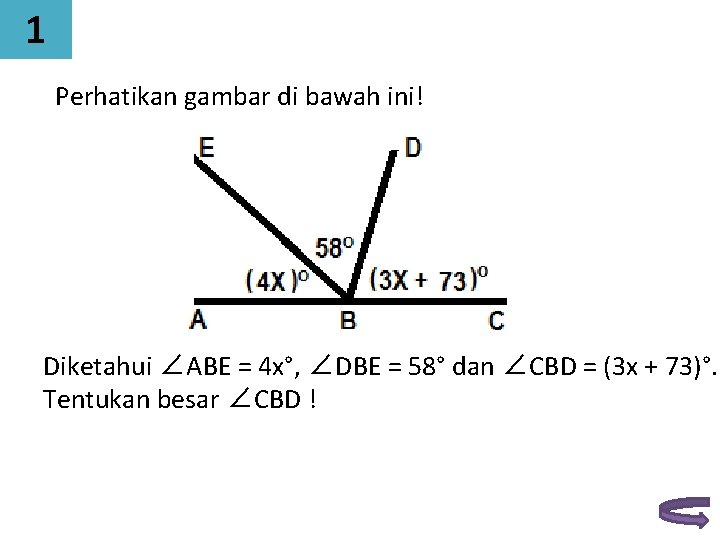
1 Perhatikan gambar di bawah ini! Diketahui ∠ABE = 4 x°, ∠DBE = 58° dan ∠CBD = (3 x + 73)°. Tentukan besar ∠CBD !

Penyelesaian: ∠ABE + ∠DBE + ∠CBD = 180° (sudut saling pelurus) 4 x°+ 58° + (3 x + 73)° = 180° 7 x°+ 131° = 180° 7 x° = 180° - 131° 7 x° = 49° x° = 7° Substitusi nilai x maka: ∠CBD = (3 x + 73)° ∠CBD = (3. 7 + 73)° ∠CBD = (21 + 73)° ∠CBD = 94°

2 Perhatikan gambar di bawah ini! Jika ukuran ∠EBF = (6 x-2)°, ukuran ∠DBE = (5 x+11)° dan ukuran ∠CBD = (7 x + 9)°, tentukan ukuran ∠DBE !

Penyelesaian: Nilai x dapat dicari dengan konsep sudut saling berpenyiku: ∠EBF + ∠DBE + ∠CBD = 90° (6 x-2)° + (5 x+11)° + (7 x + 9)° = 90° 18 x° + 18° = 180° 18 x° = 72° x = 4 ukuran ∠DBE: ∠DBE = (5 x+11)° ∠DBE = (5. 4+11)° ∠DBE = 31°

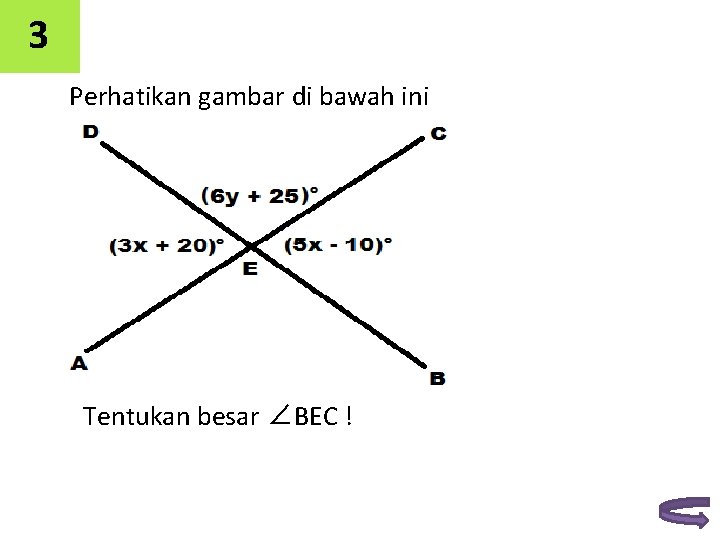
3 Perhatikan gambar di bawah ini Tentukan besar ∠BEC !

Penyelesaian: Sudut AED dan sudut BEC merupakan sudut saling bertolak belakang, maka: ∠AED = ∠BEC 5 x – 10 = 3 x + 20 5 x – 3 x = 20 + 10 2 x = 30 x = 15 Substitusi nilai x maka: ∠BEC = (3 x + 20)° ∠BEC = (3. 15 + 20)° ∠BEC = 65°

4 Perhatikan gambar di bawah ini! Tentukan nilai y !