Regression Techniques for Performance Parameter Estimation Murray Woodside

Regression Techniques for Performance Parameter Estimation Murray Woodside Carleton University Ottawa, Canada A tutorial for the WOSP/SIPEW Software Performance Workshop, San Jose, Jan 28 2010 1

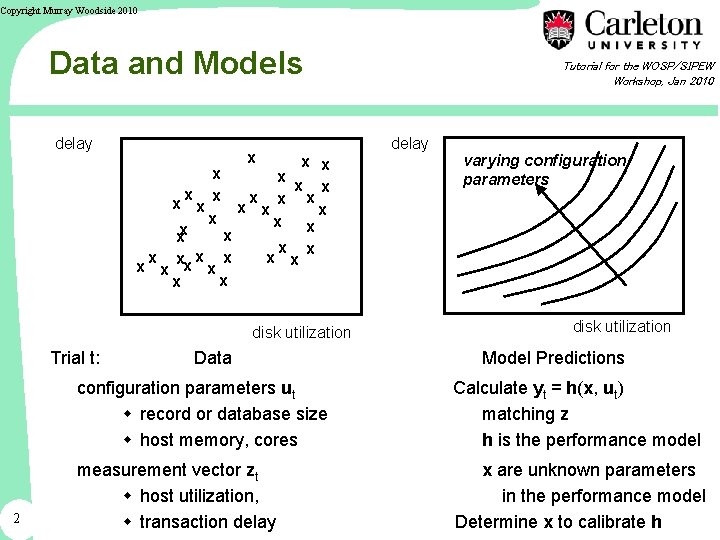
Copyright Murray Woodside 2010 Data and Models delay x x x x x xx x x x disk utilization Trial t: 2 Data Tutorial for the WOSP/SIPEW Workshop, Jan 2010 delay varying configuration parameters disk utilization Model Predictions configuration parameters ut w record or database size w host memory, cores Calculate yt = h(x, ut) matching z h is the performance model measurement vector zt w host utilization, w transaction delay x are unknown parameters in the performance model Determine x to calibrate h

Copyright Murray Woodside 2010 What is this in aid of? Tutorial for the WOSP/SIPEW Workshop, Jan 2010 1. Performance engineering is in trouble. . . ● time and effort, capability to predict over configurations 2. Models can help in interpreting data ● compact summary ● extrapolation (based on performance semantics of h) ● configuration, re-architect, re-design 3. Models created from system understanding need to be calibrated from data 4. An integrated methodology is possible ● paper “Future of Software Performance Engineering”, ICSE 2008 3

Copyright Murray Woodside 2010 Fact: model and measurement experts do not interact much Tutorial for the WOSP/SIPEW Workshop, Jan 2010 We have two solitudes, each in its own bubble Performance Measurement • tracing • profiling • instrumenting • testing • load testing • comparing 4 Performance Modeling • scenario analysis • high-level models • model generation • sensitivity • scalability • exploration of options

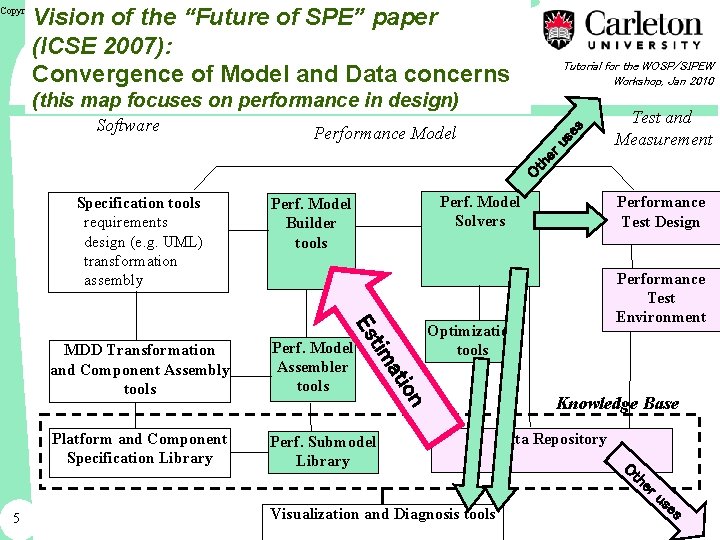
Vision of the “Future of SPE” paper (ICSE 2007): Convergence of Model and Data concerns Copyright Murray Woodside 2010 Tutorial for the WOSP/SIPEW Workshop, Jan 2010 (this map focuses on performance in design) ru se s Performance Model Test and Measurement Ot he Software Specification tools requirements design (e. g. UML) transformation assembly Es MDD Transformation and Component Assembly tools Perf. Model Assembler tools Platform and Component Specification Library Perf. Submodel Library Performance Test Design Performance Test Environment Optimization tools on ati tim 5 Perf. Model Solvers Perf. Model Builder tools Visualization and Diagnosis tools Knowledge Base Data Repository Ot he ru se s

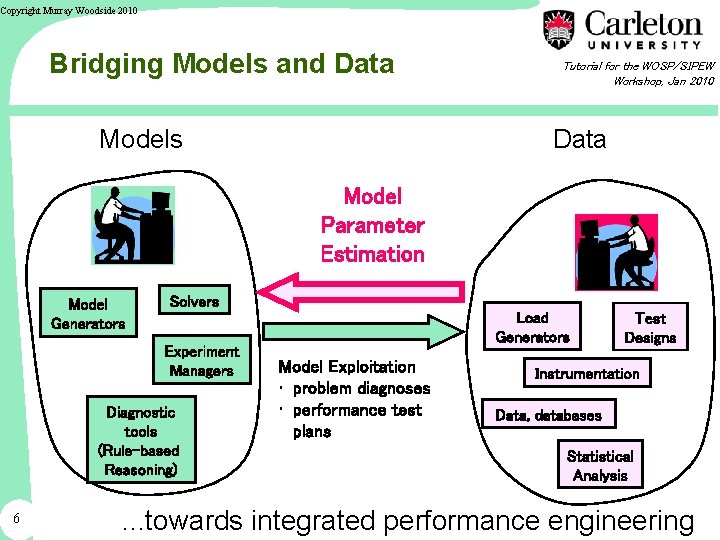
Copyright Murray Woodside 2010 Bridging Models and Data Models Tutorial for the WOSP/SIPEW Workshop, Jan 2010 Data Model Parameter Estimation Model Generators Solvers Experiment Managers Diagnostic tools (Rule-based Reasoning) 6 Load Generators Model Exploitation • problem diagnoses • performance test plans Test Designs Instrumentation Data, databases Statistical Analysis . . . towards integrated performance engineering

Copyright Murray Woodside 2010 Starting Point Tutorial for the WOSP/SIPEW Workshop, Jan 2010 ● What kind of measurements? ● Where do models come from? § measurements here averages over a test period § multiple variables are averaged over the same period § models can come from w a basic recipe (e. g. , a set of queue servers) w the system configuration w software analysis (e. g. UML annotated by MARTE) w modeling expertise is pretty important. . . § simplest is best § curve-fit models (not performance models) will be 7 discussed later

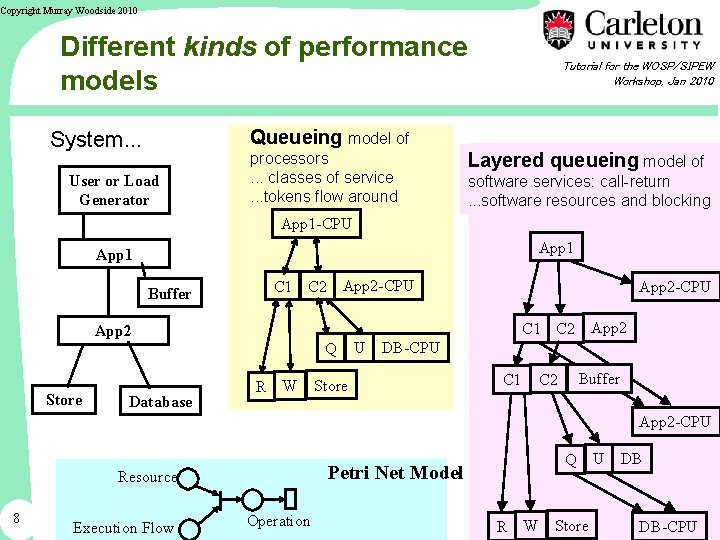
Copyright Murray Woodside 2010 Different kinds of performance models Tutorial for the WOSP/SIPEW Workshop, Jan 2010 Queueing model of System. . . User or Load Generator processors. . . classes of service. . . tokens flow around Layered queueing model of software services: call-return. . . software resources and blocking App 1 -CPU App 1 Buffer Database App 2 -CPU App 2 C 1 C 2 App 2 Store App 2 -CPU C 1 C 2 Q R W U DB-CPU Store C 1 Buffer C 2 App 2 -CPU Petri Net Model Resource 8 Execution Flow Q Operation R W Store U DB DB-CPU

Copyright Murray Woodside 2010 Example. . Automation of performance modeling from annotated UML PUMA Cycle ● annotate the UML spec (new standard profile MARTE), ● generate the Performance Model ● many examples ● e. g. PUMA (Perf. by Unified Model Analysis) (paper in WOSP 2005) 9 Tutorial for the WOSP/SIPEW Workshop, Jan 2010

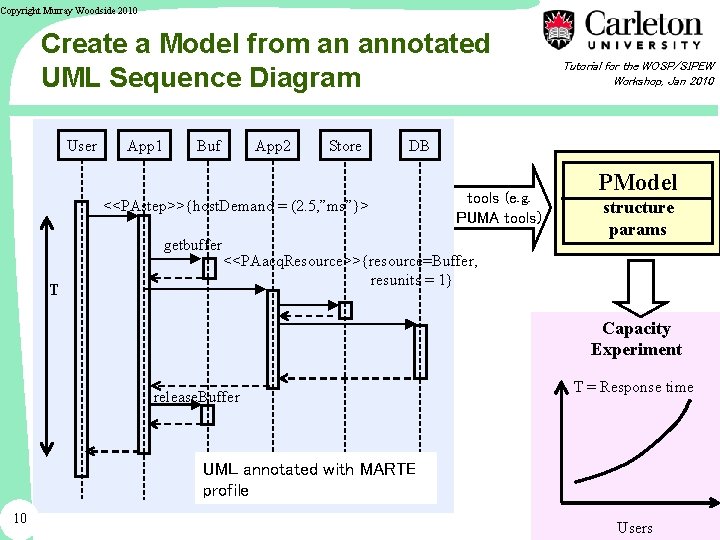
Copyright Murray Woodside 2010 Create a Model from an annotated UML Sequence Diagram User App 1 Buf App 2 Store DB <<PAstep>>{host. Demand = (2. 5, ”ms”}> getbuffer T Tutorial for the WOSP/SIPEW Workshop, Jan 2010 tools (e. g. PUMA tools) PModel structure params <<PAacq. Resource>>{resource=Buffer, resunits = 1} Capacity Experiment release. Buffer T = Response time UML annotated with MARTE profile 10 Users

Copyright Murray Woodside 2010 View of the Performance Model h(x, u) ● h can be any performance model § queueing, layered queueing, petri net, etc § special challenge for simulation models (later) Tutorial for the WOSP/SIPEW Workshop, Jan 2010 h ● x contains the unknown parameter values ● u contains known parameters that vary from test to test § e. g. the number of users, or the arrival rate § assumption that x does not depend on u (discuss later) 11 ● Sensitivity matrix H(x; ut) = h(x; ut)/ x is important § Hij(x; ut) = hi(x; ut)/ xj u

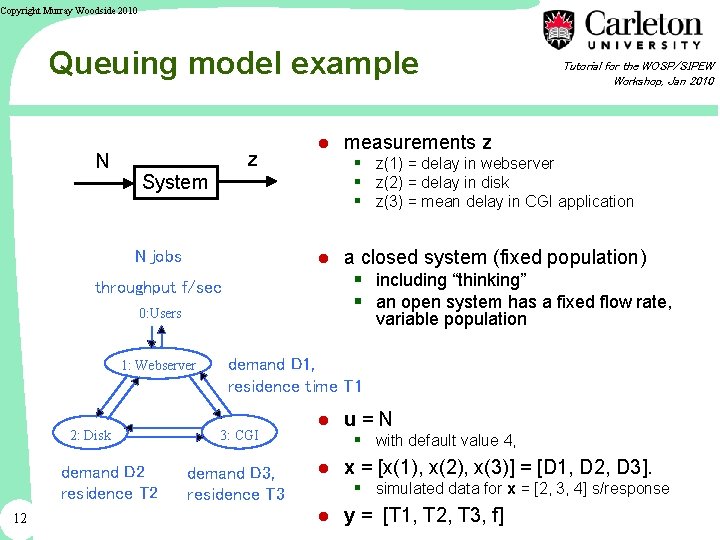
Copyright Murray Woodside 2010 Queuing model example N z System throughput f/sec 0: Users 12 § z(1) = delay in webserver § z(2) = delay in disk § z(3) = mean delay in CGI application variable population 1: Webserver demand D 2 residence T 2 ● measurements z ● a closed system (fixed population) § including “thinking” § an open system has a fixed flow rate, N jobs 2: Disk Tutorial for the WOSP/SIPEW Workshop, Jan 2010 demand D 1, residence time T 1 3: CGI demand D 3, residence T 3 ● u=N § with default value 4, ● x = [x(1), x(2), x(3)] = [D 1, D 2, D 3]. § simulated data for x = [2, 3, 4] s/response ● y = [T 1, T 2, T 3, f]

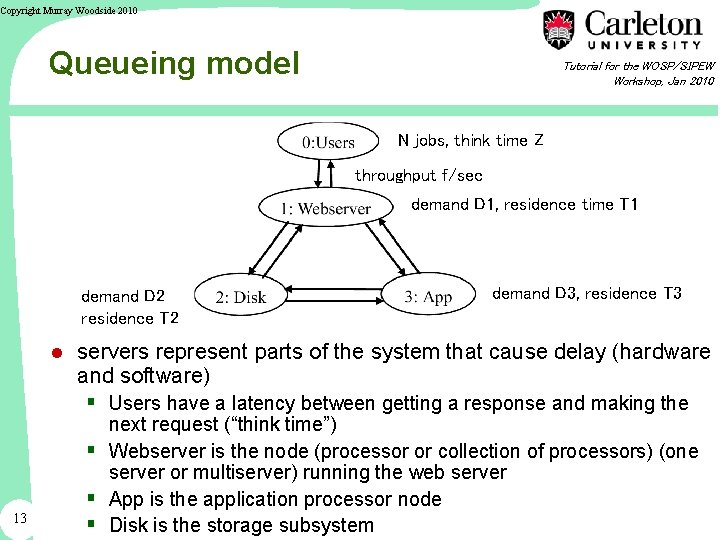
Copyright Murray Woodside 2010 Queueing model Tutorial for the WOSP/SIPEW Workshop, Jan 2010 N jobs, think time Z throughput f/sec demand D 1, residence time T 1 demand D 2 residence T 2 demand D 3, residence T 3 ● servers represent parts of the system that cause delay (hardware and software) § Users have a latency between getting a response and making the 13 next request (“think time”) § Webserver is the node (processor or collection of processors) (one server or multiserver) running the web server § App is the application processor node § Disk is the storage subsystem

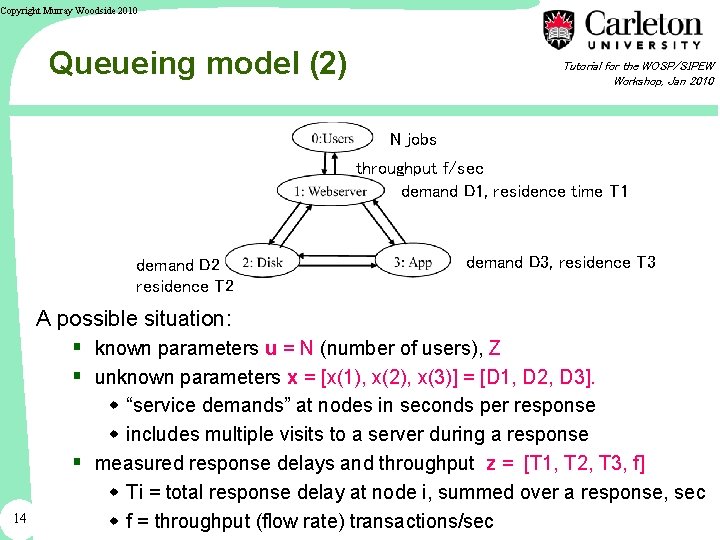
Copyright Murray Woodside 2010 Queueing model (2) Tutorial for the WOSP/SIPEW Workshop, Jan 2010 N jobs throughput f/sec demand D 1, residence time T 1 demand D 2 residence T 2 demand D 3, residence T 3 A possible situation: § known parameters u = N (number of users), Z § unknown parameters x = [x(1), x(2), x(3)] = [D 1, D 2, D 3]. 14 w “service demands” at nodes in seconds per response w includes multiple visits to a server during a response § measured response delays and throughput z = [T 1, T 2, T 3, f] w Ti = total response delay at node i, summed over a response, sec w f = throughput (flow rate) transactions/sec

Copyright Murray Woodside 2010 Regression: fit and error Tutorial for the WOSP/SIPEW Workshop, Jan 2010 ● measurement = steady-state value + meas’t error § (measurement error comes from averaging over a finite test duration = sampling error) § sampling error is approx normally distributed w variance ~ 1/S, for sample size S ● for test number “t” (t = 1, 2, . . ) zt = h(x, ut) + approximation error + measurement error § regression assumes the sum of the two errors is normal ● zt = h(x, ut) + vt § v is assumed to have constant covariance over t 15

Copyright Murray Woodside 2010 Regression formulation Tutorial for the WOSP/SIPEW Workshop, Jan 2010 ● minx E(x) = St (yt − zt)2 (scalar y= h(x, u) and z) E(x) = St (yt − zt)TR-1(yt − zt) (vector y = h(x, u) and z) ● Diagonal weight matrix R reflects the relative variances for different measurements in z § called “generalized” least squares § z = h(x, u) + v § Rjj ~ variance of vj 16

Copyright Murray Woodside 2010 We will need a linearization of h( ) Tutorial for the WOSP/SIPEW Workshop, Jan 2010 ● Regression needs a linear relationship ● The sensitivity matrix H = h(x, u)/ x is central h 1/ x 1 h 1/ x 2. . . H(x, u) = . . . h 1/ xn h 2/ x 1 h 2/ x 2. . . hm/ x 1 hm/ x 2. . . ● for x near a point x*, h(x, u) = h(x*, u) + H(x*, u)(x – x*) + higher terms 17 (Taylor series)

Copyright Murray Woodside 2010 Gradient solution to Min E Tutorial for the WOSP/SIPEW Workshop, Jan 2010 An example of an ad hoc numerical minimization approach ● E(x) = St (yt − zt)TR-1(yt − zt) = St e. TR-1 e et = (yt − zt) Iterative solution from some starting x ● The gradient vector of E is E(x)/ x = − 2 St HT(x; ut) R-1 et 18 § gradient step is: new x = old x - (step parameter)* E(x)/ x

Copyright Murray Woodside 2010 Approximate Newton Raphson iteration Tutorial for the WOSP/SIPEW Workshop, Jan 2010 ● A second-order approximation to E(x) is E(x* + Dx) = E(x*) + Ex Dx + ½ Dx. T Exx Dx + higher terms ● A Newton-Raphson step to minimize E is 19 new x = x* + Dx = x* - Exx-1 Ex where Ex = E(x)/ x = − 2 St HT(x; ut) R-1 et, Exx = 2 E(x)/ x 2 = − 2 St HT(x; ut)/ x R-1 e +2 St H(x; ut)TR-1 H(x; ut) ≈ 2 St H(x; ut)T R-1 H(x; ut) (the first term is hard to compute and is small as e → 0)

Copyright Murray Woodside 2010 Approximate Newton-Raphson (2) Tutorial for the WOSP/SIPEW Workshop, Jan 2010 This can also be seen as successive linear regressions: 1. At the current estimate x, find the best increment Dx by fitting the Taylor expansion to h for each t, using H: 2. zt = h(x; ut) + H(x; ut)(Dx) + higher terms + vt 3. formulate the linear regression problem to find Dx, min. Dx E(x + Dx) = St (h(x + Dx, ut) − zt)TR-1(h(x + Dx, ut) − zt) 4. solve as before, but with Dx taking the role of x and H(x, ut) taking the role of B: 5. 20 Dx = (St H(x, ut)TR-1 H(x, ut))-1 (St H(x, ut)TR-1 zt) 6. replace x by x + Dx, repeat to convergence

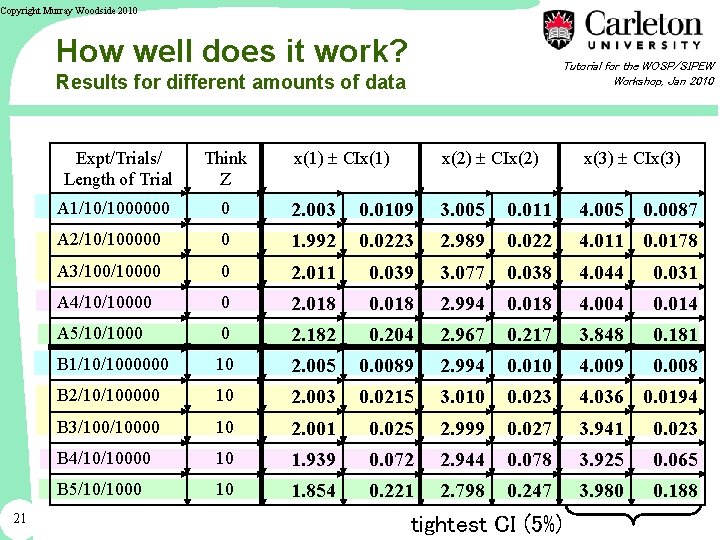
Copyright Murray Woodside 2010 How well does it work? Tutorial for the WOSP/SIPEW Workshop, Jan 2010 Results for different amounts of data 21 x(1) CIx(1) x(2) CIx(2) x(3) CIx(3) 0 2. 003 0. 0109 3. 005 0. 011 4. 005 0. 0087 A 2/10/100000 0 1. 992 0. 0223 2. 989 0. 022 4. 011 0. 0178 A 3/10000 0 2. 011 0. 039 3. 077 0. 038 4. 044 0. 031 A 4/10/10000 0 2. 018 0. 018 2. 994 0. 018 4. 004 0. 014 A 5/10/1000 0 2. 182 0. 204 2. 967 0. 217 3. 848 0. 181 B 1/10/1000000 10 2. 005 0. 0089 2. 994 0. 010 4. 009 0. 008 B 2/10/100000 10 2. 003 0. 0215 3. 010 0. 023 4. 036 0. 0194 B 3/10000 10 2. 001 0. 025 2. 999 0. 027 3. 941 0. 023 B 4/10/10000 10 1. 939 0. 072 2. 944 0. 078 3. 925 0. 065 B 5/10/1000 10 1. 854 0. 221 2. 798 0. 247 3. 980 0. 188 Expt/Trials/ Length of Trial Think Z A 1/10/1000000 tightest CI (5%)

Copyright Murray Woodside 2010 How to find confidence intervals Tutorial for the WOSP/SIPEW Workshop, Jan 2010 ● Standard regression methods are used to produce confidence intervals (CI) for x § based on each iteration being a linear regression for Dx § the CI is for Dx at convergence ● Actually first a covariance matrix P for Dx is calculated: P = (mse) (St Ht. TR-1 Ht)-1 § where mse is an estimator for goodness of fit, given by mse = (St et. TR-1 et )/(m. T n) 22 w m = dimension of y and z w T = number of time points for data w n = dimension of x w m. T – n is the number of degrees of freedom (data – parameters)

Copyright Murray Woodside 2010 Confidence intervals: correlation Tutorial for the WOSP/SIPEW Workshop, Jan 2010 The Dx are in general correlated, as given by off-diagonal elements of P, so their confidence intervals are not independent § under the assumptions of linearity and normally distributed errors of measurement, Dx are also normal § in 2 dimensions the confidence region is an ellipse, § bounded by a contour of the distribution of Dx x 23 Our CI’s are based on the marginal distributions point estimate of (x 1, x 2) 95% of probability

Copyright Murray Woodside 2010 Confidence intervals: Math Tutorial for the WOSP/SIPEW Workshop, Jan 2010 ● For simplicity we can base independent CIs on the marginal variances found for each Dxi § estimated variance is Pii § this will be conservative ● CI for xi at confidence level a is then xi t(1 -a/2; m. T-n) (sqrt(Pii )) § where t(1 -a/2; m. T-n) is a tabulated t-statistic § for a = 0. 95 and large m. T-n, t( ) → 1. 96 24

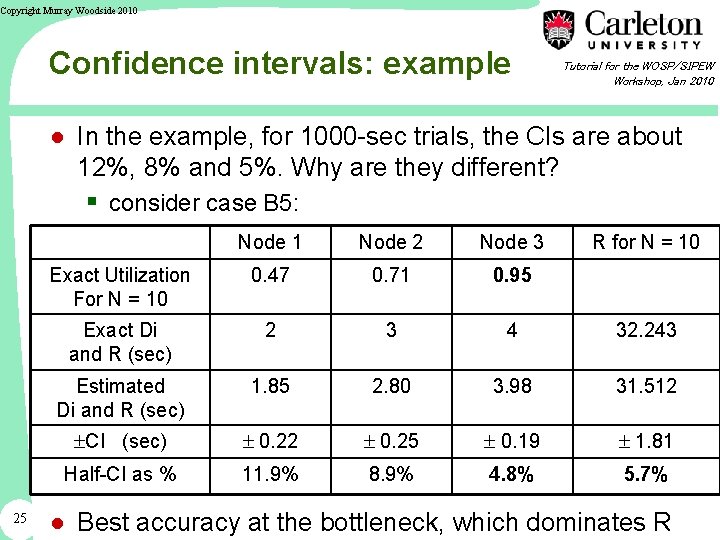
Copyright Murray Woodside 2010 Confidence intervals: example Tutorial for the WOSP/SIPEW Workshop, Jan 2010 ● In the example, for 1000 -sec trials, the CIs are about 12%, 8% and 5%. Why are they different? § consider case B 5: 25 Node 1 Node 2 Node 3 R for N = 10 Exact Utilization For N = 10 0. 47 0. 71 0. 95 Exact Di and R (sec) 2 3 4 32. 243 Estimated Di and R (sec) 1. 85 2. 80 3. 98 31. 512 CI (sec) 0. 22 0. 25 0. 19 1. 81 Half-CI as % 11. 9% 8. 9% 4. 8% 5. 7% ● Best accuracy at the bottleneck, which dominates R

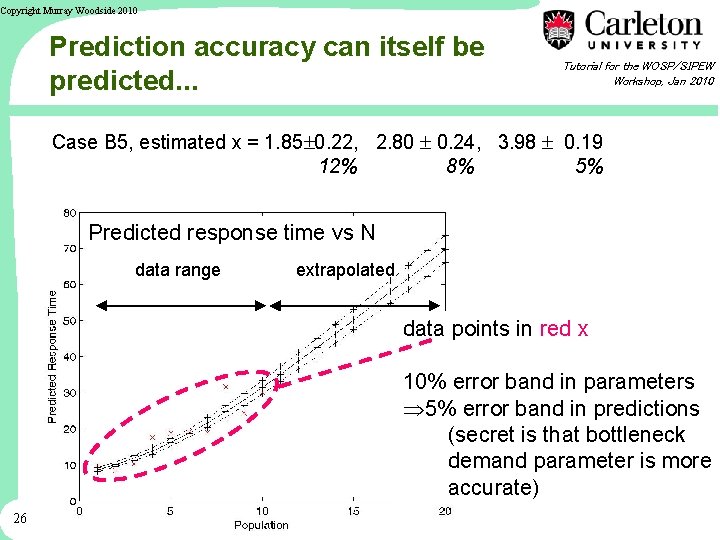
Copyright Murray Woodside 2010 Prediction accuracy can itself be predicted. . . Tutorial for the WOSP/SIPEW Workshop, Jan 2010 Case B 5, estimated x = 1. 85 0. 22, 2. 80 0. 24, 3. 98 0. 19 12% 8% 5% Predicted response time vs N data range extrapolated data points in red x 10% error band in parameters Þ 5% error band in predictions (secret is that bottleneck demand parameter is more accurate) 26

Copyright Murray Woodside 2010 Prediction accuracy calculation Tutorial for the WOSP/SIPEW Workshop, Jan 2010 1. near the estimate x cov(Dx) = P 2. also Dy = H(x, u) Dx 3. so C = Cov(y) = Cov(Dy) (since covariance is around the mean) = H(x, u) P HT(x, u) 4. standard deviation for Dyi is sqrt(Cii), so 27 CI for yi is: yi t(1 -a/2; m. T-n) (sqrt(Cii ))

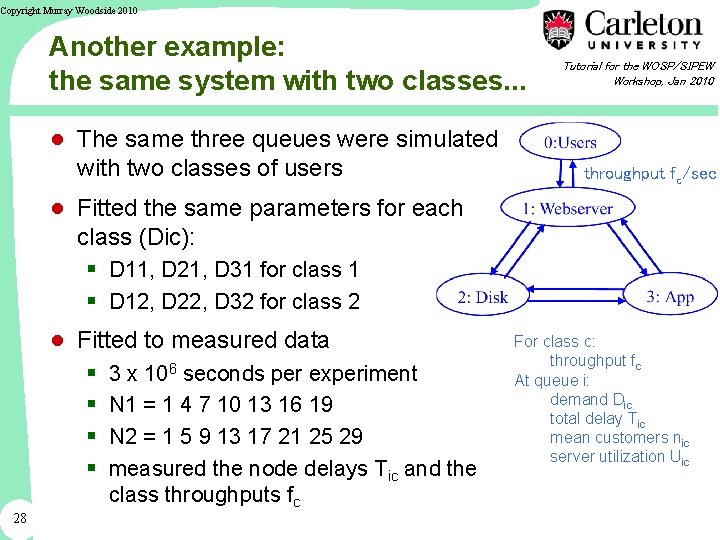
Copyright Murray Woodside 2010 Another example: the same system with two classes. . . ● The same three queues were simulated with two classes of users Tutorial for the WOSP/SIPEW Workshop, Jan 2010 throughput fc/sec ● Fitted the same parameters for each class (Dic): § D 11, D 21, D 31 for class 1 § D 12, D 22, D 32 for class 2 ● Fitted to measured data § 3 x 106 seconds per experiment § N 1 = 1 4 7 10 13 16 19 § N 2 = 1 5 9 13 17 21 25 29 § measured the node delays Tic and the 28 class throughputs fc For class c: throughput fc At queue i: demand Dic total delay Tic mean customers nic server utilization Uic

Copyright Murray Woodside 2010 Results with two classes. . . Tutorial for the WOSP/SIPEW Workshop, Jan 2010 ● Results were similar This was for 56 data points, each based on 30 blocks of 100000 sec D 11 Sim: Fit: 2 2. 000 D 21 D 31 3 4 Z 1 D 12 10 5 D 32 Z 2 10 1 30 3. 018 4. 033 5. 001 9. 968 1. 026 CI 95: . 008 . 003 . 012 . 009 . 003 . 5% . 1% . 2% . 1% . 3% throughput f/sec 29 D 22 For class c: throughput fc At queue i: demand Dic total delay Tic mean customers nic server utilization Uic

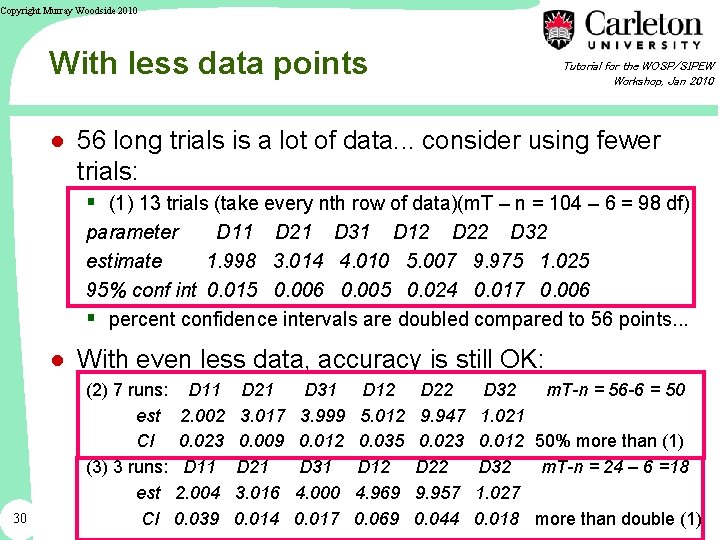
Copyright Murray Woodside 2010 With less data points Tutorial for the WOSP/SIPEW Workshop, Jan 2010 ● 56 long trials is a lot of data. . . consider using fewer trials: § (1) 13 trials (take every nth row of data)(m. T – n = 104 – 6 = 98 df) parameter D 11 D 21 D 31 D 12 D 22 D 32 estimate 1. 998 3. 014 4. 010 5. 007 9. 975 1. 025 95% conf int 0. 015 0. 006 0. 005 0. 024 0. 017 0. 006 § percent confidence intervals are doubled compared to 56 points. . . ● With even less data, accuracy is still OK: 30 (2) 7 runs: est CI (3) 3 runs: est CI D 11 2. 002 0. 023 D 11 2. 004 0. 039 D 21 3. 017 0. 009 D 21 3. 016 0. 014 D 31 3. 999 0. 012 D 31 4. 000 0. 017 D 12 5. 012 0. 035 D 12 4. 969 0. 069 D 22 9. 947 0. 023 D 22 9. 957 0. 044 D 32 m. T-n = 56 -6 = 50 1. 021 0. 012 50% more than (1) D 32 m. T-n = 24 – 6 =18 1. 027 0. 018 more than double (1)

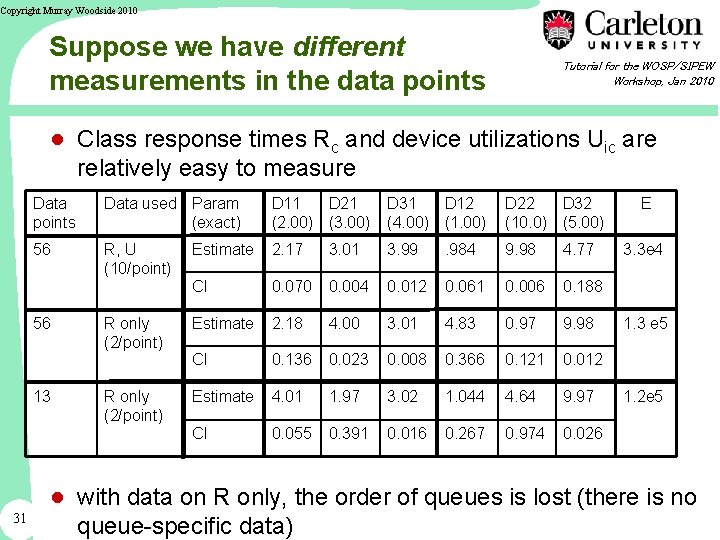
Copyright Murray Woodside 2010 Suppose we have different measurements in the data points Tutorial for the WOSP/SIPEW Workshop, Jan 2010 ● Class response times Rc and device utilizations Uic are relatively easy to measure Data points Data used Param (exact) D 11 D 21 (2. 00) (3. 00) D 31 D 12 (4. 00) (1. 00) D 22 D 32 (10. 0) (5. 00) 56 R, U (10/point) Estimate 2. 17 3. 01 3. 99 . 984 9. 98 4. 77 CI 0. 070 0. 004 0. 012 0. 061 0. 006 0. 188 R only (2/point) Estimate 2. 18 4. 00 3. 01 4. 83 0. 97 9. 98 CI 0. 136 0. 023 0. 008 0. 366 0. 121 0. 012 R only (2/point) Estimate 4. 01 1. 97 3. 02 1. 044 4. 64 9. 97 CI 0. 055 0. 391 0. 016 0. 267 0. 974 0. 026 56 13 31 E 3. 3 e 4 1. 3 e 5 1. 2 e 5 ● with data on R only, the order of queues is lost (there is no queue-specific data)

Copyright Murray Woodside 2010 Observations on fitting queuing models Tutorial for the WOSP/SIPEW Workshop, Jan 2010 1. Always fit a constant (a think time) to a delay measurement ● a latency term in the delay ● it stands for system elements missing in the model 2. Many systems have a dominant bottleneck resource w they behave rather like a single queue plus a latency w The latency stands for delays at all the other resources w to obtain good estimates for the other resources include data in the non-bottleneck region include data about those resources (e. g. , their utilization) 32

Copyright Murray Woodside 2010 Observations (2) Tutorial for the WOSP/SIPEW Workshop, Jan 2010 3. Other queuing models can be used § more queues, or fewer § each model produces a goodness of fit E § you can test the models for significance (a significant reduction in E) w “did the extra parameter produce enough reduction” § you can also examine the confidence intervals w models with too much detail tend to give large intervals on some or all parameters w the parameters can substitute for each other 33

Copyright Murray Woodside 2010 Significance testing for model structure Tutorial for the WOSP/SIPEW Workshop, Jan 2010 ● To tell if you have the right model structure § call the model m 1, its number of fitted parameters n 1, and its goodness of fit, E 1 = St e. TR-1 e § another model m 2 with n 2 parameters has fit E 2 ● is m 1 significantly better than m 2? § this requires an F-test: w m 1 is better than m 2 at level a if: w F-statistic > critical F-value (tabulated) at level a w for 95% probability it is better, a = 0. 05 [(E 2−E 1)/(n 1−n 2)]/[E 2/(m. T−n 2− 1)] > F(n 2−n 1, m. T−n − 1, a) 34

Copyright Murray Woodside 2010 Significance vs a simpler 2 -queue model, on data for 3 queues Tutorial for the WOSP/SIPEW Workshop, Jan 2010 ● m 1 has three queues with E 1 = 32. 9, n 1 = 6, m = 8, T = 56 D 11 Sim: Fit: 2 2. 000 CI 95: . 008 D 12 D 13 D 21 D 22 D 23 3 4 5 10 1 3. 018 4. 033 5. 001 9. 968 1. 026. 003 . 012 . 009 . 003 ● m 2 has two queues with E 2 = 4034, n 2 = 4, m = 6, T = 56 D 11 D 12 D 21 D 22 2. 13 3. 24 4. 88 9. 68. . for class 2 it has “chosen” queue 1, 2 CI 95: . 087 . 038 . 144 . 107. . about 10 times as big Fit: ● F = [(E 2−E 1)/(n 2−n 1)]/[E 2/(m. T−n 2− 1)] = [(4034− 33)/(6− 4)]/[4034/(448− 6− 1)] = 220. 4 35 ● tabulated F(2, 441, . 05) = 19. 5. . so, m 1 is better.

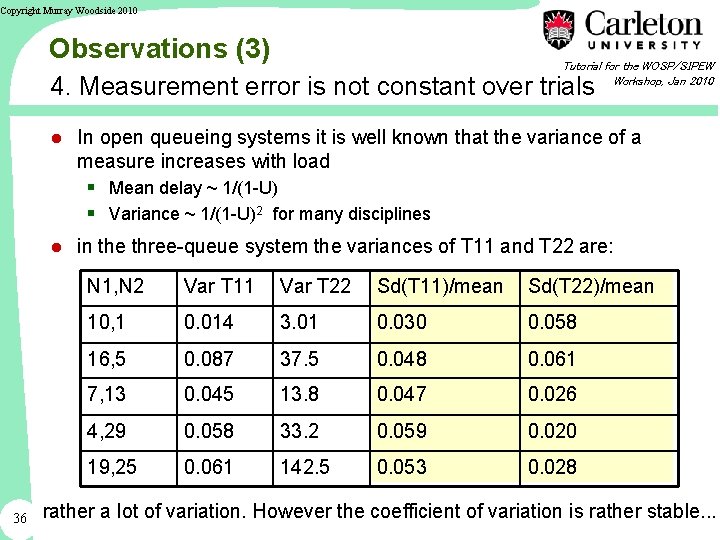
Copyright Murray Woodside 2010 Observations (3) Tutorial for the WOSP/SIPEW Workshop, Jan 2010 4. Measurement error is not constant over trials ● In open queueing systems it is well known that the variance of a measure increases with load § Mean delay ~ 1/(1 -U) § Variance ~ 1/(1 -U)2 for many disciplines ● in the three-queue system the variances of T 11 and T 22 are: N 1, N 2 Var T 11 Var T 22 Sd(T 11)/mean Sd(T 22)/mean 10, 1 0. 014 3. 01 0. 030 0. 058 16, 5 0. 087 37. 5 0. 048 0. 061 7, 13 0. 045 13. 8 0. 047 0. 026 4, 29 0. 058 33. 2 0. 059 0. 020 19, 25 0. 061 142. 5 0. 053 0. 028 So, 36 rather a lot of variation. However the coefficient of variation is rather stable. . .

Copyright Murray Woodside 2010 Dealing with varying measurement errors Tutorial for the WOSP/SIPEW Workshop, Jan 2010 ● The weight matrix W = R-1 can be a function of the sample t, provided it is known. Then § min E(x) = St (yt − zt)TWt(yt − zt) ● only ad hoc approaches are available, § i. e. if we think the coefficient of variation is constant, we could set Wii, t equal to (constanti) x zit 2 ● but ignoring the variation does not seem to work too badly. . . 37

Copyright Murray Woodside 2010 Observations (4) Tutorial for the WOSP/SIPEW Workshop, Jan 2010 5. Is the violation of regression assumptions a serious issue for good fitting? ● It seems not. The key assumptions are § linear h in x § normal measurement errors with const variance § if these are true, the residuals have a multivariate normal distribution, and the fitted parameters also w shown by elliptical contours of the probability density function w and elliptical contours of E(x) centered around the fitted value of x 38

Copyright Murray Woodside 2010 Contours of E for a two-Class Model Tutorial for the WOSP/SIPEW Workshop, Jan 2010 D 2 from 2. 5 to 3. 5 in steps of 0. 025 D 1 from 9. 5 to 10. 5 in steps of 0. 05 ● If the regression approximation assumptions are satisfied § (linear h, normal error) § then E(x) is normal with estimated mean Xest, covariance matrix P. § a 2 -dimensional normal distribution has elliptical contours 39 ● Here we see that contours of E are nearly elliptical, so the assumptions are supported.

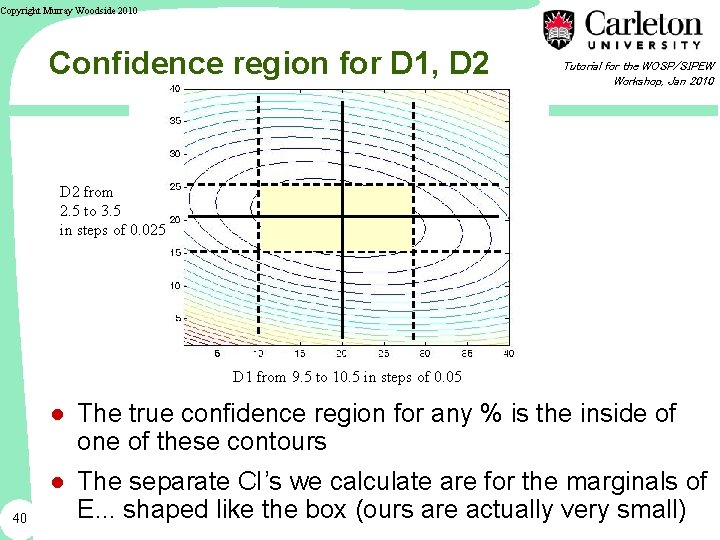
Copyright Murray Woodside 2010 Confidence region for D 1, D 2 Tutorial for the WOSP/SIPEW Workshop, Jan 2010 D 2 from 2. 5 to 3. 5 in steps of 0. 025 D 1 from 9. 5 to 10. 5 in steps of 0. 05 ● The true confidence region for any % is the inside of one of these contours 40 ● The separate CI’s we calculate are for the marginals of E. . . shaped like the box (ours are actually very small)

Copyright Murray Woodside 2010 Now consider more structured and complex models Tutorial for the WOSP/SIPEW Workshop, Jan 2010 ● Real systems have more structure to their resources, than a simple queueing model § this may or may not be important ● Extended queueing models can capture this extra structure § memory resources § process resources § etc. 41 ● Layered queues are a canonical form for extended queueing, § adapted to layered service systems § also usable on other systems, eg event-based systems

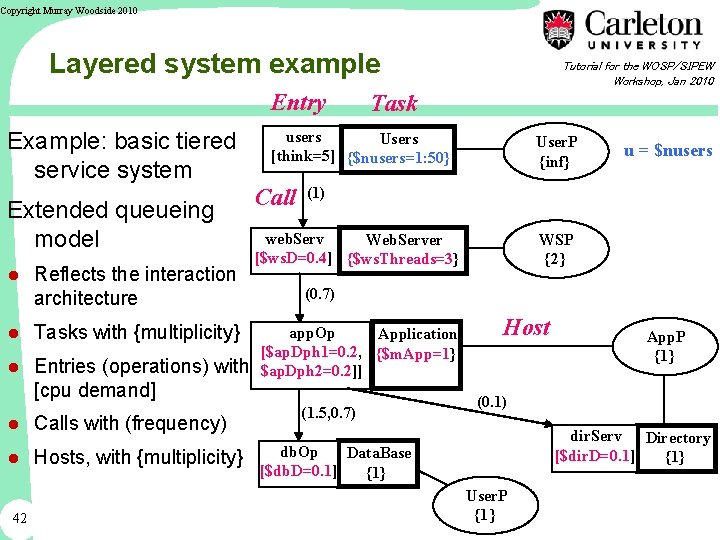
Copyright Murray Woodside 2010 Layered system example Entry Example: basic tiered service system Extended queueing model ● Reflects the interaction architecture ● Tasks with {multiplicity} ● Entries (operations) with [cpu demand] ● Calls with (frequency) ● Hosts, with {multiplicity} 42 Tutorial for the WOSP/SIPEW Workshop, Jan 2010 Task users Users [think=5] {$nusers=1: 50} Call User. P {inf} u = $nusers (1) web. Serv Web. Server [$ws. D=0. 4] {$ws. Threads=3} WSP {2} (0. 7) app. Op Application [$ap. Dph 1=0. 2, {$m. App=1} $ap. Dph 2=0. 2]] (1. 5, 0. 7) Host App. P {1} (0. 1) dir. Serv Directory [$dir. D=0. 1] {1} db. Op Data. Base [$db. D=0. 1] {1} User. P {1 }

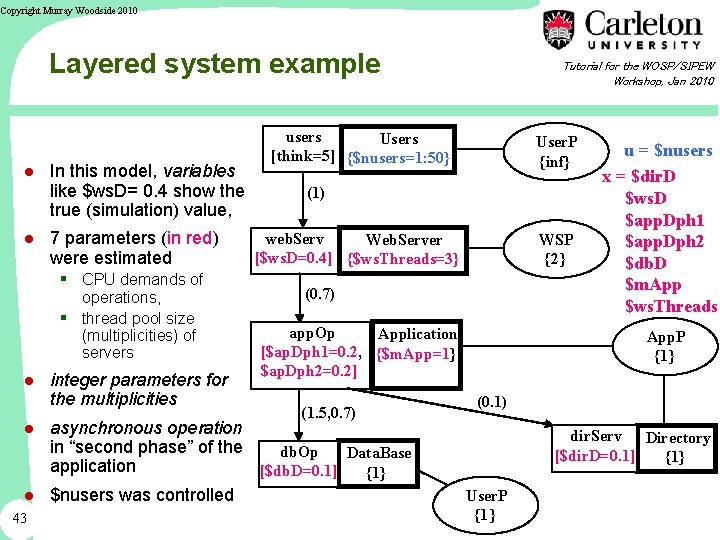
Copyright Murray Woodside 2010 Layered system example ● In this model, variables like $ws. D= 0. 4 show the true (simulation) value, ● 7 parameters (in red) were estimated § CPU demands of operations, § thread pool size (multiplicities) of servers ● integer parameters for the multiplicities users Users [think=5] {$nusers=1: 50} User. P {inf} (1) web. Serv Web. Server [$ws. D=0. 4] {$ws. Threads=3} WSP {2} (0. 7) app. Op Application [$ap. Dph 1=0. 2, {$m. App=1} $ap. Dph 2=0. 2] (1. 5, 0. 7) ● asynchronous operation in “second phase” of the db. Op Data. Base application [$db. D=0. 1] {1} ● $nusers was controlled 43 Tutorial for the WOSP/SIPEW Workshop, Jan 2010 u = $nusers x = $dir. D $ws. D $app. Dph 1 $app. Dph 2 $db. D $m. App $ws. Threads App. P {1} (0. 1) dir. Serv Directory [$dir. D=0. 1] {1} User. P {1 }

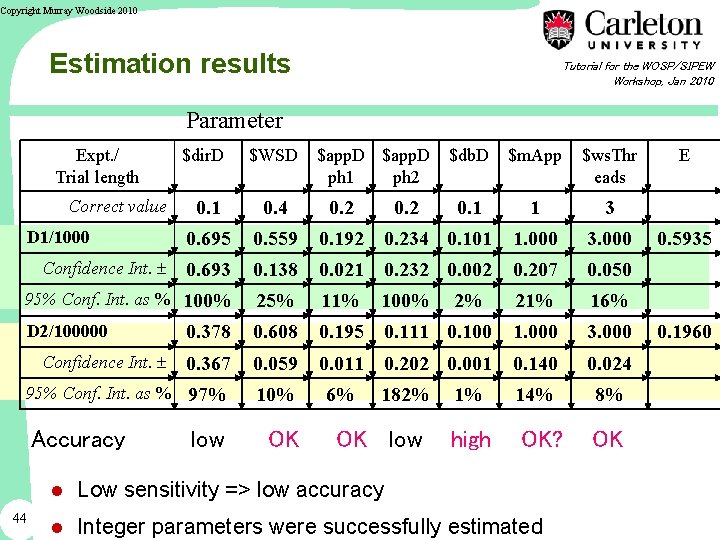
Copyright Murray Woodside 2010 Estimation results Tutorial for the WOSP/SIPEW Workshop, Jan 2010 Parameter Expt. / Trial length Correct value $dir. D $WSD $app. D ph 1 ph 2 $m. App $ws. Thr eads 0. 1 1 3 0. 1 0. 4 0. 2 0. 695 0. 559 0. 192 0. 234 0. 101 1. 000 3. 000 0. 693 0. 138 0. 021 0. 232 0. 002 0. 207 0. 050 95% Conf. Int. as % 100% 25% 11% 100% 21% 16% D 2/100000 0. 378 0. 608 0. 195 0. 111 0. 100 1. 000 3. 000 0. 367 0. 059 0. 011 0. 202 0. 001 0. 140 0. 024 95% Conf. Int. as % 97% 10% 6% 182% 1% 14% 8% high OK? OK D 1/1000 Confidence Int. Accuracy low OK 0. 2 $db. D OK low 2% ● Low sensitivity => low accuracy 44 ● Integer parameters were successfully estimated E 0. 5935 0. 1960

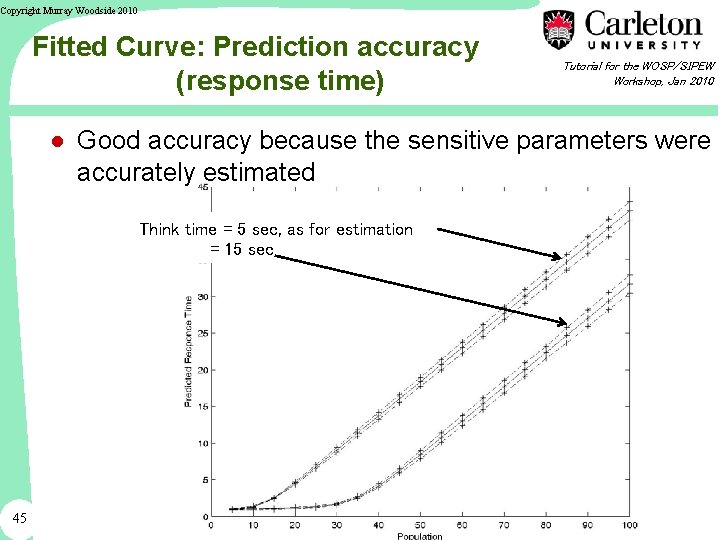
Copyright Murray Woodside 2010 Fitted Curve: Prediction accuracy (response time) Tutorial for the WOSP/SIPEW Workshop, Jan 2010 ● Good accuracy because the sensitive parameters were accurately estimated Think time = 5 sec, as for estimation = 15 sec 45

Copyright Murray Woodside 2010 How to do it Tutorial for the WOSP/SIPEW Workshop, Jan 2010 ● I have a bunch of data, how do I fit models? ● first, I need a hypothesis for a model § a think time and a set of queues will do § if it is test data with a load driver, a closed model is indicated § if it is data recorded “in the wild” with a varying load, try a closed approximation (fix a large N, and for each test set Zt = N/ft) ● with multiple measures averaged over each run, the relative variance of each must be estimated for R § roughly. The simplest assumption is equal variances ● set initial values and iterate. I use MATLAB. . . § The model calculation h(x) is done by a function § The sensitivity matrix H is computed by finite differences § For integer-valued parameters, use a difference = 1, and round the 46 regression results after each iteration

Copyright Murray Woodside 2010 Dealing with problems Tutorial for the WOSP/SIPEW Workshop, Jan 2010 ● Don’t Panic if a model seems to be nonsense § look at its predictions w there may be a trend, like underestimating delay at high loads, that indicates additional resource use (e. g. paging) § you may have to constrain the model more, or add more freedom to fit ● include a latency, it vacuums up simple things that have been left out ● some models have undetermined parameters. For instance a pair of parameters may have interchangeable effects on the measured variables § so that many combinations of values can be fitted, with 47 the same E. . . fix one, or simplify the structure

Copyright Murray Woodside 2010 Rank of H Tutorial for the WOSP/SIPEW Workshop, Jan 2010 ● the iteration may stop on a singular matrix M = St H(x, ut)TR-1 H(x, ut) ● examine the rank of M § it must be at least n § h must be sensitive to every parameter x, in some condition u. ● a high condition number of M may signal poor convergence behaviour ● you may have to introduce more variation in ut § more variation in the test conditions § this amounts to design of better tests, for predictive 48 purposes

Copyright Murray Woodside 2010 Open systems Tutorial for the WOSP/SIPEW Workshop, Jan 2010 ● For modeling purposes I personally prefer to model open systems as if closed § better behaved calculations, you never get infinite response times or infeasible processor demands § choose a very large N for the population § to get roughly a fixed throughput f/sec, calculate Z = N/f 49 ● if I want to extrapolate to higher throughputs I need a big enough N

Copyright Murray Woodside 2010 Where do curve-fit models come in? Tutorial for the WOSP/SIPEW Workshop, Jan 2010 ● e. g. , a polynomial curve fitted to each measure ● you can do this with the same techniques § hi (x, u) = polynomial in elements of u, with coefficients x to be found. § such a model can be compared by an F test ● the disadvantage of ad hoc functions for h is the lack of performance semantics § extrapolation is less robust 50

Copyright Murray Woodside 2010 Conclude Tutorial for the WOSP/SIPEW Workshop, Jan 2010 ● the tools exist to calibrate models from easily obtained data § avoid the most intrusive monitoring ● not too much data is required ● some issues not dealt with here § missing data (or, different measures taken in different trials) 51

Copyright Murray Woodside 2010 Some references 52 Tutorial for the WOSP/SIPEW Workshop, Jan 2010 ● Most of these ideas are described in the SIPEW 2008 keynote M. Woodside, “Performance Data and Performance Models”, Proc First SPEC Int Performance Engineering Workshop, Darmstadt, June 30, 2008. ● The integrated vision M. Woodside, G. Franks, D. C. Petriu, "The Future of Software Performance Engineering", Proc Future of Software Engineering 2007, at ICSE 2007, eds L. Briand, and A. Wolf, May 2007, pp 171 -187. ● An example of the application, to a SIP system Xiuping Wu, Murray Woodside, “ A Calibration Framework for Capturing and Calibrating Software Performance Models”, Proc European Performance Engineering Workshop 2008. ● A good general reference on regression, including the Newton-Raphson method described here: M. H. Kutner, C. J. Nachtsheim, J. Neter, W. Li, Applied Linear Statistical Models, 5 th edition, Mc. Graw Hill, 2005 D. M. Bates, D. G. Watts, Nonlinear Regression Analysis and its Applications, Wiley, 1988. ● Queueing models of performance: D. A. Menasce, V. A. F. Almeida, and L. W. Dowdy, Capacity Planning and Performance Modeling. Prentice-Hall, 1994. ● An overview of layered queueing, with further references: G. Franks, T. Al-Omari, M. Woodside, O. Das, Salem Derisavi, "Enhanced Modeling and Solution of Layered Queueing Networks", IEEE Trans. on Software Eng. Aug. 2008

Copyright Murray Woodside 2010 Regression and Performance Parameter Estimation ● Start will be at 9. 00 53 Tutorial for the WOSP/SIPEW Workshop, Jan 2010