Regression Regression n Correlation and regression are closely

Regression

Regression n Correlation and regression are closely related in use and in math. Correlation summarizes the relations b/t 2 variables. Regression is used to predict values of one variable from values of the other (e. g. , SAT to predict GPA).

Basic Ideas (2) n n Sample value: Intercept – place where X=0 Slope – change in Y if X changes 1 unit. Rise over run. If error is removed, we have a predicted value for each person at X (the line): Suppose on average houses are worth about $75. 00 a square foot. Then the equation relating price to size would be Y’=0+75 X. The predicted price for a 2000 square foot house would be $150, 000.

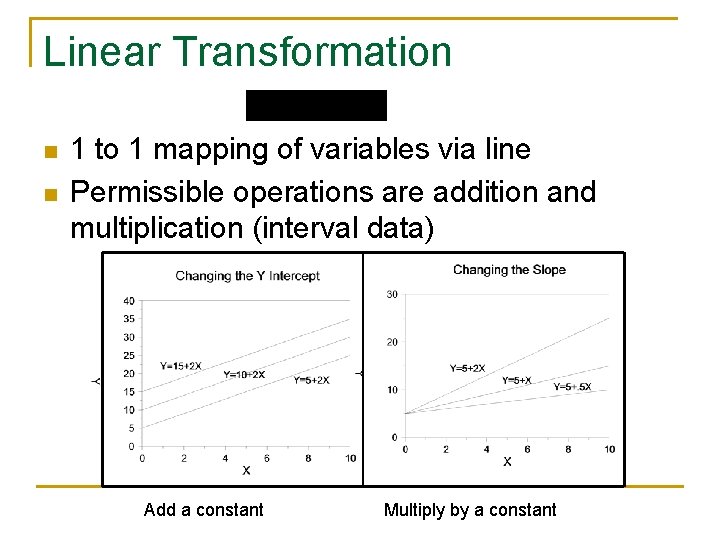
Linear Transformation n n 1 to 1 mapping of variables via line Permissible operations are addition and multiplication (interval data) Add a constant Multiply by a constant

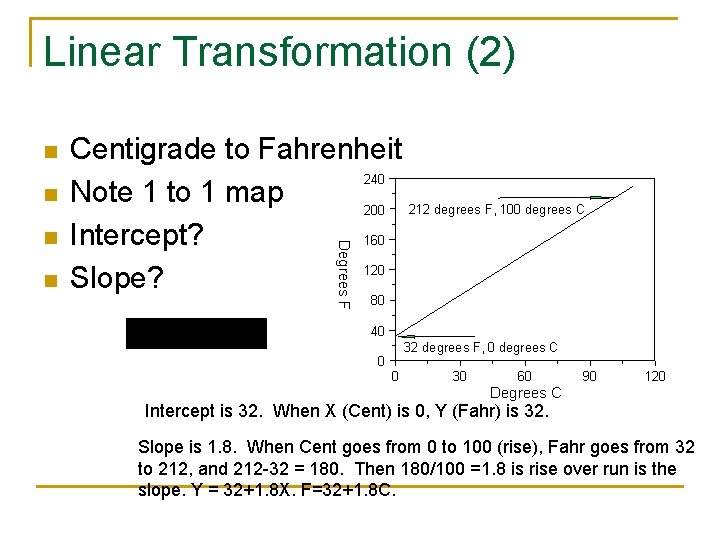
Linear Transformation (2) n n n Degrees F n Centigrade to Fahrenheit 240 Note 1 to 1 map 212 degrees F, 100 degrees C 200 160 Intercept? 120 Slope? 80 40 32 degrees F, 0 degrees C 0 0 30 60 90 120 Degrees C Intercept is 32. When X (Cent) is 0, Y (Fahr) is 32. Slope is 1. 8. When Cent goes from 0 to 100 (rise), Fahr goes from 32 to 212, and 212 -32 = 180. Then 180/100 =1. 8 is rise over run is the slope. Y = 32+1. 8 X. F=32+1. 8 C.

Regression Line (1) Basics 1. Passes thru both means. 2. Passes close to points. Note errors. 3. Described by an equation.

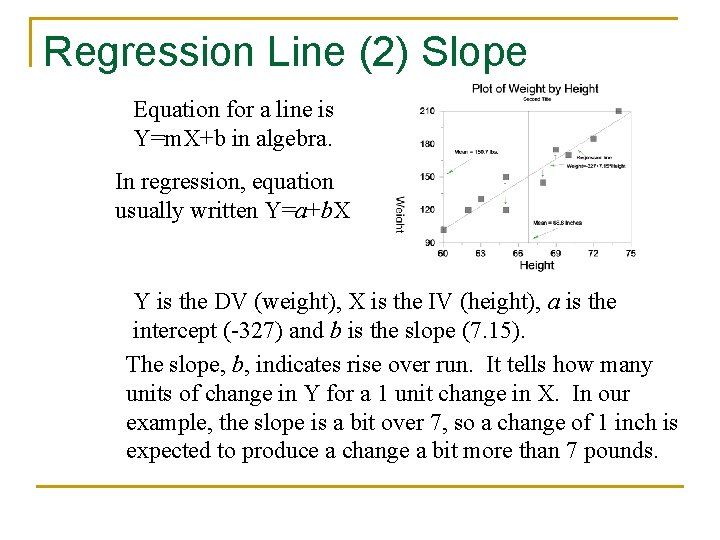
Regression Line (2) Slope Equation for a line is Y=m. X+b in algebra. In regression, equation usually written Y=a+b. X Y is the DV (weight), X is the IV (height), a is the intercept (-327) and b is the slope (7. 15). The slope, b, indicates rise over run. It tells how many units of change in Y for a 1 unit change in X. In our example, the slope is a bit over 7, so a change of 1 inch is expected to produce a change a bit more than 7 pounds.

Regression Line (3) Intercept The Y intercept, a, tells where the line crosses the Y axis; it’s the value of Y when X is zero. The intercept is calculated by: Sometimes the intercept has meaning; sometimes not. It depends on the meaning of X=0. In our example, the intercept is – 327. This means that if a person were 0 inches tall, we would expect them to weigh – 327 lbs. Nonsense. But if X were the number of smiles, then a would have meaning.

Correlation & Regression Correlation & regression are closely related. 1. The correlation coefficient is the slope of the regression line if X and Y are measured as z scores. Interpreted as SDY change with a change of 1 SDX. 2. For raw scores, the slope is: The slope for raw scores is the correlation times the ratio of 2 standard deviations. (These SDs are computed with (N-1), not N). In our example, the correlation was. 96, so the slope can be found by b =. 96*(33. 95/4. 54) =. 96*7. 45 = 7. 15. Recall that. Our intercept is 150. 77. 15*66. 8 -327.

Correlation & Regression (2) 3. The regression equation is used to make predictions. The formula to do so is just: Suppose someone is 68 inches tall. Predicted weight is -327+7. 15*68 = 159. 2.

Review n n What is the slope? What does it tell or mean? What is the intercept? What does it tell or mean? How are the slope of the regression line and the correlation coefficient related? What is the main use of the regression line?

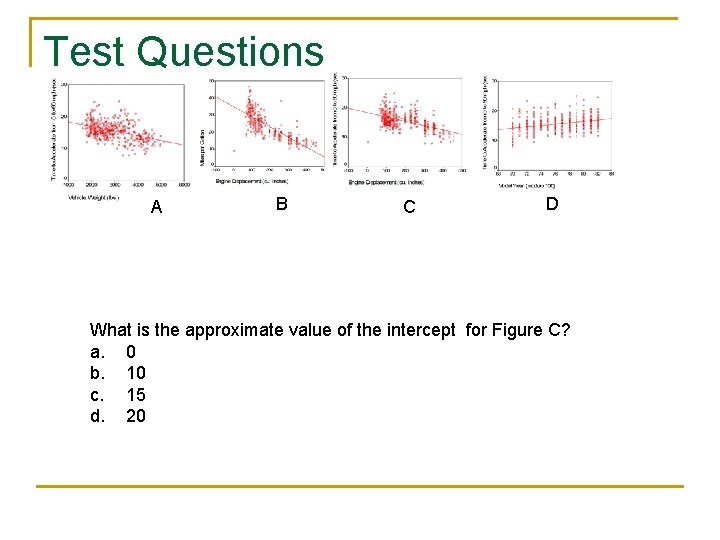
Test Questions A B C D What is the approximate value of the intercept for Figure C? a. 0 b. 10 c. 15 d. 20

Test Questions n n In a regression line, the equation used is typically. What does the value a stand for? q independent variable intercept predicted value (DV) q slope q q

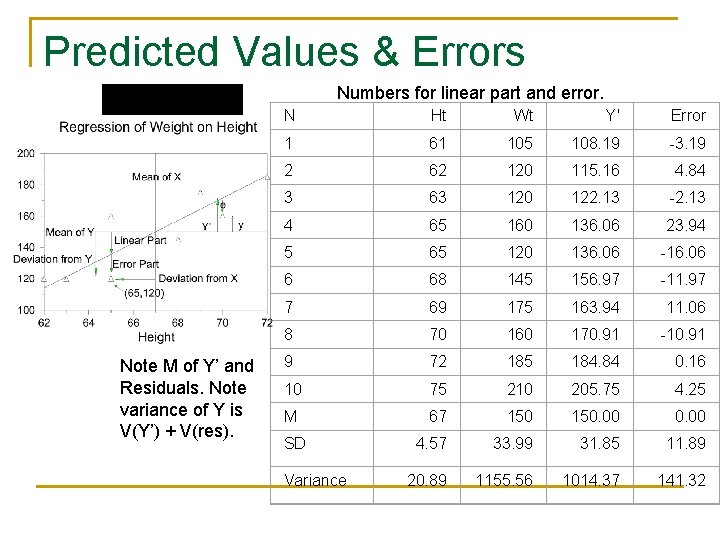
Regression of Weight on Height Ht Wt 61 105 62 120 63 120 65 160 65 120 68 145 69 175 70 160 72 185 75 210 N=10 M=67 M=150 Correlation (r) =. 94. SD=4. 57 SD= 33. 99 Regression equation: Y’=-361. 86+6. 97 X

Predicted Values & Errors Numbers for linear part and error. Note M of Y’ and Residuals. Note variance of Y is V(Y’) + V(res). N Ht Wt Y' Error 1 61 105 108. 19 -3. 19 2 62 120 115. 16 4. 84 3 63 120 122. 13 -2. 13 4 65 160 136. 06 23. 94 5 65 120 136. 06 -16. 06 6 68 145 156. 97 -11. 97 7 69 175 163. 94 11. 06 8 70 160 170. 91 -10. 91 9 72 185 184. 84 0. 16 10 75 210 205. 75 4. 25 M 67 150. 00 4. 57 33. 99 31. 85 11. 89 20. 89 1155. 56 1014. 37 141. 32 SD Variance

Error variance In our example, (Heiman’s notation for error is not standard. ) Standard error of the Estimate – average distance from prediction In our example

Variance Accounted for (Heiman’s notation for error is not standard. ) The basic idea is to try maximize r-square, the variance accounted for. The closer this value is to 1. 0, the more accurate the predictions will be.

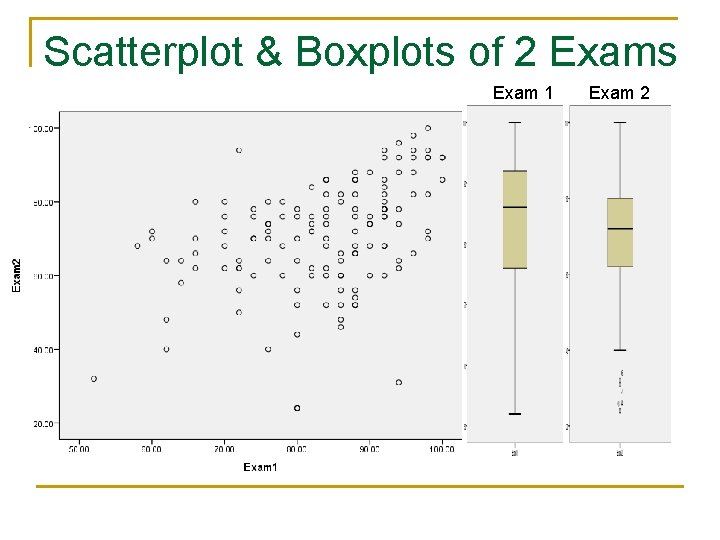
Sample Exam Data from Previous Class Exam 1 Exam 2 86. 00 98. 00 70. 00 84. 00 82. 00 92. 00 72. 00 96. 00 82. 00 56. 00 70. 00 76. 00 82. 00 74. 00 94. 00 78. 00 56. 00 66. 00 72. 00 A sample of 10 scores from both exams Assuming these are representative, what can you say about the exams? The students?

Scatterplot & Boxplots of 2 Exams Exam 1 Exam 2

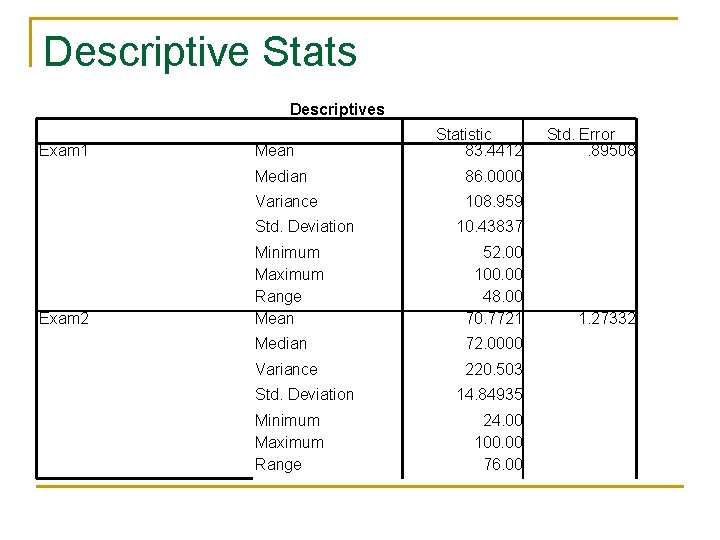
Descriptive Stats Descriptives Exam 1 Mean Median 86. 0000 Variance 108. 959 Std. Deviation Exam 2 Statistic 83. 4412 10. 43837 Minimum Maximum Range Mean 52. 00 100. 00 48. 00 70. 7721 Median 72. 0000 Variance 220. 503 Std. Deviation Minimum Maximum Range Std. Error. 89508 14. 84935 24. 00 100. 00 76. 00 1. 27332

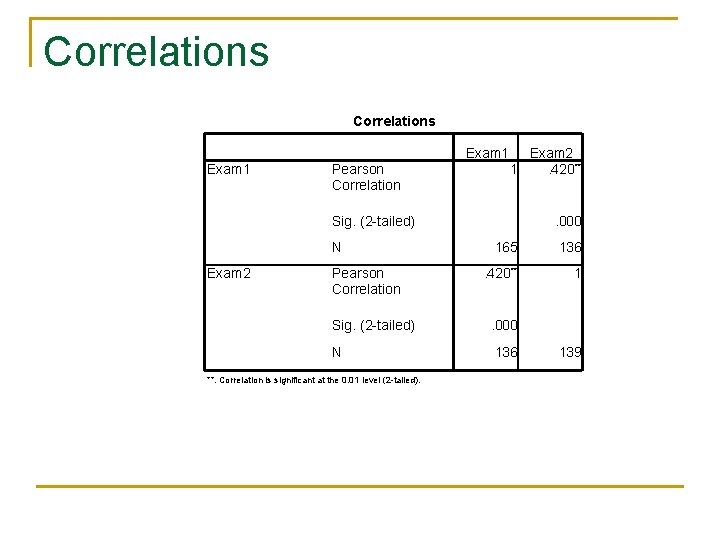
Correlations Exam 1 Pearson Correlation Exam 2 1. 420** Sig. (2 -tailed) N Exam 2 Pearson Correlation . 000 165 136 . 420** 1 Sig. (2 -tailed) . 000 N 136 **. Correlation is significant at the 0. 01 level (2 -tailed). 139

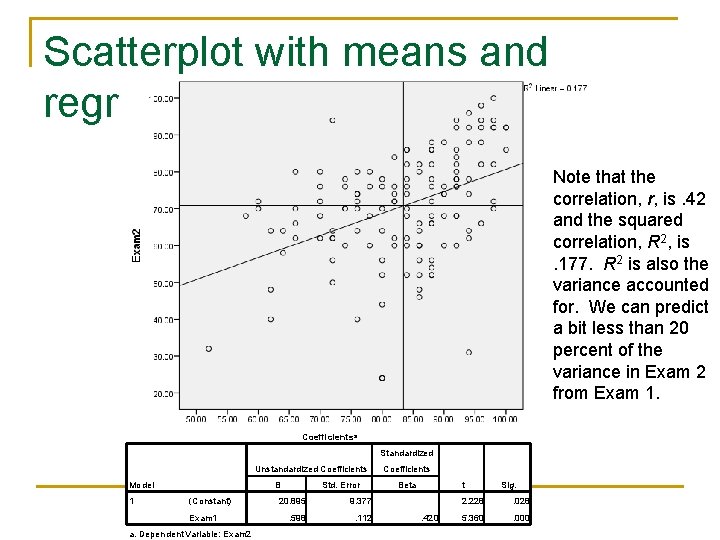
Scatterplot with means and regression line Note that the correlation, r, is. 42 and the squared correlation, R 2, is. 177. R 2 is also the variance accounted for. We can predict a bit less than 20 percent of the variance in Exam 2 from Exam 1. Coefficientsa Standardized Unstandardized Coefficients Model 1 B (Constant) Exam 1 a. Dependent Variable: Exam 2 Std. Error 20. 895 9. 377 . 598 . 112 Coefficients t Beta . 420 Sig. 2. 228 . 028 5. 360 . 000

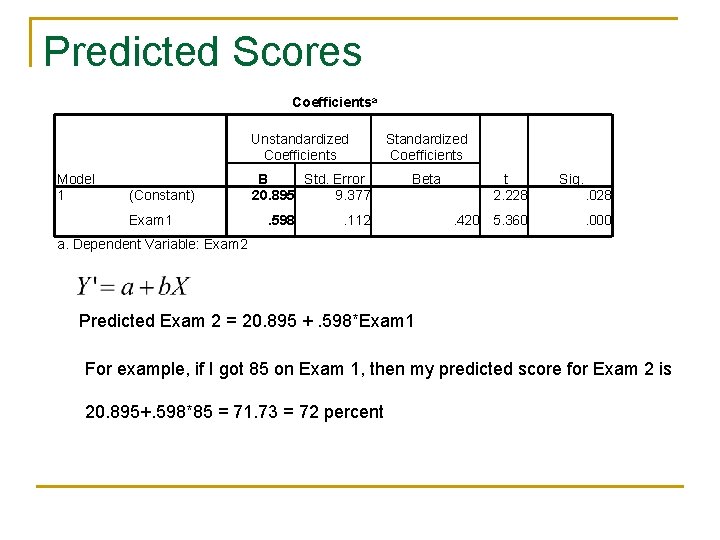
Predicted Scores Coefficientsa Unstandardized Coefficients Model 1 (Constant) Exam 1 B Std. Error 20. 895 9. 377. 598 Standardized Coefficients Beta . 112 t 2. 228. 420 5. 360 Sig. . 028. 000 a. Dependent Variable: Exam 2 Predicted Exam 2 = 20. 895 +. 598*Exam 1 For example, if I got 85 on Exam 1, then my predicted score for Exam 2 is 20. 895+. 598*85 = 71. 73 = 72 percent