Section 4 Parameter Estimation Fast Fracture ESTIMATION THEORY

Section 4: Parameter Estimation – Fast Fracture ESTIMATION THEORY - INTRODUCTION The parameters associated with a distribution must be estimated on the basis of a sample distributions obtained from a population. The role of sampling as it relates to the statistical inference and parameter estimation is outlined in the figure in the next overhead. The point is to construct a mathematical model that captures the population under study. This requires • inferring the type of distribution that best characterizes the population; and • estimating parameters once the distribution has been established. Thus sampling a population will yield information in order to establish values of the parameters associated with the chosen distribution.

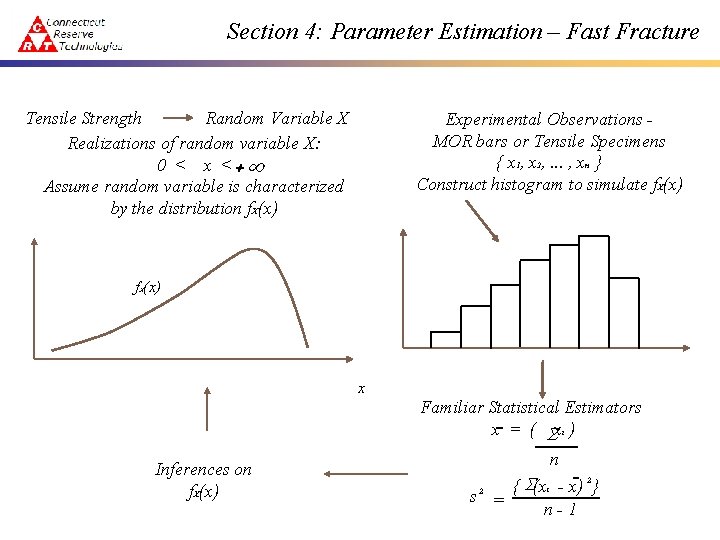
Section 4: Parameter Estimation – Fast Fracture Tensile Strength Random Variable X Realizations of random variable X: 0 < x < +¥ Assume random variable is characterized by the distribution f. X(x) Experimental Observations MOR bars or Tensile Specimens { x 1, x 2, . . . , xn } Construct histogram to simulate f. X(x) f (x) X x Familiar Statistical Estimators x = ( Sxi ) Inferences on f. X(x) n { S(xi - x) } s = n-1 2 2

Section 4: Parameter Estimation – Fast Fracture “Choosing” a distribution can be somewhat of a qualitative and subjective process. We stress that the physics that underlie a problem should indicate an appropriate choice. However, most times the engineer is left with somehow establishing a rational choice, and too often histograms and their shapes are relied on. However there are quantitative tools that can aid the engineer in his/her selection. These tools are known as goodness-of-fit tests, e. g, • Anderson-Darling Goodness-of-Fit Test Usually these types of tests will only indicate when the engineer chooses badly. For ceramics, the industry has focused on the two parameter Weibull distribution. This is a Type III minimum extreme value statistic. Thus physics and mathematics drives this selection. Once the type of distribution has been made, the next step involves parameter estimation. There are two types of parameter estimation • Point Estimates • Interval Estimates

Section 4: Parameter Estimation – Fast Fracture Point estimation is concerned with the calculation of a single number, from a sample of observations, that “best” represents the parameters associated with a chosen distribution. Interval estimation goes further and establishes a statement on the confidence in the estimated quantity. The result is the determination of an interval indicating the range wherein the true population parameter is located. This range is associated with a level of confidence. For a given number of samples the level of confidence increases with an increasing interval range. Alternatively, increasing the sample size will tend to decrease the interval range for a given level of confidence. Best possible combination is a large confidence and small interval size. The endpoints of the range define the “confidence bounds. ”

Section 4: Parameter Estimation – Fast Fracture POINT ESTIMATION - PRELIMINARIES In general, the objective of parameter estimation is the derivation of functions, i. e. , estimators, that are dependent on failure data, and that yield in some sense optimum estimates of the underlying population parameters. Various performance criteria can be applied to ensure that optimized estimates are obtained consistently. Two important criteria are: • Estimate Bias • Estimate Invariance Bias is a measure of the deviation of the estimated parameter value from the expected value of the population parameter. The values of point estimates computed from a number of samples will vary from sample to sample. If enough samples are taken one can generate statistical distributions for the point estimates, as a function of sample size. If the mean of a distribution for a parameter estimate is equal to the expected value of the parameter, the associated estimator is said to be unbiased.

Section 4: Parameter Estimation – Fast Fracture If an estimator yields biased results, the value of an individual estimate can easily be corrected if the estimator is invariant. An estimator is invariant if the bias associated with estimated parameter value is not functionally dependent on the true distribution parameters that characterize the underlying population. An example of an estimator that is not invariant is the linear regression estimators for the three-parameter Weibull distribution. There are three typical methods utilized in obtaining point estimates of distribution functions: • Method of moments • Linear regression techniques • Likelihood techniques

Section 4: Parameter Estimation – Fast Fracture METHOD OF MOMENTS

Section 4: Parameter Estimation – Fast Fracture MINIMIZING RESIDUALS No matter how refined our physical measurement techniques become, we can never ascertain the “true value” of anything. Thus we take repeated measurements of a quantity (say the distance between two corners of a property) and each time a measurement is conducted the values vary. Thus we are confronted with the dilemma of what value best represents the quantity measured. Several options include • Mean • Median • Mode Faced with options, one should question which approach yields the “best possible” value. To answer this question a systematic approach is needed such that one can say “This is the best possible value since this quantity is minimized” or “This is the best possible answer since that quantity is maximized”

Section 4: Parameter Estimation – Fast Fracture Thus we begin by focusing on the distance measuring example cited earlier and identify If many observations are made of this distance, then it is quite possible that none of the observations within a sample will coincide with the “best possible” value. If we define the difference where

Section 4: Parameter Estimation – Fast Fracture A systematic approach that yields the “best possible” value surely must minimize the residual associated with each observation (unless the observation is aberrant for some reason, i. e. , the observation is an outlier). If we identify Then if this quantity is minimized, the resulting “best possible” value ( ) would have a quantifiable “goodness” associated with it, i. e. , that the sum of the residuals has been minimized.

Section 4: Parameter Estimation – Fast Fracture To minimize the sum of the residuals, take the derivative of the expression above with respect to , set the derivative equal to zero and solve for Setting this last expression equal to zero definitely minimizes the residuals, for if no measurements are taken, all the residuals are zero. There is obviously a logic fault here.

Section 4: Parameter Estimation – Fast Fracture If minimizing the sum of the residuals is initially appealing (but the results do not help) then minimizing the sum of the squares of the residuals should be no less appealing. Here then Thus if we wish to minimize the sum of the squares of the residuals, then the sample mean should be utilized as the “best possible” value.

Section 4: Parameter Estimation – Fast Fracture Note that we developed this argument in terms of deriving a best possible value for a series of measurements. This concept can be easily extended to estimating values for distribution parameters, where instead of making a “measurement, ” we take a sample from the underlying population. Minimizing the sum of the squares of the residuals is not the only systematic approach in producing the “best possible” estimates of distribution parameters. The maximum likelihood technique is another systematic approach where a “likelihood” is maximized. In some instances the estimators from various methods coincide, most times they do not. In situations where different approaches produce different estimators (and estimates), then one must choose between the different techniques. The amount of bias produced by an estimator is one measure of assessing efficacy. There are other statistical tools available.

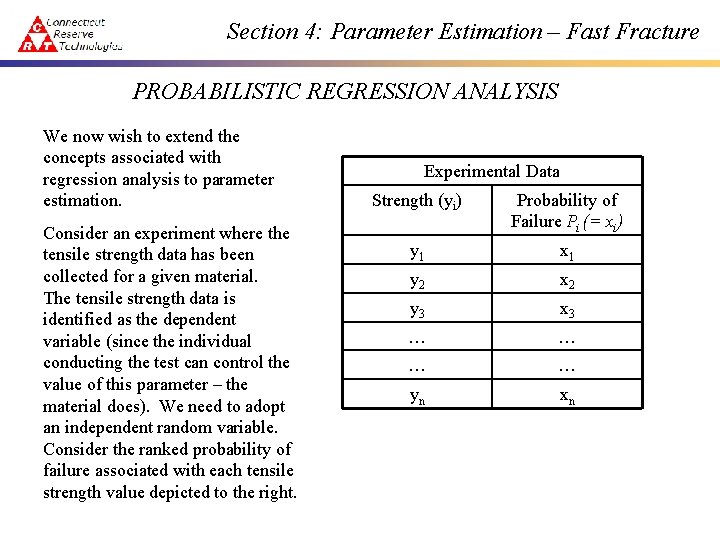
Section 4: Parameter Estimation – Fast Fracture PROBABILISTIC REGRESSION ANALYSIS We now wish to extend the concepts associated with regression analysis to parameter estimation. Consider an experiment where the tensile strength data has been collected for a given material. The tensile strength data is identified as the dependent variable (since the individual conducting the test can control the value of this parameter – the material does). We need to adopt an independent random variable. Consider the ranked probability of failure associated with each tensile strength value depicted to the right. Experimental Data Strength (yi) Probability of Failure Pi (= xi) y 1 x 1 y 2 x 2 y 3 x 3 … … yn xn

Section 4: Parameter Estimation – Fast Fracture Here yi = ith ranked tensile strength xi = P i = Associated ranked probability of failure The data is ranked in the following fashion y 1 < y 2 < y 3 <. . . < yn Thus it seems reasonable to expect P 1 < P 2 < P 3 <. . . < Pn x 1 < x 2 < x 3 <. . . < xn Note carefully that the individual conducting the experiment controls the value of n. This is important.

Section 4: Parameter Estimation – Fast Fracture The ranked data is in ascending order. But what are the probability values associated with each ranked data value? Consider the following observations: • x 1 corresponds to the lowest probability of failure • xn corresponds to the highest probability of failure • Assuming n is an even integer

Section 4: Parameter Estimation – Fast Fracture To possibly account for these three observations, consider the following expression: For large n values, P 1 trends to zero and Pn approaches 1. If we adopt this expression it is quite clear that the individual conducting the experiment influences Pi (or xi) through the choice of n prior to testing. Thus Pi (or xi) should be considered the independent variable in the experiment. With data collected from the experiment the individual analyzing the data now assumes an underlying probability density function If this expression can be linearized we can apply linear regression techniques to find the parameters q 1 and q 2.

Section 4: Parameter Estimation – Fast Fracture LINEAR REGRESSION – TWO PARAMETER WEIBULL DISTRIBUTION If we assume that the probability of failure in our experiment is governed by a twoparameter Weibull distribution, i. e. where s is the applied load at failure, then this expression can be linearized as follows:

Section 4: Parameter Estimation – Fast Fracture If we take Then

Section 4: Parameter Estimation – Fast Fracture We can now make use of the traditional linear regression expressions for a and b Once a and b are determined the Weibull parameters m and sq can be extracted from the expressions on the previous page.

Section 4: Parameter Estimation – Fast Fracture PROBABILITY OF FAILURE – RANKING SCHEMES A number of ranking schemes for Pi have been proposed. A mean ranking scheme was introduced in the previous section. In this section a median ranking scheme is discussed. As Johnson (1951) points out, the usual method of statistical inference involves constructing a histogram, from which a smoothed probability density function is derived. However, small sample sizes present difficulties since histograms vary greatly with changes in class intervals. As an alternative to this, ordered statistics were developed whereby ranked failure data is utilized. Consider a sample with five observation, where the observations are arranged in an increasing numerical order. It would seem reasonable to assume that the first observation (lowest value) would represent a value where 20% of the entire population would fall below this value. Thus a Pi of 20% is assigned this ranked value. Similarly a value of 40%, 60%, 80% and 100% would be assigned to the other ranked observations.

Section 4: Parameter Estimation – Fast Fracture If we concentrate on the first observation, assuming that 20% of the entire population falls below this value is a fairly far-reaching assumption. Thus we will appeal to a statistical estimate of the population fraction that lies below this value. To illustrate the concept, consider a sample of five observations taken from a population whose probability density function and attending distribution parameters are known. This sample of five is repeated four times, and for each sample the data is arranged in ascending order. If the cumulative distribution function for the first value is computed, then F(x 1) = percentage of the population below the value of x 1

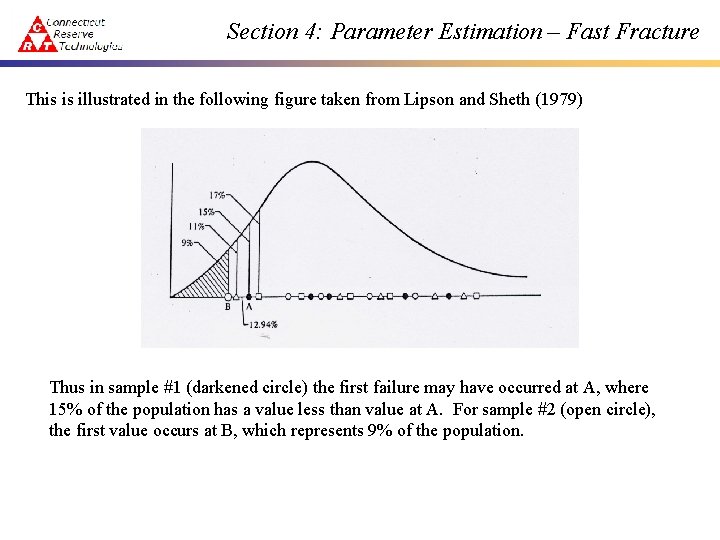
Section 4: Parameter Estimation – Fast Fracture This is illustrated in the following figure taken from Lipson and Sheth (1979) Thus in sample #1 (darkened circle) the first failure may have occurred at A, where 15% of the population has a value less than value at A. For sample #2 (open circle), the first value occurs at B, which represents 9% of the population.

Section 4: Parameter Estimation – Fast Fracture When this procedure is repeated many times the data generates a series of percentage values that are randomly distributed. The median value of this distribution is given by the expression Where n is the number of observations within a sample. Fro the second observation

Section 4: Parameter Estimation – Fast Fracture Thus in general Another ranking scheme proposed by Nelson (1982) had found wide acceptance. Here This estimator yields less bias then the median rank estimator, or the mean rank estimator. It is also the estimator accepted for use in ASTM 1239, and ISO Designation FDIS 20501.

Section 4: Parameter Estimation – Fast Fracture METHOD OF MAXIMUM LIKELIHOOD The method of maximum likelihood is the most commonly used estimation technique because the estimators derived by this approach maintain some very attractive features. Let (X 1, X 2, X 3, …, Xn) be a random sample of size n drawn from an arbitrary probability density function with one distribution parameter, i. e. , Here q is an unknown distribution parameter. The likelihood function of this random sample is defined as the joint density of the n random variables

Section 4: Parameter Estimation – Fast Fracture Often times it is much easier to manipulate the logarithm of the likelihood function, i. e. , The maximum likelihood estimator (MLE) of q identified as expression obtained by equating the derivative of to zero , is the root of the If there are more than one parameter associated with a distribution, then derivative of the log likelihood function is taken with respect to each unknown parameter, and each derivative is set equal to zero, i. e. ,

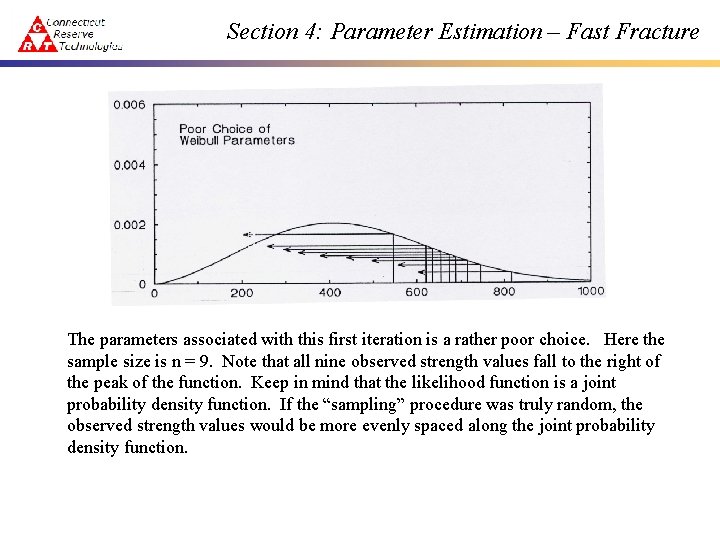
Section 4: Parameter Estimation – Fast Fracture where And k represents the number of parameters associated with a particular distribution. When more than one parameter must be estimated often times the system of equations obtained by taking the derivative of the log likelihood function must be solved in an iterative fashion, e. g. , as is done with the two parameter Weibull distribution inside the Weib. Par algorithm. The next two graphs illustrates how a first guess and then a subsequent iteration affects the likelihood function.

Section 4: Parameter Estimation – Fast Fracture The parameters associated with this first iteration is a rather poor choice. Here the sample size is n = 9. Note that all nine observed strength values fall to the right of the peak of the function. Keep in mind that the likelihood function is a joint probability density function. If the “sampling” procedure was truly random, the observed strength values would be more evenly spaced along the joint probability density function.

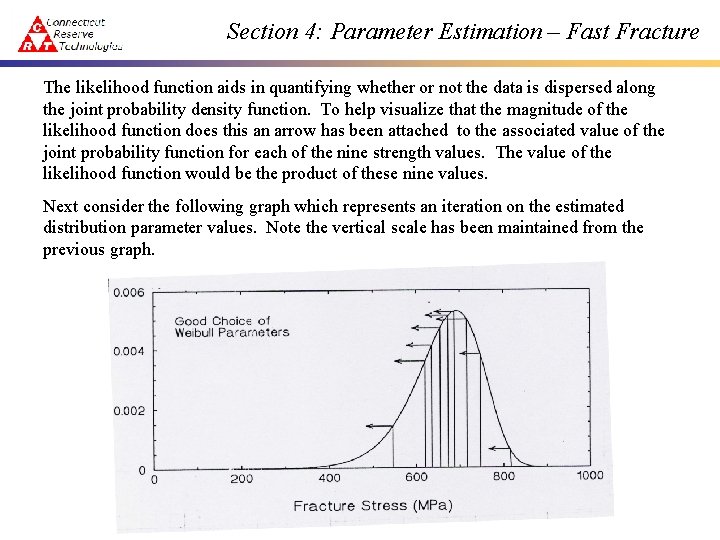
Section 4: Parameter Estimation – Fast Fracture The likelihood function aids in quantifying whether or not the data is dispersed along the joint probability density function. To help visualize that the magnitude of the likelihood function does this an arrow has been attached to the associated value of the joint probability function for each of the nine strength values. The value of the likelihood function would be the product of these nine values. Next consider the following graph which represents an iteration on the estimated distribution parameter values. Note the vertical scale has been maintained from the previous graph.

Section 4: Parameter Estimation – Fast Fracture The shape and position of the joint probability density function appear to be a much better fit to the nine data points. Again, we base judgment on the assumption that our data values represent a random sample and they should therefore span the range. Note for small sample sizes this assumption can easily break down. Again, nine arrows point to the associated values of the joint probability density function for each of the nine failure strengths. The product of these nine values represents the value of the likelihood function for this choice of distribution parameters. A simple inspection is sufficient to conclude that the likelihood from the latter iteration is greater than the likelihood from the former. If the latter choice of parameters is considered more acceptable, then this would indicate that obtaining a “best” set of distribution parameters involves maximizing the likelihood function. Two important properties of maximum likelihood estimators 1. Maximum likelihood estimators yield unique solutions 2. Estimates asymptotically converge to the true parameters as the sample size increases

Section 4: Parameter Estimation – Fast Fracture MLE – TWO PARAMETER WEIBULL DISTRIBUTION

Section 4: Parameter Estimation – Fast Fracture

Section 4: Parameter Estimation – Fast Fracture MULTIPLE FLAW DISTRIBUTIONS

Section 4: Parameter Estimation – Fast Fracture