Differentials Intro The device on the first slide

Intro • The device on the first slide is called a micrometer…. it is

• Errors in measurement, like a small error in the diameter of a

• To measure the precise change in a mathematical function, such as a

After this lesson, you should be able to: • Understand the concept of a

Δx xΔx (Δx)2 A Simple Example x Let S(x) be the area of a

Δx xΔx (Δx)2 A Simple Example For any function of g(Δx), if x xΔx

Try This Find the equation of the line tangent to (1, 1). at (1,

Analysis x 0. 9 1. 0 1. 1 f(x) y Complete the table (1,

Analysis x 0. 9 1. 0 1. 1 f(x). 81 1 y . 8

Linear Approximation to a Function Linear Approximation or TANGENT LINE!!!!!

Important Idea The equation of the line tangent to f(x) at c can be

In many types of application, the differential of y can be used as an

Animated Graphical View • Note how the "del y" and the dy in the

Example 1 Find dy for f (x) = x 2 + 3 x and

Derivatives in differential form Function derivative differential y=xn y ’ = n x n-1

Finding Differentials Function y = x 2 y = 2 sin x y =

Try This Find the differential dy of the function:

Find the tangent line approximation of at the point (0, 1).

Example 1 Find the approximate value of the cubic root Solution Let’s consider the

Example Practice Find the approximate value of square root Solution Let’s consider the function

Example 1 • Estimate ( 64. 3 ) Let y= (x) 1/3 64. 3

• = 4 + 1 / 160 = 4 By calculator, ( 64.

Error Propagation Physicists and engineers tend to make liberal use of the approximation of

Propagated Error • Consider a rectangular box with a square base 2 x –

Propagated Error • We know that • Then dy = 6 x 2 dx

Propagated Error • The propagated error is the dy – sometimes called the df

Example 2 The radius of a sphere is measured to be 6 inches, with

Calculating Differentials The differentiation rules we learned in Chapter 2 can be migrate to

Calculating Differentials Don’t forget the chain rule in calculating the derivatives. The same rule

Example 3 Solution Find the differentials

Example 4 Solution Find the differentials

Example 5 Solution Find the differentials

Example 6 Find the differential dy in an implicit function if y is a

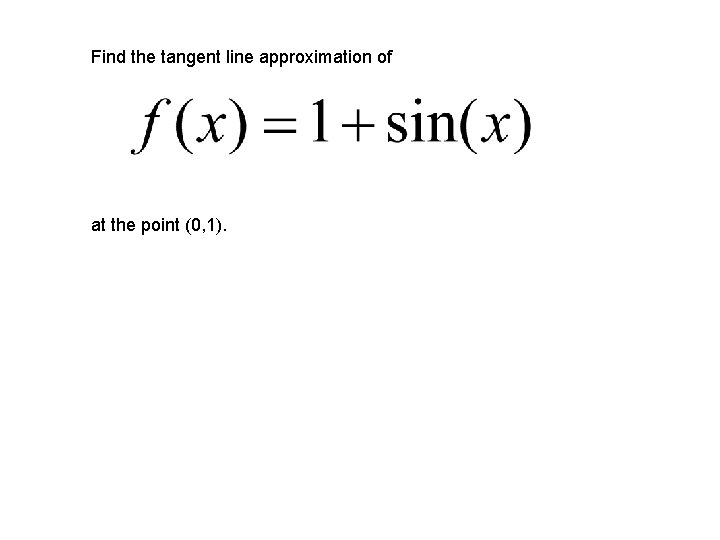
Slides: 61

Download presentation

Differentials

Intro • The device on the first slide is called a micrometer…. it is used for making precision measurements of the size of various objects…. . a small metal cube, the diameter of a ball bearing, etc…. • However, even a precision instrument like a micrometer has an error in measuring things….

• Errors in measurement, like a small error in the diameter of a ball bearing, can lead to major problems in an engine, if the ball bearing’s size is too far off from it’s allowed variation.

• To measure the precise change in a mathematical function, such as a change in an equation, we use Δy, the change in y. • But this can be messy to calculate ……. it would be nice to use a simpler way to represent the change in y, and using Calculus, we can !!!

After this lesson, you should be able to: • Understand the concept of a tangent line approximation. • Compare the value of the differential, dy, with the actual change in y, Δy. • Estimate a propagated error using a differential. • Find the differential of a function using differentiation formulas.

Δx xΔx (Δx)2 A Simple Example x Let S(x) be the area of a square of side length x. Or, S(x) = x 2 x Now we give the side a change Δx , then the corresponding change of area will be ΔS = S(x + Δx) – S(x) = (x + Δx)2 – x 2 = 2 xΔx + (Δx)2 Compare with Δx , (Δx)2 is the infinite smaller change. Or, xΔx Differentials Δx

Δx xΔx (Δx)2 A Simple Example For any function of g(Δx), if x xΔx Differentials Δx x We call g(Δx) is higher order of infinitesimal of Δx, denoted as ε(Δx). In other words, the change of area can be approximated to the first part of ΔS = S(x + Δx) – S(x) = 2 xΔx + (Δx)2 = 2 xΔx + ε(Δx) The first part above is linear to Δx. We call the first part as “Linear Principal Part ”.

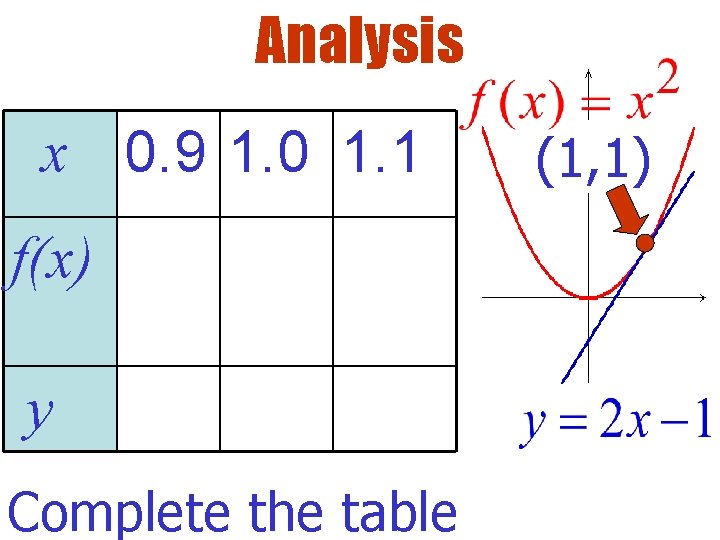
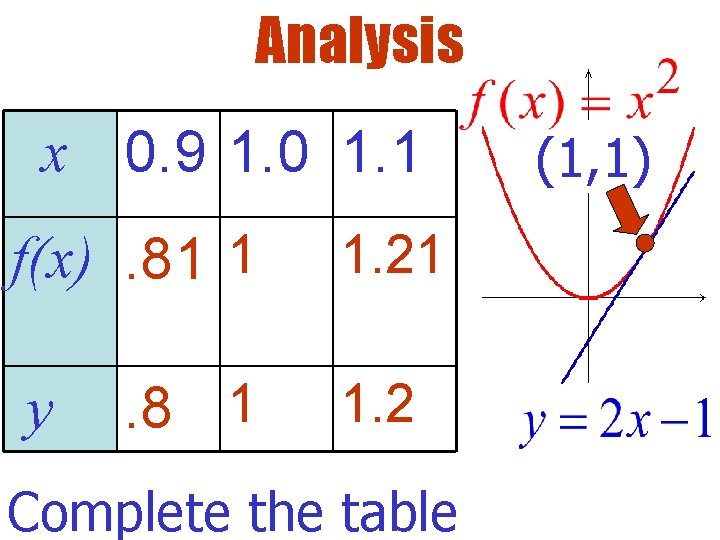
Try This Find the equation of the line tangent to (1, 1). at (1, 1)

Analysis x 0. 9 1. 0 1. 1 f(x) y Complete the table (1, 1)

Analysis x 0. 9 1. 0 1. 1 f(x). 81 1 y . 8 1 1. 2 Complete the table (1, 1)

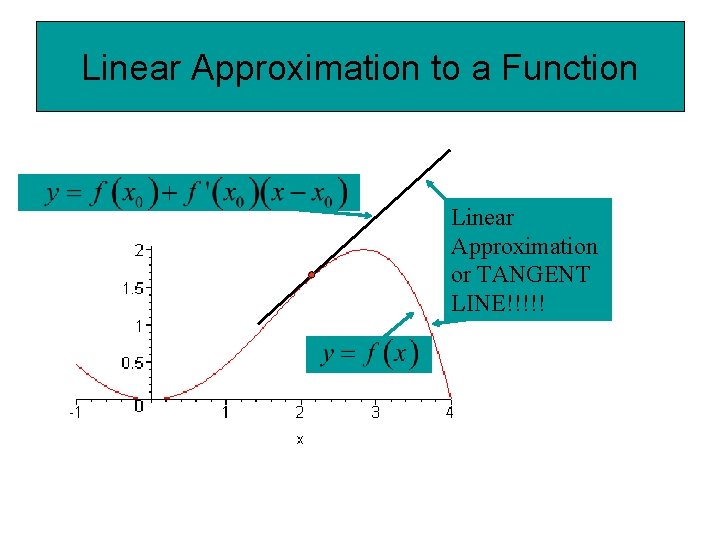
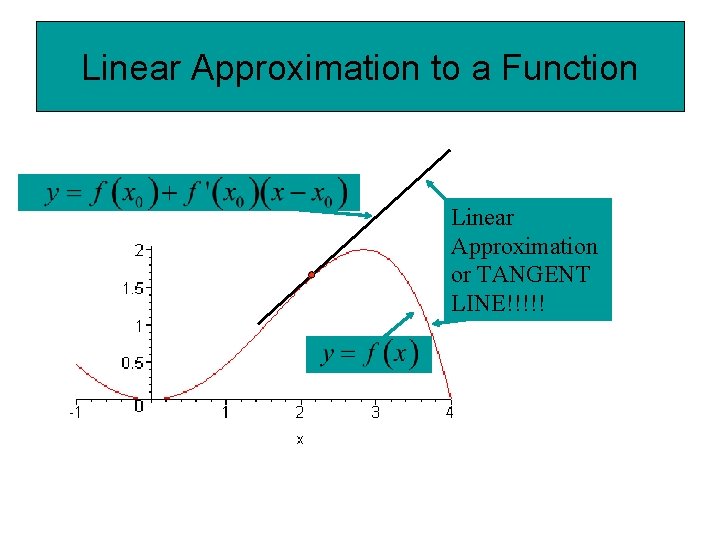
Linear Approximation to a Function Linear Approximation or TANGENT LINE!!!!!

Important Idea The equation of the line tangent to f(x) at c can be used to approximate values of f(x) near f(c).

Definition of Differentials

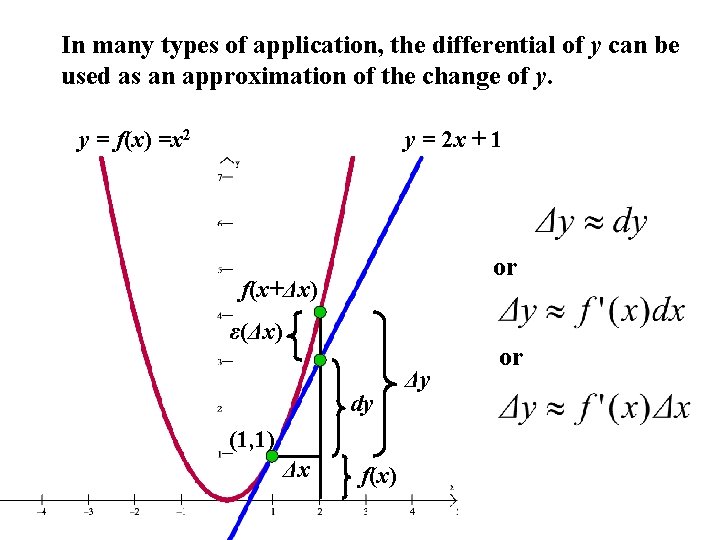
In many types of application, the differential of y can be used as an approximation of the change of y. y = f(x) =x 2 y = 2 x + 1 or f(x+Δx) ε(Δx) dy (1, 1) Δx f(x) Δy or

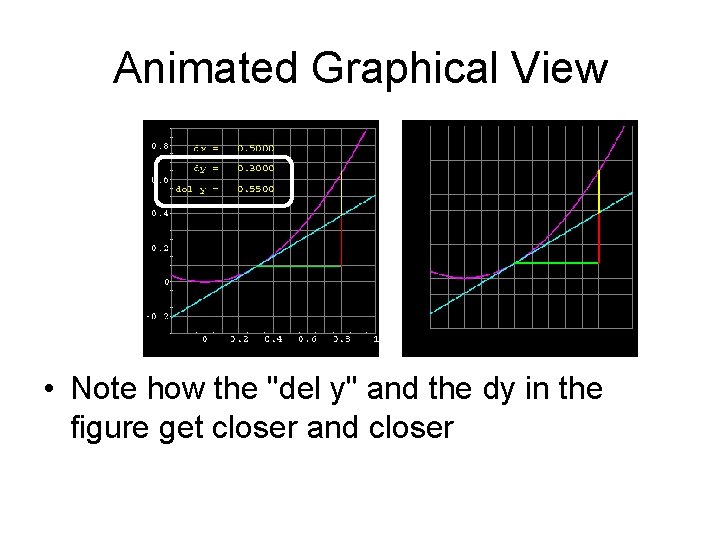
Animated Graphical View • Note how the "del y" and the dy in the figure get closer and closer

Example 1 Find dy for f (x) = x 2 + 3 x and evaluate dy for x = 2 and dx = 0. 1.

Example 1 Find dy for f (x) = x 2 + 3 x and evaluate dy for x = 2 and dx = 0. 1. Solution: dy = f ’(x) dx = (2 x + 3) dx When x = 2 and dx = 0. 1, dy = [2(2) + 3] 0. 1 = 0. 7.

Derivatives in differential form Function derivative differential y=xn y ’ = n x n-1 dy = n x n-1 dx y = UV y ′ = UV ′ + VU ′ dy = U d. V + V d. U y= U V y ’ = V U′ – U V′ V 2 dy = V d. U – U d. V V 2

Finding Differentials Function y = x 2 y = 2 sin x y = x cosx Derivative Differential

Try This Find the differential dy of the function:

Linear Approximation to a Function Linear Approximation or TANGENT LINE!!!!!

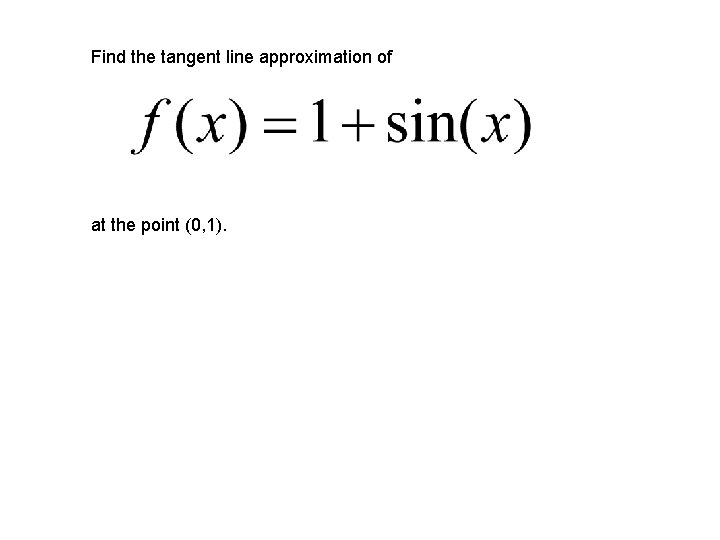
Find the tangent line approximation of at the point (0, 1).

Example 1 Find the approximate value of the cubic root Solution Let’s consider the function Δx = 0. 02, then and set x = 1,

Example Practice Find the approximate value of square root Solution Let’s consider the function Δx = – 0. 02, then and set x = 49,

Example 1 • Estimate ( 64. 3 ) Let y= (x) 1/3 64. 3 = 64 + 0. 3 Let x = 64 and Δx = 0. 3 = 3/10 So y + Δy ≈ y + dy and y + dy = ( 64 ) 1/3 dy = 1/3 x + 1/3 ( 64 ) -2/3 – 2/3 ( 3/10 ) = 4 + 1/3 ( 1/16 ) ( 3/ 10 ) dx

• = 4 + 1 / 160 = 4 By calculator, ( 64. 3 ) 1 = 4. 00625 160 1/3 = 4. 00624026 Not bad…. considering they had no calculator back then !!!

Error Propagation Physicists and engineers tend to make liberal use of the approximation of Δy by dy. One way this occrus in practice is in the estimation of errors propagated by physical measuring devices. x – measured value of a variable x + Δx – the exact value Δx – the error in measurement Measured Value Measurement Error If the measured value x is used to compute another value f(x), then Propagated Error f(x + Δx) – f(x) = Δy Exact Value

Propagated Error • Consider a rectangular box with a square base 2 x – Height is 2 times length of sides of base x x – Given that x = 3. 5 – You are able to measure with 3% accuracy • What is the error propagated for the volume?

Propagated Error • We know that • Then dy = 6 x 2 dx = 6 * 3. 52 * 0. 105 = 7. 7175 This is the approximate propagated error for the volume

Propagated Error • The propagated error is the dy – sometimes called the df • The relative error is • The percentage of error – relative error * 100%

Example 2 The radius of a sphere is measured to be 6 inches, with a possible error of 0. 02 inch. Use differentials to approximate the maximum possible error in calculating (a) The volume of the sphere (b) The surface area of the sphere (c) The relative errors in parts (a) and (b) Solution It is obvious that from the given information r = 6 inches and Δr = dr = ± 0. 02 inches (a) in 3

Calculating Differentials The differentiation rules we learned in Chapter 2 can be migrate to here Constant Multiple Sum or Difference Product Quotient

Calculating Differentials Don’t forget the chain rule in calculating the derivatives. The same rule is true in calculating the differentials

Example 3 Solution Find the differentials

Example 4 Solution Find the differentials

Example 5 Solution Find the differentials

Example 6 Find the differential dy in an implicit function if y is a function of x and Solution