ANALYSIS AND DESIGN OF ALGORITHMS UNITIII CHAPTER 6

ANALYSIS AND DESIGN OF ALGORITHMS UNIT-III CHAPTER 6: TRANSFORM-AND-CONQUER 1

OUTLINE Ø Presorting Ø Balanced Search Trees ü AVL Trees ü 2 -3 Trees Ø Heaps and Heapsort 2

Introduction Ø Transform-and-conquer technique o These methods work as two-stage procedures. (1) Transformation stage: the problem’s instance is modified to be, for one reason or another, more amenable to solution. (2) In the conquering stage, it is solved. 3

Transform and Conquer This group of techniques solves a problem by a transformation Ø to a simpler/more convenient instance of the same problem. We call it instance simplification. Ø to a different representation of the same instance. We call it representation change. Ø to a different problem for which an algorithm is already available. We call it problem reduction. Figure: Transform-and-conquer strategy. 4

Instance simplification - Presorting Solve a problem’s instance by transforming it into another simpler/easier instance of the same problem Presorting : Many problems involving lists are easier when list is sorted. Ø searching Ø checking if all elements are distinct (element uniqueness) Also: Ø Topological sorting helps solving some problems for dags. Ø Presorting is used in many geometric algorithms. 5

Element Uniqueness with presorting Ø Presorting-based algorithm Stage 1: sort by efficient sorting algorithm (e. g. merge sort). Stage 2: scan array to check pairs of adjacent elements. Efficiency: T(n) = Tsort(n) + Tscan(n) Є Θ(nlog n) + Θ(n) = Θ(nlog n) Ø Brute force algorithm Compare all pairs of elements Efficiency: Θ(n 2) 6

Example 1 Checking element uniqueness in an array. ALGORITHM Presort. Element. Uniqueness(A[0. . n - 1]) //Solves the element uniqueness problem by sorting the array first //Input: An array A[0. . n - 1] of orderable elements //Output: Returns “true” if A has no equal elements, “false” otherwise Sort the array A for i 0 to n - 2 do if A[i]= A[i + 1] return false return true Ø We can sort the array first and then check only its consecutive elements: if the array has equal elements, a pair of them must be next to each other and vice versa. 7

Example 2 Computing a mode Ø A mode is a value that occurs most often in a given list of numbers. For example, for 5, 1, 5, 7, 6, 5, 7, the mode is 5. Ø The brute-force approach for computing a mode would scan the list and compute the frequencies of all its distinct values, then find the value with the largest frequency. Ø To implement this, we can store the values already encountered, along with their frequencies, in a separate list. ü On each iteration, the ith element of the original list is compared with the values already encountered by traversing this auxiliary list. ü If a matching value is found, its frequency is incremented; otherwise, the current element is added to the list of distinct values with a frequency of 1. 8

Example 2 Computing a mode Ø Since list’s ith element is compared with i – 1 elements of the auxiliary list of distinct values seen so far before being added to the list with a frequency of 1, the worst-case number of comparisons made by this algorithm in creating the frequency list is n C(n) = ∑ (i-1) = 0 + 1 +. . . + (n-1) = (n-1)n Є Θ(n 2). 2 The additional n – 1 comparisons are needed to find the largest frequency in the auxiliary list. i=1 Ø In presort mode computation algorithm, the list is sorted first. Then all equal values will be adjacent to each other. To compute the mode, all we need to do is to find the longest run of adjacent equal values in the sorted array. Ø The efficiency of this presort algorithm will be nlogn, which is the time spent on sorting. 9

Example 2 Computing a mode ALGORITHM Presort. Mode(A[0. . n - 1]) //Computes the mode of an array by sorting it first //Input: An array A[0. . n - 1] of orderable elements //Output: The array’s mode Sort the array A i 0 //current run begins at position i modefrequency ← 0 //highest frequency seen so far while i ≤ n – 1 do runlength ← 1; runvalue ← A[i] while i + runlength ≤ n – 1 and A[i + runlength] = runvalue runlength ← runlength + 1 if runlength > modefrequency ← runlength; modevalue ← runvalue i ← i + runlength return modevalue 10

Example 3: Searching Problem: Search for a given K in A[0. . n-1] Presorting-based algorithm: Stage 1 Sort the array by an efficient sorting algorithm. Stage 2 Apply binary search. Efficiency: T(n) = Tsort(n) + Tsearch(n) = Θ(nlog n) + Θ(log n) = Θ(nlog n) 11

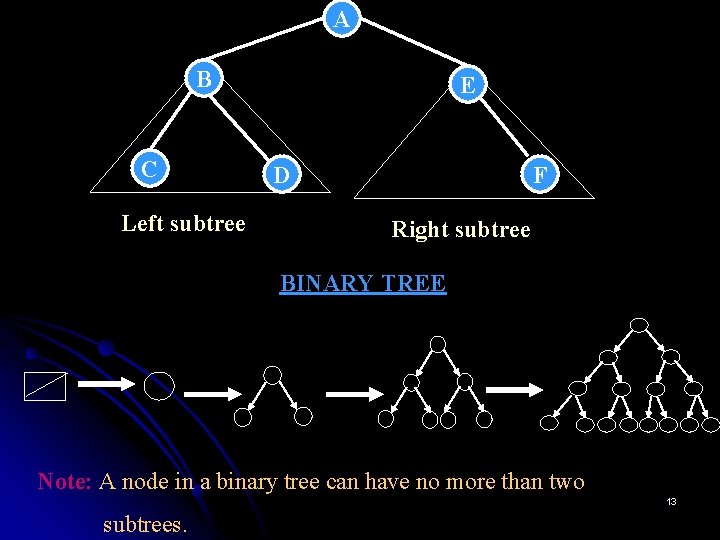
Binary Trees Ø Ø Binary Tree: A binary tree is a finite set of elements that is either empty or is partitioned into three disjoint subsets: - The first subset contains a single element called the ROOT of the tree. - The other two subsets are themselves binary trees, called the LEFT and RIGHT subtrees of the original tree. NODE : Each element of a binary tree is called a node of the tree. 12

A B C Left subtree E D F Right subtree BINARY TREE Note: A node in a binary tree can have no more than two 13 subtrees.

BINARY SEARCH TREE Binary Search Tree (Binary Sorted Tree) : Ø Suppose T is a binary tree. Then T is called a binary search tree if each node of the tree has the following property : the value of each node is greater than every value in the left subtree of that node and is less than every value in the right subtree of N. Ø Let x be a node in a binary search tree. If y is a node in the left subtree of x, then info(y)<info(x). If y is a node in the right subtree of x , then info(x)<=info(y) x All<x All≥x 14

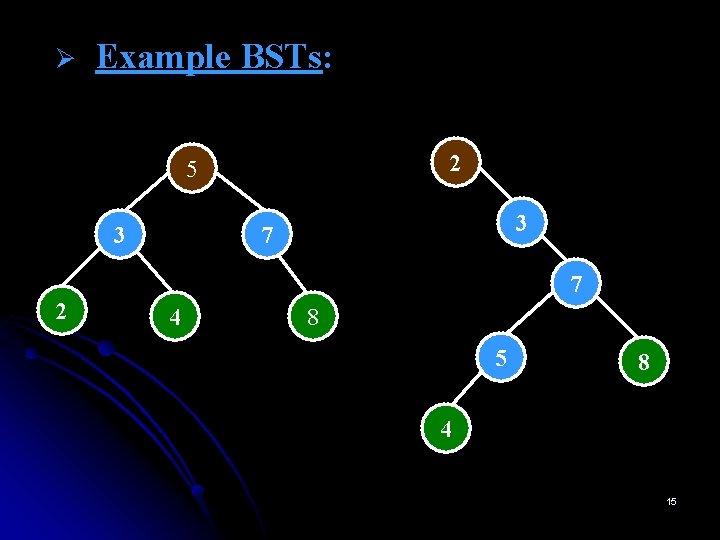
Ø Example BSTs: 2 5 3 3 7 7 2 4 8 5 8 4 15

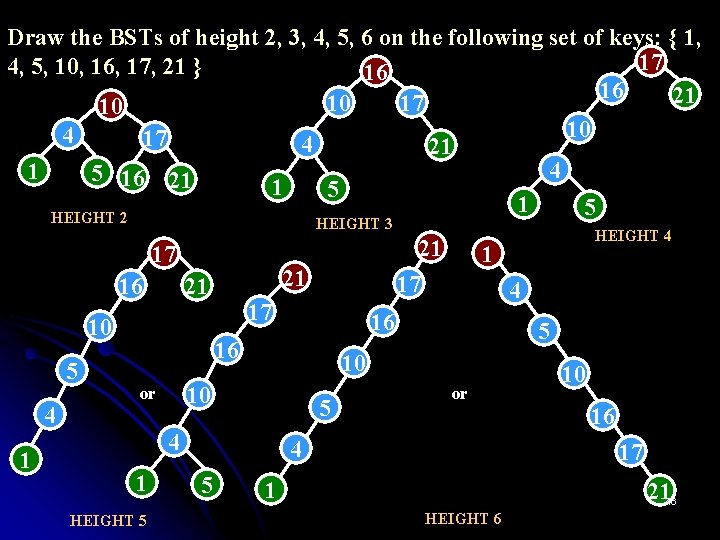
Draw the BSTs of height 2, 3, 4, 5, 6 on the following set of keys: { 1, 17 4, 5, 10, 16, 17, 21 } 16 16 21 10 17 10 10 4 17 4 21 4 1 5 16 21 1 5 HEIGHT 2 HEIGHT 3 17 16 5 4 1 21 21 10 21 17 17 5 4 1 HEIGHT 5 4 5 10 10 or 1 16 16 or 4 5 HEIGHT 4 10 16 17 1 2116 HEIGHT 6

Operations of BSTs: Insert n Adds an element x to the tree so that the binary search tree property continues to hold n The basic algorithm ¨ set the Index to Root ¨ Check if the data where index is pointing is NULL, if so Insert x in place of NULL, and finish the process. ¨ If the data is not NULL then compare the data with inserting item ¨ If the inserting item is equal or bigger then traverse to the right else traverse to the left. ¨ Continue with 2 nd step again until 17

Insert Operations: 1 st of 3 steps 1) The function begins at the root node and compares item 32 with the root value 25. Since 32 > 25, we traverse the right 2) subtree and look at node 35. 18

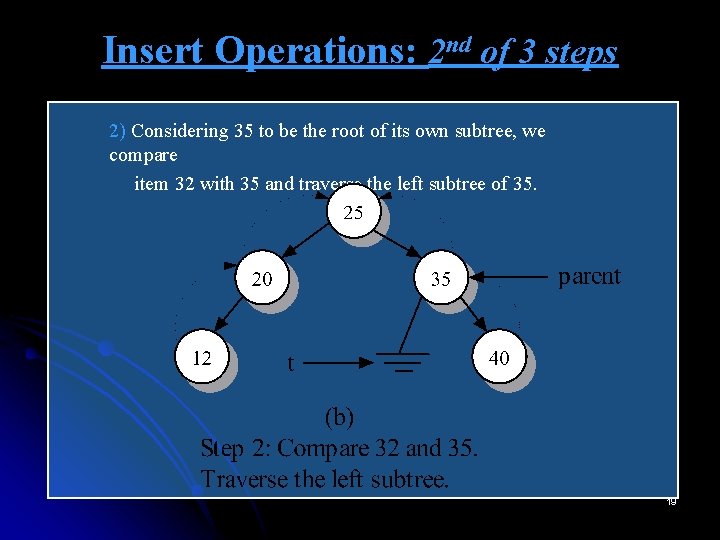
Insert Operations: 2 nd of 3 steps 2) Considering 35 to be the root of its own subtree, we compare item 32 with 35 and traverse the left subtree of 35. 19

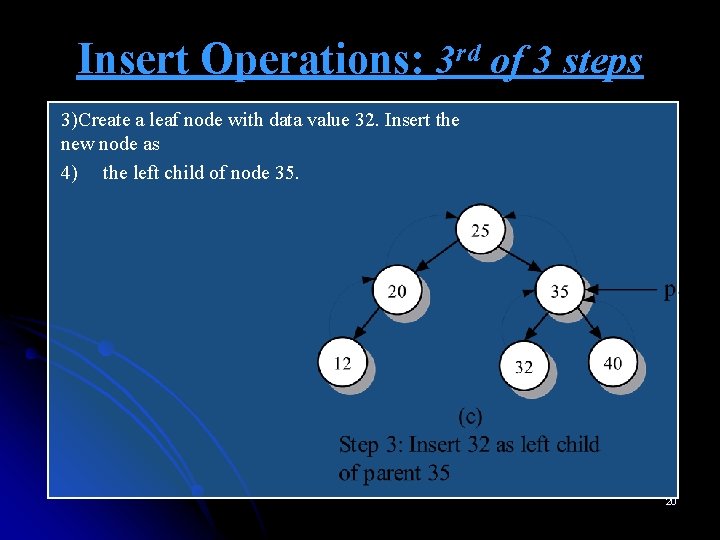
Insert Operations: 3 rd of 3 steps 3)Create a leaf node with data value 32. Insert the new node as 4) the left child of node 35. 20

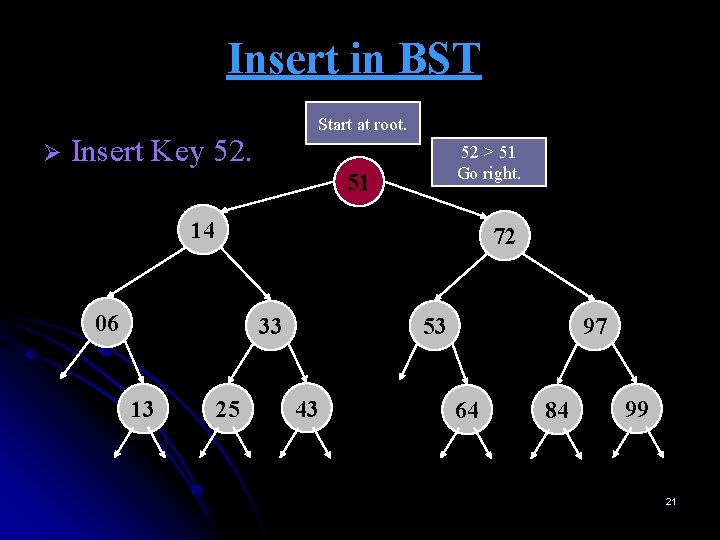
Insert in BST Ø Start at root. Insert Key 52. 52 > 51 Go right. 51 14 72 06 33 13 25 53 43 97 64 84 99 21

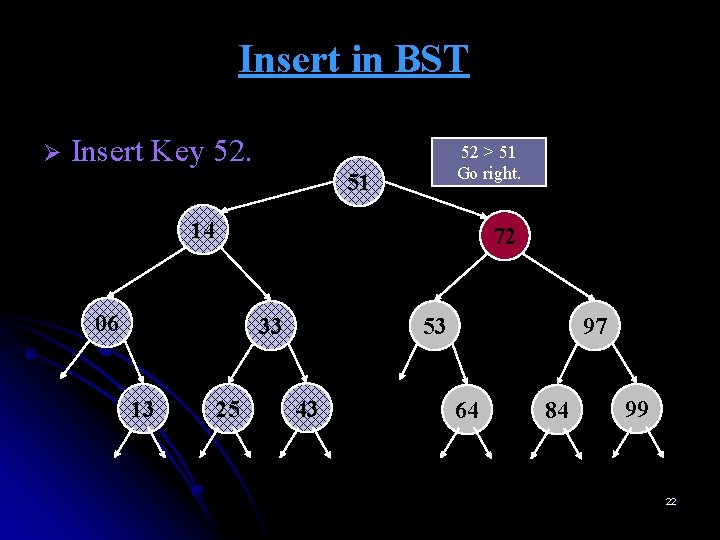
Insert in BST Ø Insert Key 52. 52 > 51 Go right. 51 14 72 06 33 13 25 53 43 97 64 84 99 22

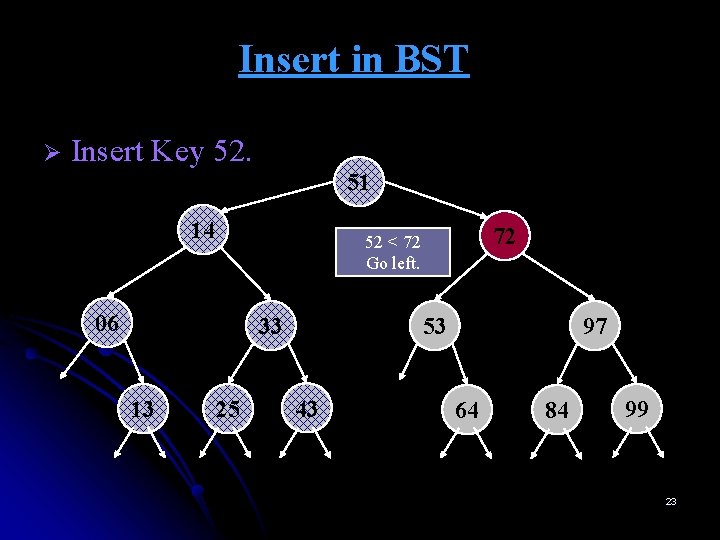
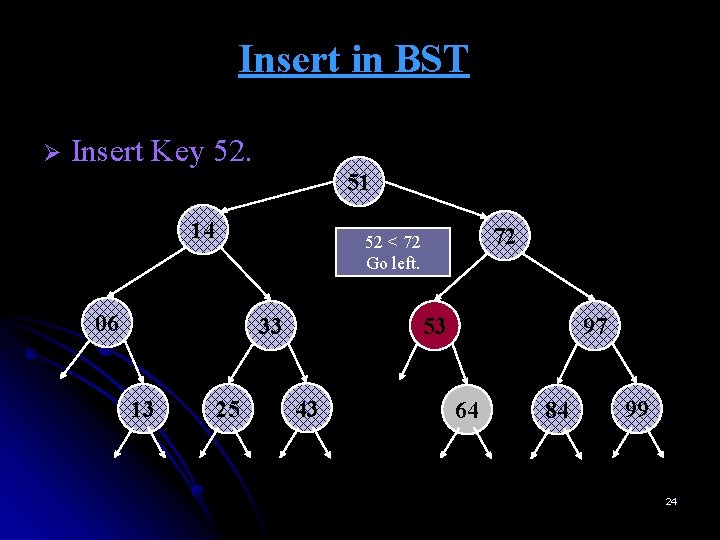
Insert in BST Ø Insert Key 52. 51 14 06 33 13 72 52 < 72 Go left. 25 53 43 97 64 84 99 23

Insert in BST Ø Insert Key 52. 51 14 06 33 13 72 52 < 72 Go left. 25 53 43 97 64 84 99 24

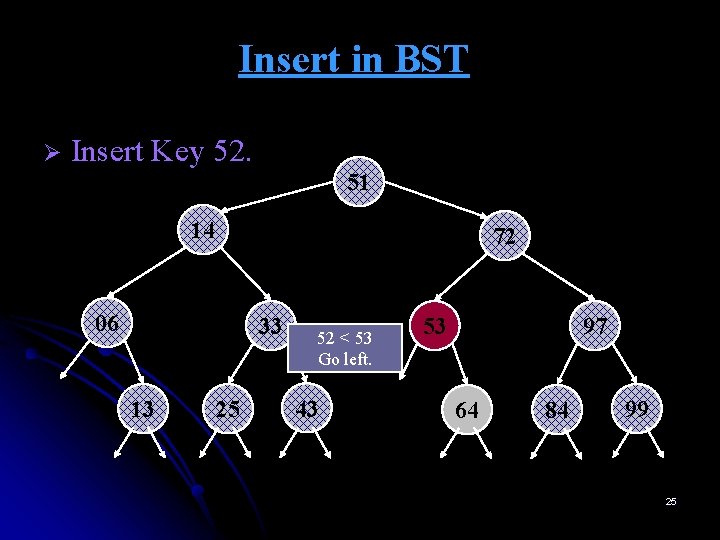
Insert in BST Ø Insert Key 52. 51 14 72 06 33 13 25 52 < 53 Go left. 43 53 97 64 84 99 25

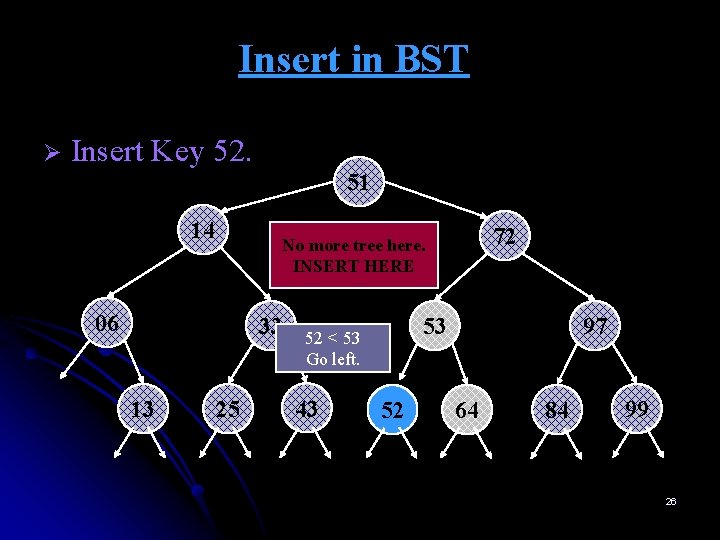
Insert in BST Ø Insert Key 52. 51 14 06 33 13 72 No more tree here. INSERT HERE 25 53 52 < 53 Go left. 43 52 97 64 84 99 26

Operations of BSTs: Search n looks for an element x within the tree n The basic algorithm ¨ Set the index to root ¨ Compare the searching item with the data at index ¨ If (the searching item is smaller) then traverse to the left else traverse to the right. ¨ Repeat the process until the index is point to NULL or found the item. 27

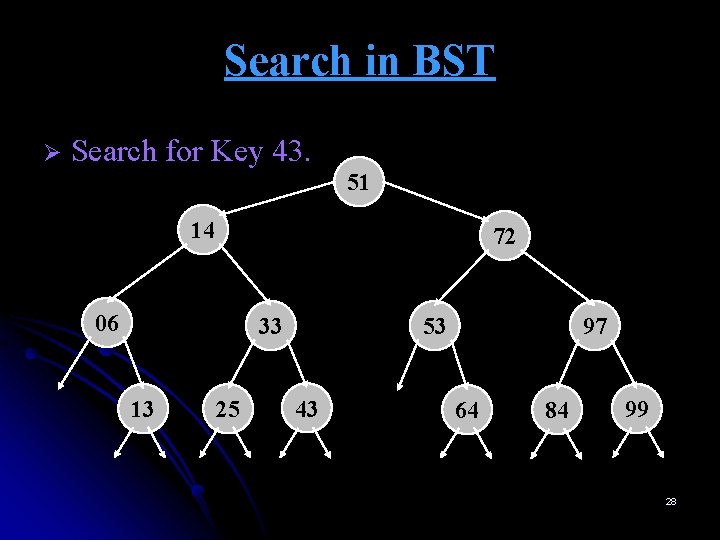
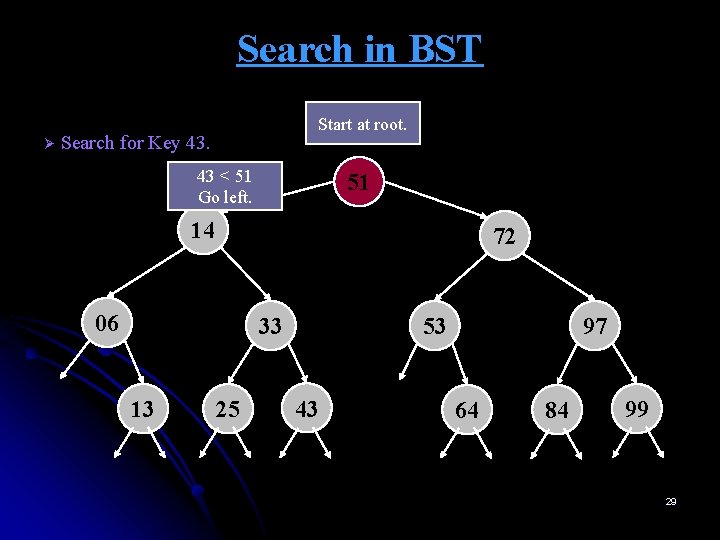
Search in BST Ø Search for Key 43. 51 14 72 06 33 13 25 53 43 97 64 84 99 28

Search in BST Ø Start at root. Search for Key 43. 43 < 51 Go left. 51 14 72 06 33 13 25 53 43 97 64 84 99 29

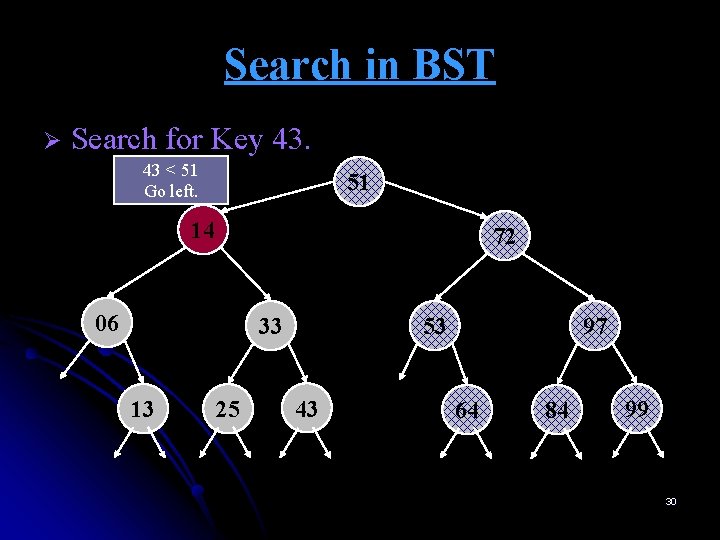
Search in BST Ø Search for Key 43. 43 < 51 Go left. 51 14 72 06 33 13 25 53 43 97 64 84 99 30

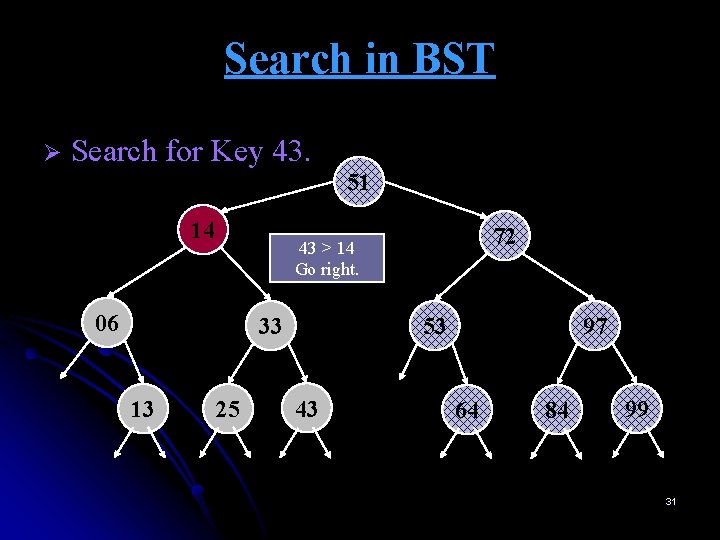
Search in BST Ø Search for Key 43. 51 14 06 33 13 72 43 > 14 Go right. 25 53 43 97 64 84 99 31

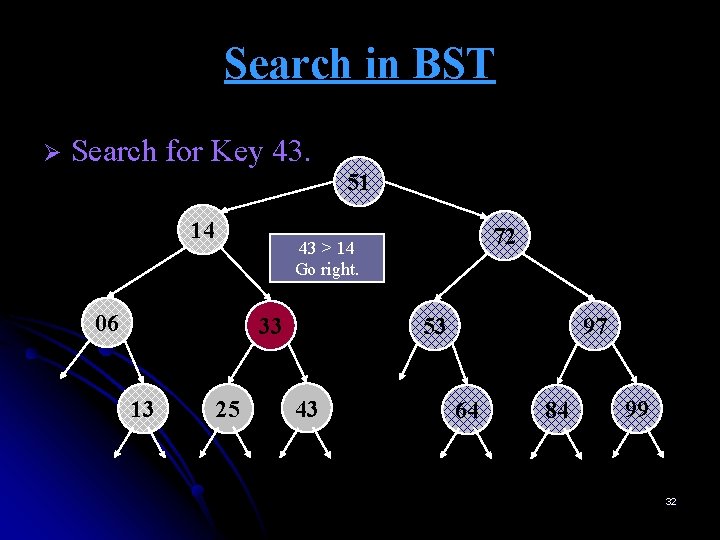
Search in BST Ø Search for Key 43. 51 14 06 33 13 72 43 > 14 Go right. 25 53 43 97 64 84 99 32

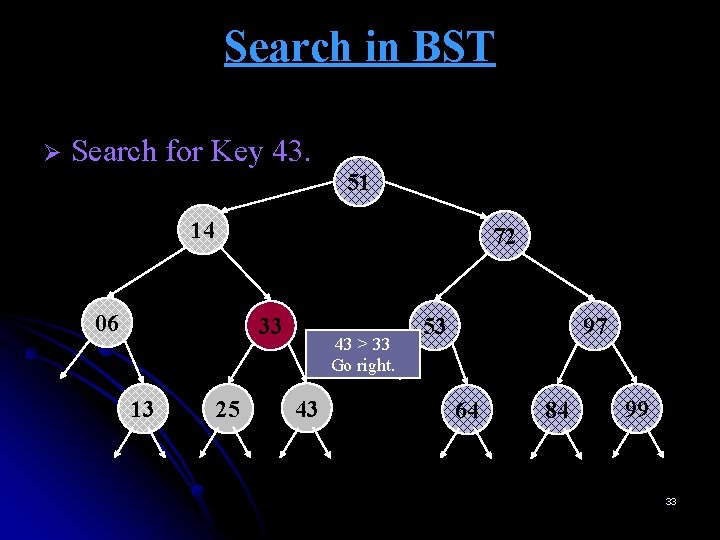
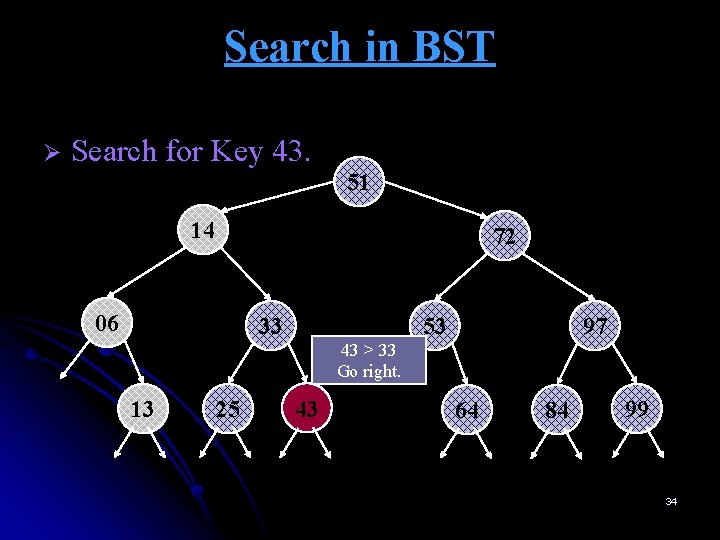
Search in BST Ø Search for Key 43. 51 14 72 06 33 13 25 43 > 33 Go right. 43 53 97 64 84 99 33

Search in BST Ø Search for Key 43. 51 14 72 06 33 53 97 43 > 33 Go right. 13 25 43 64 84 99 34

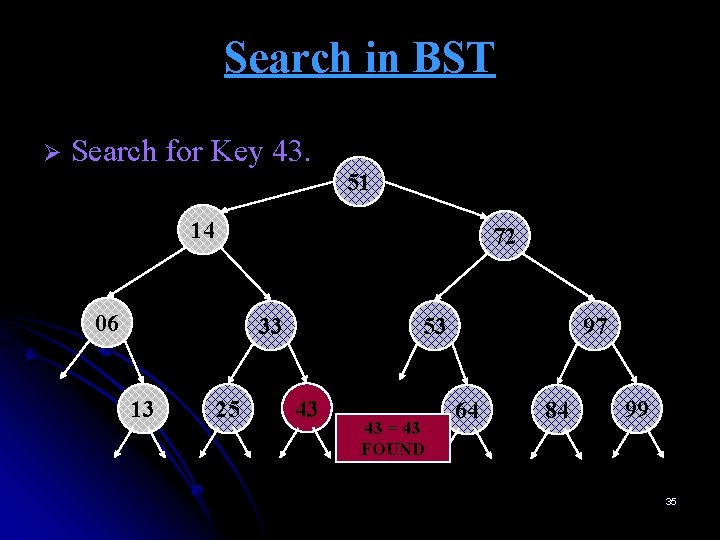
Search in BST Ø Search for Key 43. 51 14 72 06 33 13 25 53 43 43 = 43 FOUND 97 64 84 99 35

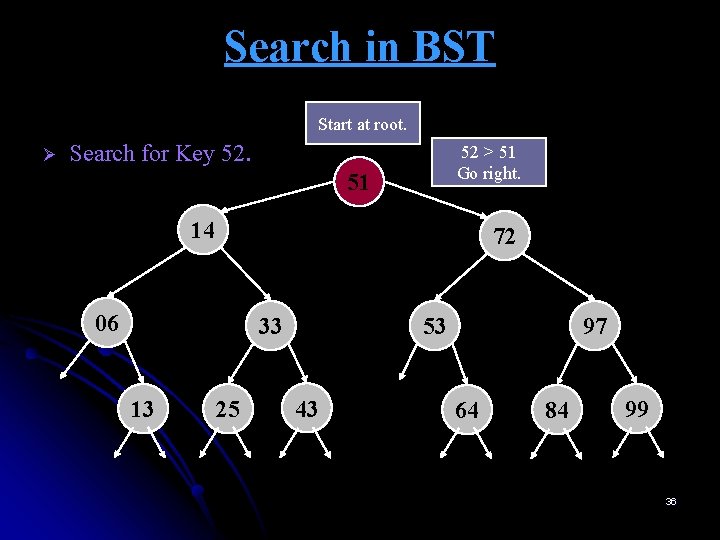
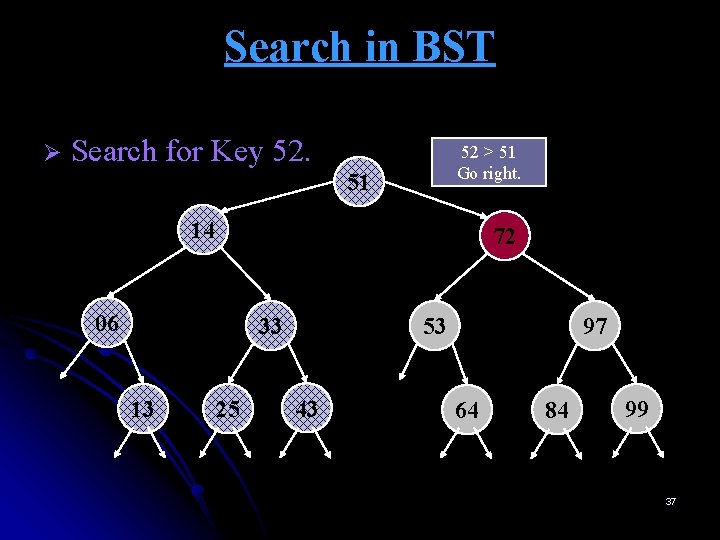
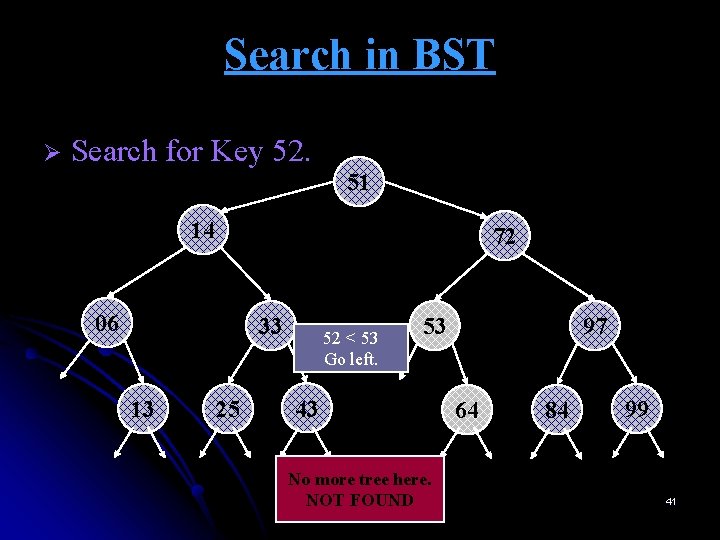
Search in BST Ø Start at root. Search for Key 52. 52 > 51 Go right. 51 14 72 06 33 13 25 53 43 97 64 84 99 36

Search in BST Ø Search for Key 52. 52 > 51 Go right. 51 14 72 06 33 13 25 53 43 97 64 84 99 37

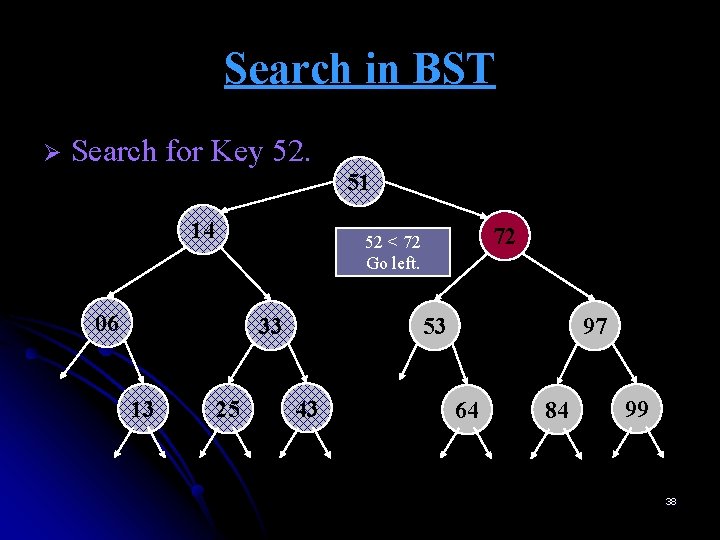
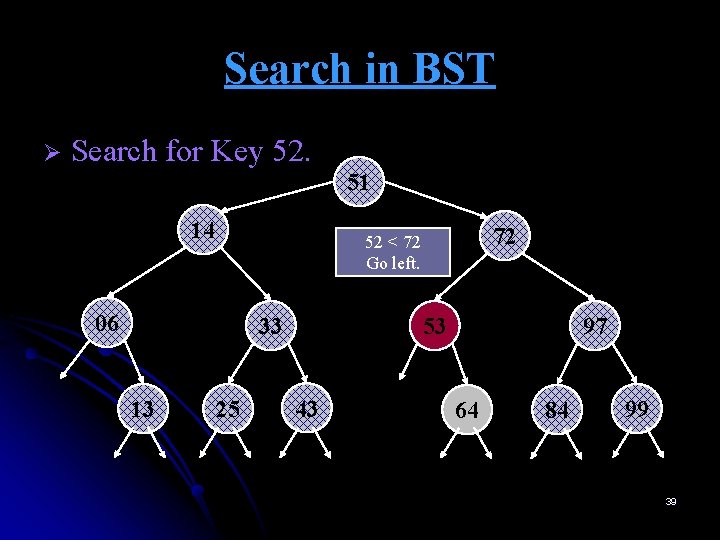
Search in BST Ø Search for Key 52. 51 14 06 33 13 72 52 < 72 Go left. 25 53 43 97 64 84 99 38

Search in BST Ø Search for Key 52. 51 14 06 33 13 72 52 < 72 Go left. 25 53 43 97 64 84 99 39

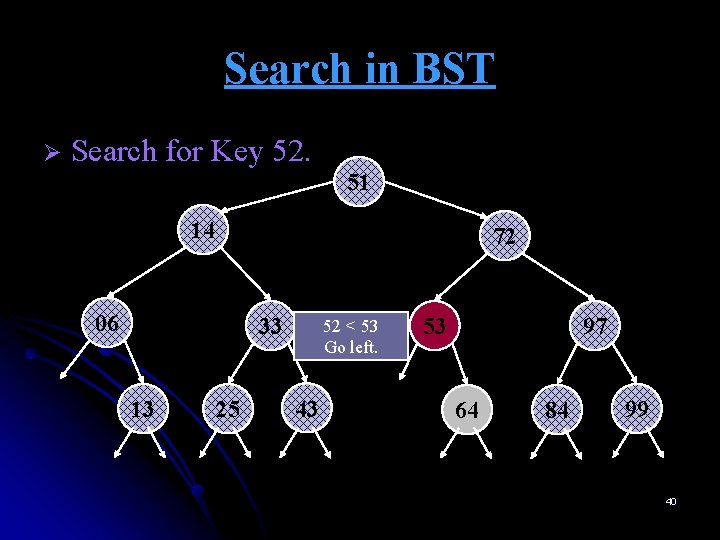
Search in BST Ø Search for Key 52. 51 14 72 06 33 13 25 52 < 53 Go left. 43 53 97 64 84 99 40

Search in BST Ø Search for Key 52. 51 14 72 06 33 13 25 52 < 53 Go left. 53 43 No more tree here. NOT FOUND 97 64 84 99 41

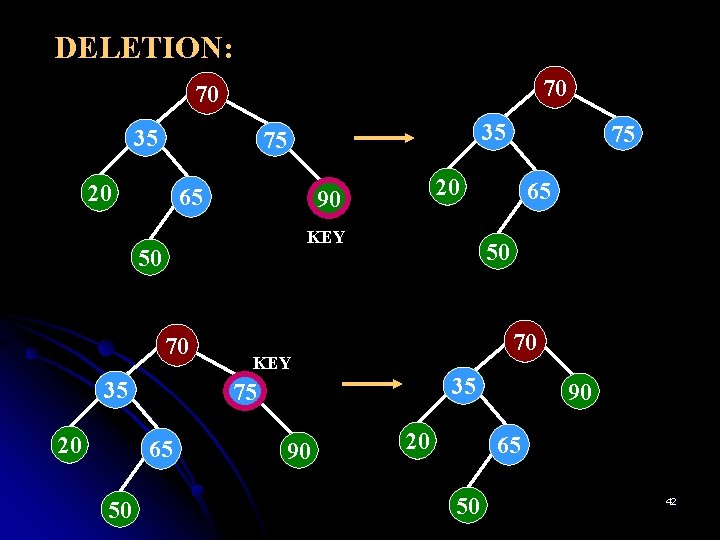
DELETION: 70 70 35 35 75 20 65 KEY 70 35 20 65 50 70 KEY 35 75 65 50 20 90 50 75 90 20 90 65 50 42

Binary Search Trees Ø The transformation from a set to a binary search tree is an example of the representation-change technique. Ø By doing this transformation, we gain in the time efficiency of searching, insertion, and deletion, which are all in Θ(log n), but only in the average case. In the worst case, these operations are in Θ(n). 43

Balanced Search Trees Ø There are two approaches to balance a search tree: v The first approach is of instance – simplification variety: an unbalanced binary search tree is transformed to a balanced one. An AVL tree requires the difference between the heights of the left and right subtrees of every node never exceed 1. Other types of trees are red-black trees and splay trees. v The second approach is of the representation-change variety: allow more than one element in a node of a search tree. Specific cases of such trees are 2 – 3 trees, 2 -3 -4 trees, B-trees. 44

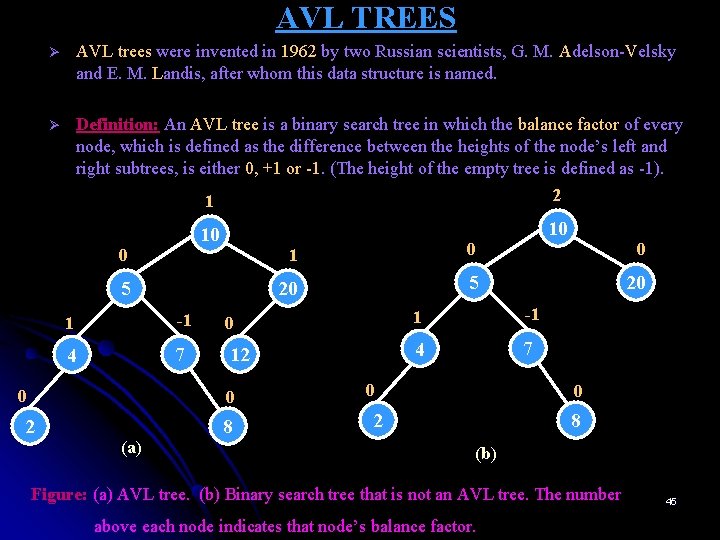
AVL TREES Ø AVL trees were invented in 1962 by two Russian scientists, G. M. Adelson-Velsky and E. M. Landis, after whom this data structure is named. Ø Definition: An AVL tree is a binary search tree in which the balance factor of every node, which is defined as the difference between the heights of the node’s left and right subtrees, is either 0, +1 or -1. (The height of the empty tree is defined as -1). 0 1 2 10 10 5 0 20 5 -1 0 1 -1 4 7 12 4 7 0 (a) 8 0 0 20 1 0 2 8 (b) Figure: (a) AVL tree. (b) Binary search tree that is not an AVL tree. The number above each node indicates that node’s balance factor. 45

AVL TREES Ø If an insertion of a new node makes an AVL tree unbalanced, we transform the tree by a rotation. Ø A rotation in an AVL tree is a local transformation of its subtree rooted at a node whose balance has become either +2 or -2; if there are several such nodes, we rotate the tree rooted at the unbalanced node that is the closest to the newly inserted leaf. Ø There are only four types of rotations: • Single right rotation (R-rotation) • Single left rotation (L-rotation) • Double left-right rotation (LR – rotation) • Double right-left rotation (RL – rotation) 46

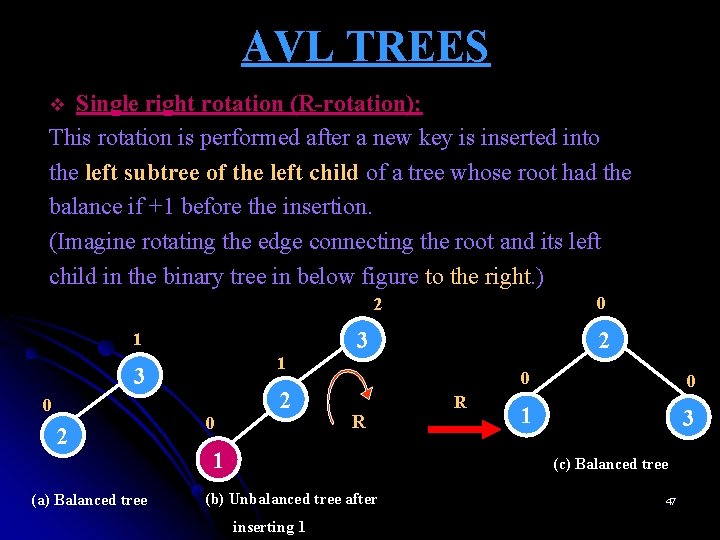
AVL TREES Single right rotation (R-rotation): This rotation is performed after a new key is inserted into the left subtree of the left child of a tree whose root had the balance if +1 before the insertion. (Imagine rotating the edge connecting the root and its left child in the binary tree in below figure to the right. ) v 0 2 1 1 3 0 2 (a) Balanced tree 0 2 2 3 R 1 R 0 0 1 3 (c) Balanced tree (b) Unbalanced tree after inserting 1 47

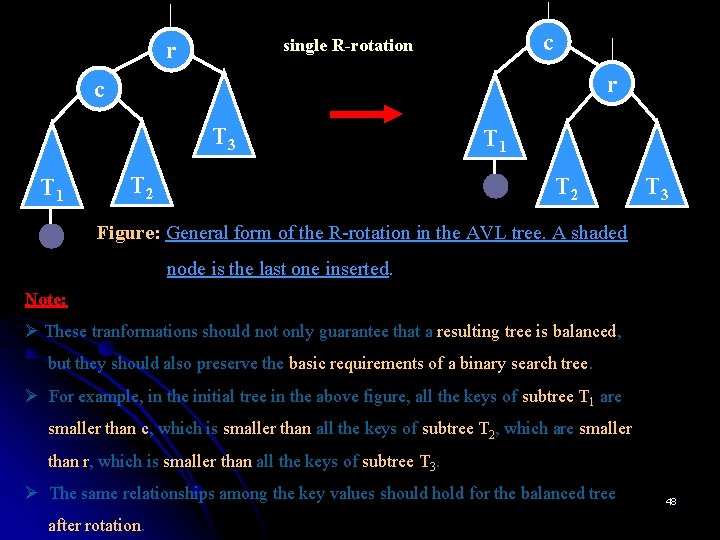
c single R-rotation r r c T 3 T 1 T 2 T 3 Figure: General form of the R-rotation in the AVL tree. A shaded node is the last one inserted. Note: Ø These tranformations should not only guarantee that a resulting tree is balanced, but they should also preserve the basic requirements of a binary search tree. Ø For example, in the initial tree in the above figure, all the keys of subtree T 1 are smaller than c, which is smaller than all the keys of subtree T 2, which are smaller than r, which is smaller than all the keys of subtree T 3. Ø The same relationships among the key values should hold for the balanced tree after rotation. 48

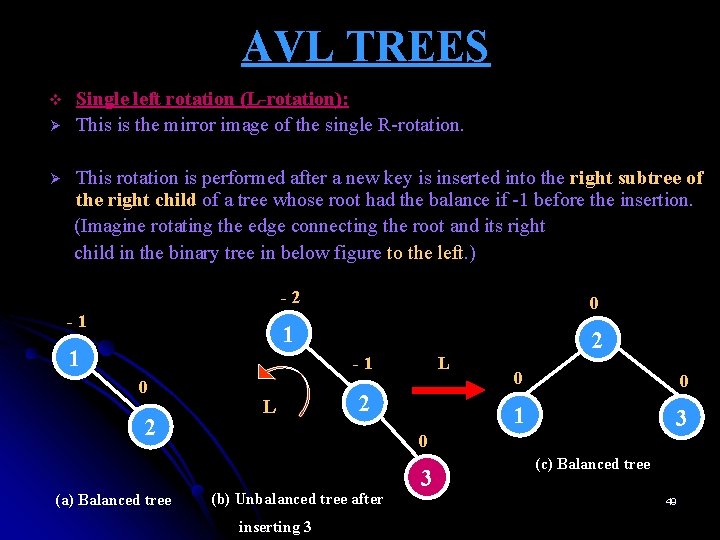
AVL TREES v Ø Ø Single left rotation (L-rotation): This is the mirror image of the single R-rotation. This rotation is performed after a new key is inserted into the right subtree of the right child of a tree whose root had the balance if -1 before the insertion. (Imagine rotating the edge connecting the root and its right child in the binary tree in below figure to the left. ) -1 1 -2 0 1 2 -1 0 2 (a) Balanced tree L L 2 0 0 1 3 0 (b) Unbalanced tree after inserting 3 3 (c) Balanced tree 49

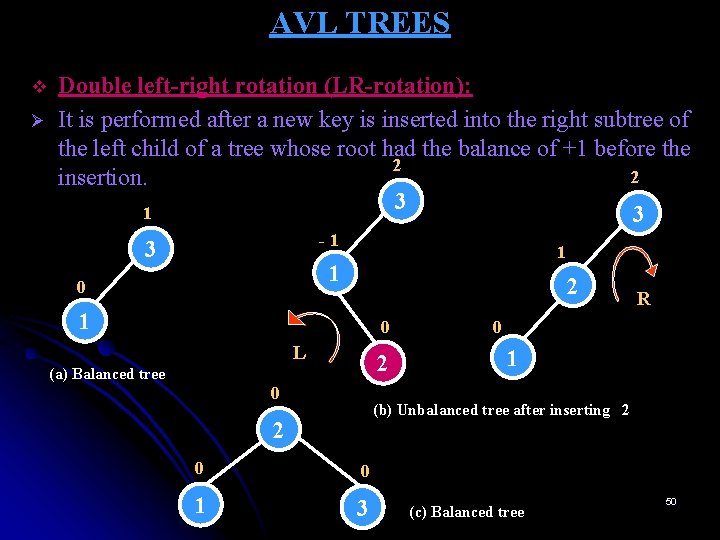
AVL TREES v Ø Double left-right rotation (LR-rotation): It is performed after a new key is inserted into the right subtree of the left child of a tree whose root had the balance of +1 before the 2 2 insertion. 3 1 3 -1 3 1 1 0 2 R 1 0 0 L 2 (a) Balanced tree 0 1 (b) Unbalanced tree after inserting 2 2 0 0 1 3 (c) Balanced tree 50

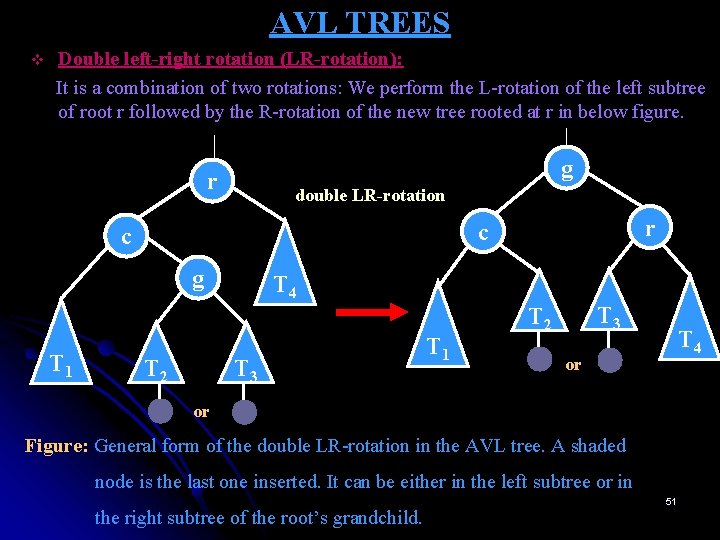
AVL TREES v Double left-right rotation (LR-rotation): It is a combination of two rotations: We perform the L-rotation of the left subtree of root r followed by the R-rotation of the new tree rooted at r in below figure. g r double LR-rotation g T 1 r c c T 2 T 4 T 3 T 1 T 3 T 2 T 4 or or Figure: General form of the double LR-rotation in the AVL tree. A shaded node is the last one inserted. It can be either in the left subtree or in the right subtree of the root’s grandchild. 51

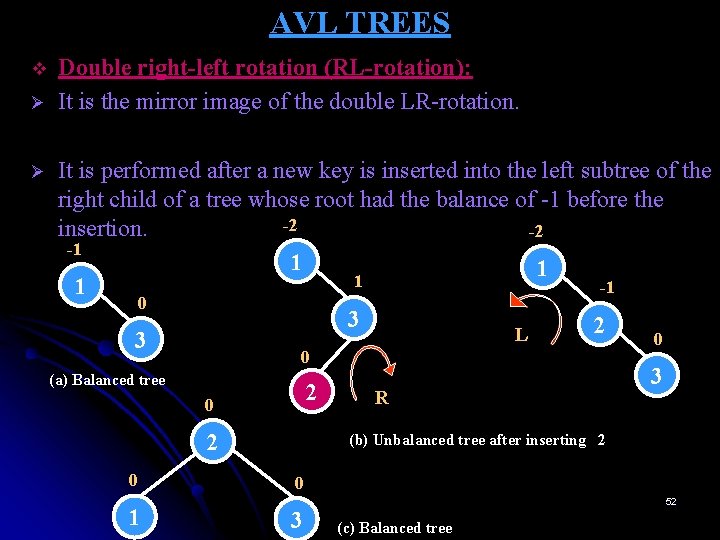
AVL TREES v Ø Ø Double right-left rotation (RL-rotation): It is the mirror image of the double LR-rotation. It is performed after a new key is inserted into the left subtree of the right child of a tree whose root had the balance of -1 before the -2 insertion. -2 -1 1 0 3 2 L 0 3 (a) Balanced tree 2 R 0 2 0 1 (b) Unbalanced tree after inserting 2 0 3 52 (c) Balanced tree

AVL TREES Ø The balance factor of a node is 0 if and only if the height of the left subtree and height of right subtree are same. Ø The balance factor of a node is 1 if the height of the left subtree is one more than height of right subtree (left heavy). Ø The balance factor of a node is -1 if the height of the right subtree is one more than height of left subtree (right heavy). Ø The height of empty tree is -1. Ø If there are several nodes with the ± 2 balance, the rotation is done for the tree rooted at the unbalanced node that is the closest to the newly inserted leaf. 53

Construction of an AVL tree EXAMPLE 1: 100, 200, 300, 250, 270, 40 Step 1: Element 100 is inserted into the empty tree as shown below: 0 100 Step 2: Element 200 is inserted to the right of 100 as shown below: -1 100 0 200 54

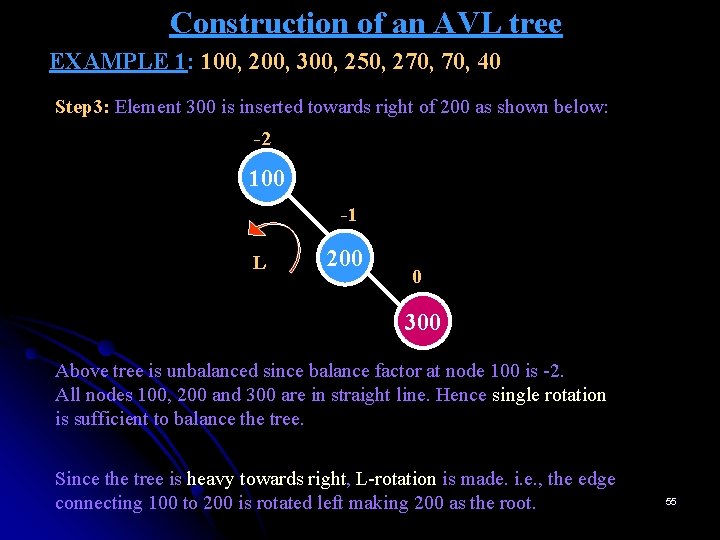
Construction of an AVL tree EXAMPLE 1: 100, 200, 300, 250, 270, 40 Step 3: Element 300 is inserted towards right of 200 as shown below: -2 100 -1 L 200 0 300 Above tree is unbalanced since balance factor at node 100 is -2. All nodes 100, 200 and 300 are in straight line. Hence single rotation is sufficient to balance the tree. Since the tree is heavy towards right, L-rotation is made. i. e. , the edge connecting 100 to 200 is rotated left making 200 as the root. 55

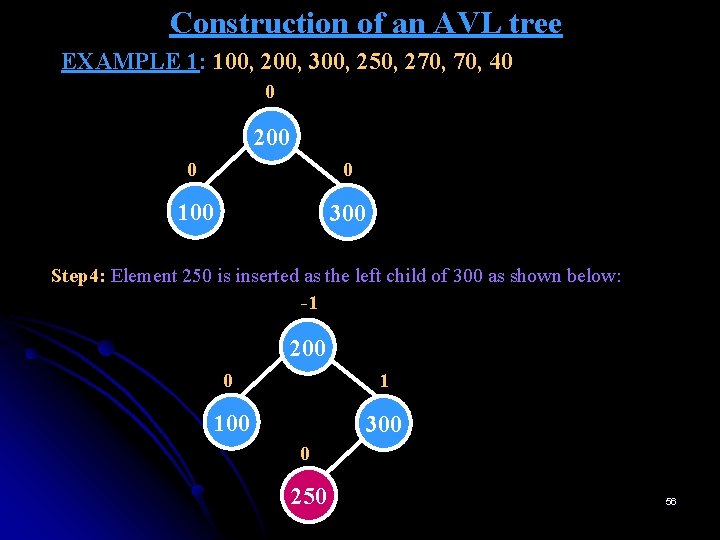
Construction of an AVL tree EXAMPLE 1: 100, 200, 300, 250, 270, 40 0 200 0 0 100 300 Step 4: Element 250 is inserted as the left child of 300 as shown below: -1 200 0 1 100 300 0 250 56

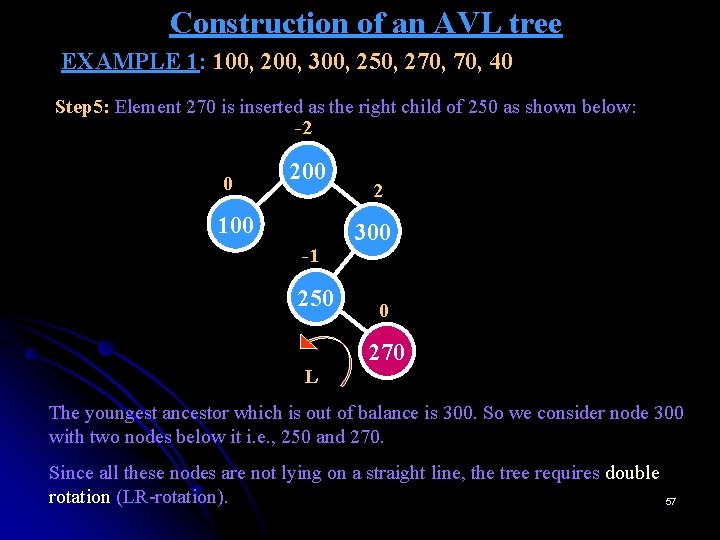
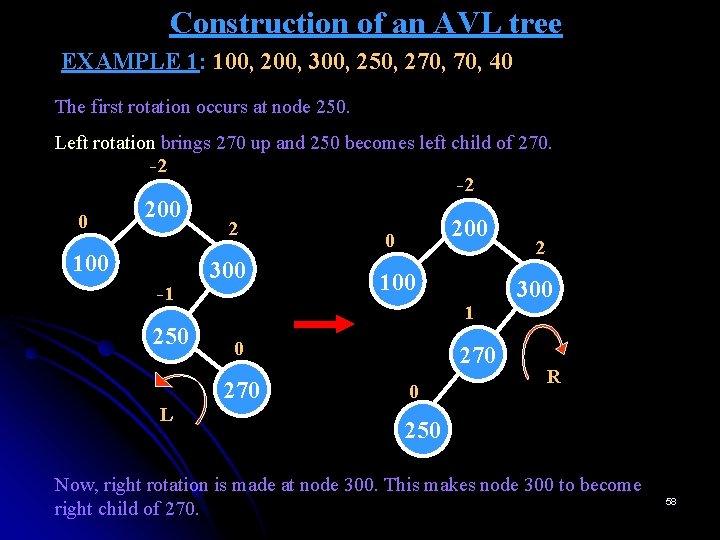
Construction of an AVL tree EXAMPLE 1: 100, 200, 300, 250, 270, 40 Step 5: Element 270 is inserted as the right child of 250 as shown below: -2 0 200 100 -1 250 L 2 300 0 270 The youngest ancestor which is out of balance is 300. So we consider node 300 with two nodes below it i. e. , 250 and 270. Since all these nodes are not lying on a straight line, the tree requires double rotation (LR-rotation). 57

Construction of an AVL tree EXAMPLE 1: 100, 200, 300, 250, 270, 40 The first rotation occurs at node 250. Left rotation brings 270 up and 250 becomes left child of 270. -2 -2 0 200 100 -1 250 L 2 300 200 0 100 1 0 270 0 2 300 R 250 Now, right rotation is made at node 300. This makes node 300 to become right child of 270. 58

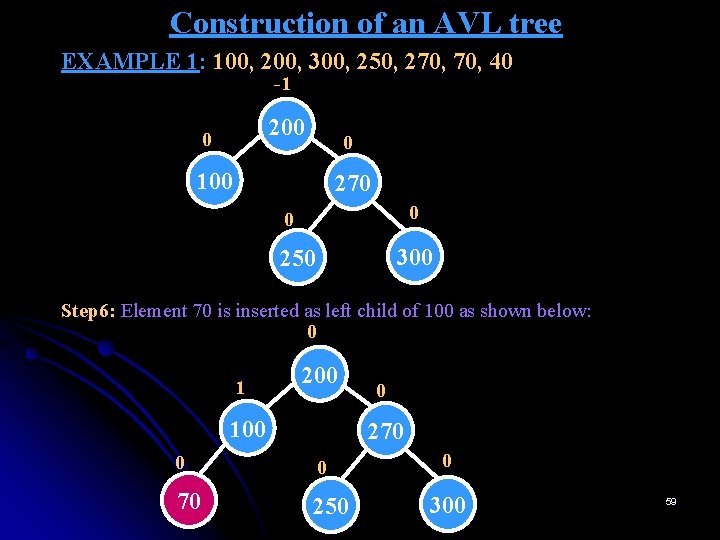
Construction of an AVL tree EXAMPLE 1: 100, 200, 300, 250, 270, 40 -1 200 0 0 100 270 0 0 300 250 Step 6: Element 70 is inserted as left child of 100 as shown below: 0 1 200 100 0 270 0 0 70 250 0 300 59

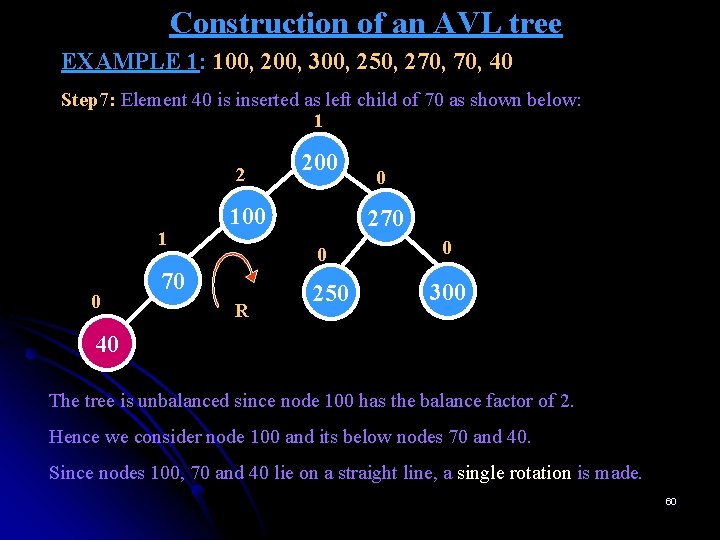
Construction of an AVL tree EXAMPLE 1: 100, 200, 300, 250, 270, 40 Step 7: Element 40 is inserted as left child of 70 as shown below: 1 2 1 0 200 100 270 0 70 R 0 250 0 300 40 The tree is unbalanced since node 100 has the balance factor of 2. Hence we consider node 100 and its below nodes 70 and 40. Since nodes 100, 70 and 40 lie on a straight line, a single rotation is made. 60

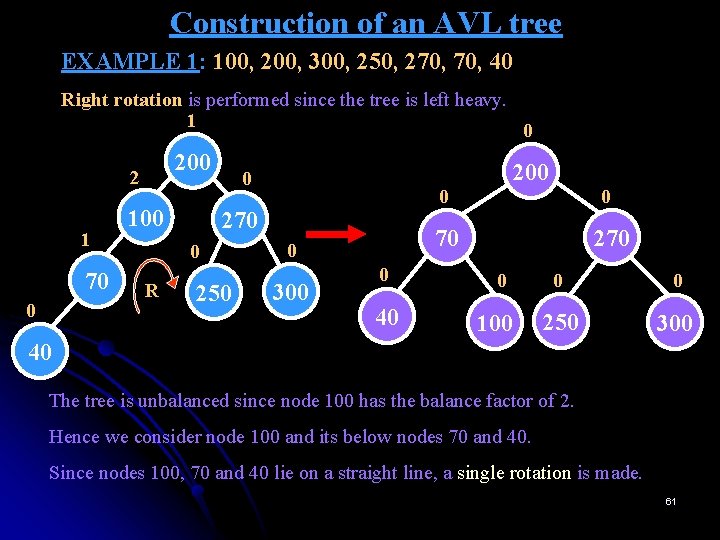
Construction of an AVL tree EXAMPLE 1: 100, 200, 300, 250, 270, 40 Right rotation is performed since the tree is left heavy. 1 0 200 2 1 70 0 100 270 0 R 200 0 250 0 300 0 40 0 0 70 270 0 100 0 0 250 300 40 The tree is unbalanced since node 100 has the balance factor of 2. Hence we consider node 100 and its below nodes 70 and 40. Since nodes 100, 70 and 40 lie on a straight line, a single rotation is made. 61

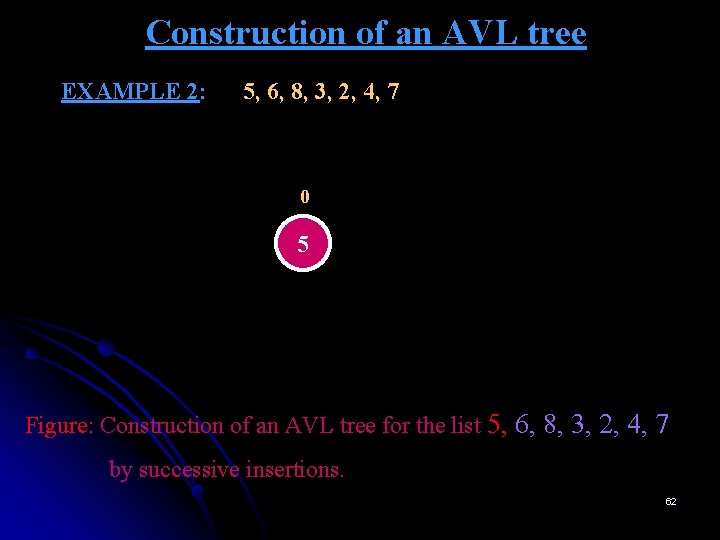
Construction of an AVL tree EXAMPLE 2: 5, 6, 8, 3, 2, 4, 7 0 5 Figure: Construction of an AVL tree for the list 5, 6, 8, 3, 2, 4, 7 by successive insertions. 62

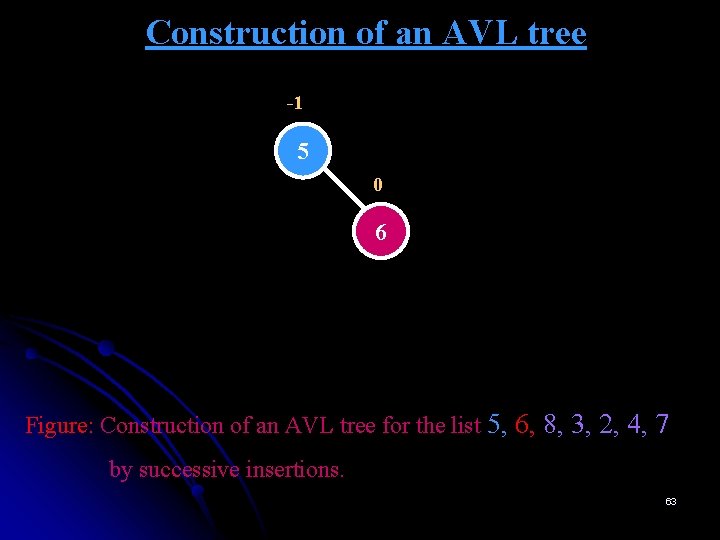
Construction of an AVL tree -1 5 0 6 Figure: Construction of an AVL tree for the list 5, 6, 8, 3, 2, 4, 7 by successive insertions. 63

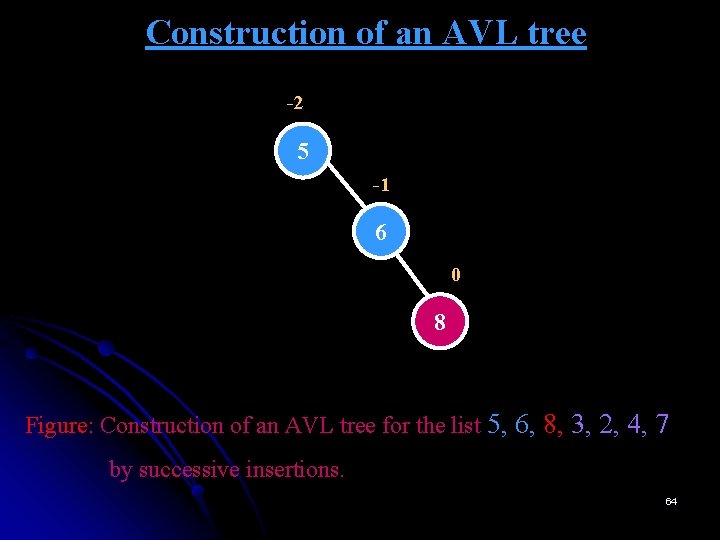
Construction of an AVL tree -2 5 -1 6 0 8 Figure: Construction of an AVL tree for the list 5, 6, 8, 3, 2, 4, 7 by successive insertions. 64

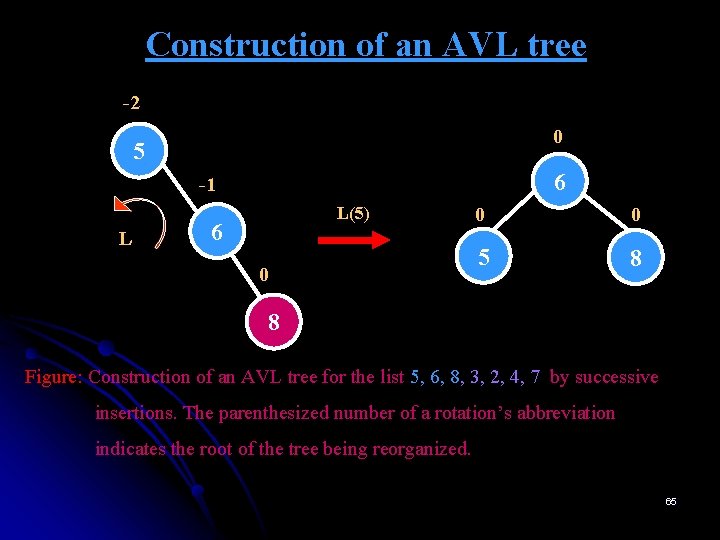
Construction of an AVL tree -2 0 5 6 -1 L L(5) 6 0 0 0 5 8 8 Figure: Construction of an AVL tree for the list 5, 6, 8, 3, 2, 4, 7 by successive insertions. The parenthesized number of a rotation’s abbreviation indicates the root of the tree being reorganized. 65

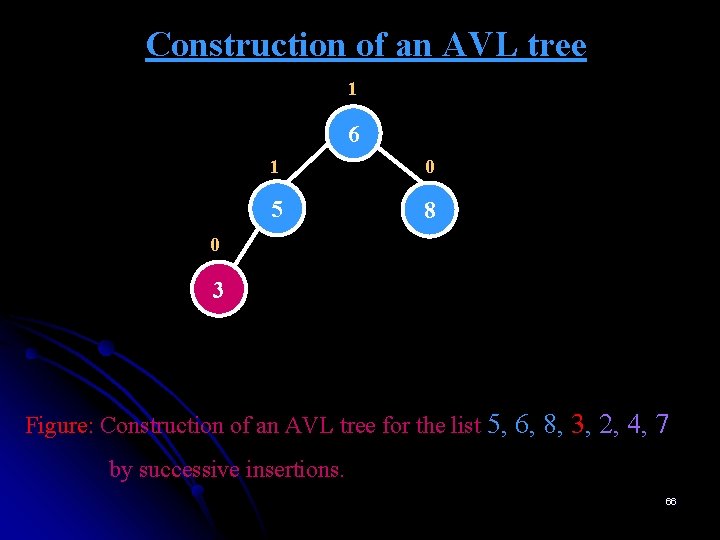
Construction of an AVL tree 1 6 1 0 5 8 0 3 Figure: Construction of an AVL tree for the list 5, 6, 8, 3, 2, 4, 7 by successive insertions. 66

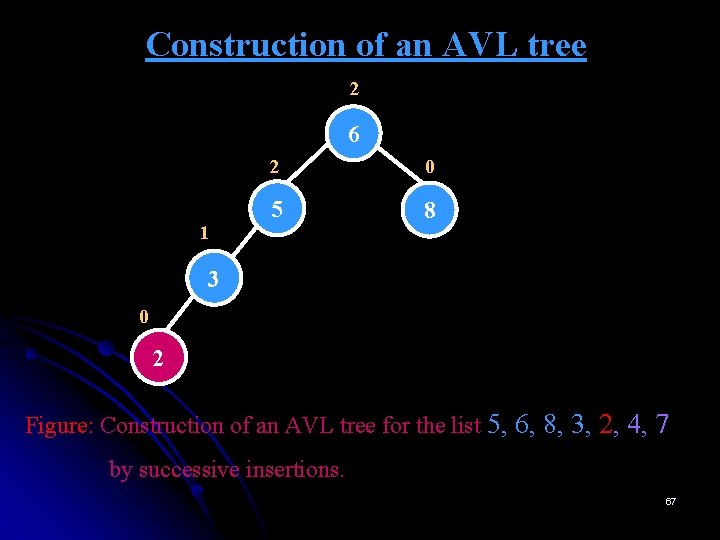
Construction of an AVL tree 2 6 1 2 0 5 8 3 0 2 Figure: Construction of an AVL tree for the list 5, 6, 8, 3, 2, 4, 7 by successive insertions. 67

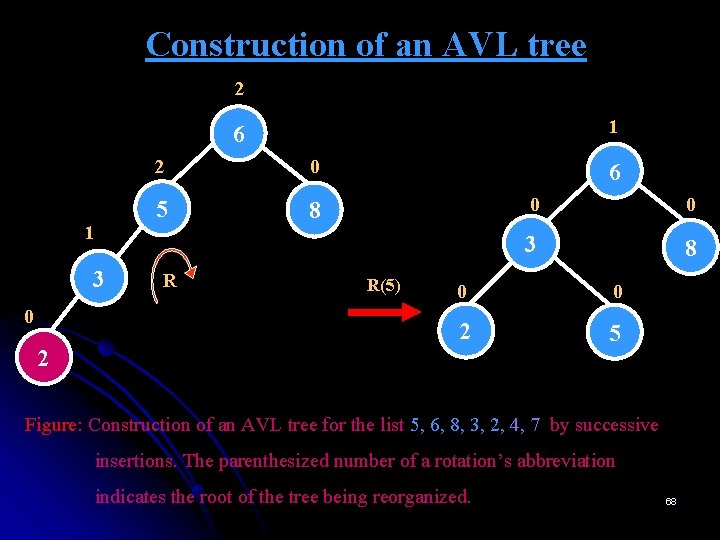
Construction of an AVL tree 2 1 6 1 3 0 2 2 0 5 8 R 6 R(5) 0 0 3 8 0 0 2 5 Figure: Construction of an AVL tree for the list 5, 6, 8, 3, 2, 4, 7 by successive insertions. The parenthesized number of a rotation’s abbreviation indicates the root of the tree being reorganized. 68

Construction of an AVL tree 2 6 -1 0 3 8 0 1 2 5 0 4 Figure: Construction of an AVL tree for the list 5, 6, 8, 3, 2, 4, 7 by successive insertions. 69

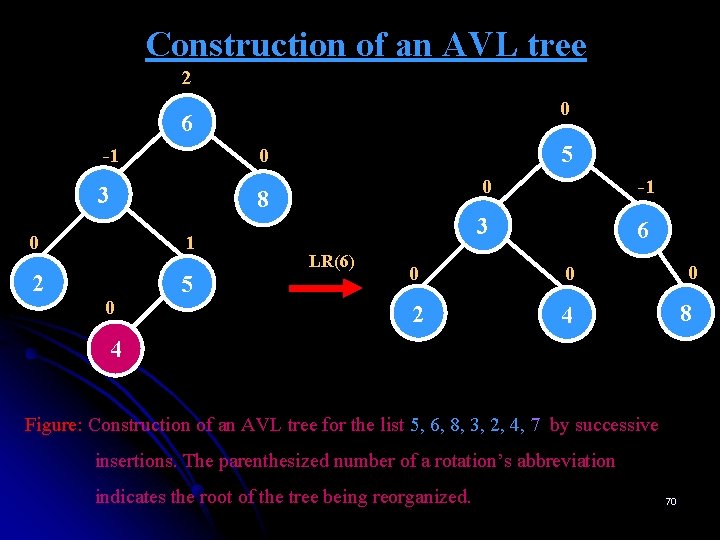
Construction of an AVL tree 2 0 6 -1 0 3 8 0 1 2 5 0 5 LR(6) 0 -1 3 6 0 0 2 4 0 8 4 Figure: Construction of an AVL tree for the list 5, 6, 8, 3, 2, 4, 7 by successive insertions. The parenthesized number of a rotation’s abbreviation indicates the root of the tree being reorganized. 70

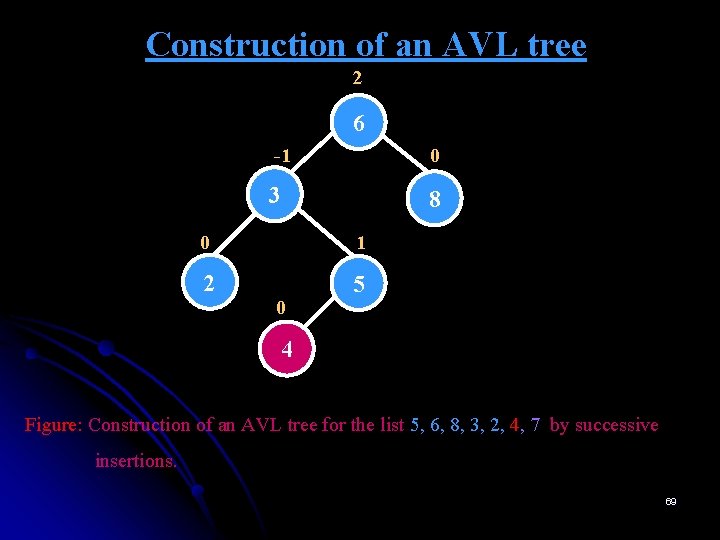
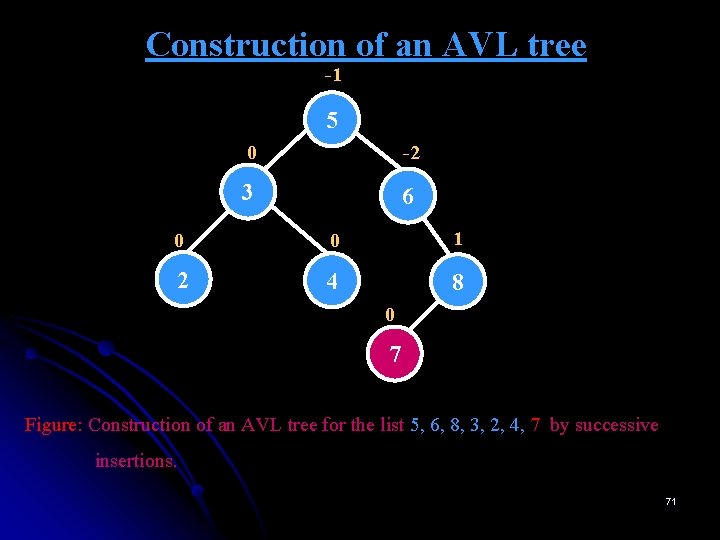
Construction of an AVL tree -1 5 0 -2 3 6 0 0 1 2 4 8 0 7 Figure: Construction of an AVL tree for the list 5, 6, 8, 3, 2, 4, 7 by successive insertions. 71

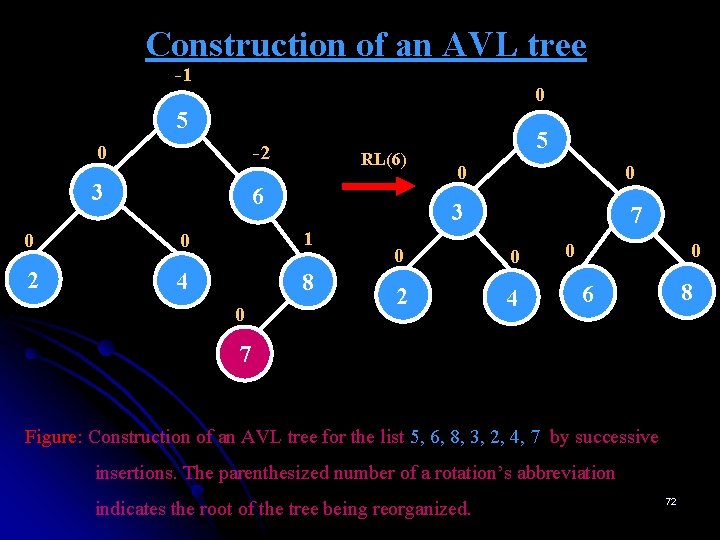
Construction of an AVL tree -1 0 5 0 -2 3 6 RL(6) 0 0 1 2 4 8 0 5 0 0 3 7 0 0 2 4 0 0 8 6 7 Figure: Construction of an AVL tree for the list 5, 6, 8, 3, 2, 4, 7 by successive insertions. The parenthesized number of a rotation’s abbreviation indicates the root of the tree being reorganized. 72

Efficiency of AVL Trees Ø The height h of any AVL tree with n nodes satisfies the inequalities log 2 n ≤ h < 1. 4405 log 2(n + 2) – 1. 3277. Ø These inequalities imply that the operations of searching and insertion are Θ(log n) in the worst case. Ø The operation of key deletion in an AVL tree is considerably more difficult than insertion, but fortunately it turns out to be in the same efficiency class as insertion, i. e. , logarithmic. Ø The drawbacks of AVL trees are frequent rotations, the need to maintain balances for the tree’s nodes, and overall complexity, especially of the deletion operation. Ø These drawbacks have prevented AVL trees from becoming the standard structure for implementing dictionaries. 73

2 -3 TREES Ø Another idea of balancing a search tree is to allow more than one key in the same node ( Ex: 2 -3 trees). Ø 2 -3 trees was introduced by the U. S. computer scientist John Hopcroft in 1970. Ø A 2 -3 tree is a tree that can have nodes of two kinds: 2 -nodes and 3 -nodes. Ø A 2 -node contains a single key K and has two children: the left child serves as the root of a subtree whose keys are less than K and the right child serves as the root of a subtree whose keys are greater than K. 2 - node K <K >K 74

2 -3 TREES Ø A 3 -node contains two ordered keys K 1 and K 2 (K 1 < K 2) and has three children. § The leftmost child serves as the root of a subtree with keys less than K 1 § The middle child serves as the root of a subtree with keys between K 1 and K 2. § The rightmost child serves as the root of a subtree with keys greater than K 2. 3 - node K 1, K 2 < K 1 (K 1, K 2) > K 2 75

2 -3 TREES Ø In 2 -3 trees, all the leaves must be on the same level. i. e. , a 2 -3 tree is always perfectly height-balanced: the length of a path from the root of the tree to a leaf must be the same for every leaf. Ø Searching in a 2 -3 Tree: Searching for an element always starts from the root. If the root is a 2 -node, then the searching is similar to the way we search in a binary search tree: We either stop if search key K is equal to the root’s key or continue the search in the left subtree if K is less than the root’s key or continue the search in the right subtree if K is larger than the root’s key. If the root is a 3 -node, then K can be compared with two elements in the root. If it doesn’t match with root elements, then we need to search either left subtree, or middle subtree or right subtree. If K is less than the first element in the root, continue searching in the left subtree. If K is in between the two elements of root, continue searching in the middle subtree. If K is larger than the second element of the root, continue searching in the right subtree. § § § 76

Creating a 2 -3 Tree Ø Ø Ø Ø If the 2 -3 tree is empty, insert a new key at the root level. Except the first node, rest of the nodes are always inserted in the leaf. By performing a search for the key to be inserted, appropriate leaf node is found. If the leaf is a 2 -node, we insert K there as either the first or the second key, depending on whether K is smaller or larger then the node’s old key. If the leaf is a 3 -node, we split the leaf into two parts: the smallest of the three keys (two old ones and the new key) is put in the first leaf, the largest key is put in the second leaf, while the middle key is promoted to the old leaf’s parent. If the tree’s root itself is the leaf node, a new root is created to accept the middle key. If the promotion of a middle element to its parent leads to a 3 -node, it may be required to split along the chain of leaf’s ancestor. By repeating this procedure, a 2 -3 tree can be constructed. 77

An example of a 2 -3 tree construction is given below: Construct 2 -3 tree for the list 9, 5, 8, 3, 2, 4 and 7 Step 1: Insert the element 9 into the empty tree as shown below: 9 Step 2: Element to be inserted is 5. Since there is only one element in the root node, the element 5 is inserted along with 9 as shown below: 5, 9 Step 3: Element to be inserted is 8. Since 8 is greater than 5 and less than 9, it is inserted between 5 and 9 as shown below: 5, 8, 9 78

An example of a 2 -3 tree construction is given below: Construct 2 -3 tree for the list 9, 5, 8, 3, 2, 4 and 7 Since a node in a 2 -3 tree cannot contain more than 2 elements, we move the middle node to the parent position, left element 5 towards left of the parent and right element 9 towards right of the parent as shown below: 8 5 9 Step 4: Element to be inserted is 3. Since 3 is less than 8, it can be inserted towards left of 8, but along with node 5 as shown below: 8 3, 5 9 79

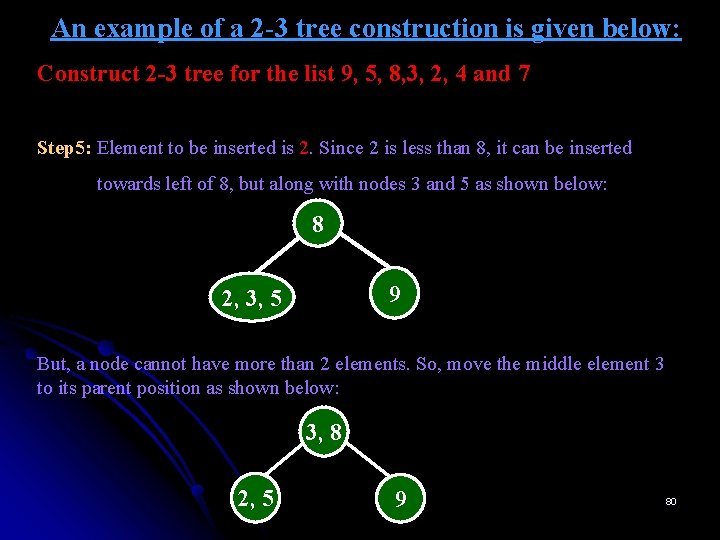
An example of a 2 -3 tree construction is given below: Construct 2 -3 tree for the list 9, 5, 8, 3, 2, 4 and 7 Step 5: Element to be inserted is 2. Since 2 is less than 8, it can be inserted towards left of 8, but along with nodes 3 and 5 as shown below: 8 9 2, 3, 5 But, a node cannot have more than 2 elements. So, move the middle element 3 to its parent position as shown below: 3, 8 2, 5 9 80

An example of a 2 -3 tree construction is given below: Construct 2 -3 tree for the list 9, 5, 8, 3, 2, 4 and 7 But, if a node has two elements i. e. , 3, 8 (except the leaf i. e. , 2, 5), it should have 3 children: left child containing all elements less than 3, middle child containing all elements between 3 and 8, and the right child containing the elements larger than 8. So, the above tree can be modified as shown below: 3, 8 2 5 9 Step 6: Element to be inserted is 4. Since, 4 is between 3 and 8, it can be inserted in the middle node along with 5 as shown below: 3, 8 2 4, 5 9 81

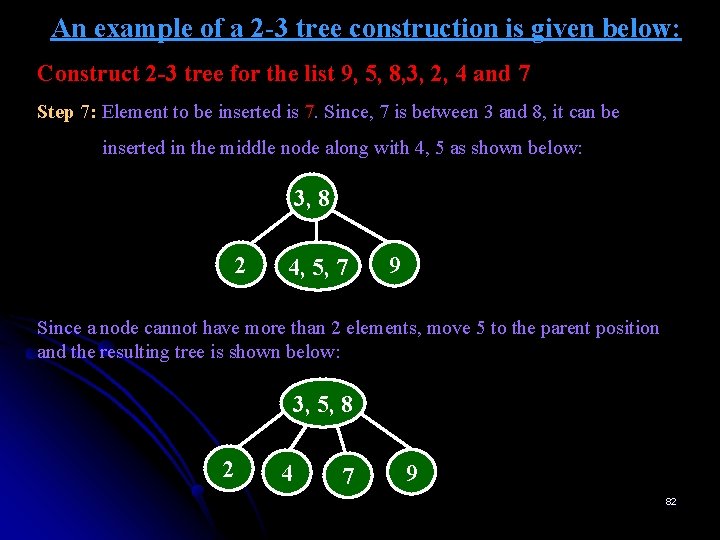
An example of a 2 -3 tree construction is given below: Construct 2 -3 tree for the list 9, 5, 8, 3, 2, 4 and 7 Step 7: Element to be inserted is 7. Since, 7 is between 3 and 8, it can be inserted in the middle node along with 4, 5 as shown below: 3, 8 2 4, 5, 7 9 Since a node cannot have more than 2 elements, move 5 to the parent position and the resulting tree is shown below: 3, 5, 8 2 4 7 9 82

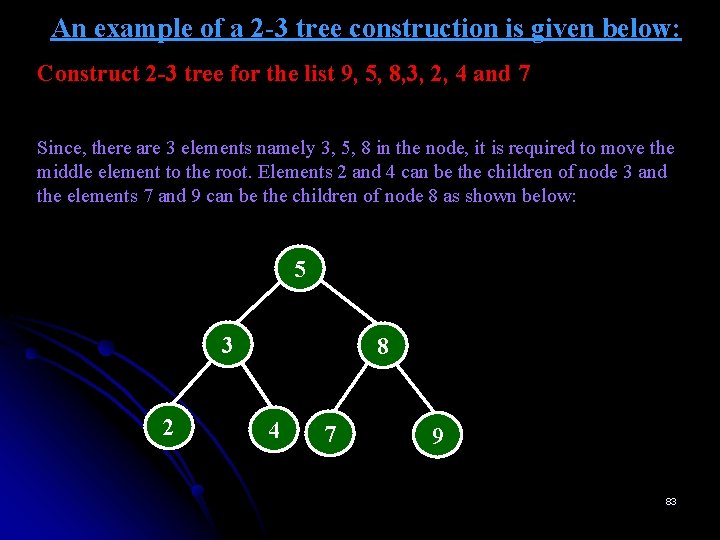
An example of a 2 -3 tree construction is given below: Construct 2 -3 tree for the list 9, 5, 8, 3, 2, 4 and 7 Since, there are 3 elements namely 3, 5, 8 in the node, it is required to move the middle element to the root. Elements 2 and 4 can be the children of node 3 and the elements 7 and 9 can be the children of node 8 as shown below: 5 3 2 8 4 7 9 83

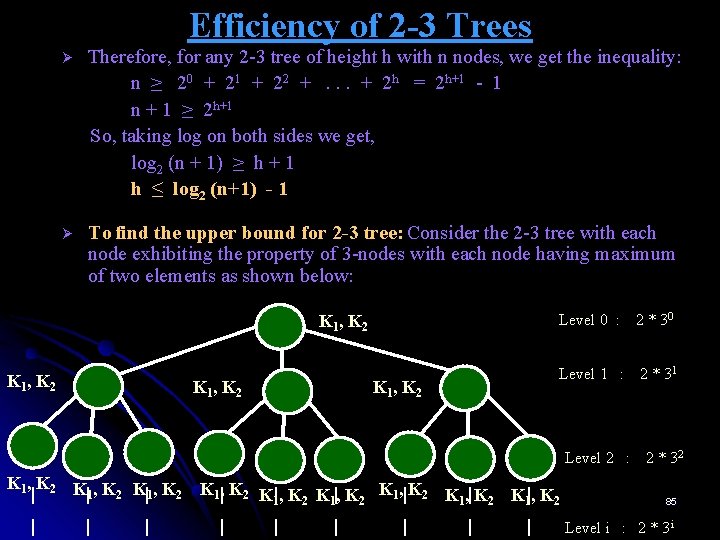
Efficiency of 2 -3 Trees Ø Ø Ø Since a 2 -3 tree is always height balanced, the efficiency of any operation depends only on the height of the tree. To find the time complexity, it is required to find the lower bound as well as the upper bound. To find the lower bound for 2 -3 tree: Consider the 2 -3 tree with each node exhibiting the property of 2 -nodes. Level 0 Number of nodes at level 0 = 1 = 20 Level 1 Number of nodes at level 1 = 21 Level 2 Level i Number of nodes at level 2 = 4 = 22 | | | | Number of nodes at level i = 2 i 84

Efficiency of 2 -3 Trees Ø Therefore, for any 2 -3 tree of height h with n nodes, we get the inequality: n ≥ 20 + 21 + 22 +. . . + 2 h = 2 h+1 - 1 n + 1 ≥ 2 h+1 So, taking log on both sides we get, log 2 (n + 1) ≥ h + 1 h ≤ log 2 (n+1) - 1 Ø To find the upper bound for 2 -3 tree: Consider the 2 -3 tree with each node exhibiting the property of 3 -nodes with each node having maximum of two elements as shown below: Level 0 : 2 * 30 K 1 , K 2 Level 1 : 2 * 31 K 1 , K 2 Level 2 : 2 * 32 K 1 , K 2 K , K | |1 2 | | | K 1|, K 2 K| , K K |, K K 1, | K 2 K , | K K |, K 1 2 1 2 | | | 85 Level i : 2 * 3 i

Efficiency of 2 -3 Trees Ø Therefore, for any 2 -3 tree of height h with n nodes, we get the inequality: n ≤ 2. 30 + 2. 31 + 2. 32 +. . . + 2. 3 h = 2( 30 + 31 + 32 + 3 h) = 3 h+1 - 1 n + 1 ≤ 3 h+1 So, taking log on both sides we get, log 3 (n + 1) ≤ h + 1 h ≥ log 3 (n+1) - 1 Ø These lower and upper bounds on height h, log 3 (n + 1) – 1 ≤ h ≤ log 2 ( n + 1) - 1, imply that the time efficiencies of searching, insertion, and deletion are all in Θ (log n) in both the worst and average case. 86

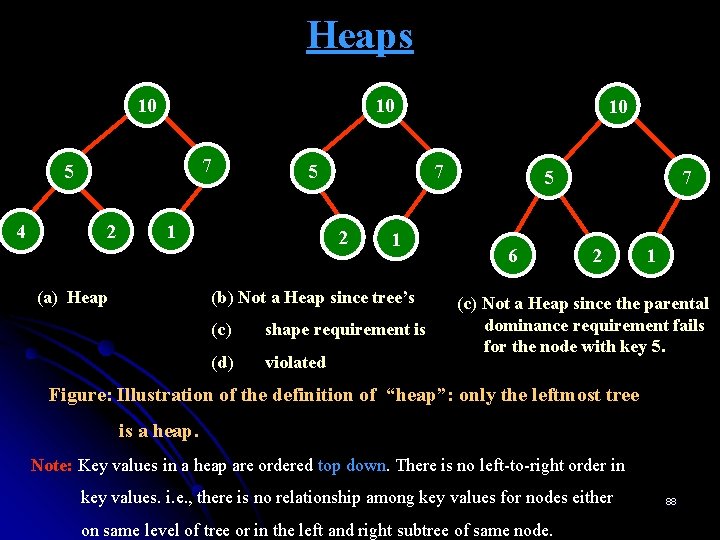
Heaps Ø A heap is a special type of data structure which is suitable for implementing priority queue (Using priority queue, elements can be inserted into queue based on the priority and elements can be deleted from the queue based on the priority) and also suitable for important sorting technique called heap sort. Ø DEFINITION: A heap can be defined as a binary tree with keys assigned to its nodes (one key per node) provided the following two conditions are met: 1. The tree’s shape requirement - the binary tree is almost complete or complete. i. e. , all its levels are full except possibly the last level, where only some rightmost leaves may be missing. 2. The parental dominance requirement - the key at each node is greater than or equal to the keys at its children. 87

Heaps 10 10 7 5 4 2 5 1 7 2 1 (b) Not a Heap since tree’s (a) Heap 10 (c) shape requirement is (d) violated 5 6 7 2 1 (c) Not a Heap since the parental dominance requirement fails for the node with key 5. Figure: Illustration of the definition of “heap”: only the leftmost tree is a heap. Note: Key values in a heap are ordered top down. There is no left-to-right order in key values. i. e. , there is no relationship among key values for nodes either on same level of tree or in the left and right subtree of same node. 88

Important properties of Heaps Ø Ø There exists exactly one almost complete binary tree with n nodes. Its height is equal to log 2 n. The root of a heap always contains its largest element. A node of a heap considered with all its descendants is also a heap. A heap can be implemented as an array by recording its elements in the topdown, left-to-right fashion. It is convenient to store the heap’s elements in positions 1 through n of such an array, leaving H[0] unused. In such a representation, a) the parental node keys will be in the first n/2 positions of the array, while the leaf keys will occupy the last n/2 positions; b) the children of a key in the array’s parental position i (1 ≤ i ≤ n/2 ) will be in positions 2 i and 2 i + 1, and correspondingly, the parent of a key in position i ( 2 ≤ i ≤ n) will be in position i/2. 0 10 5 4 7 2 1 1 2 3 4 5 6 10 5 7 4 2 1 Parents leaves Array Representation of heap shown in figure. 89

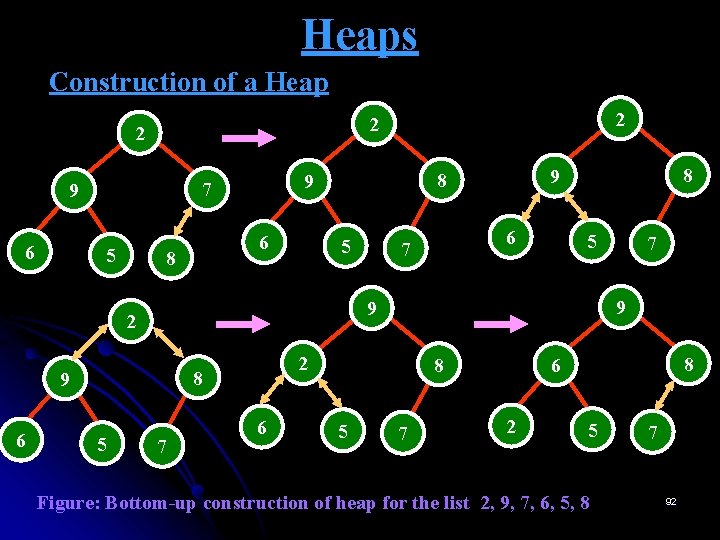
Heaps Ø Thus, we could also define a heap as an array H[1. . . n] in which every element in position i in the first half of the array is greater than or equal to the elements in positions 2 i and 2 i + 1, i. e. , H[i] ≥ max{ H[2 i], H[2 i + 1]} for i = 1, . . . , n/2. Construction of a Heap Bottom-up heap construction algorithm: Ø It initializes the almost complete binary tree with n nodes by placing keys in the order given and then “heapifies” the tree as follows: Ø Starting with the last parental node, the algorithm checks whether the parental dominance holds for the key at this node. Ø If it doesn, t, the algorithm exchanges the node’s key K with the larger key of its children and checks whether the parental dominance holds for K in its new position. 90

Heaps Construction of a Heap Bottom-up heap construction algorithm: Ø This process continues until the parental dominance requirement for K is satisfied. Ø After completing the “heapification” of the subtree rooted at the current parental node, the algorithm proceeds to do the same for the node’s immediate predecessor. Ø The algorithm stops after this is done for the tree’s root. 91

Heaps Construction of a Heap 2 5 6 8 5 7 9 2 8 9 5 5 9 2 6 6 7 8 9 7 9 6 2 2 7 8 6 2 5 Figure: Bottom-up construction of heap for the list 2, 9, 7, 6, 5, 8 7 92

ALGORITHM Heap. Bottom. Up (H[1. . . n]) //Constructs a heap from the elements of a given array //by the bottom-up algorithm 2 //Input: An array H[1. . . n] of orderable items //Output: A heap H[1. . . n] 7 9 for i ← n/2 downto 1 do k ← i; v ← H[k] 6 5 heap ← false 8 while not heap and 2 * k ≤ n do j ← 2*k if j < n //there are two children if H[j] < H[j + 1] j ← j + 1 if v ≥ H[j] 0 1 2 3 4 5 6 heap ← true 2 9 7 6 5 8 else H[k] ← H[j]; k ← j H[k] ← v Parents leaves 93

Efficiency of Bottom-up algorithm in the worst case: Ø Assume, for simplicity, that n = 2 k - 1 so that a heap’s tree is full, i. e. , the maximum number of nodes occurs on each level. Ø Let h be the height of the tree, where h= log 2 n Ø Each key on level i of the tree will traverse to the leaf level h in the worst case of the heap construction algorithm. Ø Since moving to next level down requires two comparisons – one to find the larger child and the other to determine whether the exchange is required, the total number of key comparisons involving a key on level i will be 2(h – i). Ø Therefore, the total number of key comparisons in the worst case will be h -1 Cworst(n) = ∑ i=0 h-1 ∑ 2(h – i) = ∑ 2(h-i) 2 i = 2 (n – log 2 (n + 1)) level i keys i=0 Thus, with this bottom-up algorithm, a heap of size n can be constructed with fewer than 2 n comparisons. 94

Construction of a Heap Ø The alternative (and less efficient) algorithm constructs a heap by successive insertions of a new key into a previously constructed heap. It is called as topdown heap construction algorithm. Ø To insert a new key K into a heap, first attach a new node with key K in it after the last leaf of the existing heap. Ø Then shift K up to its appropriate place in the new heap as follows: • Compare K with its parent’s key: if the latter is greater than or equal to K, stop ; otherwise, swap these two keys and compare K with its new parent. • This swapping continues until K is not greater than its last parent or it reaches the root. Ø Since the height of a heap with n nodes is about log 2 n, the time efficiency of insertion is in O(log n). 95

9 6 2 6 8 5 10 9 7 10 2 5 7 9 6 10 8 2 5 7 8 Figure: Inserting a key (10) into the heap. The new key is shifted up via a swap with its parent until it is not larger than its parent ( or is in the root). 96

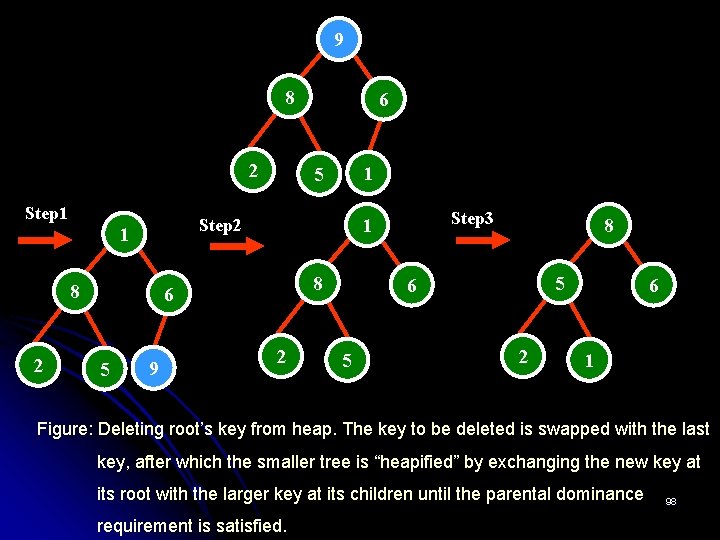
Deletion from a Heap Ø Consider the deletion of the root’s key. Maximum Key Deletion from heap Step 1 Exchange the root’s key with the last key K of the heap. Step 2 Decrease the heap’s size by 1. Step 3 “Heapify” the smaller tree by shifting K down the tree exactly in the same way we did it in the bottom-up heap construction algorithm. i. e. , verify the parental dominance for K: if it holds, we are done; if not, swap K with the larger of its children and repeat this operation until the parental dominance condition holds for K in its new position. Ø The efficiency of deletion is determined by the number of key comparisons needed to “heapify” the tree after swap has been made and size of the tree is decreased by 1. The time efficiency of deletion is in O(log n) as well. 97

9 8 2 Step 1 8 9 Step 3 1 8 6 5 1 5 Step 2 1 2 6 2 8 5 6 5 2 6 1 Figure: Deleting root’s key from heap. The key to be deleted is swapped with the last key, after which the smaller tree is “heapified” by exchanging the new key at its root with the larger key at its children until the parental dominance requirement is satisfied. 98

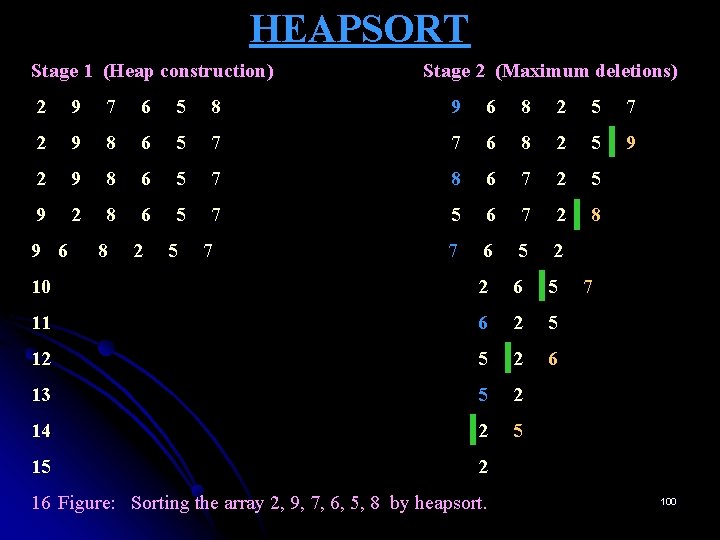
HEAPSORT Ø This sorting algorithm was discovered by J. W. Williams. This is a two-stage algorithm that works as follows: Stage 1 (Heap construction): Construct a heap for a given array. Stage 2 (Maximum deletions): Apply the root-deletion operation n-1 times to the remaining heap. Ø Ø As a result, the array elements are eliminated in decreasing order. Ø But since under the array implementation of heaps, an element being deleted is placed last, the resulting array will be exactly the original array sorted in ascending order. 99

HEAPSORT Stage 1 (Heap construction) Stage 2 (Maximum deletions) 2 9 7 6 5 8 9 6 8 2 5 7 2 9 8 6 5 7 7 6 8 2 5 9 2 9 8 6 5 7 8 6 7 2 5 9 2 8 6 5 7 5 6 7 2 8 7 6 5 2 10 2 6 5 11 6 2 5 12 5 2 6 13 5 2 14 2 5 15 2 9 6 8 2 5 7 16 Figure: Sorting the array 2, 9, 7, 6, 5, 8 by heapsort. 7 100

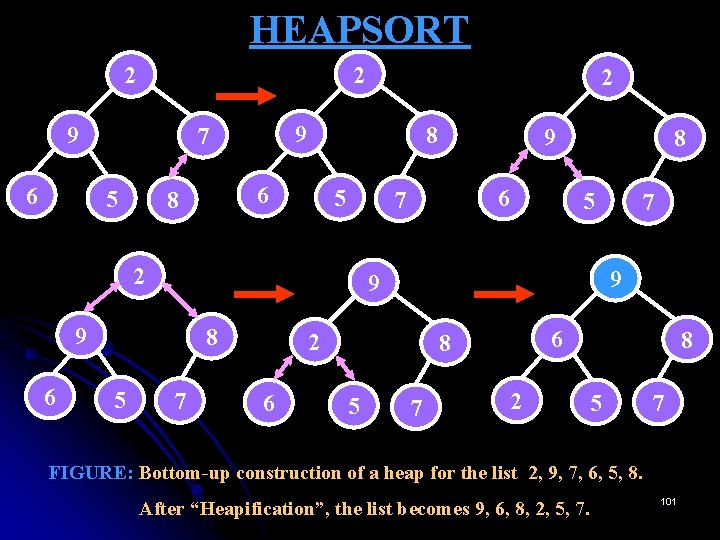
HEAPSORT 2 2 9 6 9 7 5 8 6 8 5 8 7 2 6 6 8 5 7 9 9 9 5 9 7 2 6 2 7 2 8 5 7 FIGURE: Bottom-up construction of a heap for the list 2, 9, 7, 6, 5, 8. After “Heapification”, the list becomes 9, 6, 8, 2, 5, 7. 101

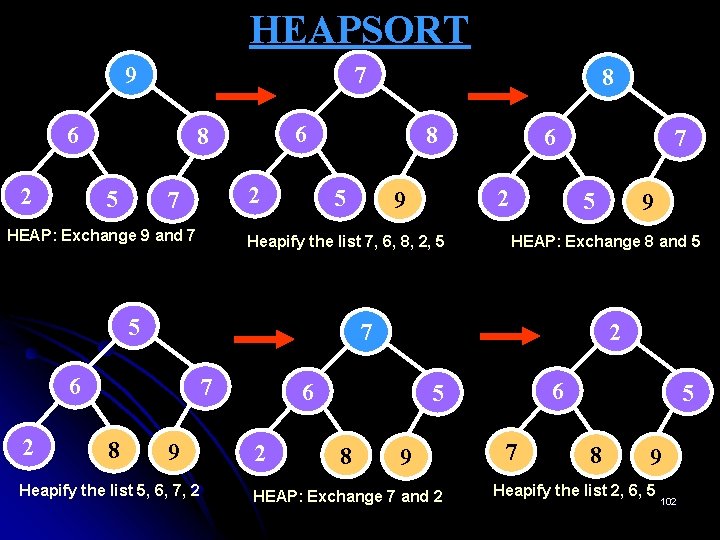
HEAPSORT 7 9 6 2 6 8 5 2 7 HEAP: Exchange 9 and 7 8 5 7 9 2 Heapify the list 5, 6, 7, 2 6 5 8 9 HEAP: Exchange 8 and 5 7 6 8 6 2 9 Heapify the list 7, 6, 8, 2, 5 5 2 8 9 HEAP: Exchange 7 and 2 7 5 8 9 Heapify the list 2, 6, 5 102

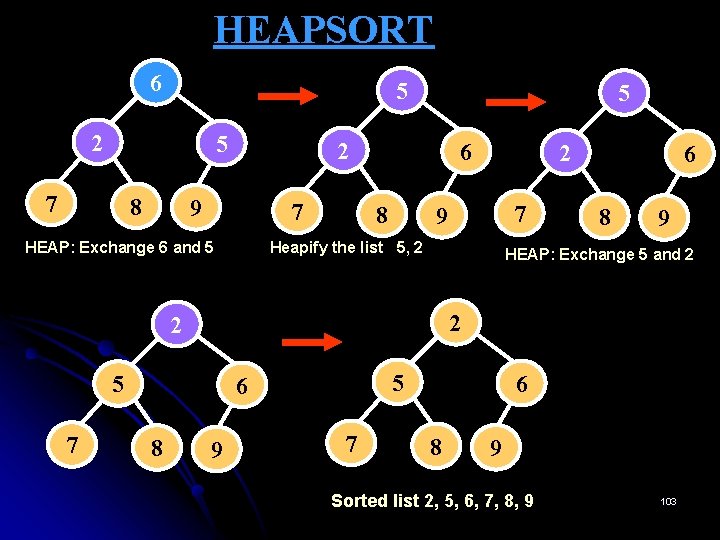
HEAPSORT 6 5 2 5 7 8 5 2 9 7 HEAP: Exchange 6 and 5 6 8 Heapify the list 5, 2 6 8 9 HEAP: Exchange 5 and 2 2 5 5 6 8 7 9 2 7 2 9 7 6 8 9 Sorted list 2, 5, 6, 7, 8, 9 103

Analysis of Heapsort using bottom-up approach Ø The heap construction stage of the algorithm is in O(n). Ø Now, it is required to analyze only the second stage. • Observe that after exchanging the root with (n-1)th item, we have to reconstruct the heap for (n-1) elements which depends only on height of the tree. • • So, time complexity to reconstruct the heap for (n-1) elements = 2 log 2(n-1) After exchanging 0 th item with n-2 item, time complexity to reconstruct the heap = 2 log 2 (n-2) After exchanging 0 th item with n-3 item, time complexity to reconstruct the heap = 2 log 2 (n-3). . . After exchanging 0 th item with 1 st item, time complexity to reconstruct the heap = 2 log 2 1 104

Analysis of Heapsort using bottom-up approach Ø So, the total time complexity T(n) is given by the inequality: T(n) ≤ 2 log 2 (n-1) + 2 log 2 (n-2) + 2 log 2 (n-3) +. . . + 2 log 2 1 n-1 T(n) ≤ 2 ∑ log 2 i ≤ 2 ∑ log 2 (n-1) which indicates that log 2 (n-1) i=1 appears (n-1) times. Therefore, the time complexity for the second stage = 2 n log 2 n ≈ n log 2 n. Ø So, the time complexity of heap sort =time complexity of stage 1 + time complexity of stage 2 = O(n) + O(n log 2 n) = O(max{ n, n log 2 n }) = O(n log 2 n) Therefore, the time complexity of heapsort = O(nlog 2 n) 105

End of Chapter 6 106