Simple Recursive Algorithms A short list of categories

Simple Recursive Algorithms

A short list of categories n Algorithm types we will consider include: n n n n Simple recursive algorithms Backtracking algorithms Divide and conquer algorithms Dynamic programming algorithms Greedy algorithms Branch and bound algorithms Brute force algorithms Randomized algorithms 2

Simple recursive algorithms n A simple recursive algorithm: n n Solves the base cases directly Recurs with a simpler subproblem or subproblems May do some extra work to convert the solution to the simpler subproblem into a solution to the given problem I call these “simple” because several of the other algorithm types are inherently recursive 3

Some example algorithms n We will look briefly at the following simple recursive algorithms: n n n n Factorial All permutations Tree traversal Flood fill Quicksort Towers of Hanoi Ackermann’s function We will also consider the equivalence of loops and recursion 4

Factorial n The factorial function is the “Hello World” of recursion n n The problem with this example is that it can be done almost as easily with a loop (so why bother learning recursion? ) n n public static long factorial(int n) { if (n <= 1) return 1; else return n * factorial(n - 1); } public static long factorial(int n) { int result = 1; while (n > 1) { result *= n; n--; } } In the following slides, we look at some example problems for which recursion really is simpler 5

Permutations n n n A permutation of a set of objects is a particular ordering of those objects When we speak of “all permutations” of a set, we mean all possible ways of ordering those objects Examples: n n n Given the empty set { }, the only possible permutation is { } Given the set {A}, the only possible permutation is {A} Given the set {A, B}, the possible permutations are {AB, BA} Given the set {A, B, C}, the possible permutations are {ABC, ACB, BAC, BCA, CAB, CBA} Etc. 6

Finding all permutations of n objects n To find all permutations of n objects: n n n Find all permutations of n-1 of those objects Insert the remaining object into all possible positions of each permutation of n-1 objects Example: To find all permutations of 3 objects {A, B, C} n n n Find all permutations of 2 of the objects, say B and C: B C and C B Insert the remaining object, A, into all possible positions (marked by ^) in each of the permutations of B and C: and ^ B ^ C ^ B ^ ABC BAC BCA ACB CAB CBA 7

A program to find permutations n n We will develop complete Java code to find all permutations of a nonempty String of characters Array. List<String> permutations. Of(String s) { if (s. length() == 1) { // return a new Array. List containing just s } else { // separate the first character from the rest // get all permutations. Of ( the rest of the characters ) // for each permutation, // add the first character in all possible positions, and // put each result into a new Array. List } // return the new Array. List } 8

permutations. Of(String), part I Array. List<String> permutations. Of(String s) { Array. List<String> result = new Array. List<String>(); if (s. length() == 1) { // base case // return a new Array. List containing just s result. add(s); return result; } // continued. . . 9

permutations. Of(String), part II else { // separate the first character from the rest char first = s. char. At(0); String rest = s. substring(1); // get all permutations. Of the rest of the characters Array. List<String> simpler = permutations. Of(rest); // recursive step // for each permutation, for (String permutation : simpler) { // extra work // add the first character in all possible positions, and Array. List additions = insert. All. Positions(first, permutation); // put each result into a new Array. List result. add. All(additions); } return result; } } 10

Insert in all positions n Given one String representing one permutation of n-1 characters, we want to return all permutations resulting from inserting a given character in all n possible positions private Array. List<String> insert. All. Positions(char ch, String s) { Array. List<String> result = new Array. List<String>(); for (int i = 0; i <= s. length(); i++) { String inserted = s. substring(0, i) + ch + s. substring(i); result. add(inserted); } return result; } 11

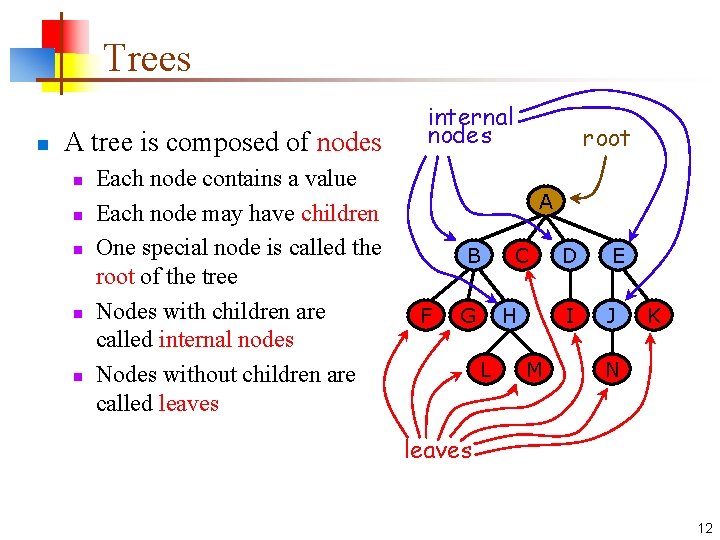
Trees n A tree is composed of nodes n n n Each node contains a value Each node may have children One special node is called the root of the tree Nodes with children are called internal nodes Nodes without children are called leaves internal nodes root A B F G C H L M D E I J K N leaves 12

Tree traversals n n It’s easy to traverse (“walk”) a tree recursively Here’s a recursive method which, if called with the root of a tree, will print out all the values in the tree: n n void print. Tree(Node n) { print the value in node n; for each child c of n, print. Tree(c) Or, in actual Java: void print. Tree(Node n) { System. out. println(n. get. Value()); Iterator iter = node. get. Children(). iterator(); while (iter. has. Next()) { print. Tree(iter. next()); } } n Many data structures are best handled recursively 13

Flood fill n To “flood fill” an area with color old. Color, starting from a particular pixel of color new. Color: n void flood. Fill(Pixel p, Color old. Color, Color new. Color) { if p is not old. Color, just return else { set color of p to new. Color for each pixel q adjacent to p (horizontally or vertically), flood. Fill(q, old. Color, new. Color) } } 14

Quicksort n Quicksort is (in some sense) the fastest sorting algorithm known n n From an array of numbers, pick one to use as a pivot 45 3 17 48 72 25 8 99 14 9 12 21 81 64 33 12 (we’ll use 45 as the pivot) Partition the numbers into those smaller than or equal to the pivot, and those larger than the pivot 3 17 25 8 14 9 12 21 33 12 45 48 72 99 81 64 Now quicksort the left side: And the right side: 3 8 9 12 12 14 17 21 25 33 45 48 64 72 81 99 15

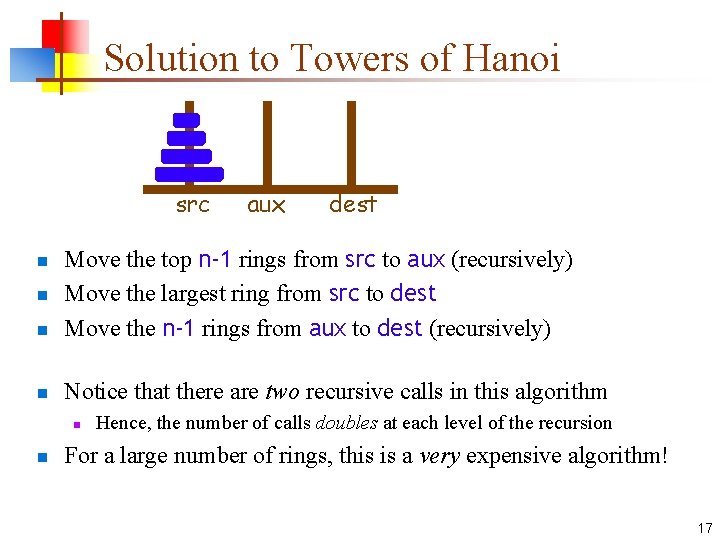
Towers of Hanoi n “Towers of Hanoi” is commonly used as an example of a problem with a simple recursive solution n n n There are three pegs The first (source) peg holds some number of rings You want to move all rings to the last (destination) peg You can only move one ring at a time You can never put a larger ring on top of a smaller ring You have one auxiliary peg you can use src aux dest 16

Solution to Towers of Hanoi src aux dest n Move the top n-1 rings from src to aux (recursively) Move the largest ring from src to dest Move the n-1 rings from aux to dest (recursively) n Notice that there are two recursive calls in this algorithm n n Hence, the number of calls doubles at each level of the recursion For a large number of rings, this is a very expensive algorithm! 17

Ackermann’s function n Ackermann’s function is a deceptively simple little set of equations: n n This can easily be written as a recursive method n n n A(0, y) = y + 1 A(x, 0) = A(x - 1, 1) A(x, y) = A(x - 1, A(x, y - 1)) A(4, 0) = 13 A(4, 1) = 65533 A(4, 2) = 2 65536 -3 After this, the numbers start to get huge quickly This function takes a long time to compute (why? ) 18

Recursion isn’t necessary n n Computers don’t have “recursive hardware”! When a higher-level language is compiled, recursive calls are implemented with a stack n n n When you enter a method, all its local variables (including its formal parameters) are created and put onto a stack The method operates on its own copies of the local variables When the method exits, its local variables are removed from the stack The compiler changes recursive code into nonrecursive code It follows, then, that anything you could do recursively, you could also do nonrecursively by using loops and a stack 19

Tree traversals, again n Here’s a recursive method which, if called with the root of a tree, will print out all the values in the tree: n n void print. Tree(Node n) { print the value in node n; for each child c of n { print. Tree(c) } } Here it is without recursion: n void print. Tree(Node n) { create a new stack s; push n onto s; while (s is not empty) { remove a node m from s and print it push the children of m (if any) onto stack s } } 20

Loops aren’t necessary n n n You can replace any recursion with loops (and a stack for local variables) In addition, you can replace any loop with a recursion For example, consider zeroing out an array: n static void zero. Out(int[] a) { for (int i = 0; i < a. length; i++) a[i] = 0; } Or: n static void zero. Out(int[] a, int n) { // call with n = 0 if (n < a. length) { a[n] = 0; zero. Out(a, n + 1); } } Of course, this is an example, not a proof It can be proved (we won’t do it here) that loops can always be replaced by recursions 21

Closing comments n n n The intent of this set of slides is to get you more familiar with some of the uses of recursion Recursion and loops are, in some sense, equivalent-anything you can do with one, you can do with the other Once you understand recursion, though, it is often simpler to use recursion than to use loops 22

The End 23