Recursive Algorithm Recursive Algorithm Recursive Algorithm UIT 2201

Recursive Algorithm Recursive Algorithm Recursive Algorithm (UIT 2201: Algorithms) Page 1 Leong. HW, So. C, NUS

Examples of recursion… (UIT 2201: Algorithms) Page 2 Leong. HW, So. C, NUS

5. Recursion v A problem solving method of “decomposing bigger problems into smaller sub-problems that are identical to itself. ” v General Idea: o Solve simplest (smallest) cases DIRECTLY uusually these are very easy to solve o Solve bigger problems using smaller sub-problems uthat are identical to itself (but smaller and simpler) v Abstraction: o To solve a given problem, we first assume that we ALREADY know how to solve it for smaller instances!! v Dictionary definition: recursion see recursion (UIT 2201: Algorithms) Page 3 Leong. HW, So. C, NUS

5. Recursion v Dictionary definition: recursion see recursion v Simple Examples from Real Life… o o v TV within a TV 2 parallel mirrors 1 + the previous number “Tomorrow” Recursion Examples from the Web. o Recursive Trees (turtle) – here o Trees and Tower-of-Hanoi – here o Recursion and Biology – here (UIT 2201: Algorithms) Page 4 Leong. HW, So. C, NUS

Example: Fibonacci Numbers… v Definition of Fibonacci numbers 1. F 1 = 1, 2. F 2 = 1, 3. for n>2, Fn = Fn-1 + Fn-2 v Problem: Compute Fn for any n. v The above is a recursive definition. o Fn is computed in-terms of itself o actually, smaller copies of itself – Fn-1 and Fn-2 v Actually, Not difficult: F 3 = 1 + 1 = 2 F 4 = 2 + 1 = 3 F 5 = 3 + 2 = 5 F 6 = 5 + 3 = 8 F 7 = 8 + 5 = 13 F 8 = 13 + 8 = 21 F 9 = 21 + 13 = 34 F 10 = 34 + 21 = 55 F 11 = 55 + 34 = 89 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, … (UIT 2201: Algorithms) Page 5 Leong. HW, So. C, NUS

Fibonacci Numbers: Recursive alg Fibonacci(n) (* Recursive, SLOW *) begin if (n=1) or (n=2) then Fibonacci(n) 1 (*simple case*) else Fibonacci(n) Fibonacci(n-1) + Fibonacci(n-2) endif end; v The v It above is a recursive algorithm is simple to understand elegant! v But, very SLOW (UIT 2201: Algorithms) Page 6 Leong. HW, So. C, NUS

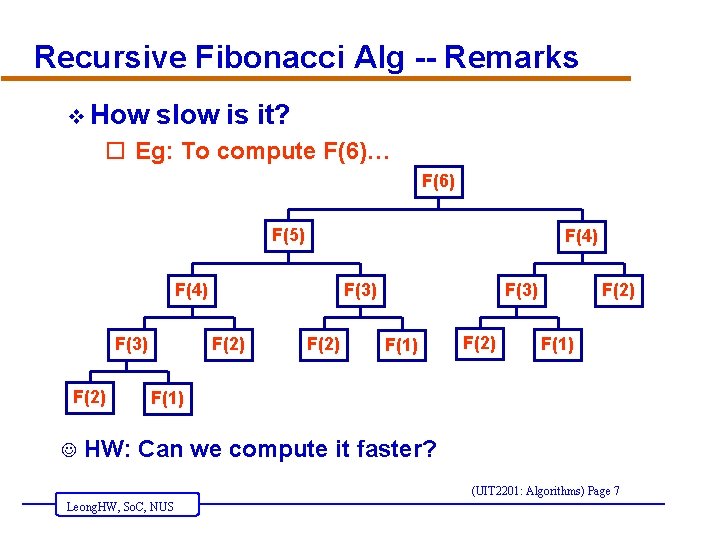
Recursive Fibonacci Alg -- Remarks v How slow is it? o Eg: To compute F(6)… F(6) F(5) F(4) F(3) F(2) J F(3) F(2) F(3) F(1) F(2) F(1) HW: Can we compute it faster? (UIT 2201: Algorithms) Page 7 Leong. HW, So. C, NUS

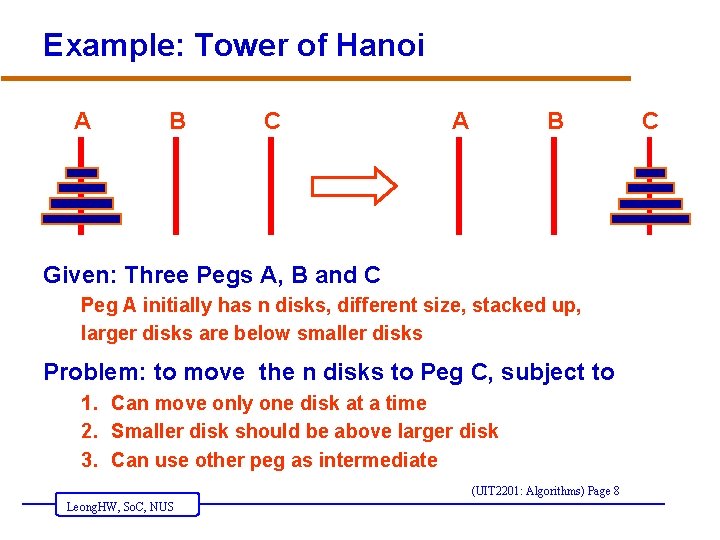
Example: Tower of Hanoi A B C A B Given: Three Pegs A, B and C Peg A initially has n disks, different size, stacked up, larger disks are below smaller disks Problem: to move the n disks to Peg C, subject to 1. Can move only one disk at a time 2. Smaller disk should be above larger disk 3. Can use other peg as intermediate (UIT 2201: Algorithms) Page 8 Leong. HW, So. C, NUS C

Tower of Hanoi v How to Solve: Strategy… o Generalize first: Consider n disks for all n 1 o Our example is only the case when n=4 v Look at small instances… o How about n=1 u Of course, just “Move disk 1 from A to C” o How about n=2? 1. “Move disk 1 from A to B” 2. “Move disk 2 from A to C” 3. “Move disk 1 from B to C” (UIT 2201: Algorithms) Page 9 Leong. HW, So. C, NUS

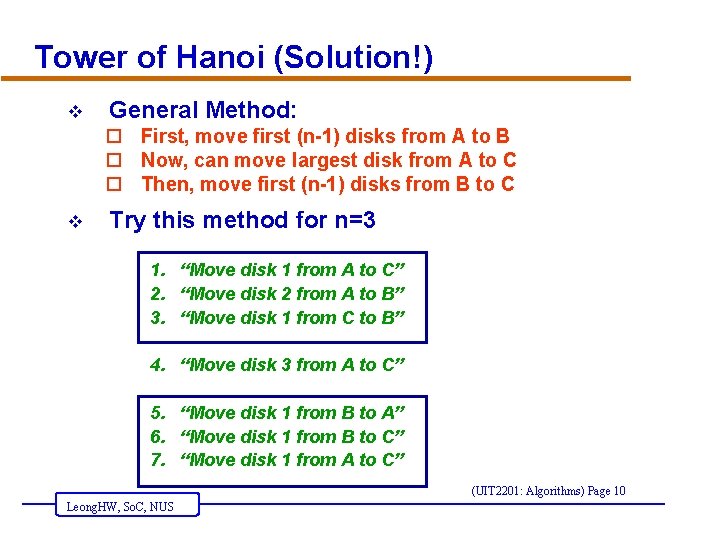
Tower of Hanoi (Solution!) v General Method: o First, move first (n-1) disks from A to B o Now, can move largest disk from A to C o Then, move first (n-1) disks from B to C v Try this method for n=3 1. “Move disk 1 from A to C” 2. “Move disk 2 from A to B” 3. “Move disk 1 from C to B” 4. “Move disk 3 from A to C” 5. “Move disk 1 from B to A” 6. “Move disk 1 from B to C” 7. “Move disk 1 from A to C” (UIT 2201: Algorithms) Page 10 Leong. HW, So. C, NUS

Algorithm for Towel of Hanoi (recursive) v Recursive Algorithm o when (n=1), we have simple case o Else (decompose problem and make recursive-calls) Hanoi(n, A, B, C); (* Move n disks from A to C via B *) begin if (n=1) then “Move top disk from A to C” else (* when n>1 *) Hanoi (n-1, A, C, B); “Move top disk from A to C” Hanoi (n-1, B, C, A); endif end; (UIT 2201: Algorithms) Page 11 Leong. HW, So. C, NUS