Introduction 3 5 Recursive Algorithms Recursive definitions can

Introduction 3. 5 Recursive Algorithms Recursive definitions can be used to describe algorithms as well as functions and sets. (재귀적 정의를 수행한 경우, 손쉽게 알고리즘의 함수/집합으로 기술할 수 있다. ) 예제 1: A procedure to compute an. procedure power(a≠ 0: real, n N) if n = 0 then return 1 else return a · power(a, n− 1) 2 Discrete Mathematics by Yang-Sae Moon

Efficiency of Recursive Algorithms 3. 5 Recursive Algorithms The time complexity of a recursive algorithm may depend critically on the number of recursive calls it makes. (재귀 호출에서의 시간 복잡도는 재귀 호출 횟수에 크게 의존적이다. ) 예제 2: Modular exponentiation to a power n can take log(n) time if done right, but linear time if done slightly differently. (잘하면 O(log(n))이나, 조금만 잘못하면 O(n)이 된다. ) • Task: Compute bn mod m, where m≥ 2, n≥ 0, and 1≤b<m. 3 Discrete Mathematics by Yang-Sae Moon

Modular Exponentiation Algorithm #1 3. 5 Recursive Algorithms Uses the fact that • bn = b·bn− 1 and that • x·y mod m = x·(y mod m) mod m. procedure mpower(b≥ 1, n≥ 0, m>b N) {Returns bn mod m. } if n=0 then return 1; else return (b·mpower(b, n− 1, m)) mod m; Note this algorithm takes (n) steps! 4 Discrete Mathematics by Yang-Sae Moon

Modular Exponentiation Algorithm #2 3. 5 Recursive Algorithms Uses the fact that b 2 k = bk· 2 = (bk)2. procedure mpower(b, n, m) {same signature} if n=0 then return 1 else if 2|n then return mpower(b, n/2, m)2 mod m else return (mpower(b, n− 1, m)·b) mod m (첫 번째 mpower()는 한번 call되고, 그 값을 제곱하는 것임) What is its time complexity? 5 (log n) steps Discrete Mathematics by Yang-Sae Moon

A Slight Variation of Algorithm #2 3. 5 Recursive Algorithms Nearly identical but takes (n) time instead! procedure mpower(b, n, m) {same signature} if n=0 then return 1 else if 2|n then return (mpower(b, n/2, m)·mpower(b, n/2, m)) mod m else return (mpower(b, n− 1, m)·b) mod m The number of recursive calls made is critical. 6 Discrete Mathematics by Yang-Sae Moon

Recursive Euclid’s Algorithm (예제 4) 3. 5 Recursive Algorithms procedure gcd(a, b N) if a = 0 then return b else return gcd(b mod a, a) Note recursive algorithms are often simpler to code than iterative ones… (Recursion이 코드를 보다 간단하게 하지만…) However, they can consume more stack space, if your compiler is not smart enough. (일반적으로, recursion은 보다 많은 stack space를 차지한다. ) 7 Discrete Mathematics by Yang-Sae Moon

Recursion vs. Iteration (1/3) 3. 5 Recursive Algorithms Factorial – Recursion procedure factorial(n N) if n = 1 then return 1 else return n factorial(n – 1) Factorial – Iteration procedure factorial(n N) x : = 1 for i : = 1 to n x : = i x return x 8 Discrete Mathematics by Yang-Sae Moon

Recursion vs. Iteration (2/3) 3. 5 Recursive Algorithms Fibonacci – Recursion procedure fibonacci(n: nonnegative integer) if (n = 0 or n = 1) then return n else return (fibonacci(n– 1) + fibonacci(n– 2)) Fibonacci – Iteration procedure fibonacci(n: nonnegative integer) if n = 0 then return 0 else x : = 0, y : = 1 for i : = 1 to n – 1 z : = x + y, x : = y, y : = z return z 9 Discrete Mathematics by Yang-Sae Moon

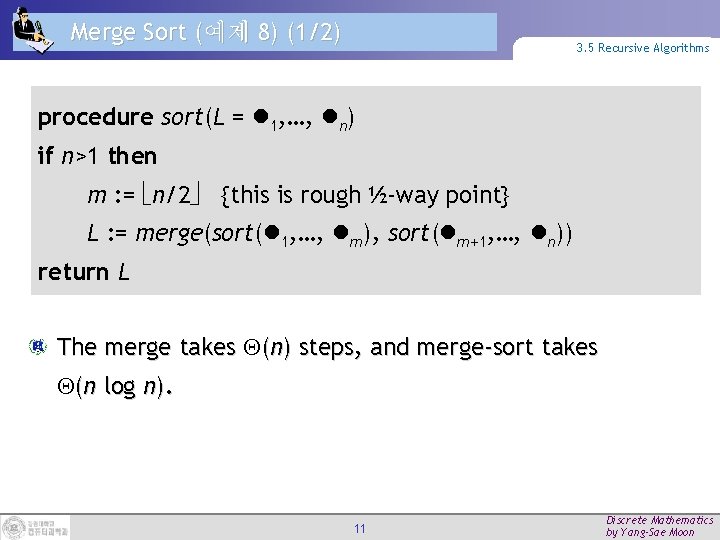
Merge Sort (예제 8) (1/2) 3. 5 Recursive Algorithms procedure sort(L = 1, …, n) if n>1 then m : = n/2 {this is rough ½-way point} L : = merge(sort( 1, …, m), sort( m+1, …, n)) return L The merge takes (n) steps, and merge-sort takes (n log n). 11 Discrete Mathematics by Yang-Sae Moon

Merge Sort (예제 8) (2/2) – skip 3. 5 Recursive Algorithms The Merge Routine procedure merge(A, B: sorted lists) L = empty list i: =0, j: =0, k: =0 while i<|A| j<|B| {|A| is length of A} if i=|A| then Lk : = Bj; j : = j + 1 else if j=|B| then Lk : = Ai; i : = i + 1 else if Ai < Bj then Lk : = Ai; i : = i + 1 else Lk : = Bj; j : = j + 1 k : = k+1 return L 12 Discrete Mathematics by Yang-Sae Moon

Homework #5 3. 5 Recursive Algorithms $3. 1의 연습문제: 1, 3, 32 • A hint for 32: prove it by cases (n = 2 k and n = 2 k + 1) $3. 2의 연습문제: 2(c, d), 9(d, f) $3. 3의 연습문제: 3, 8 $3. 4의 연습문제: 2(a), 8(b) $3. 5의 연습문제: 2, 4 Due Date: 13 Discrete Mathematics by Yang-Sae Moon