Linked List Categories of data structures Data structures

Linked List

Categories of data structures Data structures are categories in two classes – 1. Linear data structure: - organized into sequential fashion - elements are attached one after another - easy to implement because follow the computer memory organization - Traversing is very easy - Examples – array, linked list, stack, queue etc. 2. Non - Linear data structure: -every item is attached with many other items. - data elements are not organized in a sequential fashion - data cannot be traversed in a single run. - Implementation is difficult - Examples – tree, graph etc.

Array vs Linked Lists 1. Access : Random / Sequential Stack elements can be randomly Accessed using Subscript Variable e. g a[0], a[1], a[3] can be randomly accessed While In Linked List We have to Traverse Through the Linked List for Accessing Element. So O(n) Time required for Accessing Element. Generally In linked List Elements are accessed Sequentially. 2. Memory Structure : Stack is stored in contiguous Memory Locations , i. e Suppose first element is Stored at 2000 then Second Integer element will be stored at 2002. But It is not necessary to store next element at the Consecutive memory Location. Element is stored at any available Location , but the Pointer to that memory location is stored in Previous Node.

Array vs Linked Lists 3. Insertion / Deletion As the Array elements are stored in Consecutive memory Locations , so While Inserting elements , we have to create space for Insertion. So More time required for Creating space and Inserting Element Similarly We have to Delete the Element from given Location and then Shift All successive elements up by 1 position In Linked List we have to Just Change the Pointer address field (Pointer), So Insertion and Deletion Operations are quite easy to implement 4. Memory Allocation : Memory Should be allocated at Compile-Time in Stack. i. e at the time when Programmer is Writing Program In Linked list memory can be allocated at Run-Time , i. e After executing Program Stack uses Static Memory Allocation and Linked List Uses Dynamic Memory Allocation Dynamic Memory allocation functions – malloc, calloc etc

Lists Implementation Linear Arrays – Collection of similar elements stored at contiguous memory locations Linked List – Ø Collection of similar data elements stored at discrete memory locations and connected by pointer (link). Hence size can grow or shrink at any point of time. Ø Abstract data type so we will implement only operations Ø Data elements are called nodes Types – 1. Linear linked list or one way list 2. Doubly linked list or two way list 3. Circular linked list 4. Header linked list

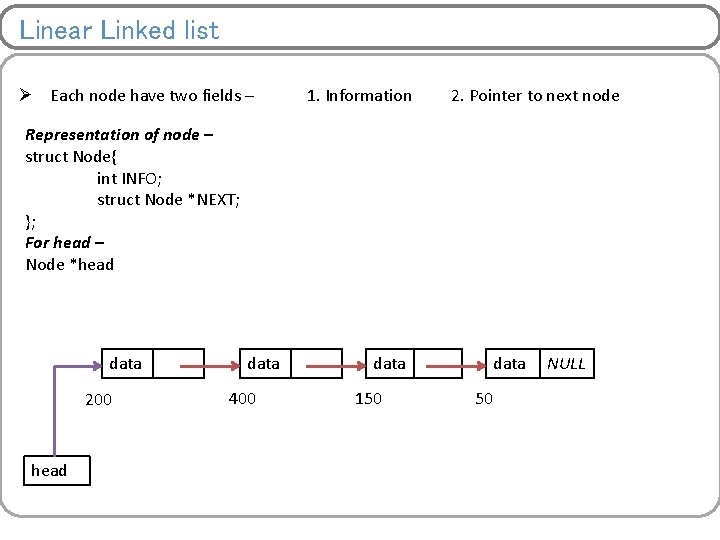
Linear Linked list Ø Each node have two fields – 1. Information 2. Pointer to next node Representation of node – struct Node{ int INFO; struct Node *NEXT; }; For head – Node *head data 200 head data 400 data 150 data 50 NULL

Operations on linear linked list 1. Creating empty linked list 2. Appending nodes to linked list 3. Traversing 4. Insertion 5. Deletion 6. Searching 7. Sorting

Creating a linked list Algorithm Create_List() – This function creates an empty linked list and START is a pointer pointing to created list. 1. Node START 2. START= NULL

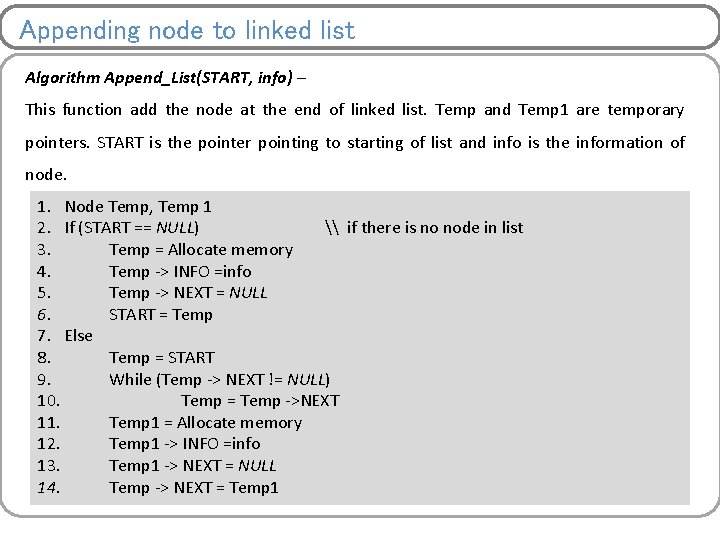
Appending node to linked list Algorithm Append_List(START, info) – This function add the node at the end of linked list. Temp and Temp 1 are temporary pointers. START is the pointer pointing to starting of list and info is the information of node. 1. Node Temp, Temp 1 2. If (START == NULL) \ if there is no node in list 3. Temp = Allocate memory 4. Temp -> INFO =info 5. Temp -> NEXT = NULL 6. START = Temp 7. Else 8. Temp = START 9. While (Temp -> NEXT != NULL) 10. Temp = Temp ->NEXT 11. Temp 1 = Allocate memory 12. Temp 1 -> INFO =info 13. Temp 1 -> NEXT = NULL 14. Temp -> NEXT = Temp 1

Problem Let P be a Quick. Sort Program to sort numbers in ascending order using the first element as pivot. Let t 1 and t 2 be the number of comparisons made by P for the inputs {1, 2, 3, 4, 5} and {4, 1, 5, 3, 2} respectively. Which one of the following holds? A. t 1 = 5 B. t 1 < t 2 C. t 1 > t 2 D. t 1 = t 2 Ans: C When first element or last element is chosen as pivot, Quick Sort's worst case occurs for the sorted arrays. In every step of quick sort, numbers are divided as per the following recurrence. T(n) = T(n-1) + O(n)

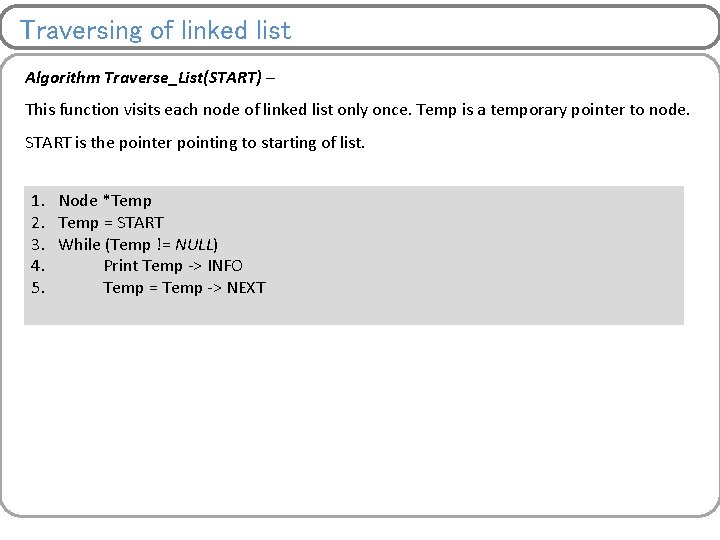
Traversing of linked list Algorithm Traverse_List(START) – This function visits each node of linked list only once. Temp is a temporary pointer to node. START is the pointer pointing to starting of list. 1. 2. 3. 4. 5. Node *Temp = START While (Temp != NULL) Print Temp -> INFO Temp = Temp -> NEXT

Insertion Three ways to insert a node into linked list – 1. Insert at beginning 2. Insert after specified location 3. Insert at the end

Insertion at beginning of linked list Algorithm Insert. Beg_List(START, info) – This function add the node at the starting of linked list. Temp is temporary pointer to node to be inserted into list. START is the pointer pointing to starting of list and info is the information of node. 1. 2. 3. 4. 5. Node Temp = Allocate memory Temp -> INFO =info Temp -> NEXT = START = Temp

Insertion at after specified location of linked list Algorithm Insert. After_List(START, info, Loc) – This function add the node after the specified location of linked list. Temp and Temp 1 are temporary pointers. START is the pointer pointing to starting of list and info is the information of node. Loc is the numbered location after which node is to be inserted. i is a loop variable. 1. Node Temp, Temp 1 2. Temp = START 3. For i=1 to Loc-1 4. Temp = Temp -> NEXT 5. If (Temp == NULL) 6. Exit 7. Temp 1 = Allocate memory 8. Temp 1 -> INFO = info 9. Temp 1 -> NEXT = Temp -> NEXT 10. Temp -> NEXT = Temp 1

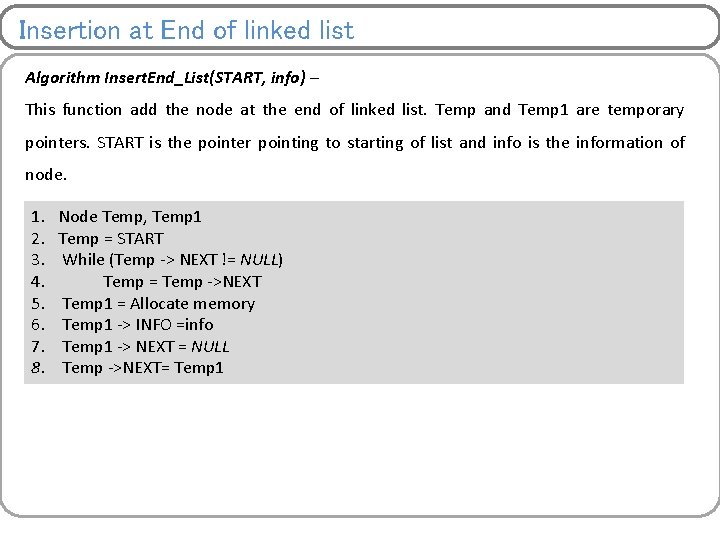
Insertion at End of linked list Algorithm Insert. End_List(START, info) – This function add the node at the end of linked list. Temp and Temp 1 are temporary pointers. START is the pointer pointing to starting of list and info is the information of node. 1. 2. 3. 4. 5. 6. 7. 8. Node Temp, Temp 1 Temp = START While (Temp -> NEXT != NULL) Temp = Temp ->NEXT Temp 1 = Allocate memory Temp 1 -> INFO =info Temp 1 -> NEXT = NULL Temp ->NEXT= Temp 1

Deletion Three ways to insert a node into linked list – 1. Delete from beginning 2. Delete after specified location 3. Delete from the end NOTE: Deletion could be done on the base information (to be deleted) available at any node or not. Here, first find that node and then delete it.

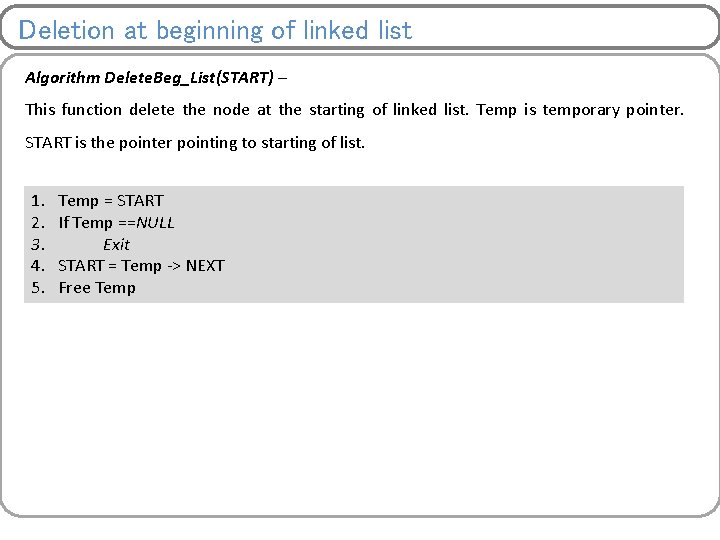
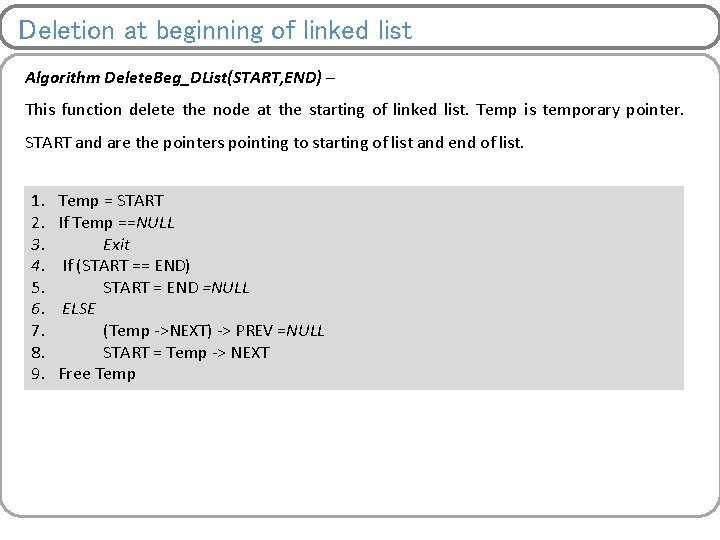
Deletion at beginning of linked list Algorithm Delete. Beg_List(START) – This function delete the node at the starting of linked list. Temp is temporary pointer. START is the pointer pointing to starting of list. 1. 2. 3. 4. 5. Temp = START If Temp ==NULL Exit START = Temp -> NEXT Free Temp

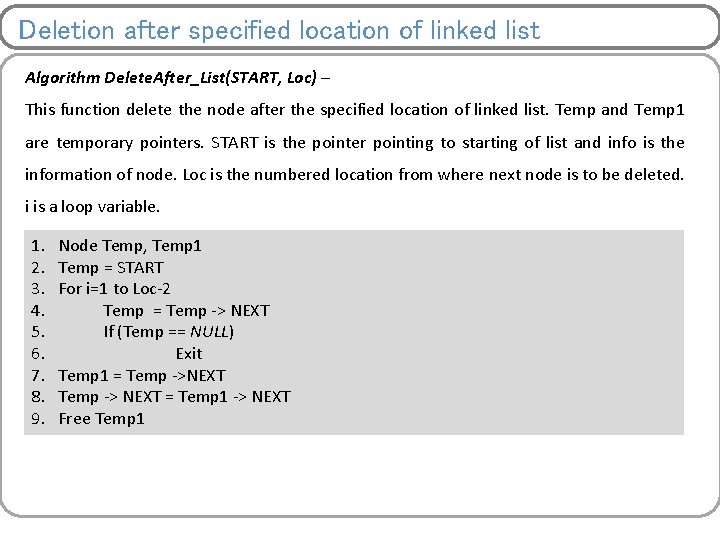
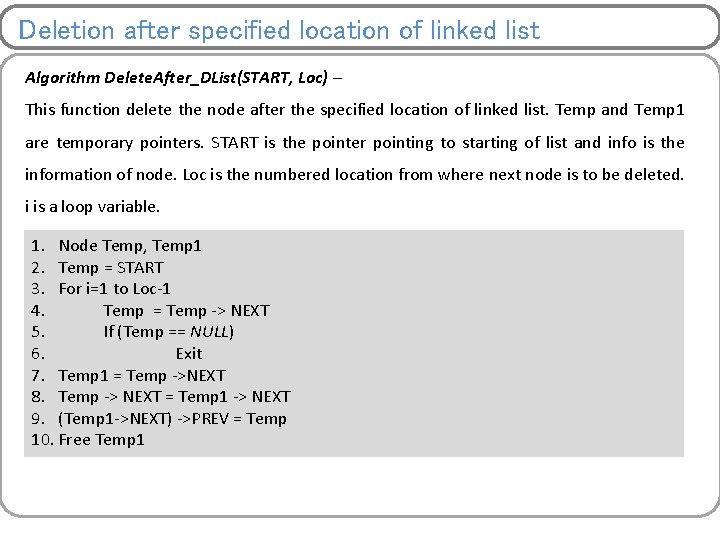
Deletion after specified location of linked list Algorithm Delete. After_List(START, Loc) – This function delete the node after the specified location of linked list. Temp and Temp 1 are temporary pointers. START is the pointer pointing to starting of list and info is the information of node. Loc is the numbered location from where next node is to be deleted. i is a loop variable. 1. 2. 3. 4. 5. 6. 7. 8. 9. Node Temp, Temp 1 Temp = START For i=1 to Loc-2 Temp = Temp -> NEXT If (Temp == NULL) Exit Temp 1 = Temp ->NEXT Temp -> NEXT = Temp 1 -> NEXT Free Temp 1

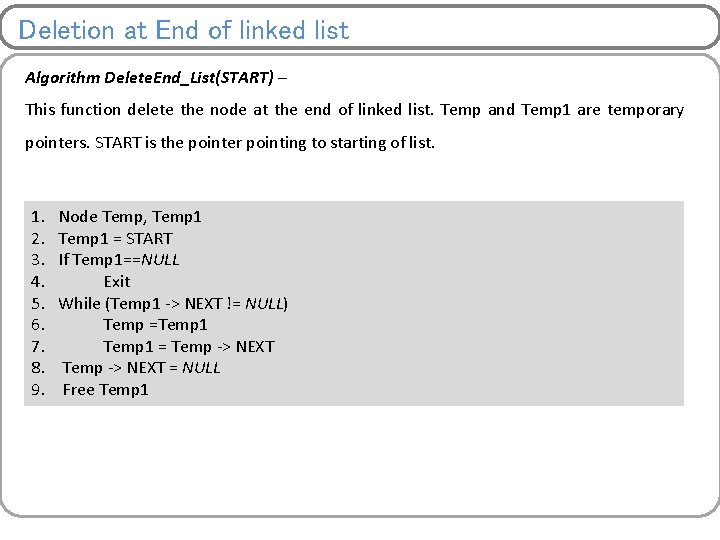
Deletion at End of linked list Algorithm Delete. End_List(START) – This function delete the node at the end of linked list. Temp and Temp 1 are temporary pointers. START is the pointer pointing to starting of list. 1. 2. 3. 4. 5. 6. 7. 8. 9. Node Temp, Temp 1 = START If Temp 1==NULL Exit While (Temp 1 -> NEXT != NULL) Temp =Temp 1 = Temp -> NEXT = NULL Free Temp 1

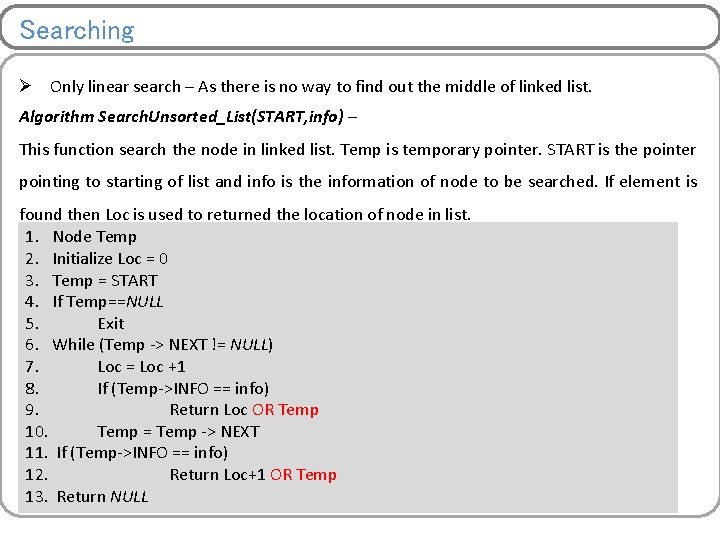
Searching Ø Only linear search – As there is no way to find out the middle of linked list. Algorithm Search. Unsorted_List(START, info) – This function search the node in linked list. Temp is temporary pointer. START is the pointer pointing to starting of list and info is the information of node to be searched. If element is found then Loc is used to returned the location of node in list. 1. Node Temp 2. Initialize Loc = 0 3. Temp = START 4. If Temp==NULL 5. Exit 6. While (Temp -> NEXT != NULL) 7. Loc = Loc +1 8. If (Temp->INFO == info) 9. Return Loc OR Temp 10. Temp = Temp -> NEXT 11. If (Temp->INFO == info) 12. Return Loc+1 OR Temp 13. Return NULL

Algorithm Search. Sorted_List(START, info) – This function search the node in linked list. Temp is temporary pointer. START is the pointer pointing to starting of list and info is the information of node to be searched. If element is found then Loc is used to returned the location of node in list. 1. Node Temp 2. Initialize Loc = 0 3. Temp = START 4. If Temp==NULL 5. Exit 6. While (Temp -> NEXT != NULL) 7. Loc = Loc+1 8. If (Temp->INFO == info) 9. Return Loc OR Temp 10. Else If (Temp->INFO > info) 11. Return NULL 12. Else 13. Temp = Temp ->NEXT 14. If (Temp->INFO == info) 15. Return Loc+1 OR Temp 16. Return NULL

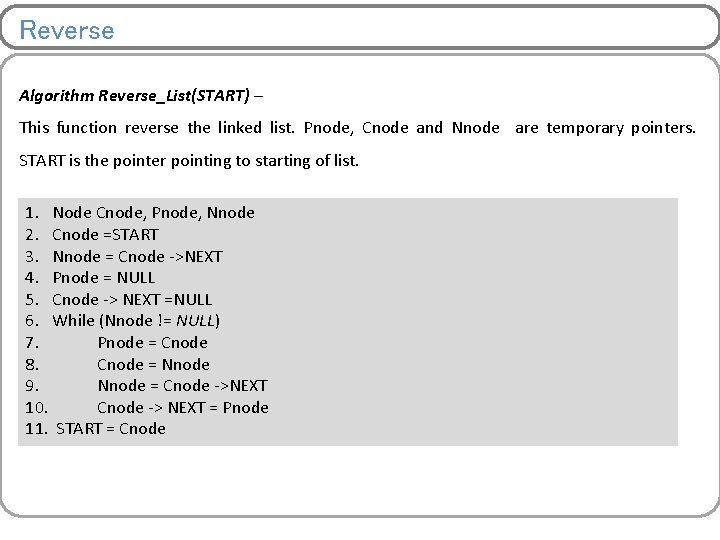
Reverse Algorithm Reverse_List(START) – This function reverse the linked list. Pnode, Cnode and Nnode are temporary pointers. START is the pointer pointing to starting of list. 1. Node Cnode, Pnode, Nnode 2. Cnode =START 3. Nnode = Cnode ->NEXT 4. Pnode = NULL 5. Cnode -> NEXT =NULL 6. While (Nnode != NULL) 7. Pnode = Cnode 8. Cnode = Nnode 9. Nnode = Cnode ->NEXT 10. Cnode -> NEXT = Pnode 11. START = Cnode

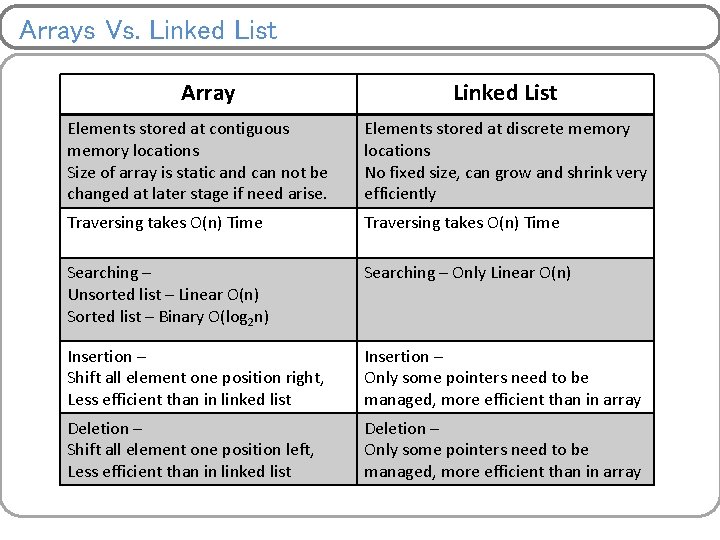
Arrays Vs. Linked List Array Linked List Elements stored at contiguous memory locations Size of array is static and can not be changed at later stage if need arise. Elements stored at discrete memory locations No fixed size, can grow and shrink very efficiently Traversing takes O(n) Time Searching – Unsorted list – Linear O(n) Sorted list – Binary O(log 2 n) Searching – Only Linear O(n) Insertion – Shift all element one position right, Less efficient than in linked list Insertion – Only some pointers need to be managed, more efficient than in array Deletion – Shift all element one position left, Less efficient than in linked list Deletion – Only some pointers need to be managed, more efficient than in array

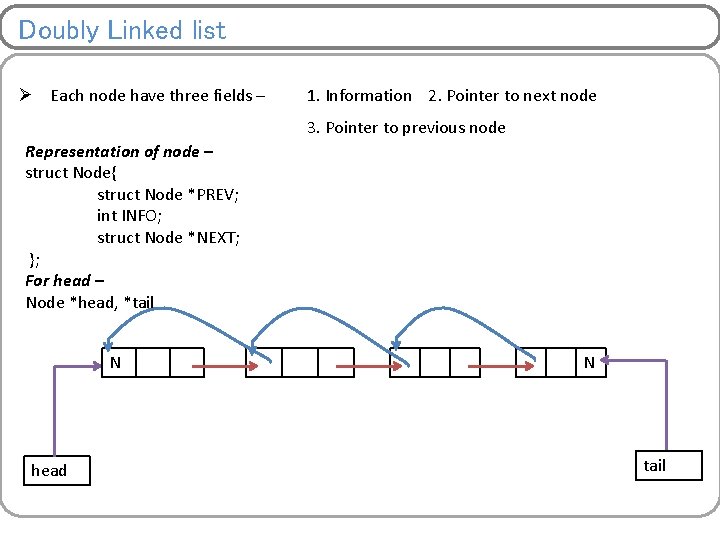
Doubly Linked list Ø Each node have three fields – 1. Information 2. Pointer to next node 3. Pointer to previous node Representation of node – struct Node{ struct Node *PREV; int INFO; struct Node *NEXT; }; For head – Node *head, *tail N head N tail

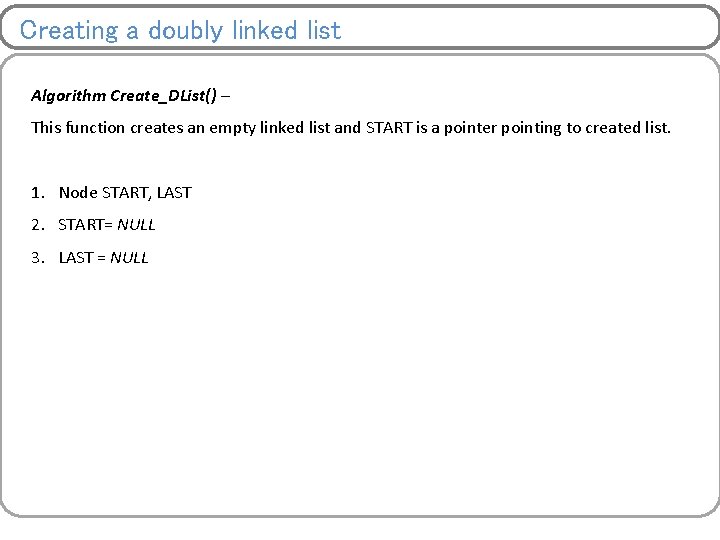
Creating a doubly linked list Algorithm Create_DList() – This function creates an empty linked list and START is a pointer pointing to created list. 1. Node START, LAST 2. START= NULL 3. LAST = NULL

Appending node to Doubly linked list Algorithm Append_DList(START, END, info) – This function add the node at the end of linked list. Temp and Temp 1 are temporary pointers. START and END are the pointers pointing to starting of list and end of list respectively. info is the information of node. 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. 17. 18. Node Temp, Temp 1 If (START == NULL OR END == NULL) Temp = Allocate memory Temp -> INFO =info Temp -> NEXT = NULL Temp -> PREV = NULL START = Temp END = Temp Else Temp = START While (Temp -> NEXT != NULL) Temp = Temp ->NEXT Temp 1 = Allocate memory Temp 1 -> INFO =info Temp 1 -> NEXT = NULL Temp 1 -> PREV = Temp -> NEXT = Temp 1 END = Temp 1 \ if there is no node in list

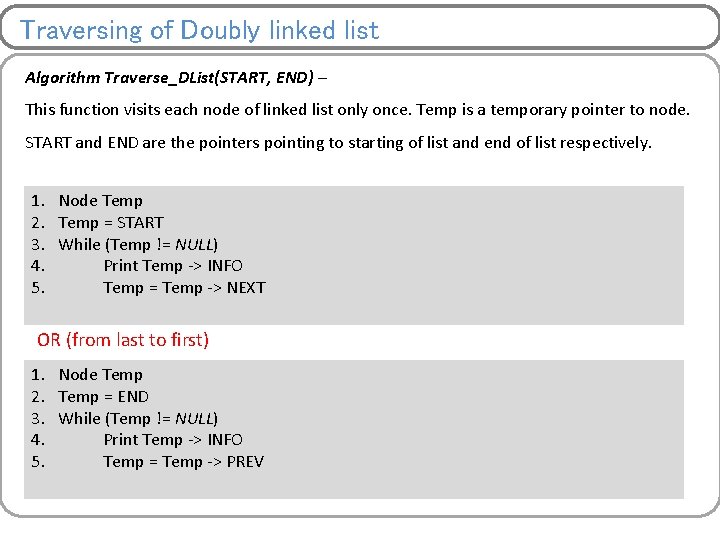
Traversing of Doubly linked list Algorithm Traverse_DList(START, END) – This function visits each node of linked list only once. Temp is a temporary pointer to node. START and END are the pointers pointing to starting of list and end of list respectively. 1. 2. 3. 4. 5. Node Temp = START While (Temp != NULL) Print Temp -> INFO Temp = Temp -> NEXT OR (from last to first) 1. 2. 3. 4. 5. Node Temp = END While (Temp != NULL) Print Temp -> INFO Temp = Temp -> PREV

Insertion Four ways to insert a node into doubly linked list – 1. Insert at beginning 2. Insert after specified location 3. Insert before specified location 4. Insert at the end

Insertion at beginning of Doubly linked list Algorithm Insert. Beg_DList(START, info) – This function add the node at the starting of linked list. Temp is temporary pointer to node to be inserted into list. START is the pointer pointing to starting of list and info is the information of node. 1. 2. 3. 4. 5. 6. 7. Node Temp = Allocate memory Temp -> INFO =info Temp -> NEXT = START Temp ->PREV = NULL START -> PREV= Temp START = Temp

Insertion after specified location of doubly linked list Algorithm Insert. After_DList(START, info, Loc) – This function add the node after the specified location of linked list. Temp and Temp 1 are temporary pointers. START is the pointer pointing to starting of list and info is the information of node. Loc is the numbered location after which node is to be inserted. i is a loop variable. 1. Node Temp, Temp 1 2. Temp = START 3. For i=1 to Loc-1 4. Temp = Temp -> NEXT 5. If (Temp == NULL) 6. Exit 7. Temp 1 = Allocate memory 8. Temp 1 -> INFO = info 9. Temp 1 -> NEXT = Temp -> NEXT 10. Temp 1 ->PREV = Temp 11. (Temp -> NEXT) -> PREV = Temp 1 12. Temp -> NEXT = Temp 1

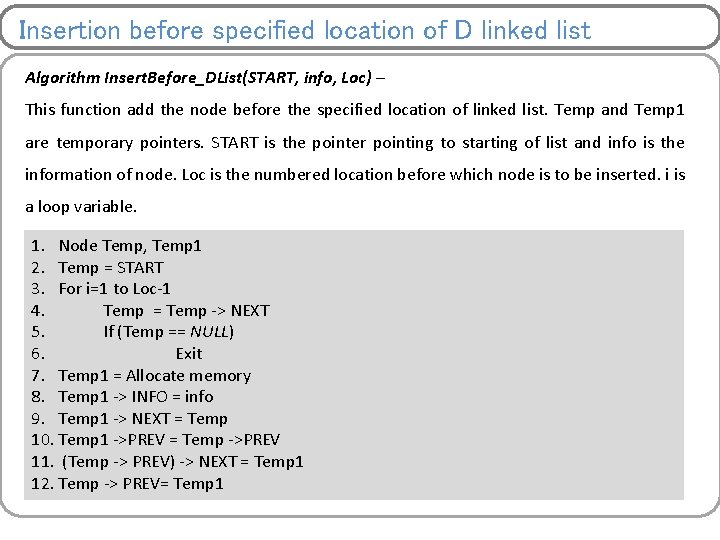
Insertion before specified location of D linked list Algorithm Insert. Before_DList(START, info, Loc) – This function add the node before the specified location of linked list. Temp and Temp 1 are temporary pointers. START is the pointer pointing to starting of list and info is the information of node. Loc is the numbered location before which node is to be inserted. i is a loop variable. 1. Node Temp, Temp 1 2. Temp = START 3. For i=1 to Loc-1 4. Temp = Temp -> NEXT 5. If (Temp == NULL) 6. Exit 7. Temp 1 = Allocate memory 8. Temp 1 -> INFO = info 9. Temp 1 -> NEXT = Temp 10. Temp 1 ->PREV = Temp ->PREV 11. (Temp -> PREV) -> NEXT = Temp 1 12. Temp -> PREV= Temp 1

Insertion at End of Doubly linked list Algorithm Insert. End_DList(END, info) – This function add the node at the end of linked list. Temp and Temp 1 are temporary pointers. END is the pointer pointing to end of list. info is the information of node. 1. 2. 3. 4. 5. 6. 7. 8. Node Temp, Temp 1 Temp = END Temp 1 = Allocate memory Temp 1 -> INFO =info Temp 1 -> NEXT = NULL Temp 1 ->PREV = END Temp ->NEXT = Temp 1 END = Temp 1

Deletion Four ways to Delete a node from linked list – 1. Delete from beginning 2. Delete after specified location 3. Delete before specified location 4. Delete from the end NOTE: Deletion could be done on the base information (to be deleted) available at any node or not. Here, first find that node and then delete it.

Deletion at beginning of linked list Algorithm Delete. Beg_DList(START, END) – This function delete the node at the starting of linked list. Temp is temporary pointer. START and are the pointers pointing to starting of list and end of list. 1. 2. 3. 4. 5. 6. 7. 8. 9. Temp = START If Temp ==NULL Exit If (START == END) START = END =NULL ELSE (Temp ->NEXT) -> PREV =NULL START = Temp -> NEXT Free Temp

Deletion after specified location of linked list Algorithm Delete. After_DList(START, Loc) – This function delete the node after the specified location of linked list. Temp and Temp 1 are temporary pointers. START is the pointer pointing to starting of list and info is the information of node. Loc is the numbered location from where next node is to be deleted. i is a loop variable. 1. Node Temp, Temp 1 2. Temp = START 3. For i=1 to Loc-1 4. Temp = Temp -> NEXT 5. If (Temp == NULL) 6. Exit 7. Temp 1 = Temp ->NEXT 8. Temp -> NEXT = Temp 1 -> NEXT 9. (Temp 1 ->NEXT) ->PREV = Temp 10. Free Temp 1

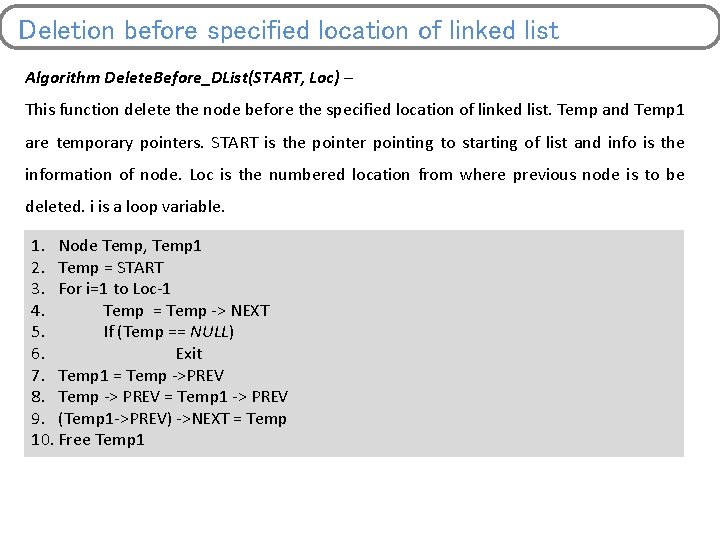
Deletion before specified location of linked list Algorithm Delete. Before_DList(START, Loc) – This function delete the node before the specified location of linked list. Temp and Temp 1 are temporary pointers. START is the pointer pointing to starting of list and info is the information of node. Loc is the numbered location from where previous node is to be deleted. i is a loop variable. 1. Node Temp, Temp 1 2. Temp = START 3. For i=1 to Loc-1 4. Temp = Temp -> NEXT 5. If (Temp == NULL) 6. Exit 7. Temp 1 = Temp ->PREV 8. Temp -> PREV = Temp 1 -> PREV 9. (Temp 1 ->PREV) ->NEXT = Temp 10. Free Temp 1

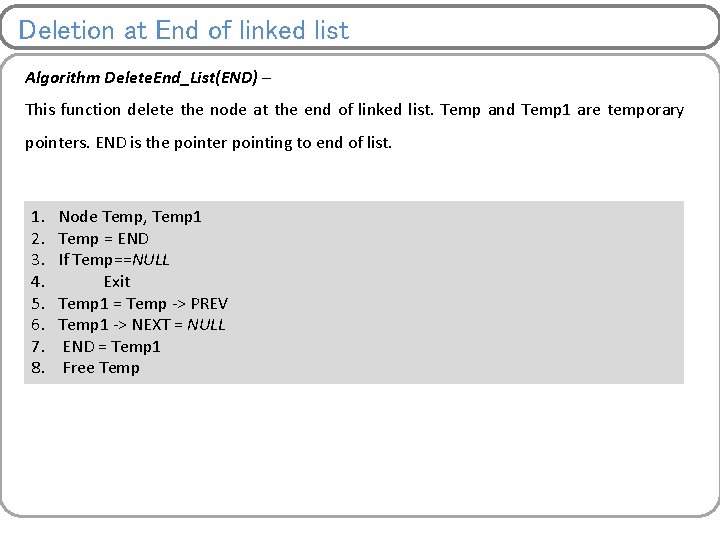
Deletion at End of linked list Algorithm Delete. End_List(END) – This function delete the node at the end of linked list. Temp and Temp 1 are temporary pointers. END is the pointer pointing to end of list. 1. 2. 3. 4. 5. 6. 7. 8. Node Temp, Temp 1 Temp = END If Temp==NULL Exit Temp 1 = Temp -> PREV Temp 1 -> NEXT = NULL END = Temp 1 Free Temp

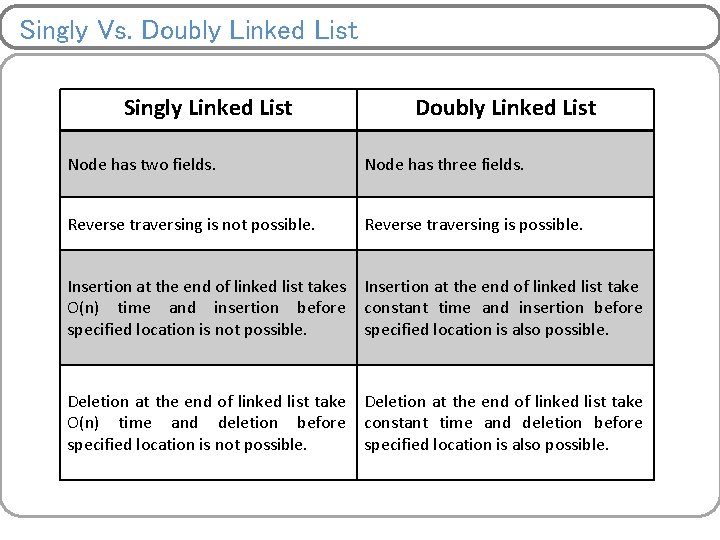
Singly Vs. Doubly Linked List Singly Linked List Doubly Linked List Node has two fields. Node has three fields. Reverse traversing is not possible. Reverse traversing is possible. Insertion at the end of linked list takes Insertion at the end of linked list take O(n) time and insertion before constant time and insertion before specified location is not possible. specified location is also possible. Deletion at the end of linked list take O(n) time and deletion before constant time and deletion before specified location is not possible. specified location is also possible.

Exercises 1. Write an algorithm for searching in doubly linked list. 2. Write an algorithm for sorting in singly linked list. 3. Why reverse algorithm is not needed in doubly linked list. Justify your answer comparing with singly linked list. 4. Write an algorithm to delete the entire singly linked list or doubly linked list.

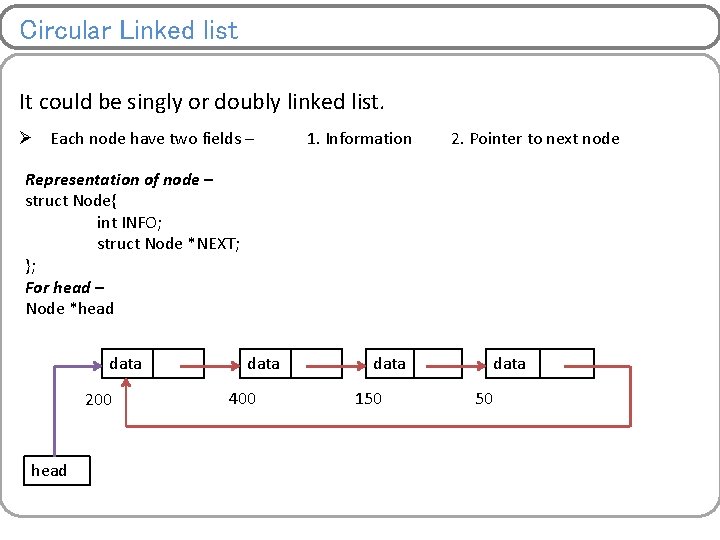
Circular Linked list It could be singly or doubly linked list. Ø Each node have two fields – 1. Information 2. Pointer to next node Representation of node – struct Node{ int INFO; struct Node *NEXT; }; For head – Node *head data 200 head data 400 data 150 data 50

Supported operations Ø All operation which can be performed on singly or doubly linked list can be extended to circular by maintaining last node next pointer to first node. 1. Creating empty linked list 2. Appending nodes to linked list 3. Traversing 4. Insertion 5. Deletion 6. Searching 7. Sorting How do we know end of list ? Compare next pointer field with address of first node or head

Circular Linked list Advantages: Ø We can go to any node, in linear linked list it is not possible to go to previous node. Ø It saves time when we have to go to the first node from the last node. It can be done in single step because there is no need to traverse the in between nodes. But in double linked list, we will have to go through in between nodes. Disadvantages: 1. It is not easy to reverse the linked list. If proper care is not taken, then the problem of infinite loop can occur. 2. If we want to go back to the previous node, then we can not do it in single step. Entire circle to be covered.

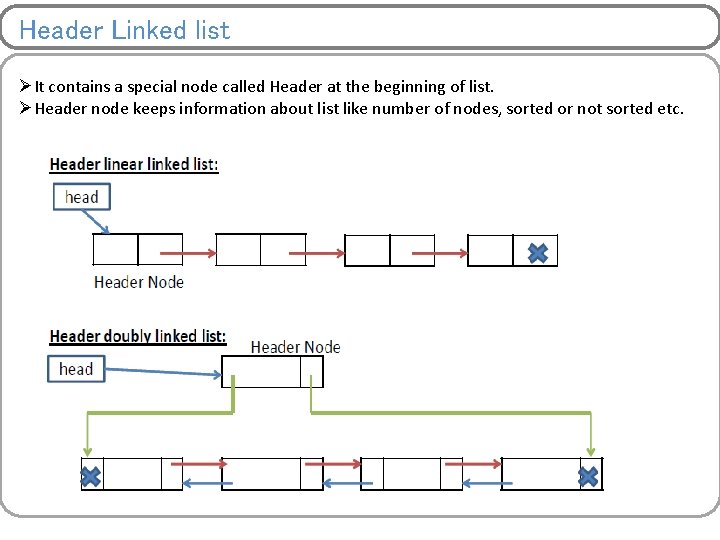
Header Linked list ØIt contains a special node called Header at the beginning of list. ØHeader node keeps information about list like number of nodes, sorted or not sorted etc.

Application of Linked list ØTo maintain directory ØTo represent sparse matrices ØTo implement other data structures like stack, queue, tree etc. ØTo manipulate polynomials

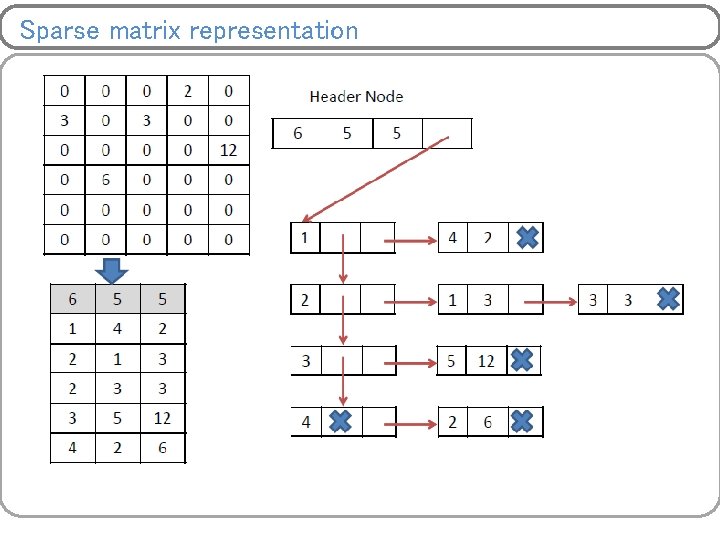
Sparse matrix representation

Polynomial representation

Polynomial Addition Algorithm Add_Poly(poly 1, poly 2, poly 3) – This algorithm adds two given polynomial poly 1 and poly 2 and resultant polynomial is poly 3. This algorithms calls append_node algorithm which is being used to add the resultant node into poly 3.

Polynomial representation 1. While (poly 1!=NULL and poly 2!=NULL) 2. If (poly 1 ->pow > poly 2 ->pow) 3. coeff = poly 1 ->coef 4. powe = poly 1 ->pow 5. poly 1 = poly 1 -> NEXT 6. Else If (poly 1 ->pow < poly 2 ->pow) 7. coeff = poly 2 ->coef 8. powe = poly 2 ->pow 9. poly 2 = poly 2 -> NEXT 10. Else 11. coeff = poly 1 ->coef + poly 2 ->coef 12. powe = poly 1 ->pow 13. poly 1 = poly 1 ->NEXT 14. poly 2 = poly 2 ->NEXT 15. If (coeff !=0) 16. append_node(poly 3, coef, powe) 17. If(poly 1 == NULL) 18. While (poly 2!=NULL) 19. append_node(poly 3, poly 2 ->coef, poly 2 ->pow) 20. poly 2 = poly 2 ->NEXT 21. If(poly 2 == NULL) 22. While (poly 1!=NULL) 23. append_node(poly 3, poly 1 ->coef, poly 1 ->pow) 24. poly 1 = poly 1 ->NEXT

Polynomial Addition Algorithm append_node is same as Append_List. But here we have three fields instead of two fields. Exercise – Write an algorithm for appending polynomial node into list.