Polynomial Addition using Linked lists Data Structures Polynomial

Polynomial Addition using Linked lists Data Structures

Polynomial ADT A single variable polynomial can be generalized as: An example of a single variable polynomial: 4 x 6 + 10 x 4 - 5 x + 3 Remark: the order of this polynomial is 6 (look for highest exponent)

• Polynomial ADT (continued) • By definition of a data types: A set of values and a set of allowable operations on those values. We can now operate on this polynomial the way we like…

• Polynomial ADT • What kinds of operations? Here are the most common operations on a polynomial: • Add & Subtract • Multiply • Differentiate • Integrate • etc…

• Polynomial ADT • What kinds of operations? Here are the most common operations on a polynomial: • Add & Subtract • Multiply • Differentiate • Integrate • etc…

• Polynomial ADT (continued) • Why implement this? Calculating polynomial operations by hand can be very cumbersome. Take differentiation as an example: d(23 x 9 + 18 x 7 + 41 x 6 + 163 x 4 + 5 x + 3)/dx = (23*9)x(9 -1) + (18*7)x(7 -1) + (41*6)x(6 -1) + …

• Polynomial ADT (continued) • How to implement this? There are different ways of implementing the polynomial ADT: • Array (not recommended) • Linked List (preferred and recommended)

• Polynomial ADT (continued) • Array Implementation: • p 1(x) = 8 x 3 + 3 x 2 + 2 x + 6 • p 2(x) = 23 x 4 + 18 x - 3 p 1(x) 6 0 2 p 2(x) 3 8 -3 0 2 Index represents exponents 18 0 23 4

• Polynomial ADT (continued) • This is why arrays aren’t good to represent polynomials: • p 3(x) = 16 x 21 - 3 x 5 + 2 x + 6 6 2 0 0 -3 0 ………… WASTE OF SPACE! 0 16

• Polynomial ADT (continued) • Advantages of using an Array: • only good for non-sparse polynomials. • ease of storage and retrieval. • Disadvantages of using an Array: • have to allocate array size ahead of time. • huge array size required for sparse polynomials. Waste of space and runtime.

• Polynomial ADT (continued) • Linked list Implementation: • p 1(x) = 23 x 9 + 18 x 7 + 41 x 6 + 163 x 4 + 3 • p 2(x) = 4 x 6 + 10 x 4 + 12 x + 8 P 1 23 9 18 7 41 6 18 7 8 0 TAIL (contains pointer) P 2 4 6 10 4 12 1 NODE (contains coefficient & exponent) 3 0

• Polynomial ADT (continued) • Advantages of using a Linked list: • save space (don’t have to worry about sparse polynomials) and easy to maintain • don’t need to allocate list size and can declare nodes (terms) only as needed • Disadvantages of using a Linked list : • can’t go backwards through the list • can’t jump to the beginning of the list from the end.

• Polynomial ADT (continued) • Adding polynomials using a Linked list representation: (storing the result in p 3) To do this, we have to break the process down to cases: • Case 1: exponent of p 1 > exponent of p 2 • Copy node of p 1 to end of p 3. [go to next node] • Case 2: exponent of p 1 < exponent of p 2 • Copy node of p 2 to end of p 3. [go to next node]

• Polynomial ADT (continued) • Case 3: exponent of p 1 = exponent of p 2 • Create a new node in p 3 with the same exponent and with the sum of the coefficients of p 1 and p 2.

Polynomials Representation struct polynode { int coef; int exp; struct polynode * next; }; typedef struct polynode *polyptr; coef exp next

Example a b 3 14 2 8 14 -3 10 8 1 0 null 10 6 null

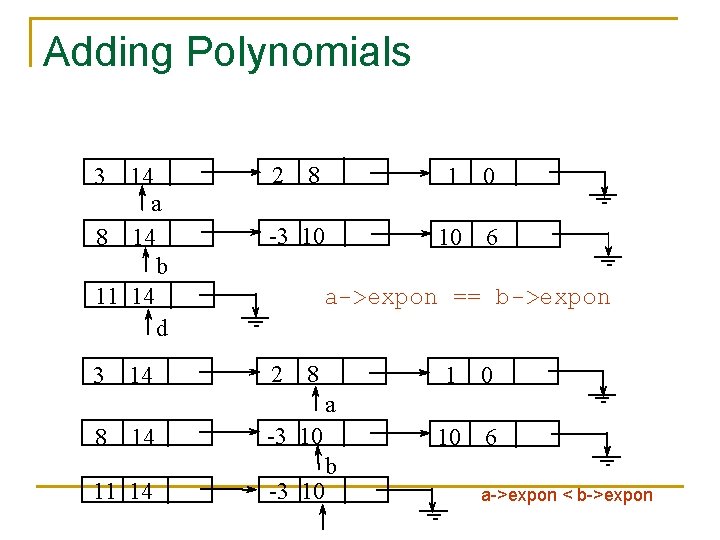
Adding Polynomials 3 14 a 8 14 b 11 14 d 3 14 2 8 1 0 -3 10 10 6 a->expon == b->expon 2 8 1 0 10 6 a 8 14 11 14 -3 10 b -3 10 a->expon < b->expon

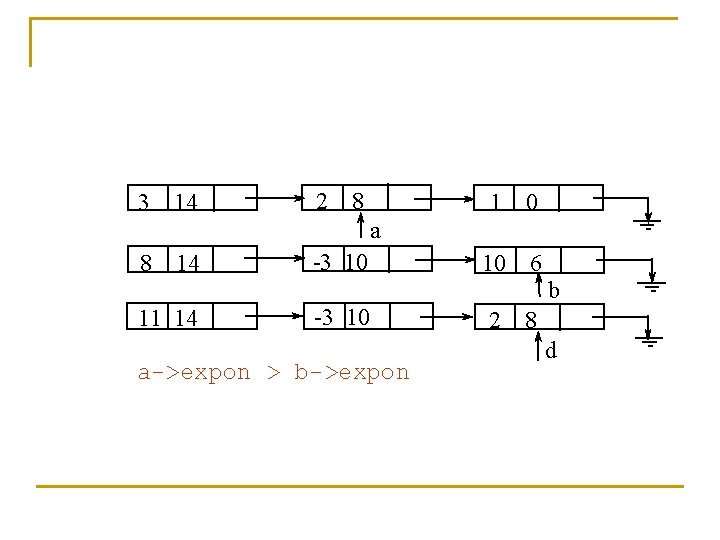
3 14 2 8 1 0 10 6 a 8 14 -3 10 b 11 14 -3 10 a->expon > b->expon 2 8 d

C Program to implement polynomial Addition struct polynode { int coef; int exp; struct polynode *next; }; typedef struct polynode *polyptr;

polyptr create. Poly() { polyptr p, tmp, start=NULL; int ch=1; while(ch) { p=(polyptr)malloc(sizeof(struct polynode)); printf("Enter the coefficient : "); scanf("%d", &p->coef); printf("Enter the exponent : "); scanf("%d", &p->exp); p->next=NULL; //IF the polynomial is empty then add this node as the start node of the polynomial if(start==NULL) start=p; //else add this node as the last term in the polynomial lsit else { tmp=start; while(tmp->next!=NULL) tmp=tmp->next; tmp->next=p; }

printf("MORE Nodes to be added (1/0): "); scanf("%d", &ch); } return start; } start 3 14 2 8 1 0 null

void display(polyptr *poly) {polyptr list; list=*poly; while(list!=NULL) { if(list->next!=NULL) printf("%d X^ %d + " , list->coef, list->exp); else printf("%d X^ %d " , list->coef, list->exp); list=list->next; } }

polyptr add. Two. Polynomial(polyptr *F, polyptr *S) { polyptr A, B, p, result, C=NULL; A=*F; B=*S; result=C; while(A!=NULL && B!=NULL) { switch(compare(A->exp, B->exp)) { case 1: p=(polyptr)malloc(sizeof(struct polynode)); p->coef=A->coef; p->exp=A->exp; p->next=NULL; A=A->next; if (result==NULL) result=p; else attach. Term(p->coef, p->exp, &result); break;

case 0: p=(polyptr)malloc(sizeof(struct polynode)); p->coef=A->coef+B->coef; p->exp=A->exp; p->next=NULL; A=A->next; B=B->next; if (result==NULL) result=p; else attach. Term(p->coef, p->exp, &result); break;

case -1: p=(polyptr)malloc(sizeof(struct polynode)); p->coef=B->coef; p->exp=B->exp; p->next=NULL; B=B->next; if (result==NULL) result=p; else attach. Term(p->coef, p->exp, &result); break; }// End of Switch }// end of while

while(A!=NULL) { attach. Term(A->coef, A->exp, &result); A=A->next; } while(B!=NULL) { attach. Term(B->coef, B->exp, &result); B=B->next; } return result; }//end of addtwopolynomial function

int compare(int x, int y) { if(x==y) return 0; if(x<y)return -1; if(x>y) return 1; }

Contd. . attach. Term(int c, int e, polyptr *p) { polyptr ptr, tmp; ptr=*p; tmp=(polyptr)malloc(sizeof(struct polynode)); while(ptr->next!=NULL) { ptr=ptr->next; } ptr->next=tmp; tmp->coef=c; tmp->exp=e; tmp->next=NULL; }

main() { polyptr Apoly, Bpoly; clrscr(); printf("Enter the first polynomial : n"); Apoly=create. Poly(); display(&Apoly); printf("n"); Bpoly=create. Poly(); display(&Bpoly); printf("n. Result is : "); C=add. Two. Polynomial(&Apoly, &Bpoly); display(&C); getch(); }

Exercise n Write a program to implement polynomial multiplication.