Linked Lists Definition of Linked Lists Examples of

Linked Lists • • • Definition of Linked Lists Examples of Linked Lists Operations on Linked Lists Linked List as a Class Linked Lists as Implementations of Stacks, Sets, etc. CS 103 1

Definition of Linked Lists • A linked list is a sequence of items (objects) where every item is linked to the next. • Graphically: data tail_ptr head_ptr CS 103 2

Definition Details • Each item has a data part (one or more data members), and a link that points to the next item • One natural way to implement the link is as a pointer; that is, the link is the address of the next item in the list • It makes good sense to view each item as an object, that is, as an instance of a class. • We call that class: Node • The last item does not point to anything. We set its link member to NULL. This is denoted graphically by a self-loop CS 103 3

Examples of Linked Lists (A Waiting Line) • A waiting line of customers: John, Mary, Dan, Sue (from the head to the tail of the line) • A linked list of strings can represent this line: John Mary Dan Sue tail_ptr head_ptr CS 103 4

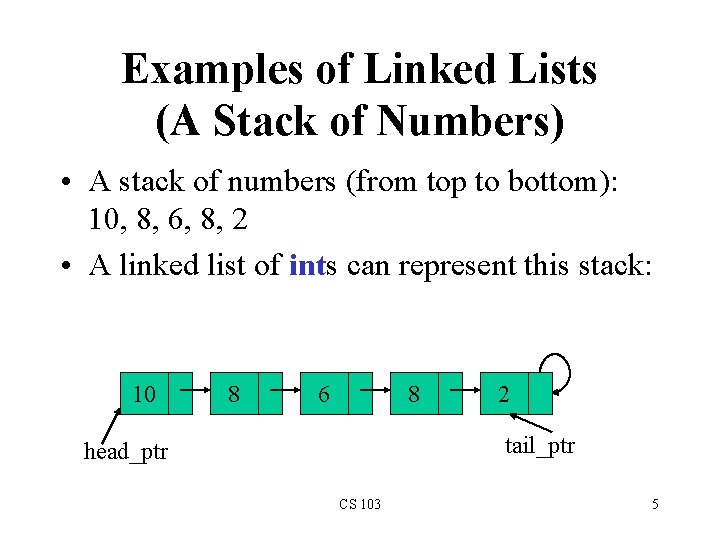
Examples of Linked Lists (A Stack of Numbers) • A stack of numbers (from top to bottom): 10, 8, 6, 8, 2 • A linked list of ints can represent this stack: 10 8 6 8 2 tail_ptr head_ptr CS 103 5

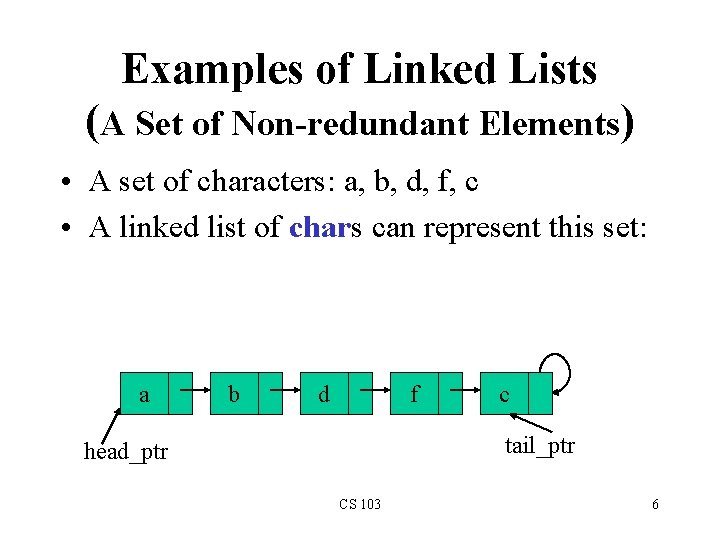
Examples of Linked Lists (A Set of Non-redundant Elements) • A set of characters: a, b, d, f, c • A linked list of chars can represent this set: a b d f c tail_ptr head_ptr CS 103 6

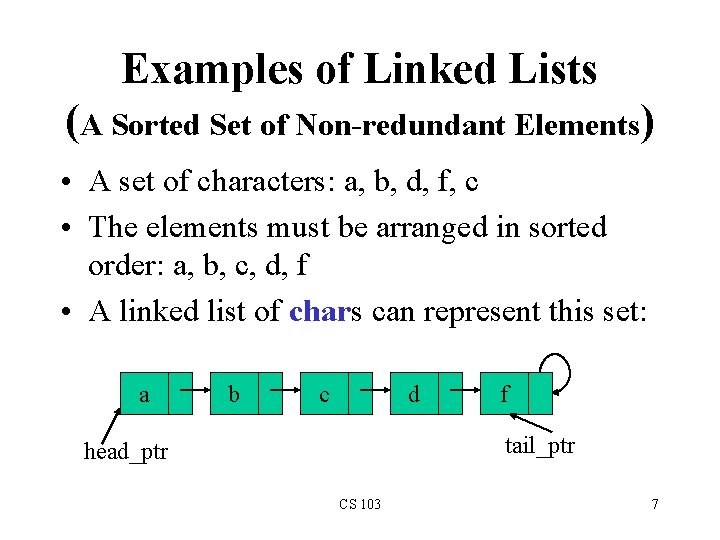
Examples of Linked Lists (A Sorted Set of Non-redundant Elements) • A set of characters: a, b, d, f, c • The elements must be arranged in sorted order: a, b, c, d, f • A linked list of chars can represent this set: a b c d f tail_ptr head_ptr CS 103 7

Examples of Linked Lists (A Polynomial) • A polynomial of degree n is the function Pn(x)=a 0+a 1 x+a 2 x 2+…+anxn. The ai’s are called the coefficients of the polynomial • The polynomial can be represented by a linked list (2 data members and a link per item): a 0, 0 a 1, 1 a 2, 2 an, n tail_ptr head_ptr CS 103 8

Operations on Linked Lists • Insert a new item – At the head of the list, or – At the tail of the list, or – Inside the list, in some designated position • Search for an item in the list – The item can be specified by position, or by some value • Delete an item from the list – Search for and locate the item, then remove the item, and finally adjust the surrounding pointers • size( ); • is. Empty( ) CS 103 9

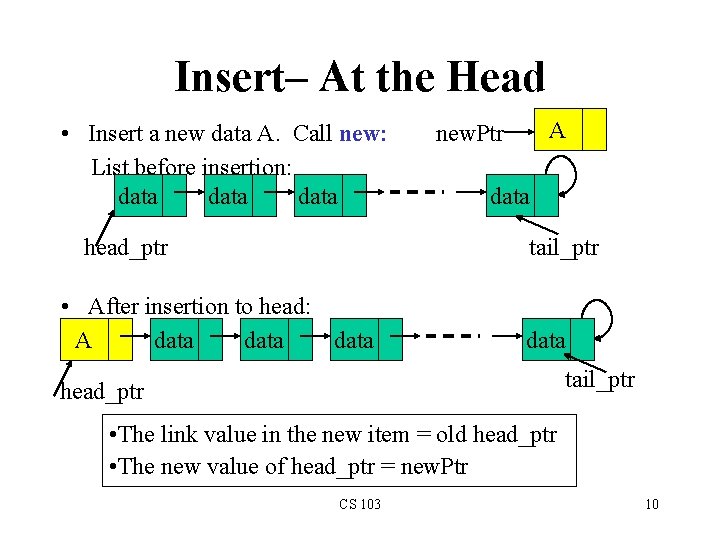
Insert– At the Head • Insert a new data A. Call new: List before insertion: data head_ptr A new. Ptr data tail_ptr • After insertion to head: A data tail_ptr head_ptr • The link value in the new item = old head_ptr • The new value of head_ptr = new. Ptr CS 103 10

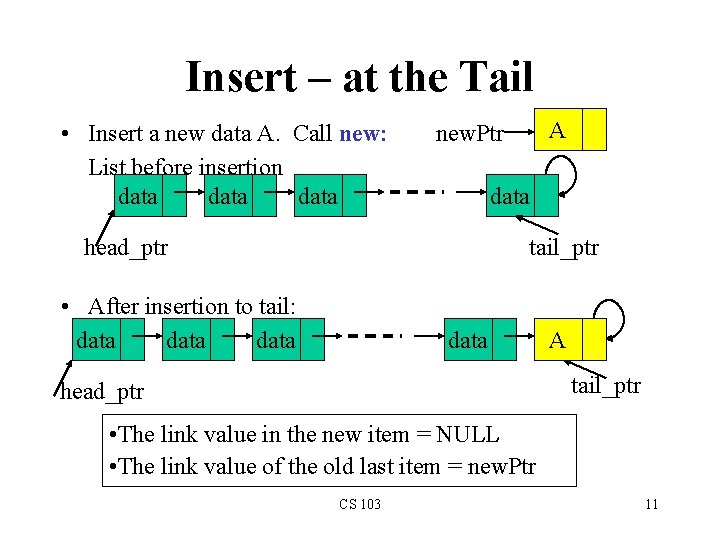
Insert – at the Tail • Insert a new data A. Call new: List before insertion data A new. Ptr data head_ptr tail_ptr • After insertion to tail: data A tail_ptr head_ptr • The link value in the new item = NULL • The link value of the old last item = new. Ptr CS 103 11

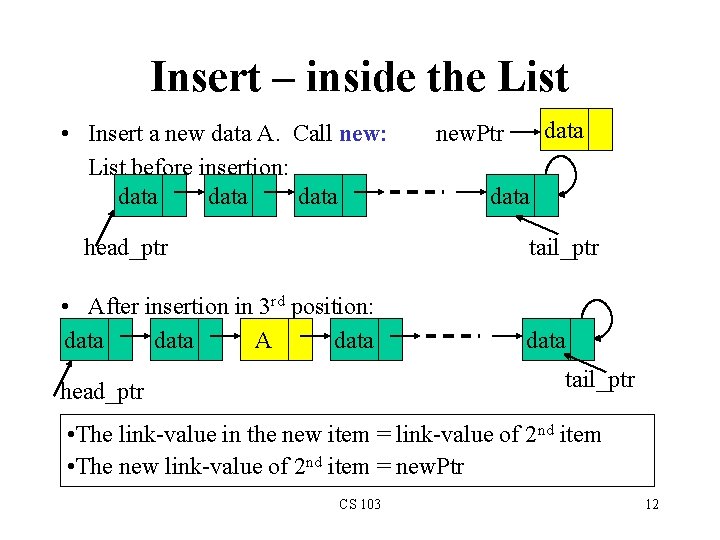
Insert – inside the List • Insert a new data A. Call new: List before insertion: data head_ptr data new. Ptr data tail_ptr • After insertion in 3 rd position: data A data tail_ptr head_ptr • The link-value in the new item = link-value of 2 nd item • The new link-value of 2 nd item = new. Ptr CS 103 12

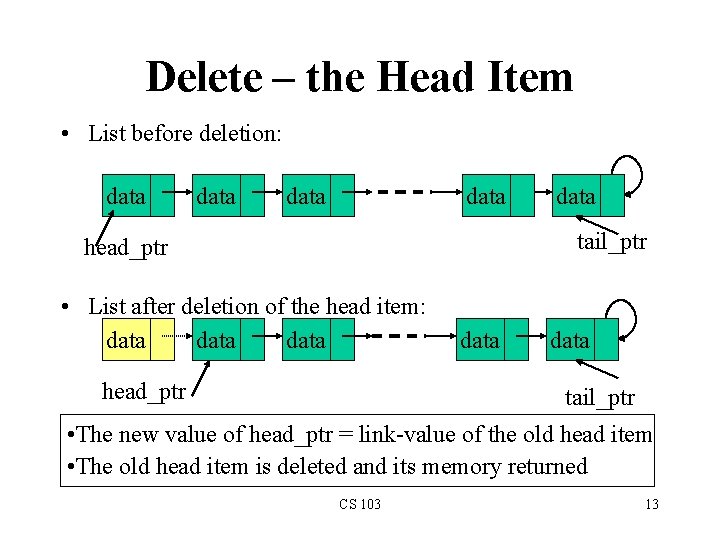
Delete – the Head Item • List before deletion: data data tail_ptr head_ptr • List after deletion of the head item: data head_ptr data tail_ptr • The new value of head_ptr = link-value of the old head item • The old head item is deleted and its memory returned CS 103 13

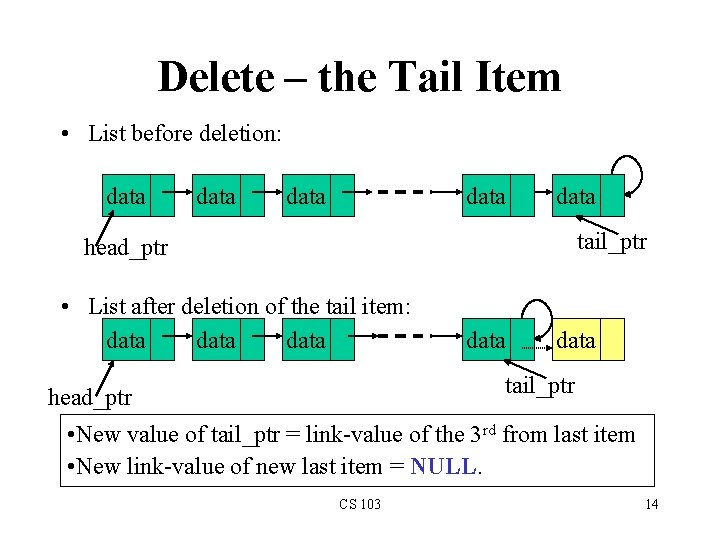
Delete – the Tail Item • List before deletion: data data tail_ptr head_ptr • List after deletion of the tail item: data data tail_ptr head_ptr • New value of tail_ptr = link-value of the 3 rd from last item • New link-value of new last item = NULL. CS 103 14

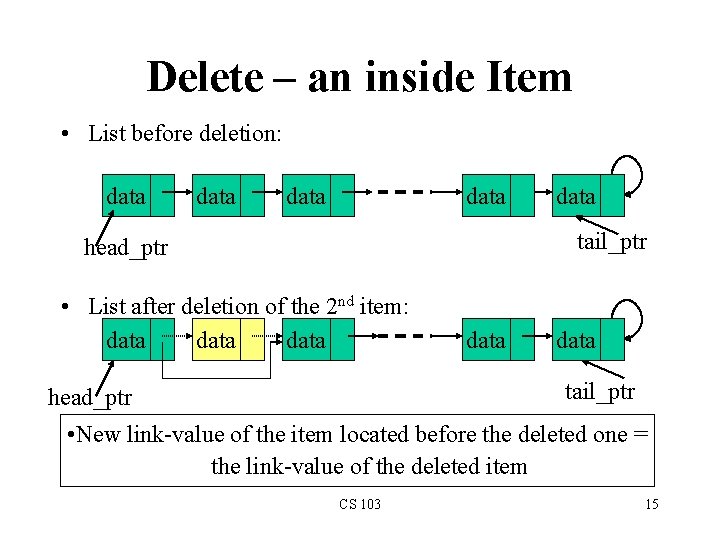
Delete – an inside Item • List before deletion: data data tail_ptr head_ptr • List after deletion of the 2 nd item: data data tail_ptr head_ptr • New link-value of the item located before the deleted one = the link-value of the deleted item CS 103 15

size() and is. Empty() • We need to scan the items in the list from the head_ptr to the last item marked by its link-value being NULL • Count the number of items in the scan, and return the count. This is the size(). • Alternatively, keep a counter of the number of item, which gets updated after each insert/delete. The function size( ) returns that counter • If head_ptr is NULL, is. Empty() returns true; else, it returns false. CS 103 16

Searching for an Item • Suppose you want to find the item whose data value is A • You have to search sequentially starting from the head item rightward until the first item whose data member is equal to A is found. • At each item searched, a comparison between the data member and A is performed. CS 103 17

Time of the Operations • Time to search() is O(L) where L is the relative location of the desired item in the List. In the worst case. The time is O(n). In the average case it is O(N/2)=O(n). • Time for remove() is dominated by the time for search, and is thus O(n). • Time for insert at head or at tail is O(1). • Time for insert at other positions is dominated by search time, and thus O(n). • Time for size() is O(1), and time for is. Empty() is O(1) CS 103 18

Implementation of an Item • Each item is a collection of data and pointer fields, and should be able to support some basic operations such as changing its link value and returning its member data • Therefore, a good implementation of an item is a class • The class will be called Node CS 103 19

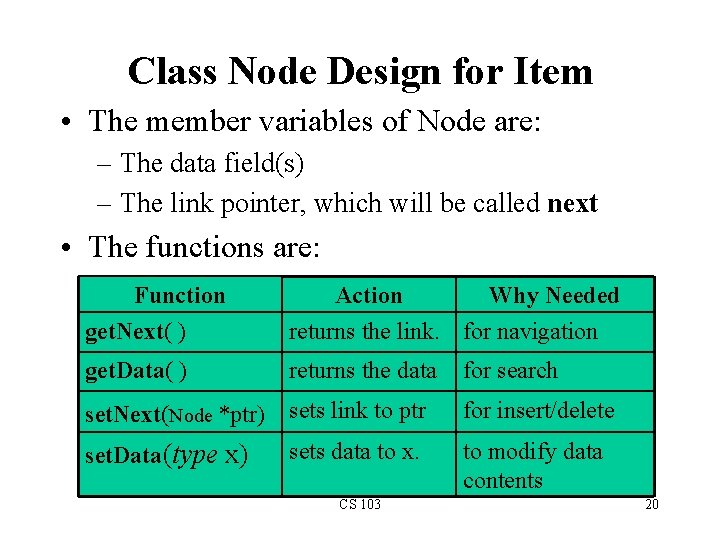
Class Node Design for Item • The member variables of Node are: – The data field(s) – The link pointer, which will be called next • The functions are: Function get. Next( ) Action Why Needed returns the link. for navigation get. Data( ) returns the data for search set. Next(Node *ptr) sets link to ptr for insert/delete set. Data(type x) sets data to x. to modify data contents CS 103 20

Class Node Type • class Node { private: int data; // different data type for other apps Node *next; // the link pointer to next item public: Node(int x=0; Node * ptr=NULL); // constructor int get. Data( ); Node *get. Next( ); void set. Data(int x); void set. Next(Node *ptr); }; CS 103 21

Class Node Implementation • • • Node: : Node(int x, Node *p){ data=x; next=p; }; int Node: : get. Data( ){return data; }; Node * Node: : get. Next( ){return next; }; void Node: : set. Data(int x) {data=x; }; void Node: : set. Next(Node *ptr){next=ptr; }; CS 103 22

Implementation of Linked List • A linked list is a collection of Node objects, and must support a number of operations • Therefore, it is sensible to implement a linked list as a class • The class name for it is List CS 103 23

Class Design for List • The member variables are: – Node *head_ptr; Node *tail_ptr; – int num. Of. Items; • Member functions – Node * search(int x); Node * item. At(int position); – void remove. Head(); void remove. Tail(); void remove(int x); – void insert. Head(int x); void insert. Tail(int x); void insert(Node *p, int x) // inserts item after the item // pointed to by p – int size( ); Node *get. Head( ); Node get. Tail( ); – bool is. Empty( ); CS 103 24

Class List Type • class List { private: Node *head_ptr; Node *tail_ptr; int num. Of. Items; public: List( ); // constructor int size( ); Node *get. Head( ); Node *get. Tail( ); bool is. Empty( ); Node *search(int x); Node *item. At(int position); void remove. Head(); void remove. Tail(); void remove(int x); // delete leftmost item having x void insert. Head(int x); void insert. Tail(int x); void insert(Node *p, int x); }; CS 103 25

Implementation of Class List • List: : List( ){head_ptr= NULL; tail_ptr=NULL; num. Of. Items=0; }; • int List: : size( ){return num. Of. Items; }; • Node * List: : get. Head( ) {return head_ptr; }; • Node * List: : get. Tail( ) {return tail_ptr; }; • bool List: : is. Empty() {return (num. Of. Item==0); }; CS 103 26

Implementation of search( ) • Node *List: : search(int x){ Node * current. Ptr = get. Head( ); while (current. Ptr != NULL){ if (current. Ptr->get. Data( ) == x) return current. Ptr; else current. Ptr = current. Ptr->get. Next(); } return NULL; // Now x is not, so return NULL }; CS 103 27

Implementation of item. At( ) • Node *List: : item. At(int position){ if (position<0 || position>=num. Of. Items) return NULL; Node * current. Ptr = get. Head( ); for(int k=0; k != position; k++) current. Ptr = current. Ptr -> get. Next( ); return current. Ptr; }; CS 103 28

Implementation of remove. Head( ) • void List: : remove. Head( ){ if (num. Of. Items == 0) return; Node * current. Ptr = get. Head( ); head_ptr=head_ptr->get. Next( ); delete current. Ptr; num. Of. Items--; }; CS 103 29

Implementation of remove. Tail( ) • void List: : remove. Tail( ){ if (num. Of. Items == 0) return; if (head_ptr == tail_ptr){ head_ptr=NULL; tail_ptr= NULL; num. Of. Items=0; return; } Node * before. Last = item. At(num. Of. Items-2); before. Last->set. Next(NULL); // before. Last becomes last delete tail_ptr; // deletes the last object tail_ptr=before. Last; num. Of. Items--; }; CS 103 30

Implementation of remove( ) • void List: : remove(int x){ if (num. Of. Items == 0) return; if (head_ptr==tail_ptr && head_ptr->get. Data()==x){ head_ptr=NULL; tail_ptr= NULL; num. Of. Items=0; return; } Node * before. Ptr=head_ptr; // before. Ptr trails current. Ptr Node * current. Ptr=head_ptr->get. Next(); Node * tail = get. Tail(); while (current. Ptr != tail) if (current. Ptr->get. Data( ) == x){ // x is found. Do the bypass before. Ptr->set. Next(current. Ptr->get. Next()); delete current. Ptr; num. Of. Items--; } else { // x is not found yet. Forward before. Ptr & current. Ptr. before. Ptr = current. Ptr; current. Ptr = current. Ptr->get. Next(); } }; CS 103 31

Implementation of insert. Head( ) • void List: : insert. Head(int x){ Node * new. Head = new Node(x, head_ptr); head_ptr= new. Head; if (tail_ptr == NULL) // only one item in list tail_ptr = head_ptr; num. Of. Items++; }; CS 103 32

Implementation of insert. Tail( ) • void List: : insert. Tail(int x){ if (is. Empty()) insert. Head(x); else{ Node * new. Tail = new Node(x); tail_ptr->set. Next(new. Tail); tail_ptr = new. Tail; num. Of. Items++; } }; CS 103 33

Implementation of insert( ) • // inserts item x after the item pointed to by p • void List: : insert(Node *p, int x){ Node *current. Ptr = head_ptr; while(current. Ptr !=NULL && current. Ptr != p) current. Ptr = current. Ptr->get. Next(); if (current. Ptr != NULL ) { // p is found Node *new. Nd=new Node(x, p->get. Next()); p->set. Next(new. Nd); num. Of. Items++; } }; CS 103 34

For your Work in the Lab • Make the necessary modifications to the List class implementations so that no two Nodes have the same data value. This is useful when using linked lists to implement sets. • Make the necessary changes to the List class so that the Nodes are in increasing order of data values. In particular, replace all the insert methods, and replace them with insert(int x), which inserts x in the right position so that the List remains sorted. CS 103 35