Data Structures Algorithms Lecture 3 Data Structures Algorithms

Data Structures & Algorithms Lecture # 3

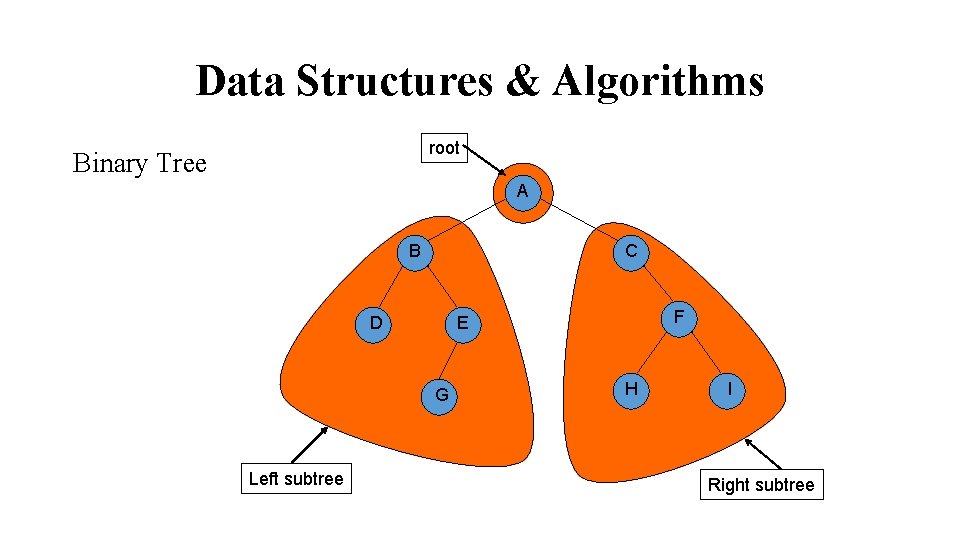
Data Structures & Algorithms Binary Tree: A binary tree is a finite set of elements that is either empty or is partitioned into three disjoint subsets. The first subset contains a single element called the root of the tree. The other two subsets are themselves binary trees called the left and right subtrees. Each element of a binary tree is called a node of the tree.

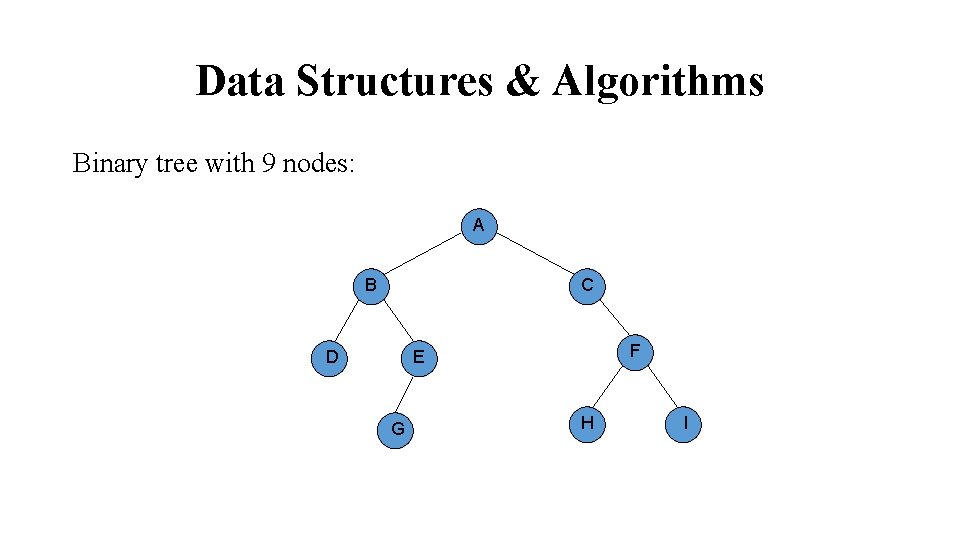
Data Structures & Algorithms Binary tree with 9 nodes: A B C F E D G H I

Data Structures & Algorithms root Binary Tree A B C G Left subtree F E D H I Right subtree

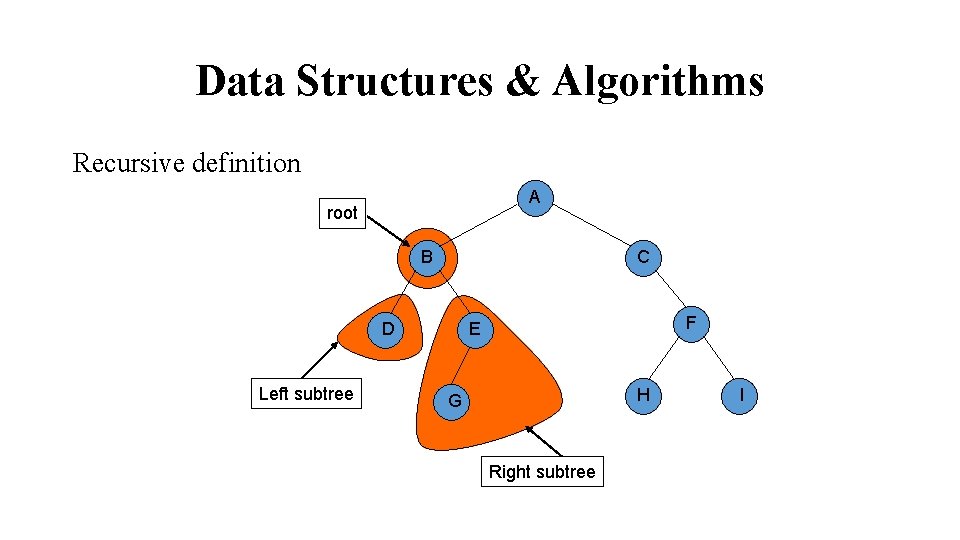
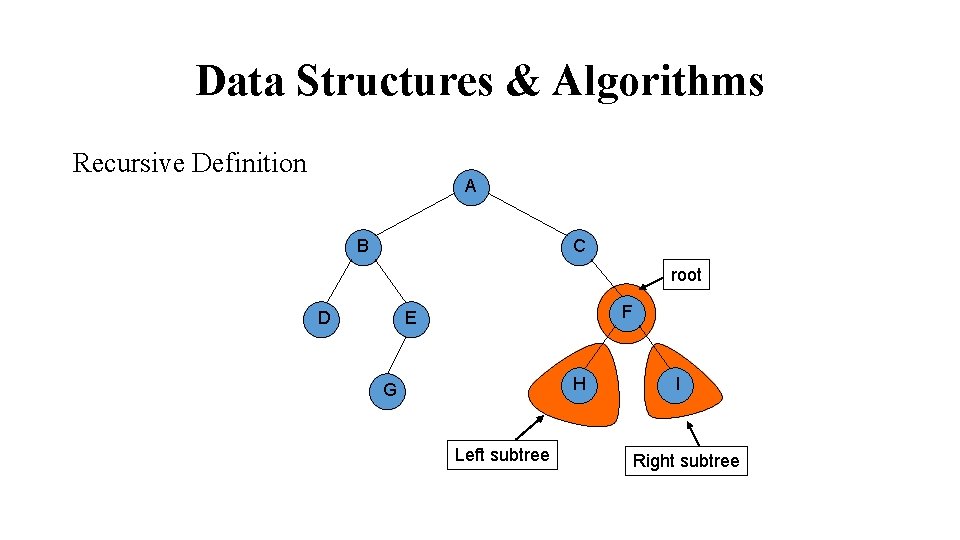
Data Structures & Algorithms Recursive definition A root B C Left subtree F E D H G Right subtree I

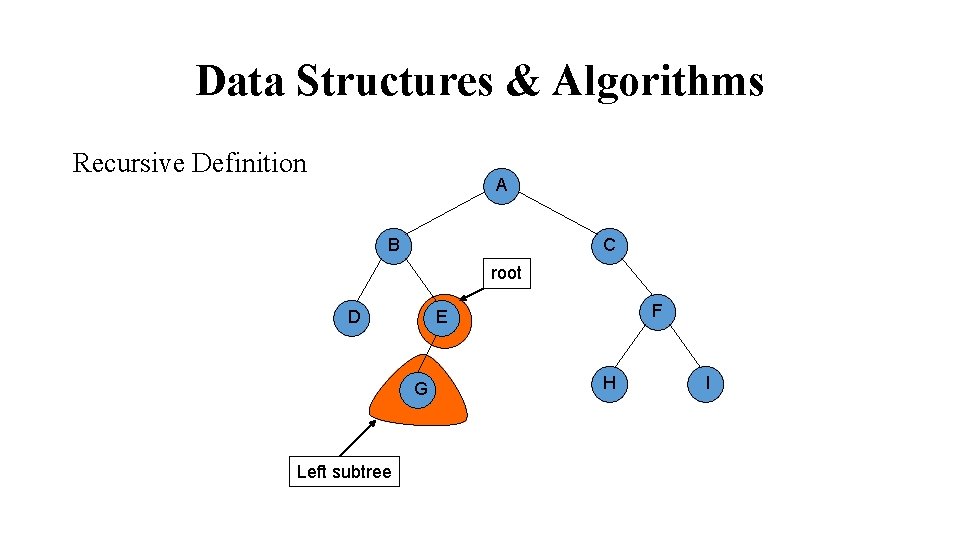
Data Structures & Algorithms Recursive Definition A B C root G Left subtree F E D H I

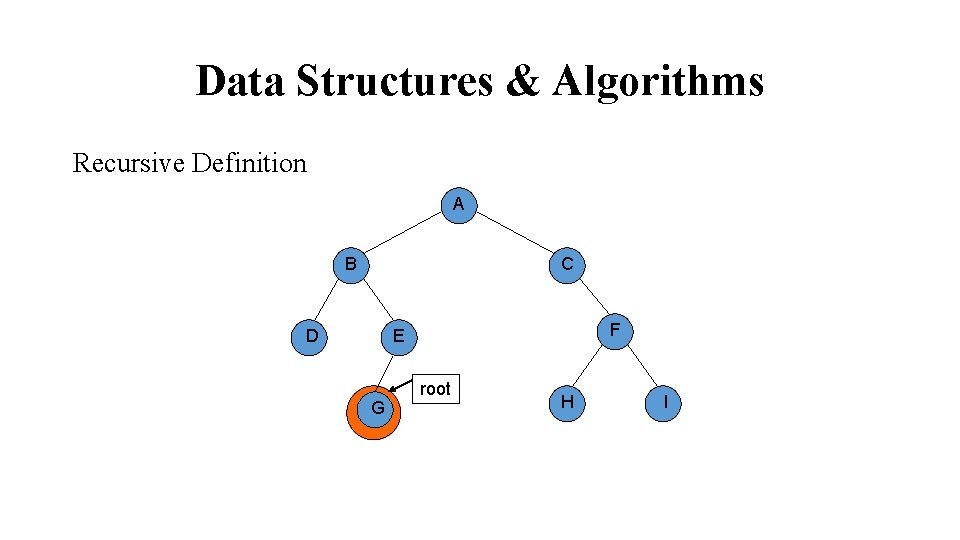
Data Structures & Algorithms Recursive Definition A B C F E D G root H I

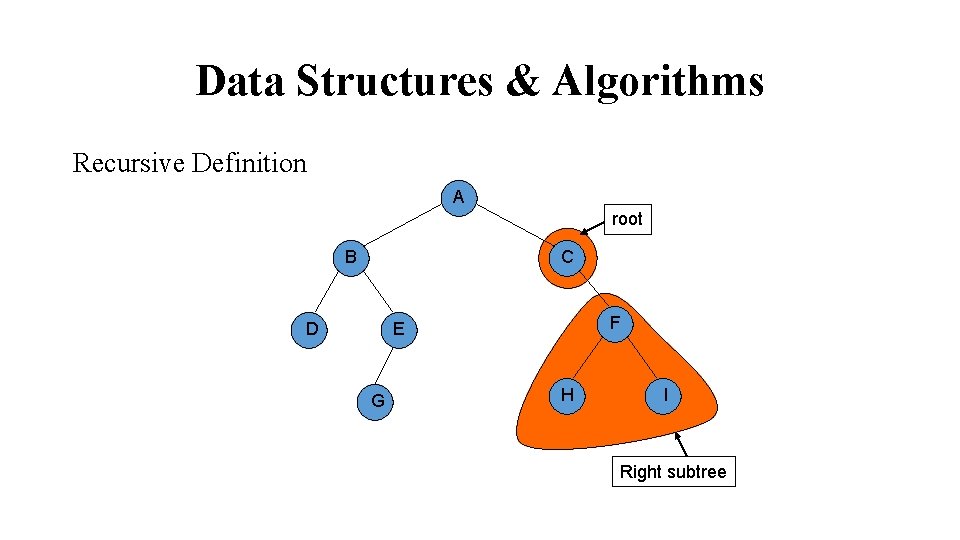
Data Structures & Algorithms Recursive Definition A root B C F E D G H I Right subtree

Data Structures & Algorithms Recursive Definition A B C root F E D H G Left subtree I Right subtree

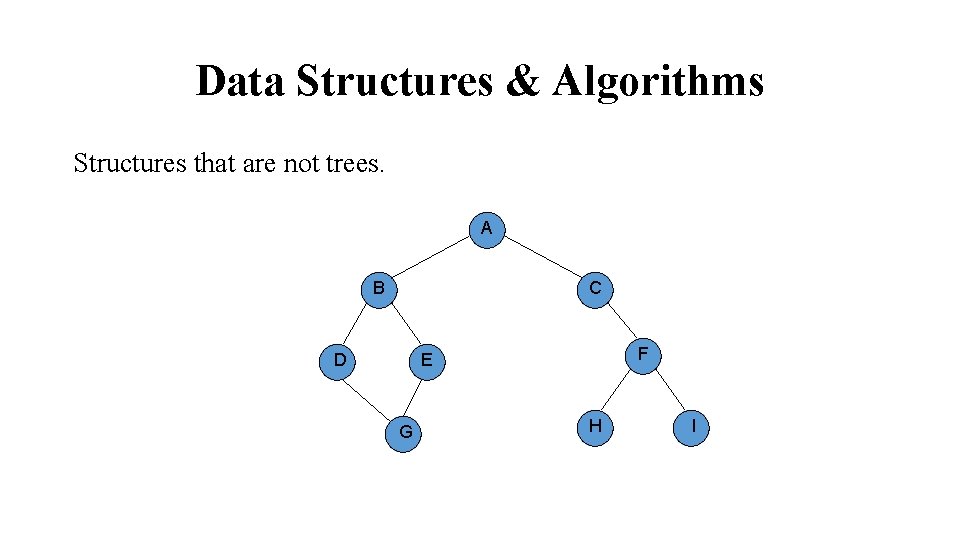
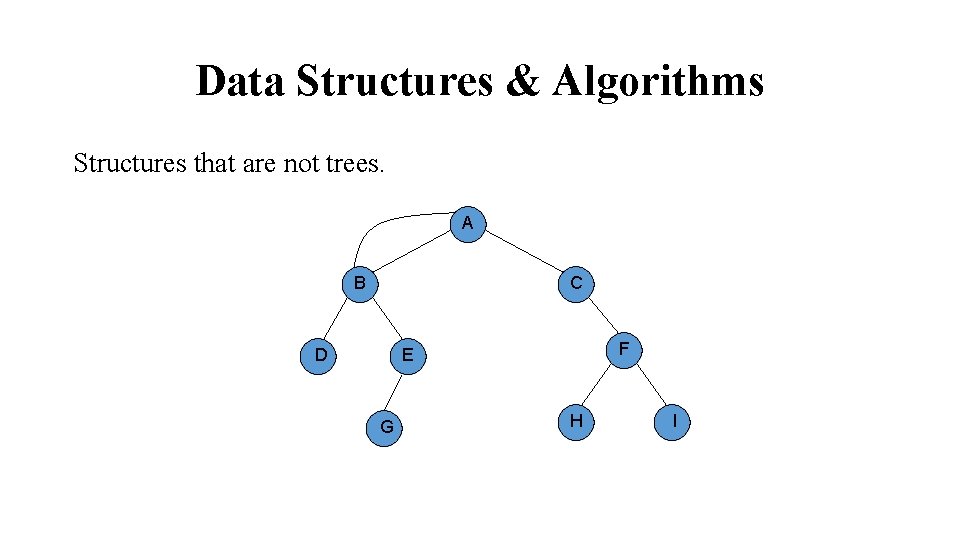
Data Structures & Algorithms Structures that are not trees. A B C F E D G H I

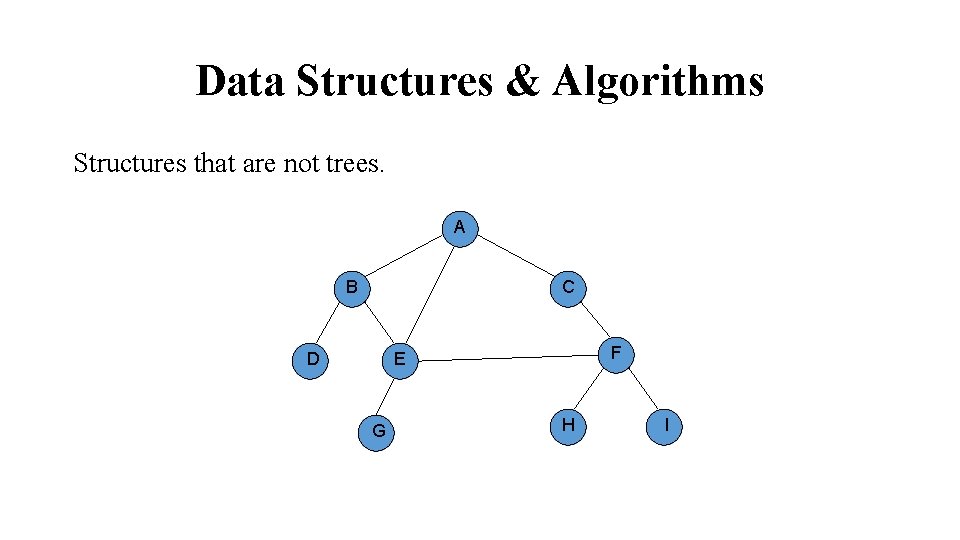
Data Structures & Algorithms Structures that are not trees. A B C F E D G H I

Data Structures & Algorithms Structures that are not trees. A B C F E D G H I

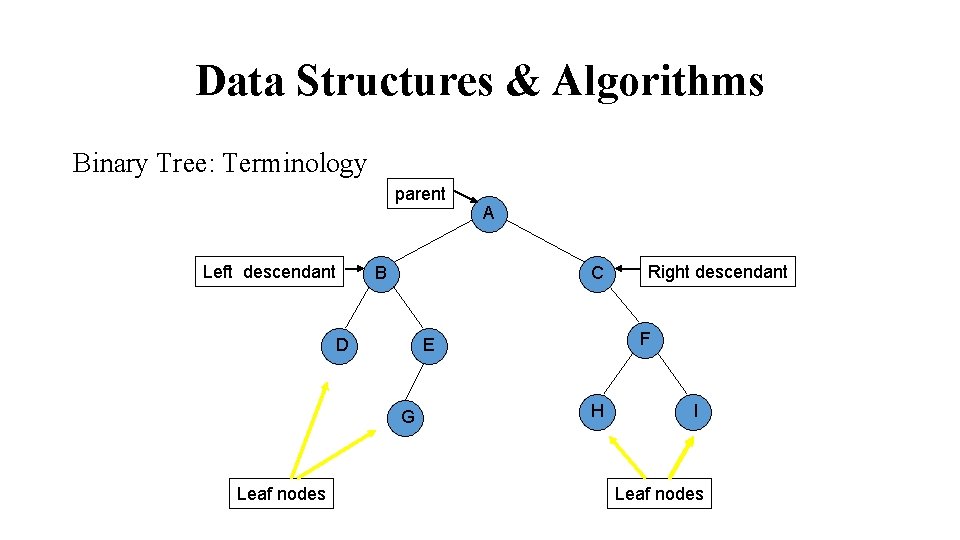
Data Structures & Algorithms Binary Tree: Terminology parent Left descendant B C G Right descendant F E D Leaf nodes A H I Leaf nodes

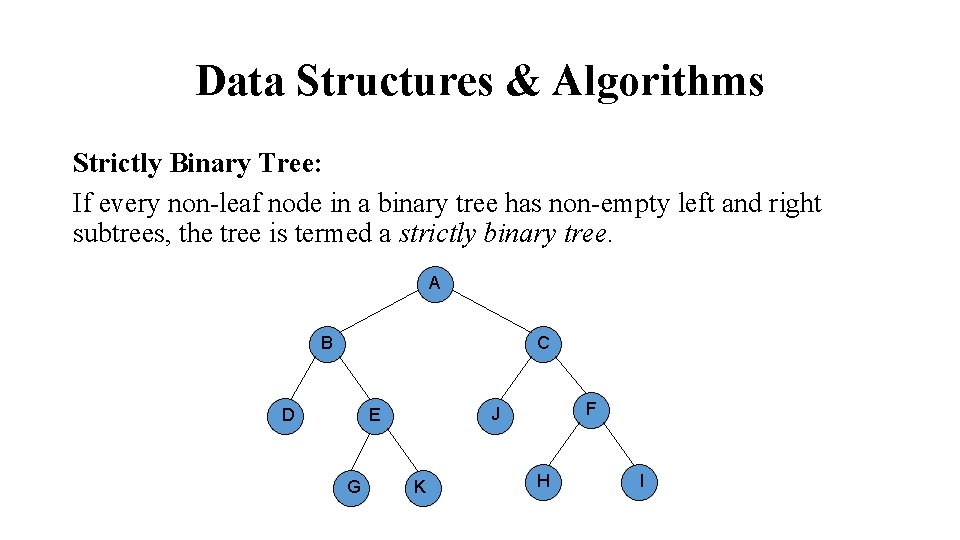
Data Structures & Algorithms Strictly Binary Tree: If every non-leaf node in a binary tree has non-empty left and right subtrees, the tree is termed a strictly binary tree. A B C G F J E D K H I

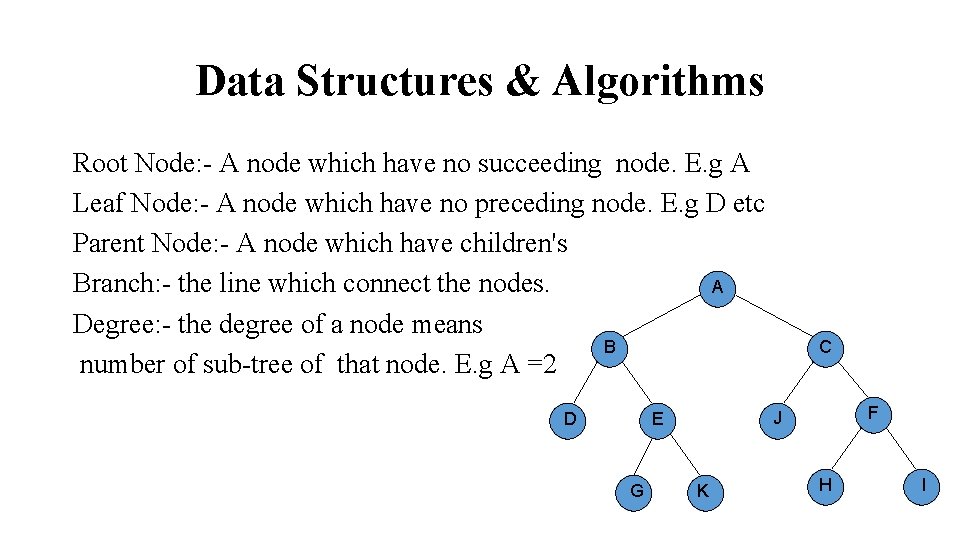
Data Structures & Algorithms Root Node: - A node which have no succeeding node. E. g A Leaf Node: - A node which have no preceding node. E. g D etc Parent Node: - A node which have children's Branch: - the line which connect the nodes. A Degree: - the degree of a node means B number of sub-tree of that node. E. g A =2 G F J E D C K H I

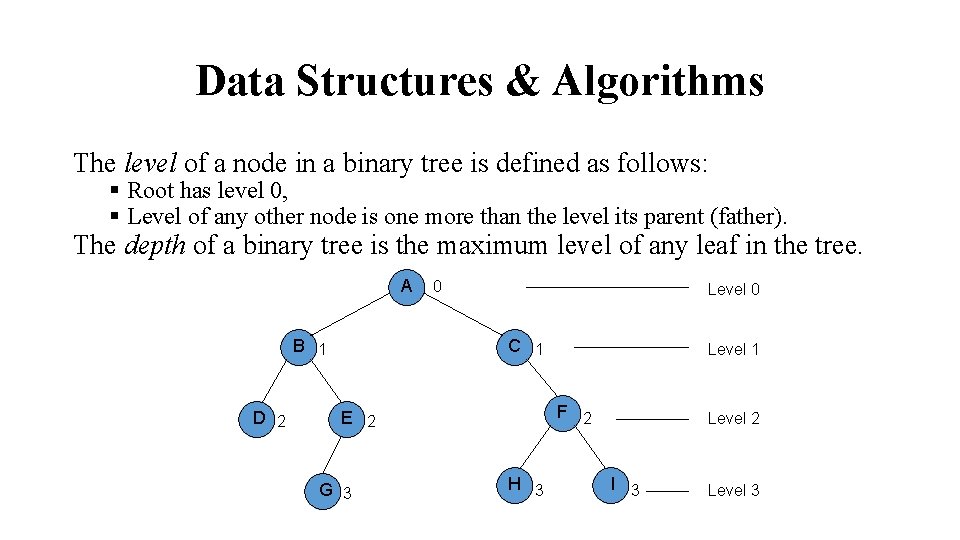
Data Structures & Algorithms The level of a node in a binary tree is defined as follows: § Root has level 0, § Level of any other node is one more than the level its parent (father). The depth of a binary tree is the maximum level of any leaf in the tree. A B 1 D 2 0 Level 0 C 1 F 2 E 2 G 3 Level 1 H 3 Level 2 I 3 Level 3

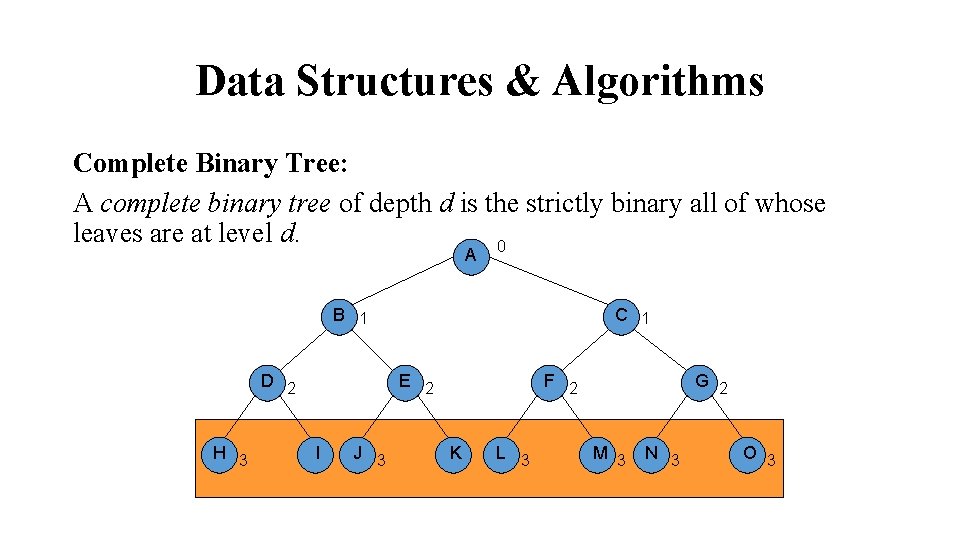
Data Structures & Algorithms Complete Binary Tree: A complete binary tree of depth d is the strictly binary all of whose leaves are at level d. 0 A B 1 D 2 H 3 C 1 E 2 I J 3 F 2 K L 3 G 2 M 3 N 3 O 3

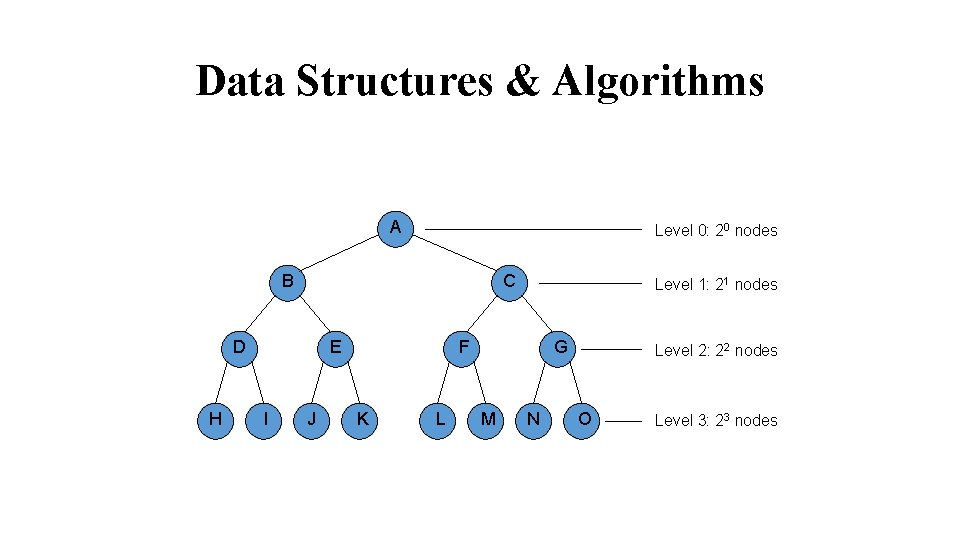
Data Structures & Algorithms A Level 0: 20 nodes B C D H E I J Level 1: 21 nodes F K L G M N Level 2: 22 nodes O Level 3: 23 nodes

Data Structures & Algorithms At level k, there are 2 k nodes. Total number of nodes in the tree of depth d: 20+ 21+ 22 + ………. + 2 d = = 2 d+1 – 1 In a complete binary tree, there are 2 d leaf nodes and (2 d - 1) non-leaf (inner) nodes.

Data Structures & Algorithms If the tree is built out of ‘n’ nodes then n = 2 d+1 – 1 or log 2(n+1) = d+1 or d = log 2(n+1) – 1 I. e. , the depth of the complete binary tree built using ‘n’ nodes will be log 2(n+1) – 1. For example, for n=1, 000, log 2(1000001) is less than 20; the tree would be 20 levels deep. The significance of this shallowness will become evident later.

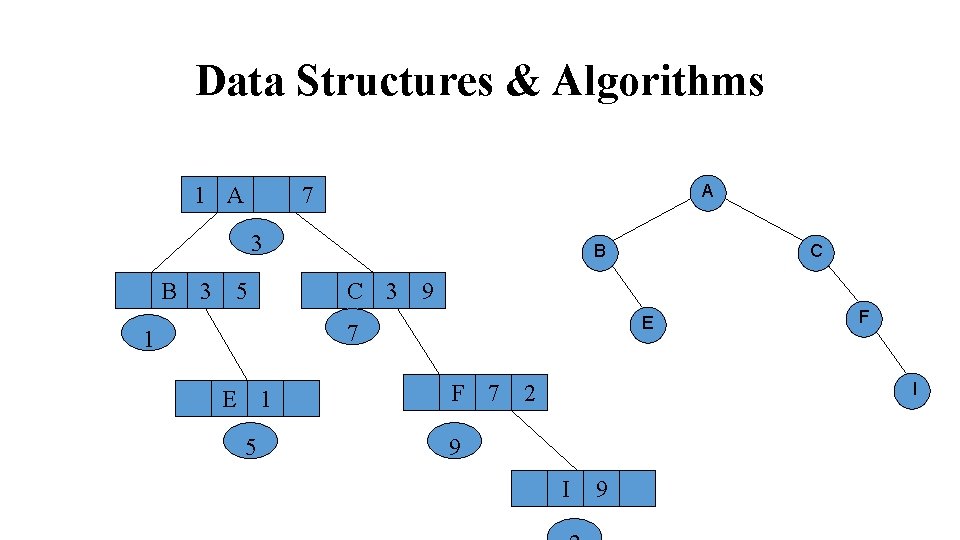
Data Structures & Algorithms Two ways to represents binary tree in memory: 1) Linked List 2) Array Linked List: In linked List representation, three pointers are used which point to left, right, and parent nodes. L Value P R

Data Structures & Algorithms 1 A A 7 3 B 3 5 B C 3 9 E 7 1 E 1 5 C F 7 F I 2 9 I 9

Data Structures & Algorithms Array: 1) The Root is stored in TREE[1]. 2) If a node N occupy TREE[K], then its left child is stored in TREE[2*K] and its right child is stored in TREE[2*K+1]. A C E G G H H F A B C D E D F B

Data Structures & Algorithms There a number of operations that can be defined for a binary tree. If p is pointing to a node in an existing tree then § left(p) returns pointer to the left subtree § right(p) returns pointer to right subtree § parent(p) returns the father of p § brother(p) returns brother of p. § info(p) returns content of the node.

Data Structures & Algorithms In order to construct a binary tree, the following can be useful: set. Left(p, x) creates the left child node of p. The child node contains the info ‘x’. set. Right(p, x) creates the right child node of p. The child node contains the info ‘x’.

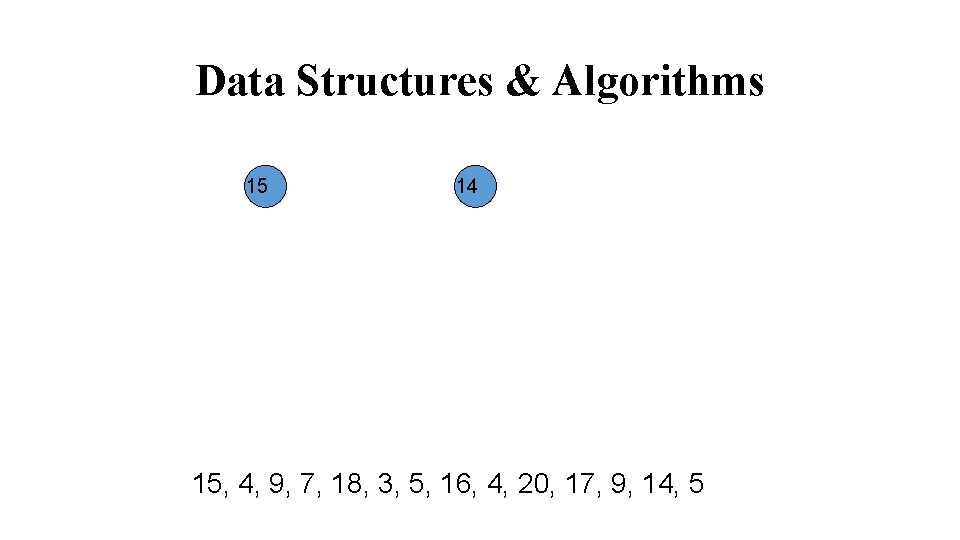
Data Structures & Algorithms Applications of Binary Trees: A binary tree is a useful data structure when two-way decisions must be made at each point in a process. For example, suppose we wanted to find all duplicates in a list of numbers: 14, 15, 4, 9, 7, 18, 3, 5, 16, 4, 20, 17, 9, 14, 5 One way of finding duplicates is to compare each number with all those that precede it. 14, 15, 4, 9, 7, 18, 3, 5, 16, 4, 20, 17, 9, 14, 5

Data Structures & Algorithms If the list of numbers is large and is growing, this procedure involves a large number of comparisons. A linked list could handle the growth but the comparisons would still be large. The number of comparisons can be drastically reduced by using a binary tree. The tree grows dynamically like the linked list.

Data Structures & Algorithms The binary tree is built in a special way. The first number in the list is placed in a node that is designated as the root of a binary tree. Initially, both left and right subtrees of the root are empty. We take the next number and compare it with the number placed in the root. If it is the same then we have a duplicate. Otherwise, we create a new tree node and put the new number in it.

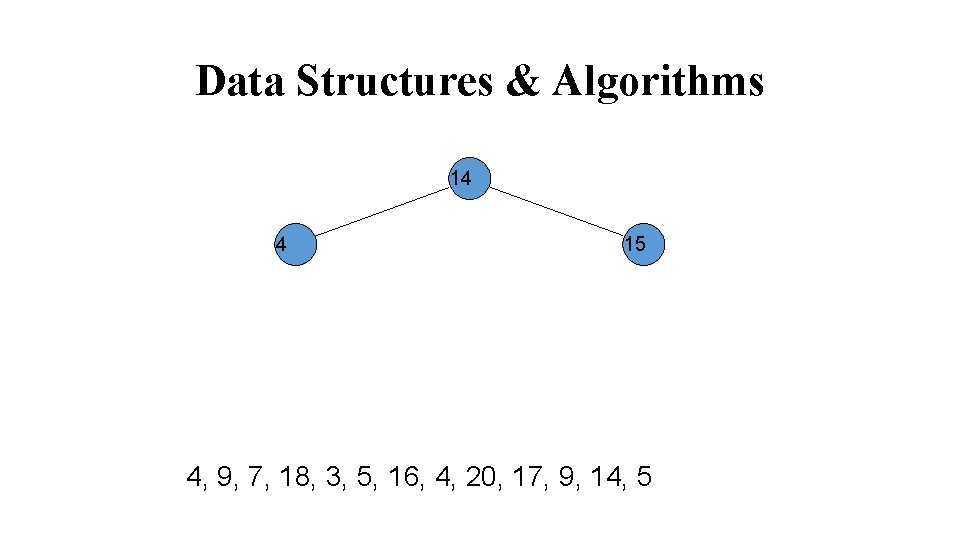
Data Structures & Algorithms The new node is made the left child of the root node if the second number is less than the one in the root. The new node is made the right child if the number is greater than the one in the root. 14 14, 15, 4, 9, 7, 18, 3, 5, 16, 4, 20, 17, 9, 14, 5

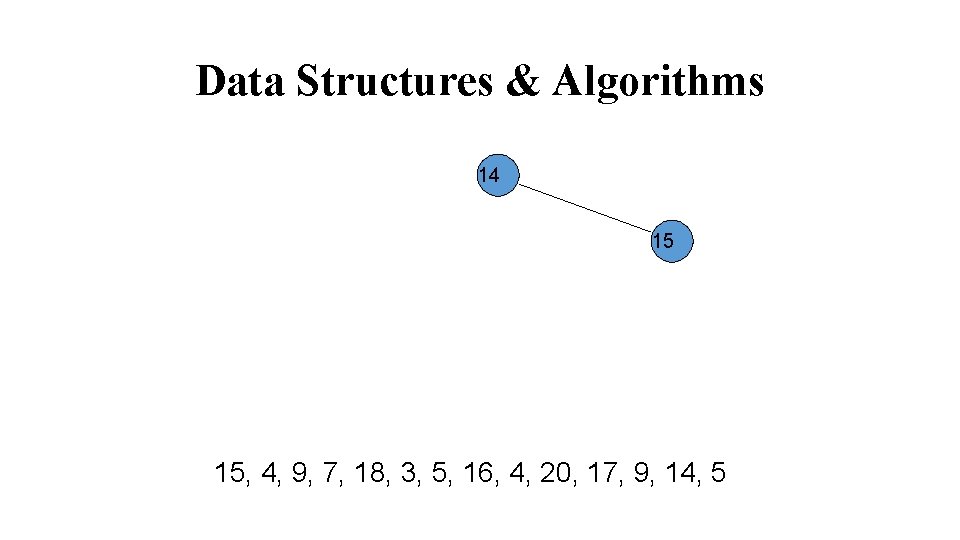
Data Structures & Algorithms 15 14 15, 4, 9, 7, 18, 3, 5, 16, 4, 20, 17, 9, 14, 5

Data Structures & Algorithms 14 15 15, 4, 9, 7, 18, 3, 5, 16, 4, 20, 17, 9, 14, 5

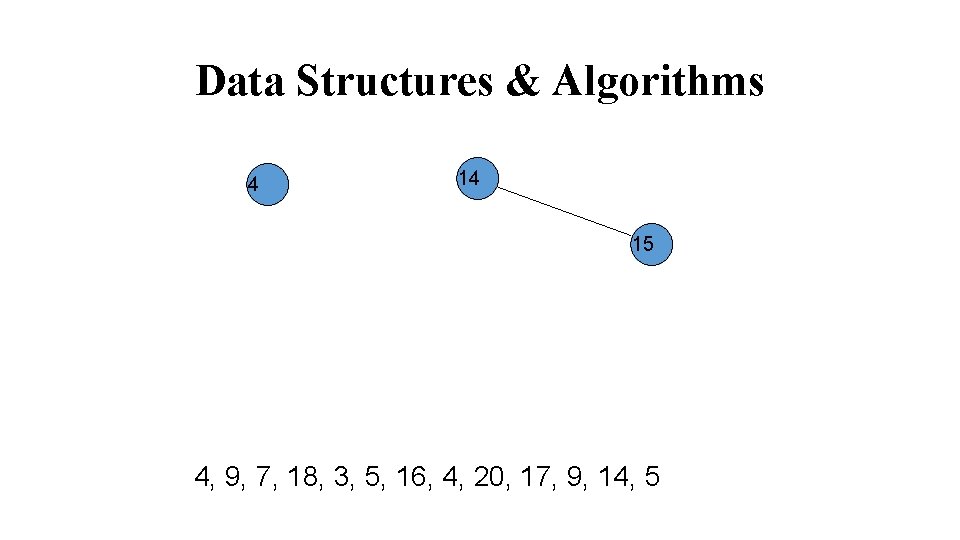
Data Structures & Algorithms 4 14 15 4, 9, 7, 18, 3, 5, 16, 4, 20, 17, 9, 14, 5

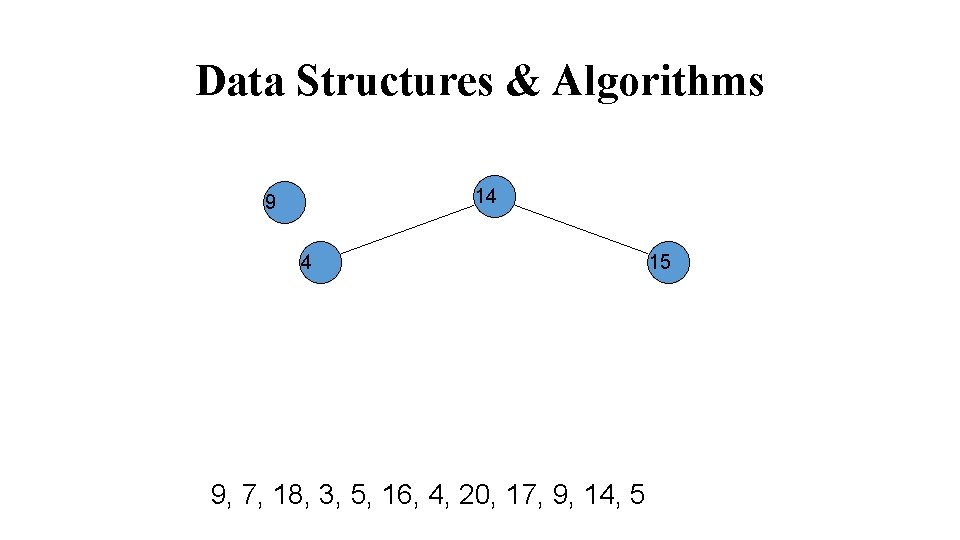
Data Structures & Algorithms 14 4 15 4, 9, 7, 18, 3, 5, 16, 4, 20, 17, 9, 14, 5

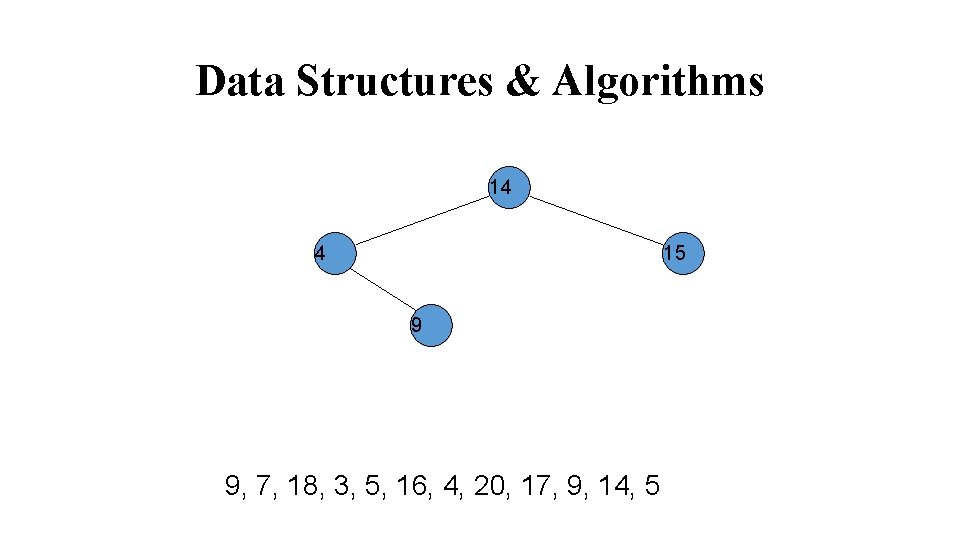
Data Structures & Algorithms 14 9 4 9, 7, 18, 3, 5, 16, 4, 20, 17, 9, 14, 5 15

Data Structures & Algorithms 14 4 15 9 9, 7, 18, 3, 5, 16, 4, 20, 17, 9, 14, 5

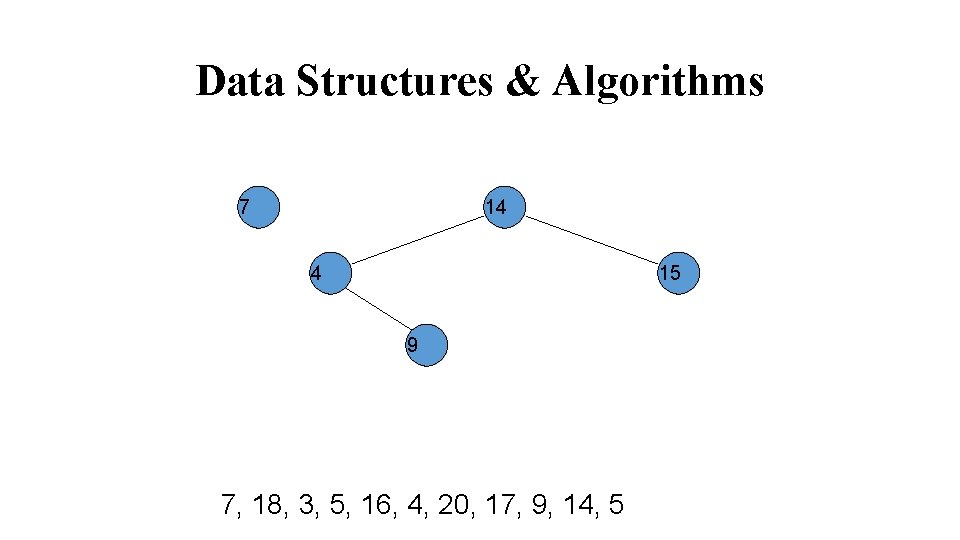
Data Structures & Algorithms 7 14 4 15 9 7, 18, 3, 5, 16, 4, 20, 17, 9, 14, 5

Data Structures & Algorithms 14 4 15 9 7 7, 18, 3, 5, 16, 4, 20, 17, 9, 14, 5

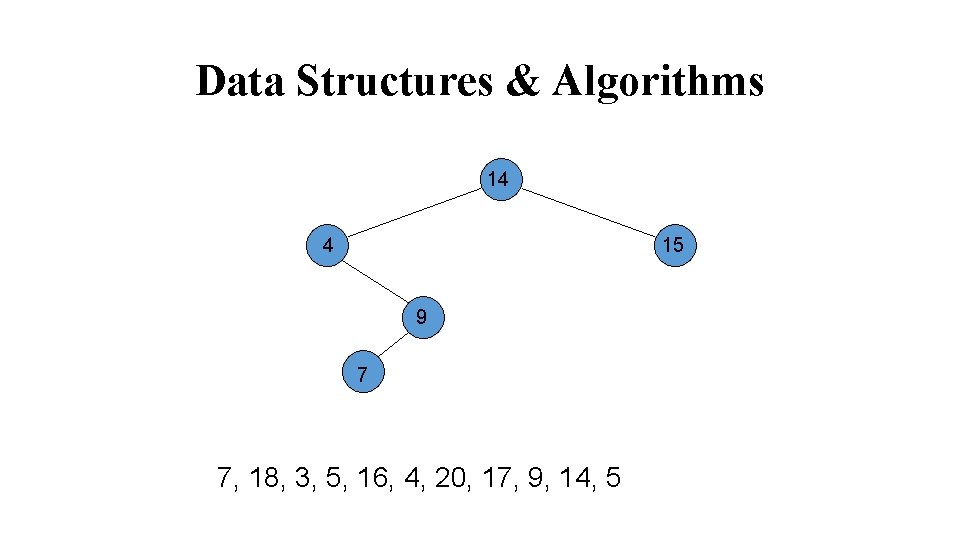
Data Structures & Algorithms 18 14 15 4 9 7 18, 3, 5, 16, 4, 20, 17, 9, 14, 5

Data Structures & Algorithms 14 4 15 9 7 18, 3, 5, 16, 4, 20, 17, 9, 14, 5 18

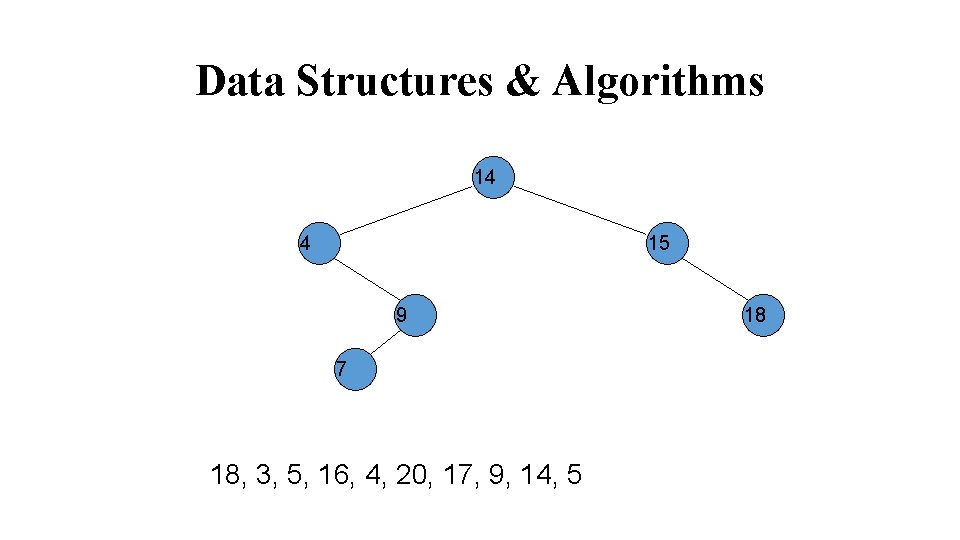
Data Structures & Algorithms 3 14 4 15 9 7 3, 5, 16, 4, 20, 17, 9, 14, 5 18

Data Structures & Algorithms 14 4 15 3 9 7 3, 5, 16, 4, 20, 17, 9, 14, 5 18

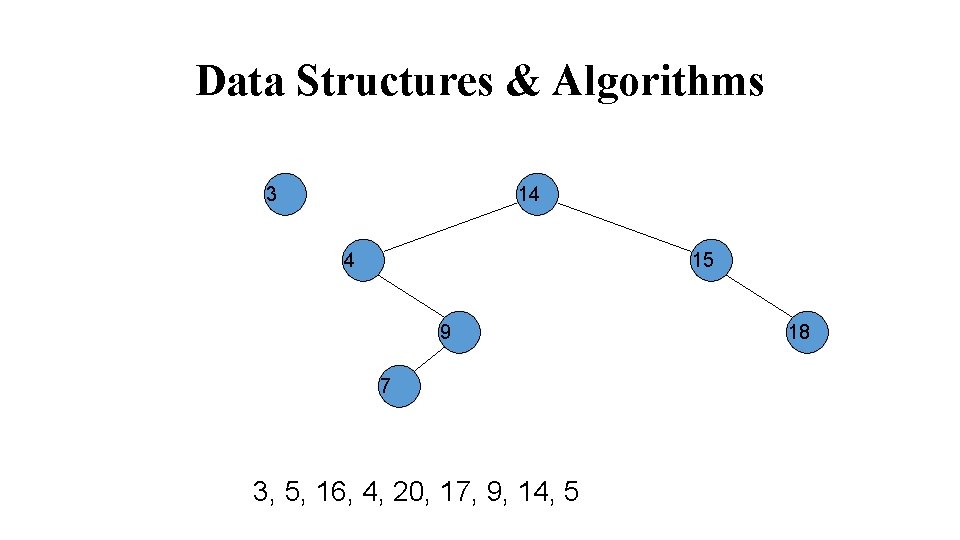
Data Structures & Algorithms 5 14 4 15 3 9 7 5, 16, 4, 20, 17, 9, 14, 5 18

Data Structures & Algorithms 14 4 15 3 9 7 5 5, 16, 4, 20, 17, 9, 14, 5 18

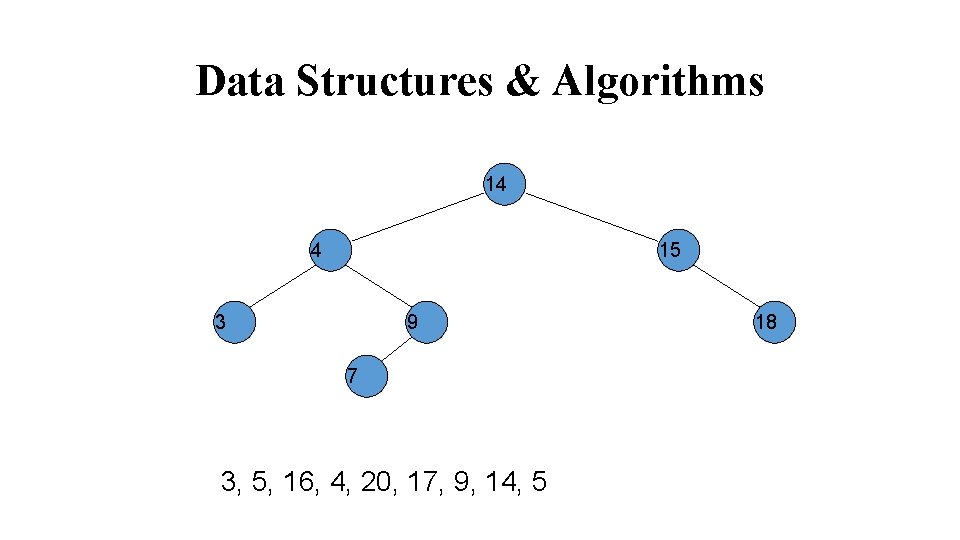
Data Structures & Algorithms 16 14 4 15 3 9 7 5 16, 4, 20, 17, 9, 14, 5 18

Data Structures & Algorithms 14 4 15 3 9 7 5 16, 4, 20, 17, 9, 14, 5 18 16

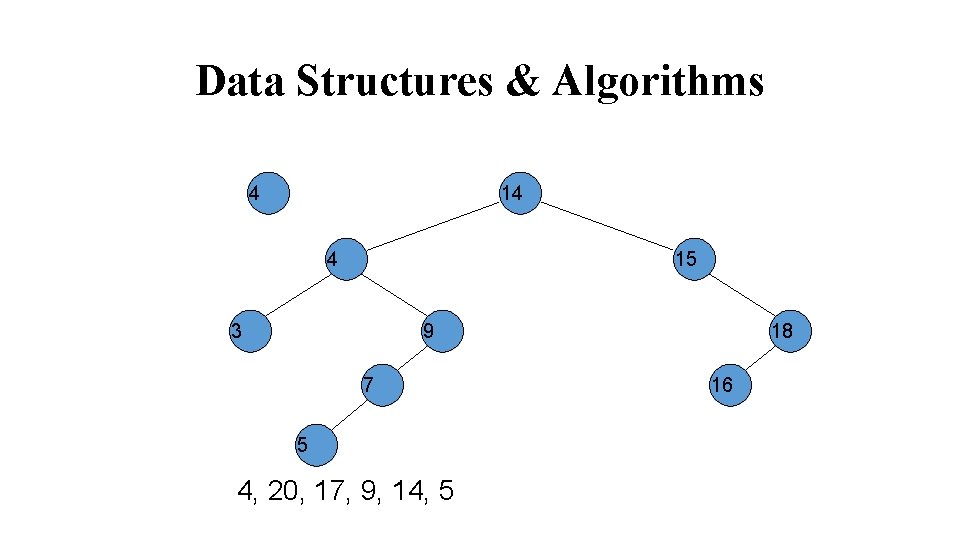
Data Structures & Algorithms 4 14 4 15 3 9 7 5 4, 20, 17, 9, 14, 5 18 16

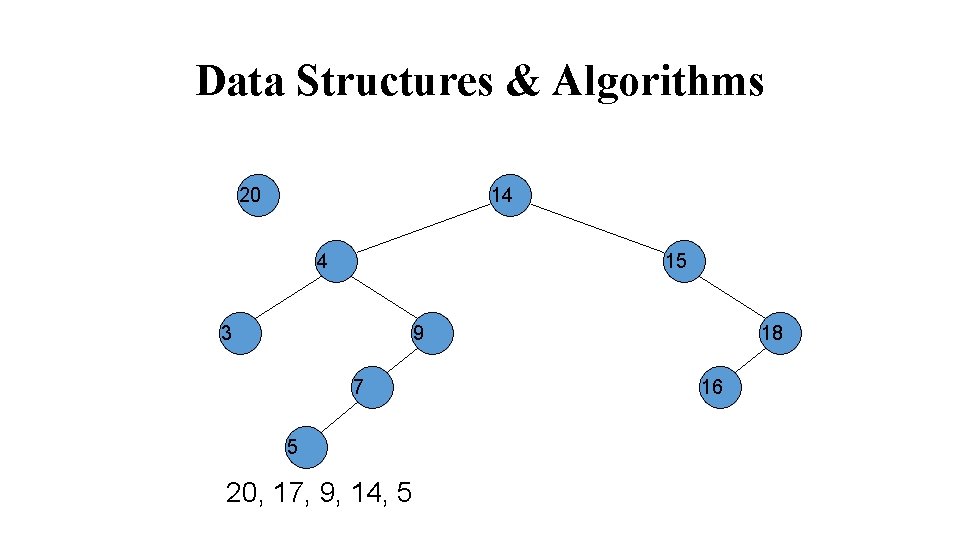
Data Structures & Algorithms 20 14 4 15 3 9 7 5 20, 17, 9, 14, 5 18 16

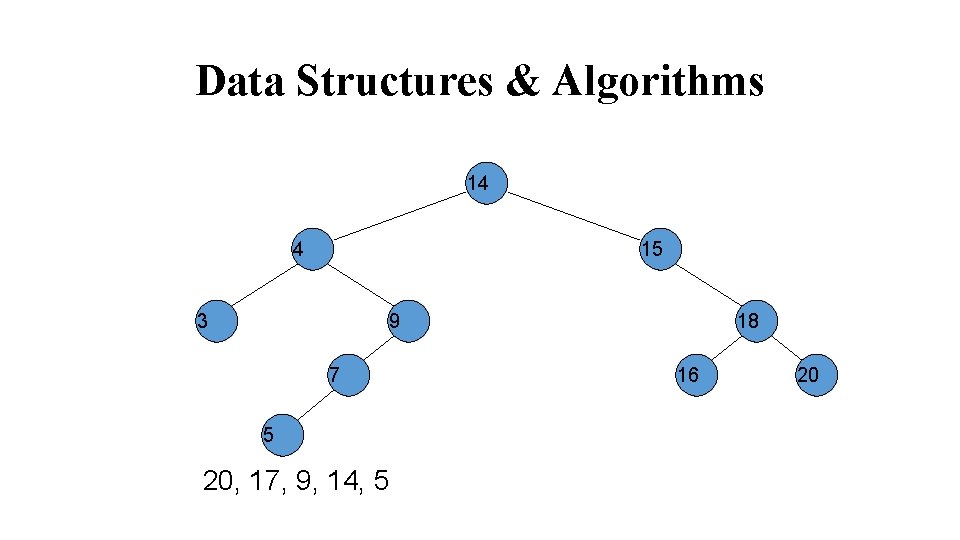
Data Structures & Algorithms 14 4 15 3 9 7 5 20, 17, 9, 14, 5 18 16 20

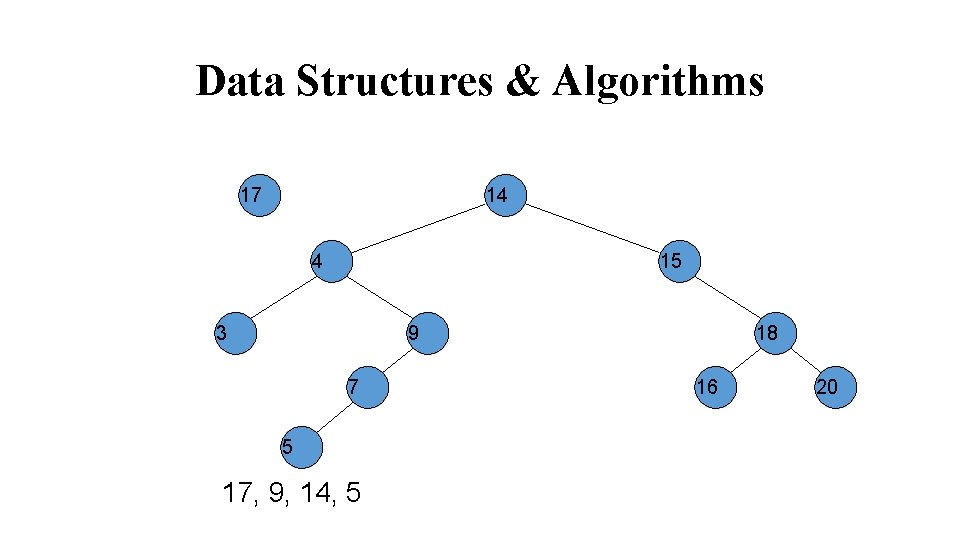
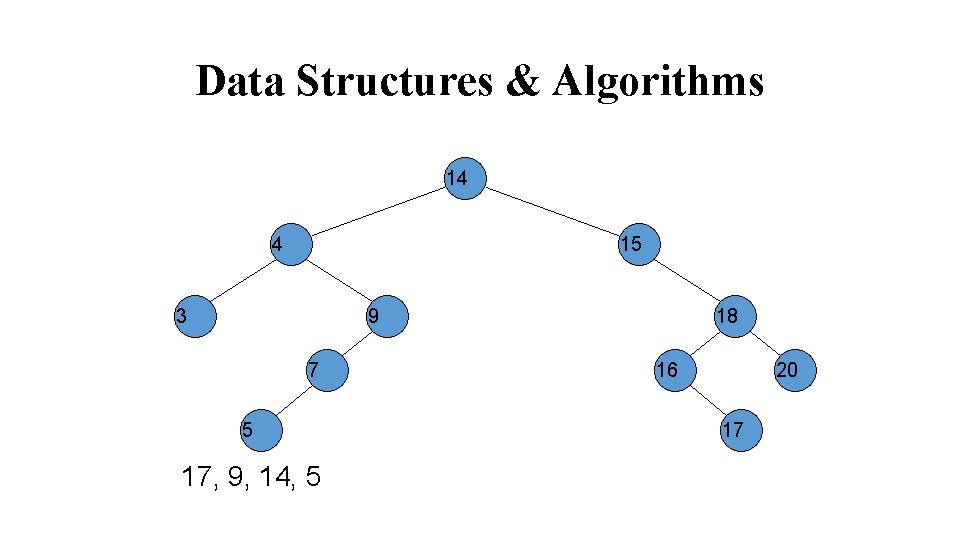
Data Structures & Algorithms 17 14 4 15 3 9 7 5 17, 9, 14, 5 18 16 20

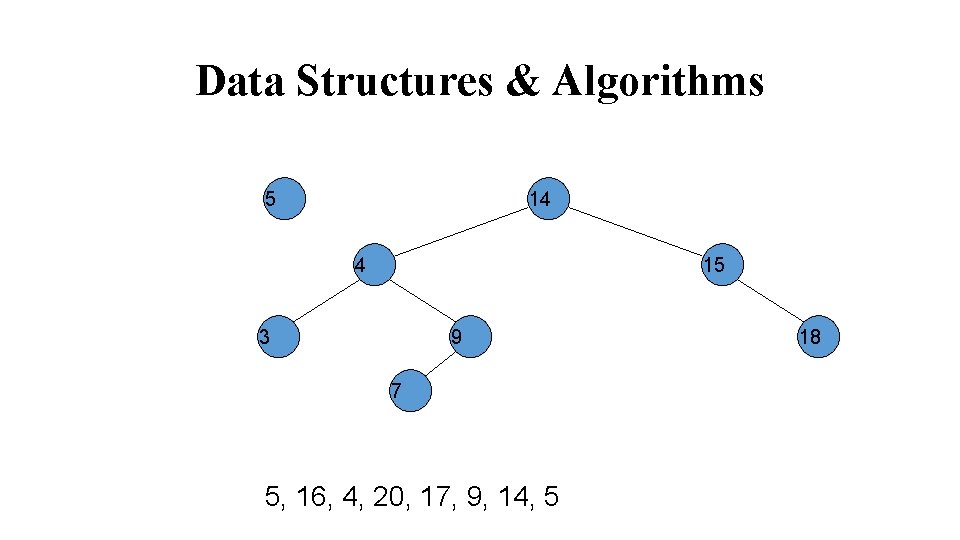
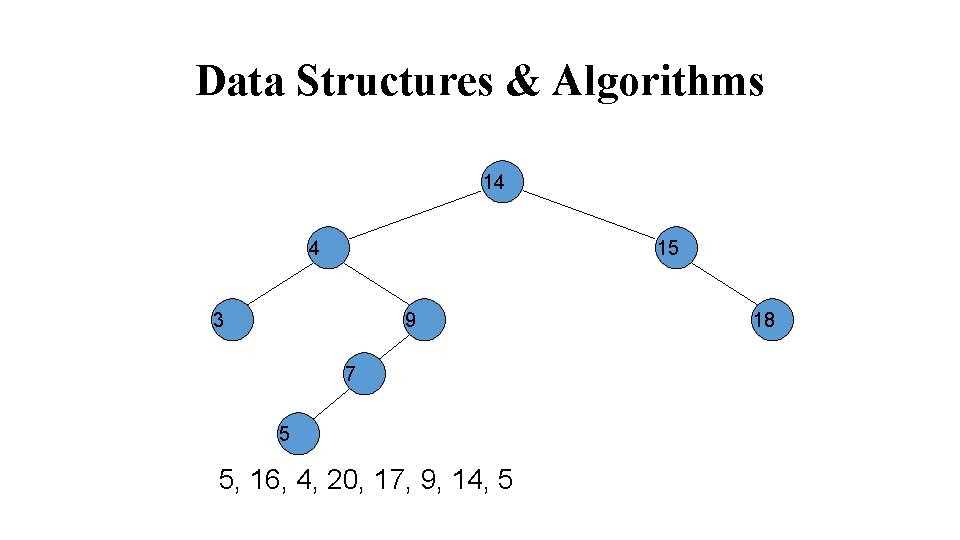
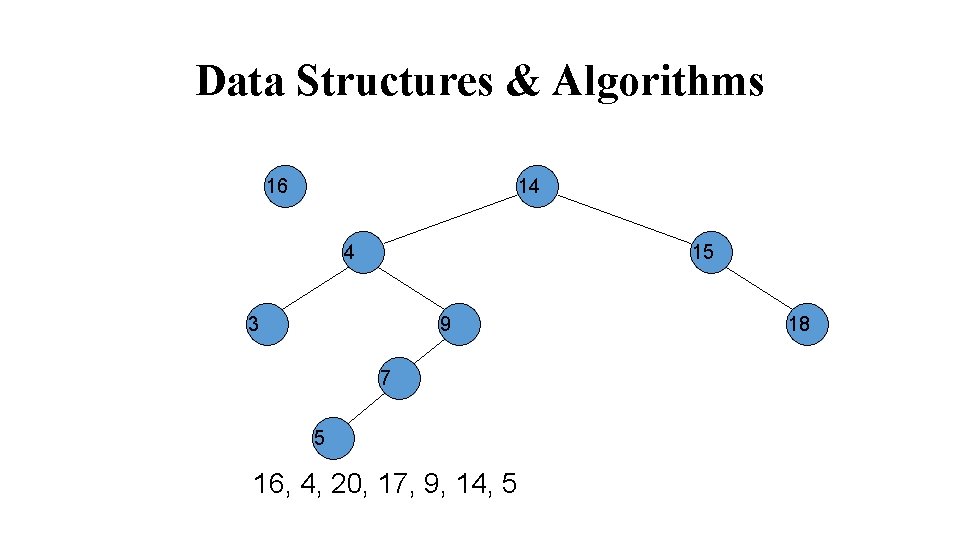
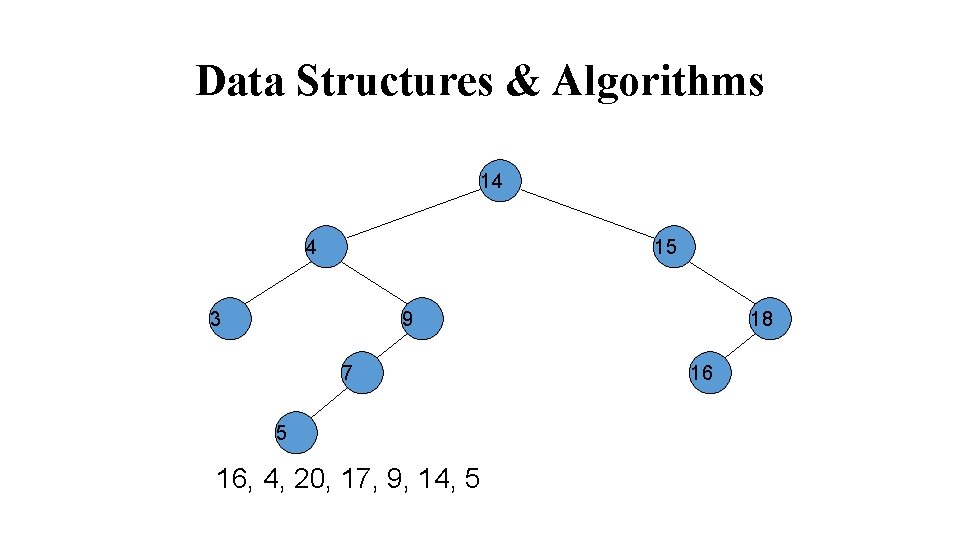
Data Structures & Algorithms 14 4 15 3 9 7 5 17, 9, 14, 5 18 16 20 17

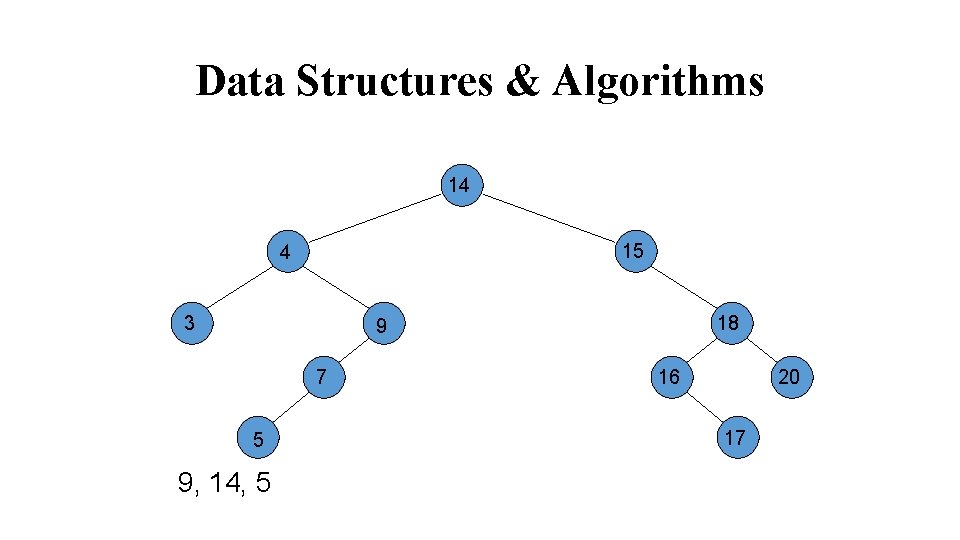
Data Structures & Algorithms 14 15 4 3 18 9 7 5 9, 14, 5 16 20 17

Data Structures & Algorithms #include <stdlib. h> Tree. Node( Object* object ) template <class Object> { class Tree. Node { this->object = object; public: this->left = this->right = NULL; // constructors }; Tree. Node() { this->object = NULL; this->left = this->right = NULL; };

Data Structures & Algorithms Object* get. Info() { return this->object; }; void set. Info(Object* object) { this->object = object; }; Tree. Node* get. Left() { return left; }; void set. Left(Tree. Node *left) { this->left = left; };

Data Structures & Algorithms Tree. Node *get. Right() { return right; }; void set. Right(Tree. Node *right) { this->right = right; }; int is. Leaf( ) { if( this->left == NULL && this->right == NULL) return 1; return 0; };

Data Structures & Algorithms private: Object* object; Tree. Node* left; Tree. Node* right; }; // end class Tree. Node

Data Structures & Algorithms #include <iostream> #include <stdlib. h> #include "Tree. Node. cpp" int main(int argc, char *argv[]) { int x[] = { 14, 15, 4, 9, 7, 18, 3, 5, 16, 4, 20, 17, 9, 14, 5, -1}; Tree. Node<int>* root = new Tree. Node<int>(); root->set. Info( &x[0] ); for(int i=1; x[i] > 0; i++ ) { insert(root, &x[i] ); } }

Data Structures & Algorithms void insert(Tree. Node<int>* root, int* info) { Tree. Node<int>* node = new Tree. Node<int>(info); Tree. Node<int> *p, *q; p = q = root; while( *info != *(p->get. Info()) && q != NULL ) { p = q; if( *info < *(p->get. Info()) ) q = p->get. Left(); else q = p->get. Right(); }

Data Structures & Algorithms if( *info == *(p->get. Info()) ){ cout << "attempt to insert duplicate: " << *info << endl; delete node; } else if( *info < *(p->get. Info()) ) p->set. Left( node ); else p->set. Right( node ); } // end of insert

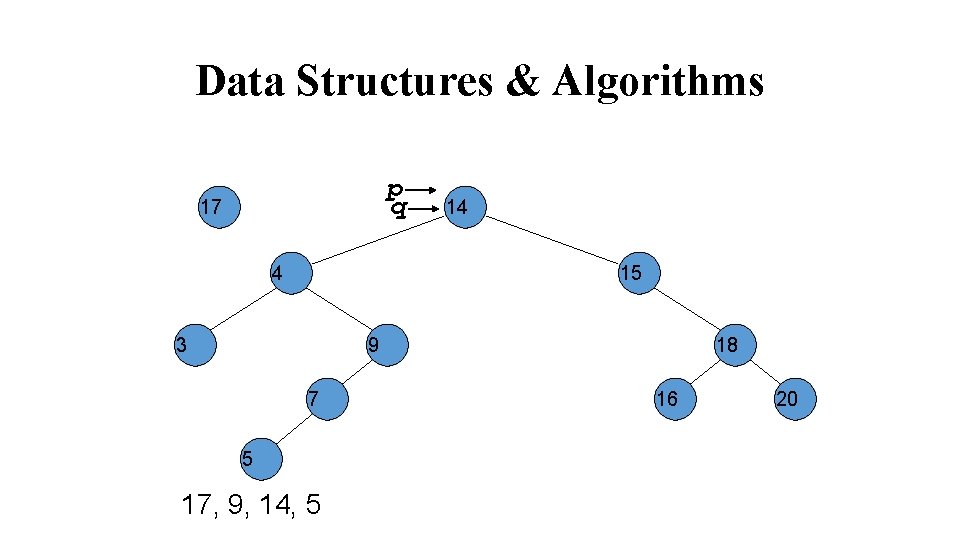
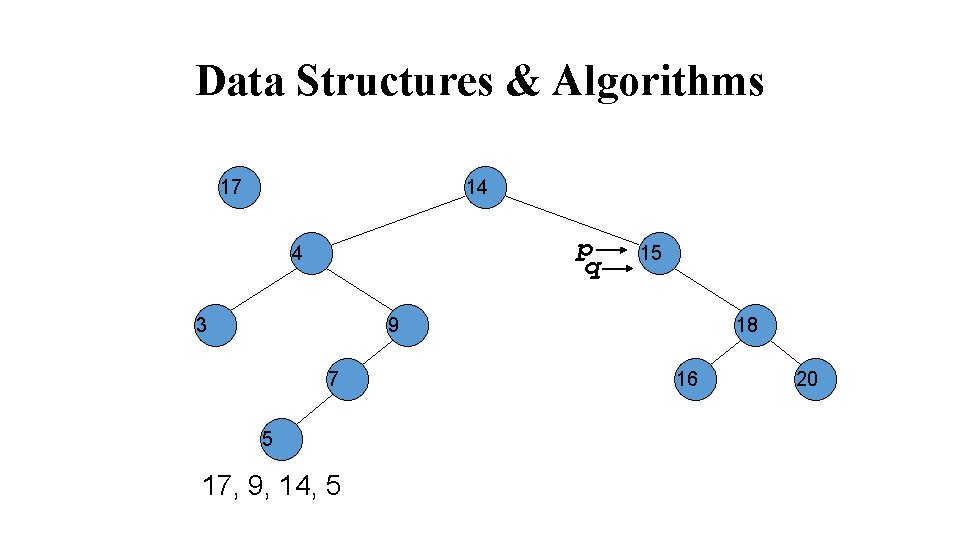
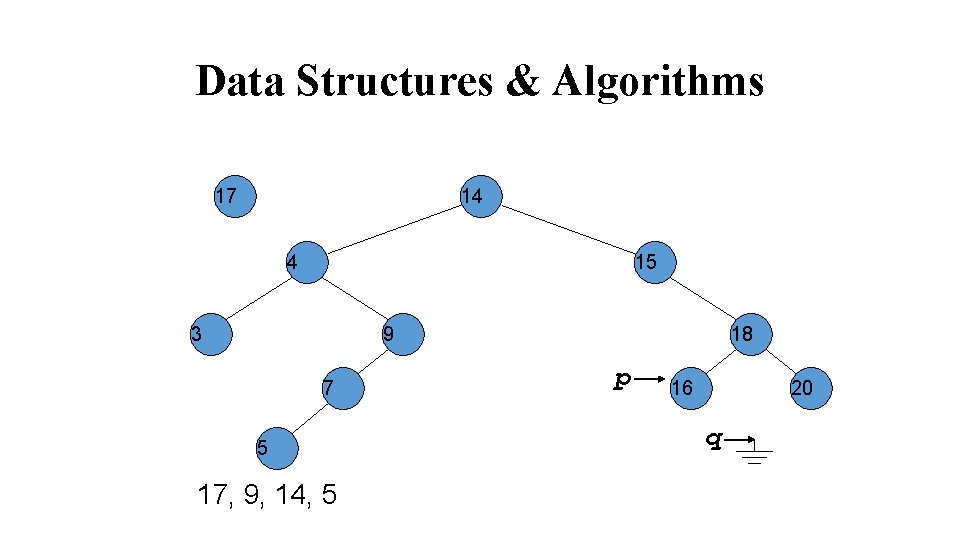
Data Structures & Algorithms p q 17 4 14 15 3 9 7 5 17, 9, 14, 5 18 16 20

Data Structures & Algorithms p 17 4 14 q 3 15 9 7 5 17, 9, 14, 5 18 16 20

Data Structures & Algorithms 17 14 p q 4 3 15 9 7 5 17, 9, 14, 5 18 16 20

Data Structures & Algorithms 17 14 p 4 3 9 7 5 17, 9, 14, 5 15 q 16 18 20

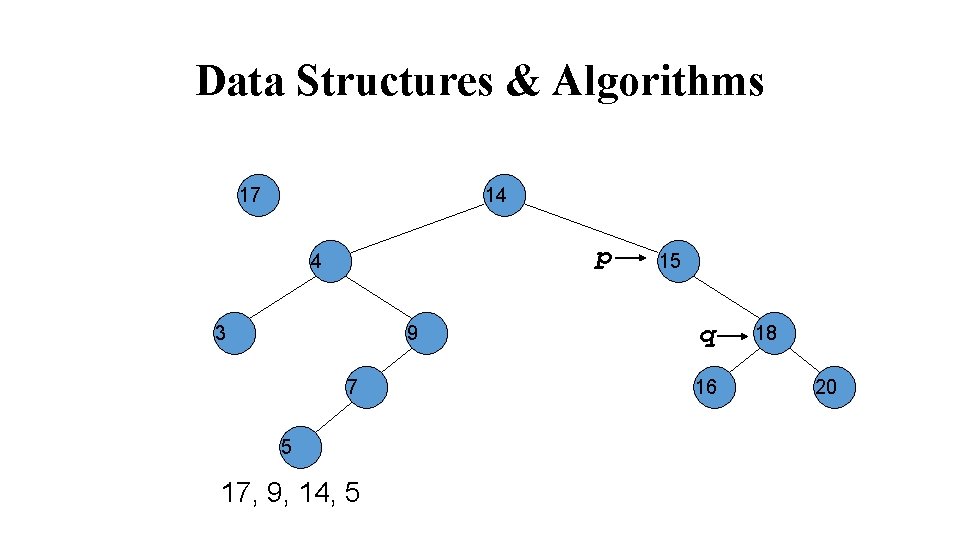
Data Structures & Algorithms 17 14 4 15 3 p 9 7 5 17, 9, 14, 5 q 16 18 20

Data Structures & Algorithms 17 14 4 15 3 9 7 5 17, 9, 14, 5 18 p q 16 20

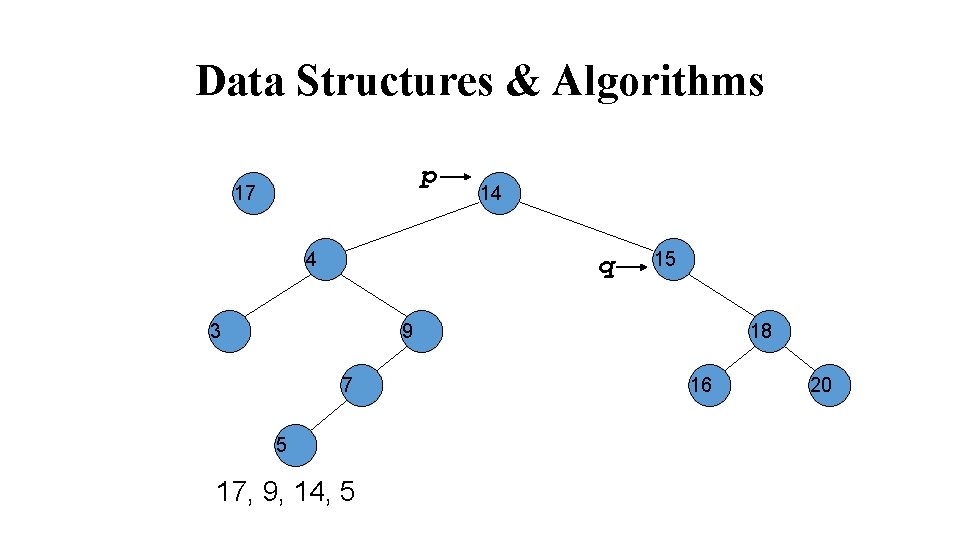
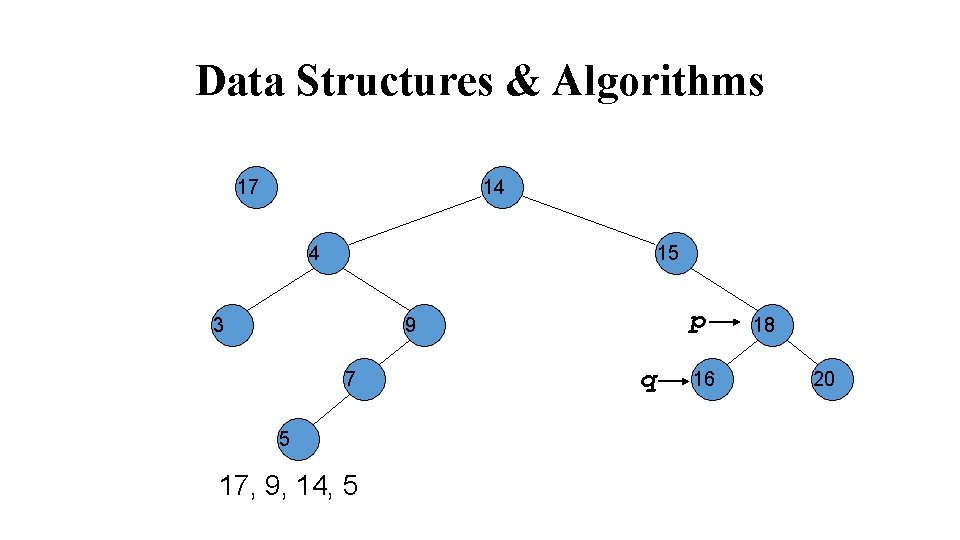
Data Structures & Algorithms 17 14 4 15 3 9 7 5 17, 9, 14, 5 18 p 16 20 q

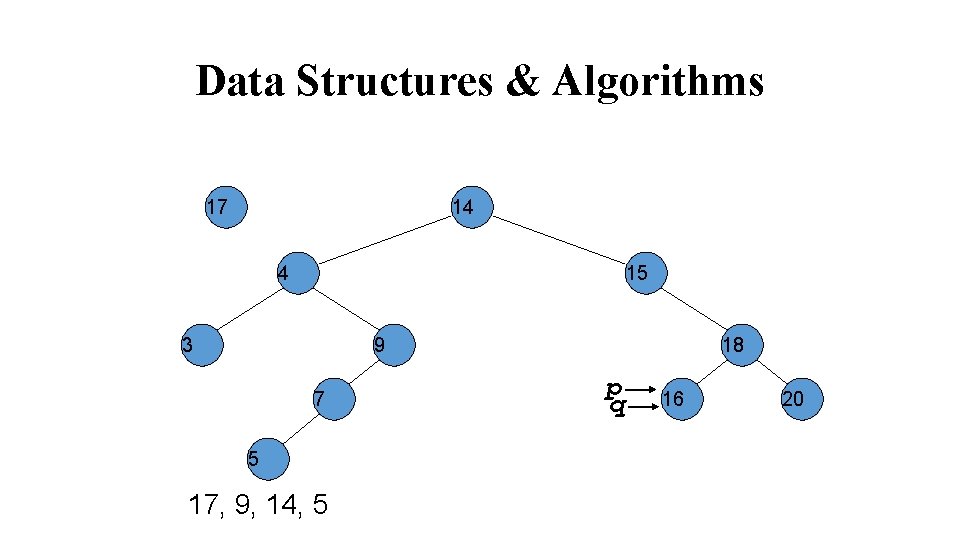
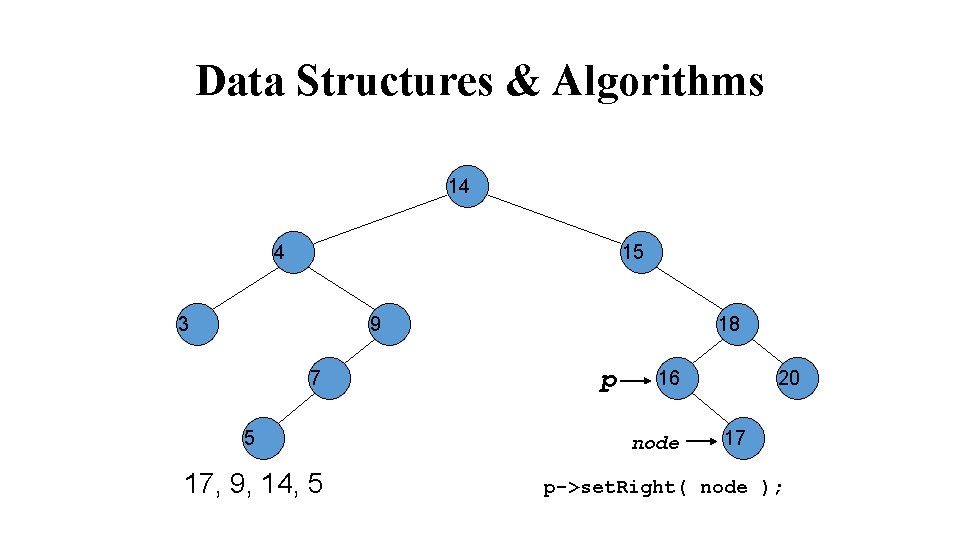
Data Structures & Algorithms 14 4 15 3 9 7 5 17, 9, 14, 5 18 p 16 node 20 17 p->set. Right( node );

Data Structures & Algorithms Cost of Search: Given that a binary tree is level d deep. How long does it take to find out whether a number is already present? Consider the insert(17) in the example tree. Each time around the while loop, we did one comparison. After the comparison, we moved a level down. With the binary tree in place, we can write a routine find(x) that returns true if the number x is present in the tree, false otherwise.

Data Structures & Algorithms How many comparison are needed to find out if x is present in the tree? We do one comparison at each level of the tree until either x is found or q becomes NULL. If the binary tree is built out of n numbers, how many comparisons are needed to find out if a number x is in the tree? Recall that the depth of the complete binary tree built using ‘n’ nodes will be log 2(n+1) – 1. For example, for n=100, 000, log 2(100001) is less than 20; the tree would be 20 levels deep.

Data Structures & Algorithms If the tree is complete binary or nearly complete, searching through 100, 000 numbers will require a maximum of 20 comparisons. Or in general, approximately log 2(n). Compare this with a linked list of 100, 000 numbers. The comparisons required could be a maximum of n.

Data Structures & Algorithms Binary Search Tree: A binary tree with the property that items in the left subtree are smaller than the root and items are larger or equal in the right subtree is called a binary search tree (BST). The tree we built for searching for duplicate numbers was a binary search tree. BST and its variations play an important role in searching algorithms.

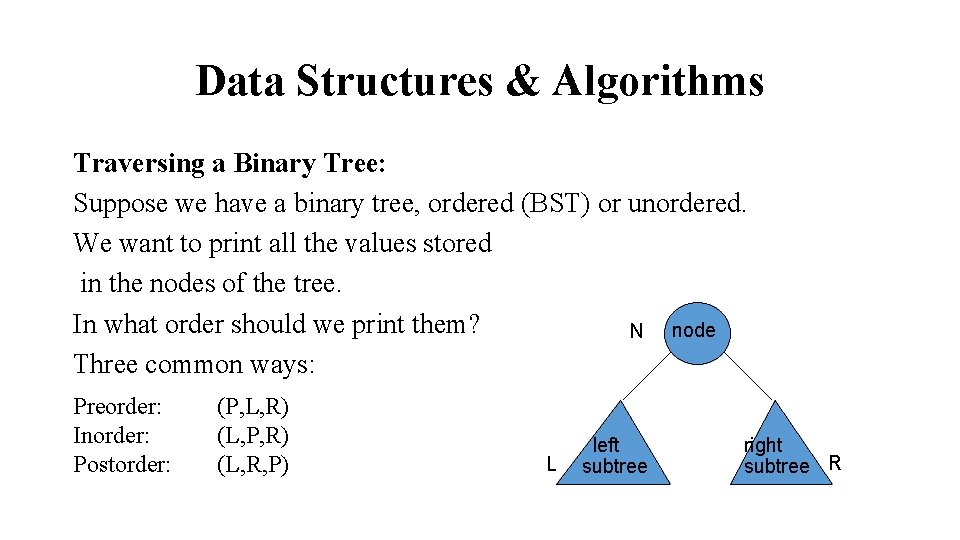
Data Structures & Algorithms Traversing a Binary Tree: Suppose we have a binary tree, ordered (BST) or unordered. We want to print all the values stored in the nodes of the tree. In what order should we print them? N node Three common ways: Preorder: Inorder: Postorder: (P, L, R) (L, P, R) (L, R, P) L left subtree right subtree R

Data Structures & Algorithms void preorder(Tree. Node<int>* tree. Node) { if( tree. Node != NULL ) { cout << *(tree. Node->get. Info())<<" "; preorder(tree. Node->get. Left()); preorder(tree. Node->get. Right()); } }

Data Structures & Algorithms void inorder(Tree. Node<int>* tree. Node) { if( tree. Node != NULL ) { inorder(tree. Node->get. Left()); cout << *(tree. Node->get. Info())<<" "; inorder(tree. Node->get. Right()); } }

Data Structures & Algorithms void postorder(Tree. Node<int>* tree. Node) { if( tree. Node != NULL ) { postorder(tree. Node->get. Left()); postorder(tree. Node->get. Right()); cout << *(tree. Node->get. Info())<<" "; } } cout << "inorder: "; preorder( root); cout << "inorder: "; inorder( root ); cout << "postorder: "; postorder( root );

Data Structures & Algorithms Pre-order Traversal Algorithm: 1. [initially push Null on to STACK and initialize PTR] set TOP=1, STACK[1]=NULL and PTR=Root 2. Repeat 3 to 5 while PTR!=Null 3. Process INFO[PTR] 4. [Right Child? ] if RIGHT[PTR]!=Null then : [Push on STACK] Set TOP=TOP+1; and STACK[TOP]=RIGHT[PTR] end if 5. [Left Child? ] if LEFT[PTR]!=Null then: Set PTR=LEFT[PTR] else Set PTR=STACK[TOP] and TOP=TOP-1 end if end loop 6. exit

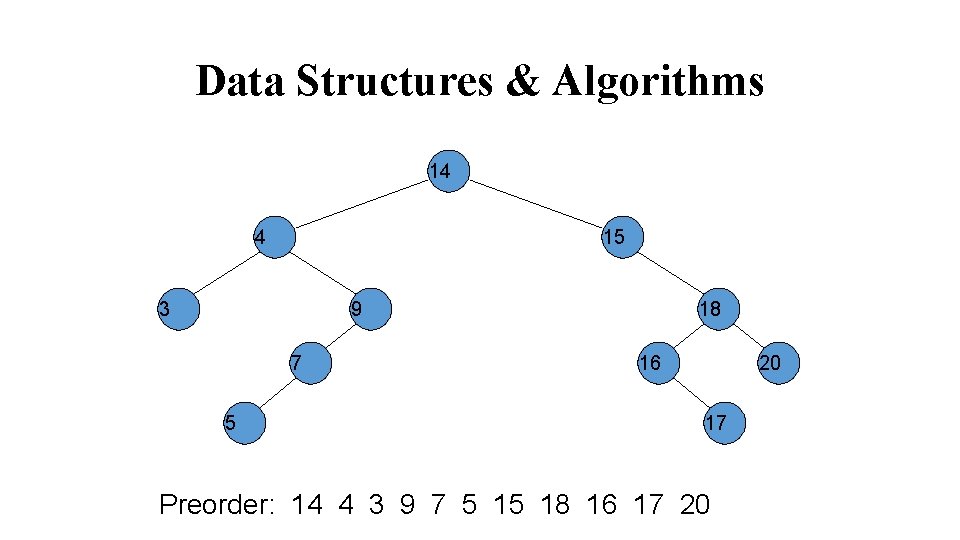
Data Structures & Algorithms 14 4 15 3 9 7 5 18 16 20 17 Preorder: 14 4 3 9 7 5 15 18 16 17 20

Data Structures & Algorithms In-order Traversal Algorithm: 1. [Push Null on to STACK and initialize PTR] set TOP=1, STACK[1]=NULL and PTR=Root 2. Repeat while PTR!=Null [Pushes Left most Path onto STACK] a) set TOP=TOP+1 and STACK[TOP]=PTR b) set PTR=LEFT[PTR] end loop 3. Set PTR=STACK[TOP] & TOP=TOP-1 [pop node from stack] 4. Repeat 5 to 7 while PTR!=Null 5. Process INFO[PTR] 6. [Right Child] if RIGHT[PTR]!=Null, then: a) set PTR=RIGHT[PTR] b) goto step 2 7. Set PTR=STACK[TOP] and TOP=TOP-1 8. Exit

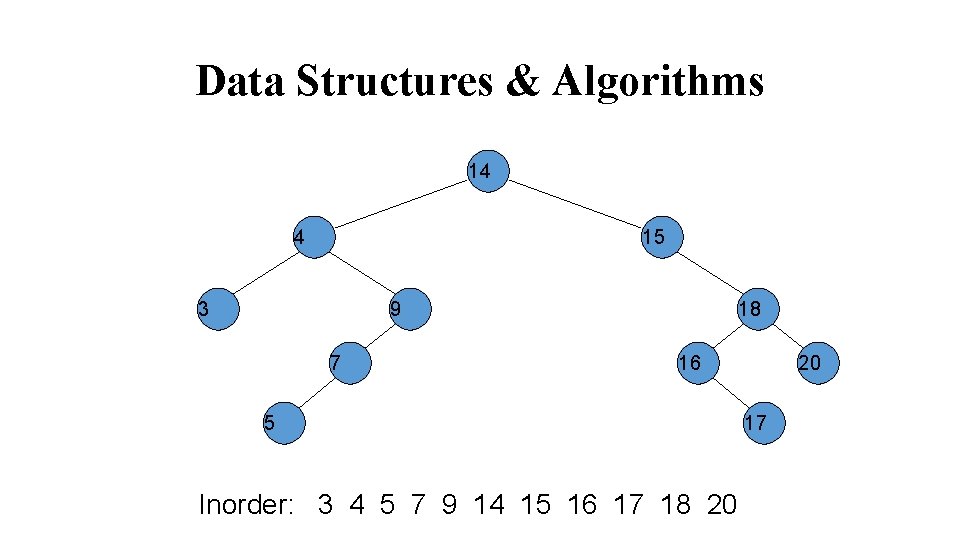
Data Structures & Algorithms 14 4 15 3 9 7 18 16 5 Inorder: 3 4 5 7 9 14 15 16 17 18 20 20 17

Data Structures & Algorithms Post-order Traversal Algorithm 1. [initially push Null on to STACK and initialize PTR] set TOP=1, STACK[1]=NULL and PTR=Root 2. [Push left most path onto STACK] Repeat 3 to 5 while PTR!= Null 3. Set TOP=TOP+1 and STACK[TOP]=PTR [push PTR on Stack] 4. If RIGHT[PTR]!= Null then set TOP=TOP+1 and STACK[TOP]= - RIGHT[PTR] 5. Set PTR=LEFT[PTR] 6. Set PTR=STACK[TOP] & TOP=TOP-1 7. Repeat while PTR>0 a) Process INFO[PTR] b) set PTR=STACK[TOP] & TOP=TOP-1 8. If PTR<0 then: a) set PTR= -PTR b) goto Step 2

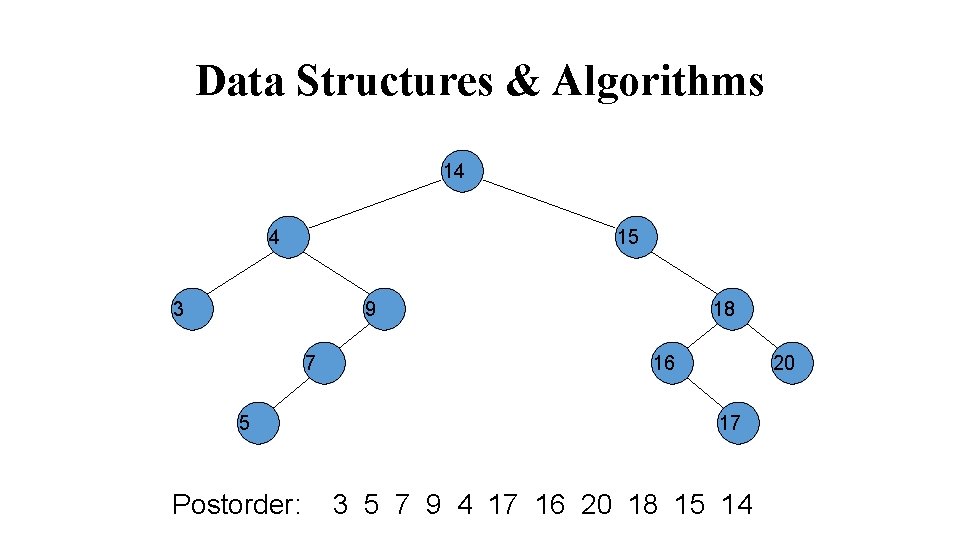
Data Structures & Algorithms 14 4 15 3 9 7 5 Postorder: 18 16 20 17 3 5 7 9 4 17 16 20 18 15 14

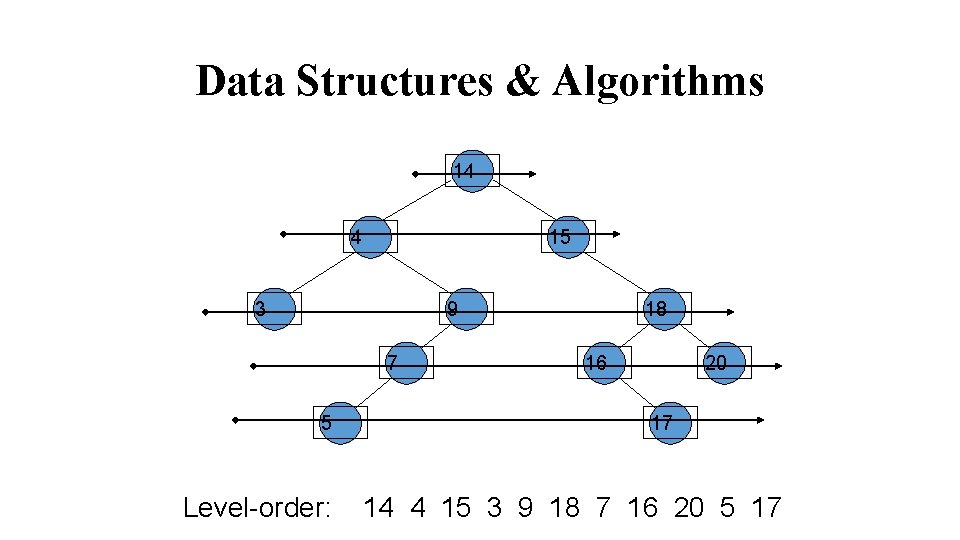
Data Structures & Algorithms Level-order Traversal: There is yet another way of traversing a binary. In level-order traversal, we visit the nodes at each level before proceeding to the next level. At each level, we visit the nodes in a left-to-right order.

Data Structures & Algorithms 14 4 15 3 9 7 5 Level-order: 18 16 20 17 14 4 15 3 9 18 7 16 20 5 17

Data Structures & Algorithms How do we do level-order traversal? Surprisingly, if we use a queue instead of a stack, we can visit the nodes in level-order. Here is the code for level-order traversal:

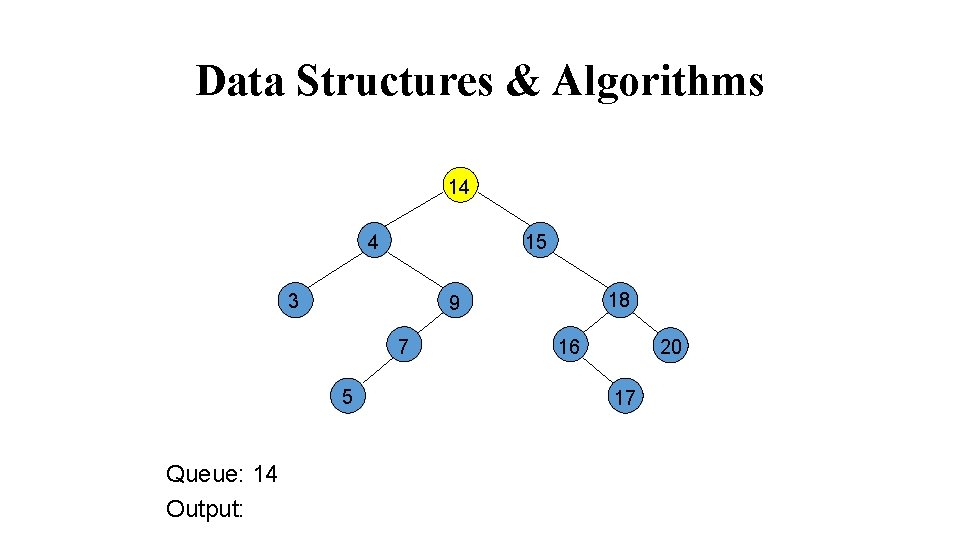
Data Structures & Algorithms void levelorder(Tree. Node<int>* tree. Node) { Queue<Tree. Node<int>* > q; if( tree. Node == NULL ) return; q. enqueue( tree. Node); while( !q. empty() ) { tree. Node = q. dequeue(); cout << *(tree. Node->get. Info()) << " "; if(tree. Node->get. Left() != NULL ) q. enqueue( tree. Node->get. Left()); if(tree. Node->get. Right() != NULL ) q. enqueue( tree. Node->get. Right()); } cout << endl; }

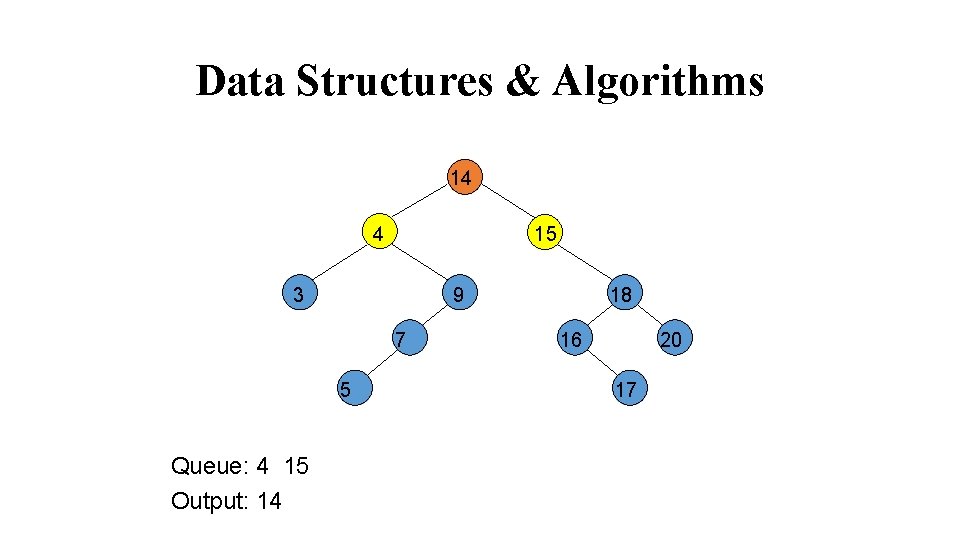
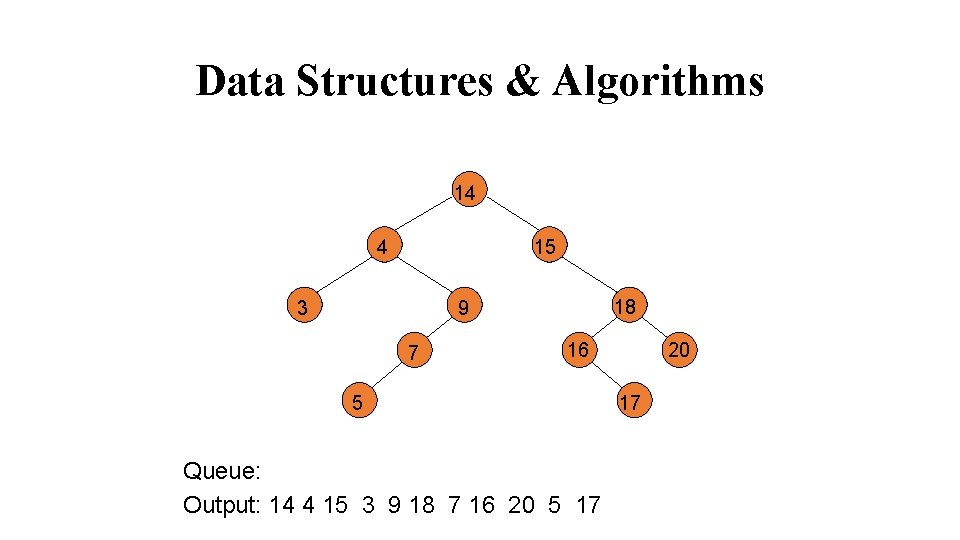
Data Structures & Algorithms 14 4 15 3 7 5 Queue: 14 Output: 18 9 20 16 17

Data Structures & Algorithms 14 4 15 3 9 7 5 Queue: 4 15 Output: 14 18 16 20 17

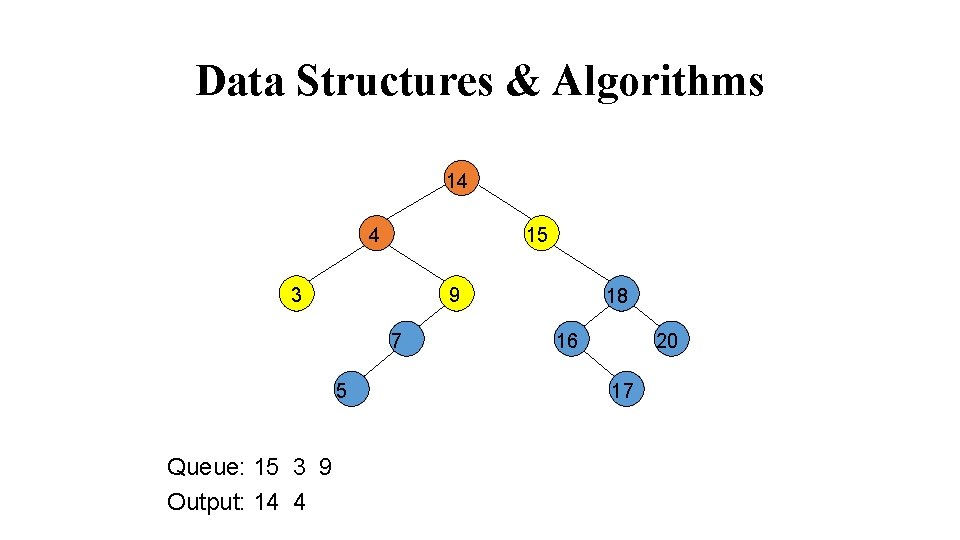
Data Structures & Algorithms 14 4 15 3 9 7 5 Queue: 15 3 9 Output: 14 4 18 16 20 17

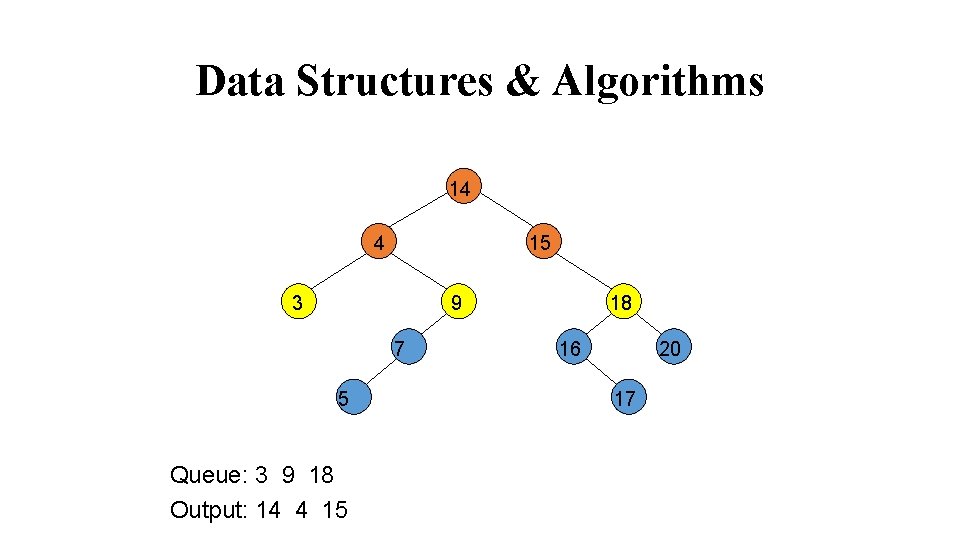
Data Structures & Algorithms 14 4 15 3 9 7 5 Queue: 3 9 18 Output: 14 4 15 18 16 20 17

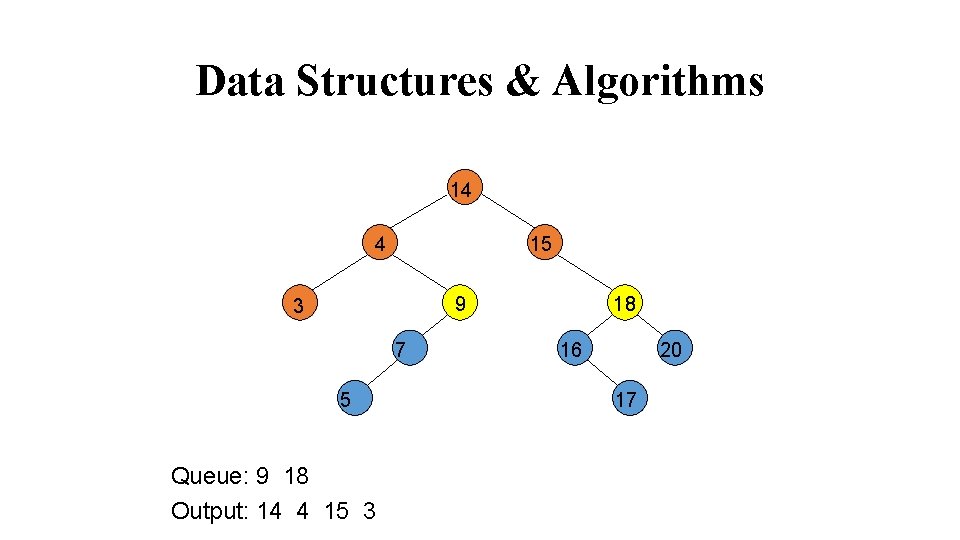
Data Structures & Algorithms 14 4 15 18 9 3 7 5 Queue: 9 18 Output: 14 4 15 3 16 20 17

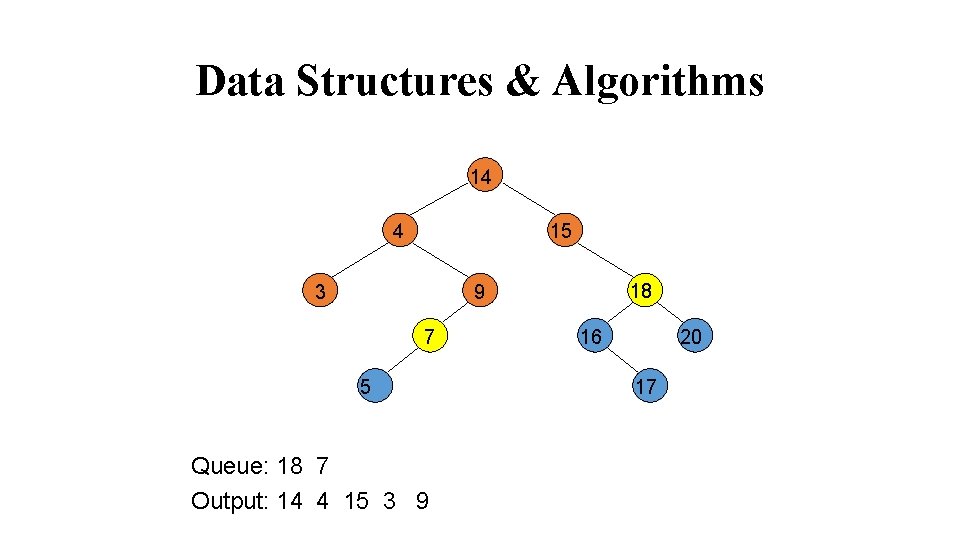
Data Structures & Algorithms 14 4 15 3 18 9 7 5 Queue: 18 7 Output: 14 4 15 3 9 16 20 17

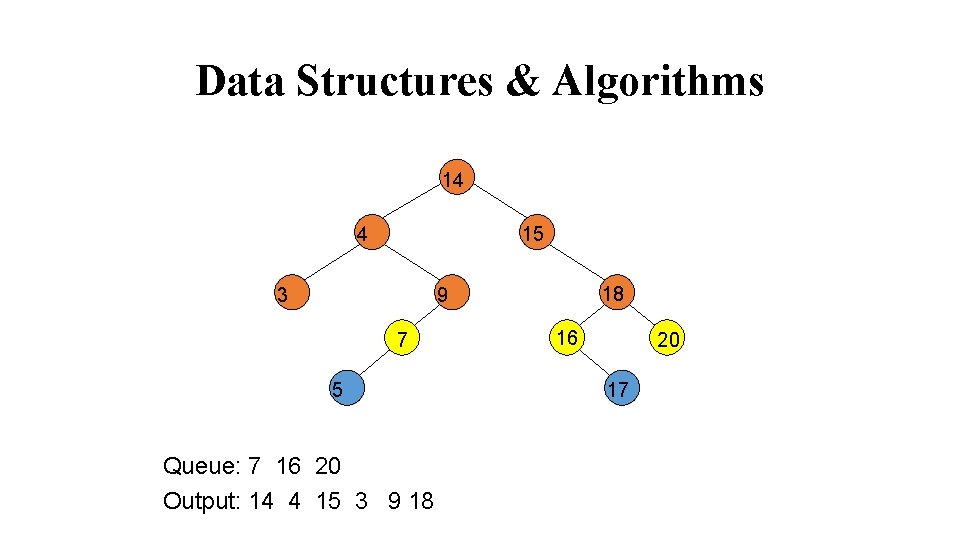
Data Structures & Algorithms 14 4 15 3 18 9 7 5 Queue: 7 16 20 Output: 14 4 15 3 9 18 16 20 17

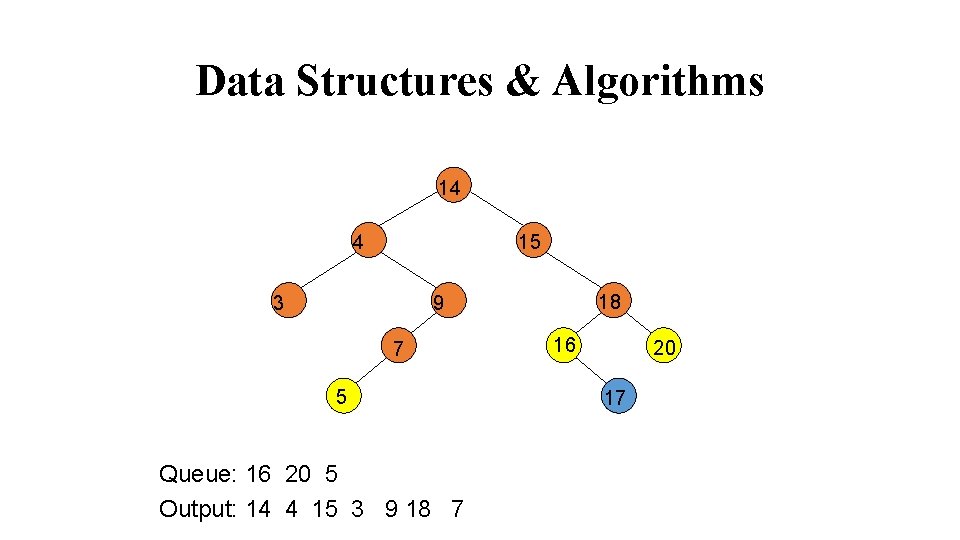
Data Structures & Algorithms 14 4 15 3 18 9 7 5 Queue: 16 20 5 Output: 14 4 15 3 9 18 7 16 20 17

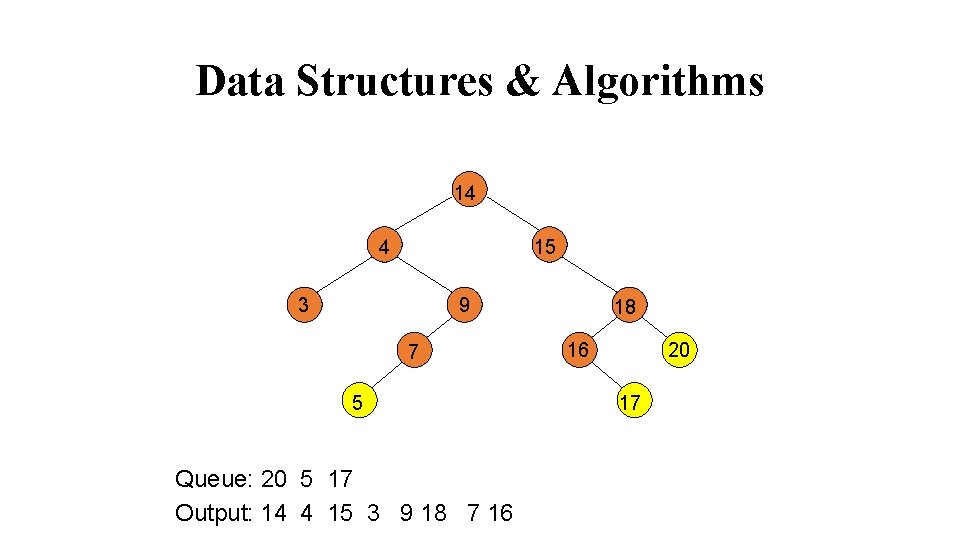
Data Structures & Algorithms 14 4 15 9 3 7 5 Queue: 20 5 17 Output: 14 4 15 3 9 18 7 16 18 16 20 17

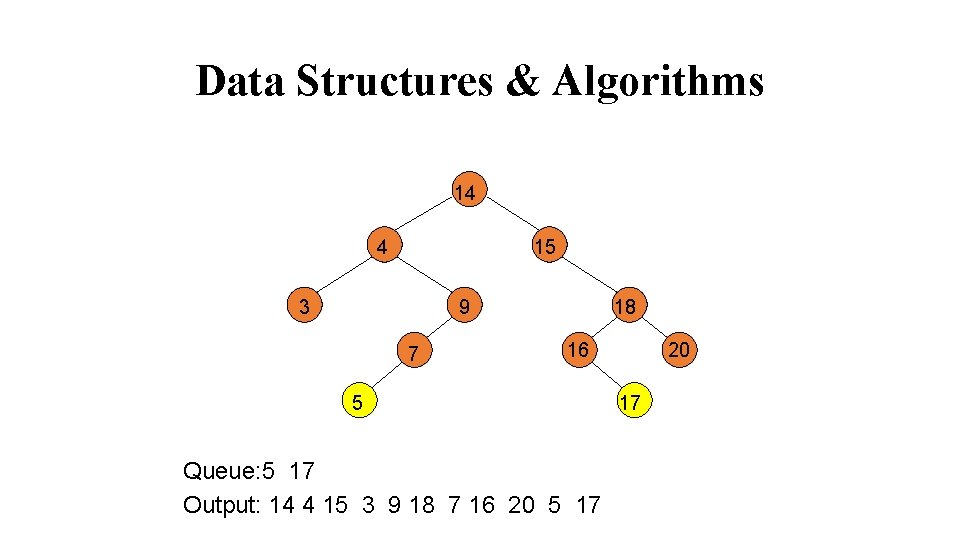
Data Structures & Algorithms 14 4 15 9 3 7 18 16 5 Queue: 5 17 Output: 14 4 15 3 9 18 7 16 20 5 17 20 17

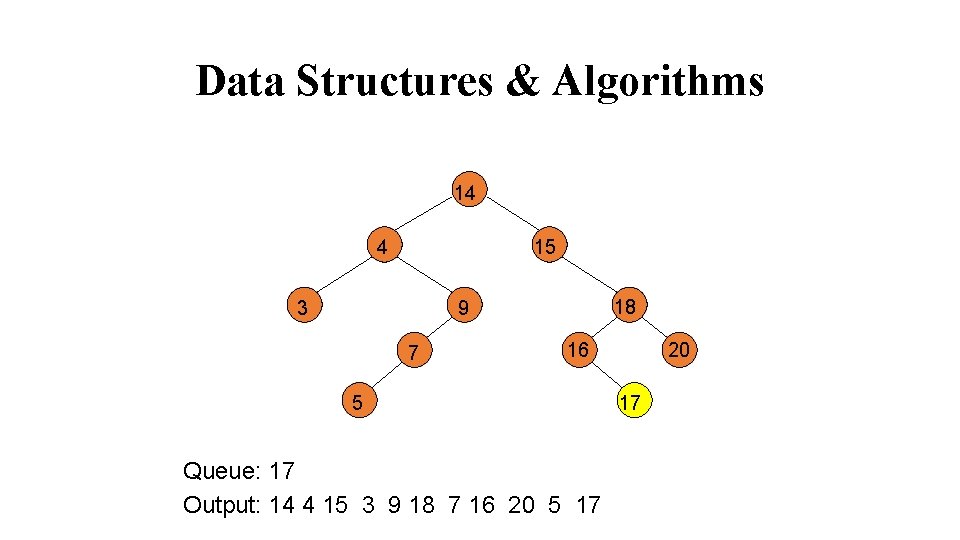
Data Structures & Algorithms 14 4 15 3 18 9 7 16 5 Queue: 17 Output: 14 4 15 3 9 18 7 16 20 5 17 20 17

Data Structures & Algorithms 14 4 15 3 18 9 7 16 5 Queue: Output: 14 4 15 3 9 18 7 16 20 5 17 20 17

Data Structures & Algorithms Storing other Type of Data: The examples of binary trees so far have been storing integer data in the tree node. This is surely not a requirement. Any type of data can be stored in a tree node. Here, for example, is the C++ code to build a tree with character strings.

Data Structures & Algorithms void word. Tree() { Tree. Node<char>* root = new Tree. Node<char>(); static char* word[] = "babble", "fable", "jacket", "backup", "eagle", "daily", "gain", "bandit", "abandon", "abash", "accuse", "economy", "adhere", "advise", "cease", "debunk", "feeder", "genius", "fetch", "chain", NULL}; root->set. Info( word[0] ); for(i=1; word[i]; i++ ) insert(root, word[i] ); inorder( root ); cout << endl; }

Data Structures & Algorithms void insert(Tree. Node<char>* root, char* info) { Tree. Node<char>* node = new Tree. Node<char>(info); Tree. Node<char> *p, *q; p = q = root; while( strcmp(info, p->get. Info()) != 0 && q != NULL ) { p = q; if( strcmp(info, p->get. Info()) < 0 ) q = p->get. Left(); else q = p->get. Right(); }

Data Structures & Algorithms if( strcmp(info, p->get. Info()) == 0 ){ cout << "attempt to insert duplicate: " << *info << endl; delete node; } else if( strcmp(info, p->get. Info()) < 0 ) p->set. Left( node ); else p->set. Right( node ); }

Data Structures & Algorithms Output: abandon abash accuse adhere advise babble backup bandit cease chain daily debunk eagle economy fable feeder fetch gain genius jacket

Data Structures & Algorithms Notice that the words are sorted in increasing order when we traversed the tree in inorder manner. This should not come as a surprise if you consider how we built the BST. For a given root node, values less than the info in the node were all in the left subtree and values greater or equal were in the right. Inorder prints the left subtree, then the node finally the right subtree. Building a BST and doing an inorder traversal leads to a sorting algorithm. abandon abash accuse adhere advise babble backup bandit cease chain daily debunk eagle economy fable feeder fetch gain genius jacket

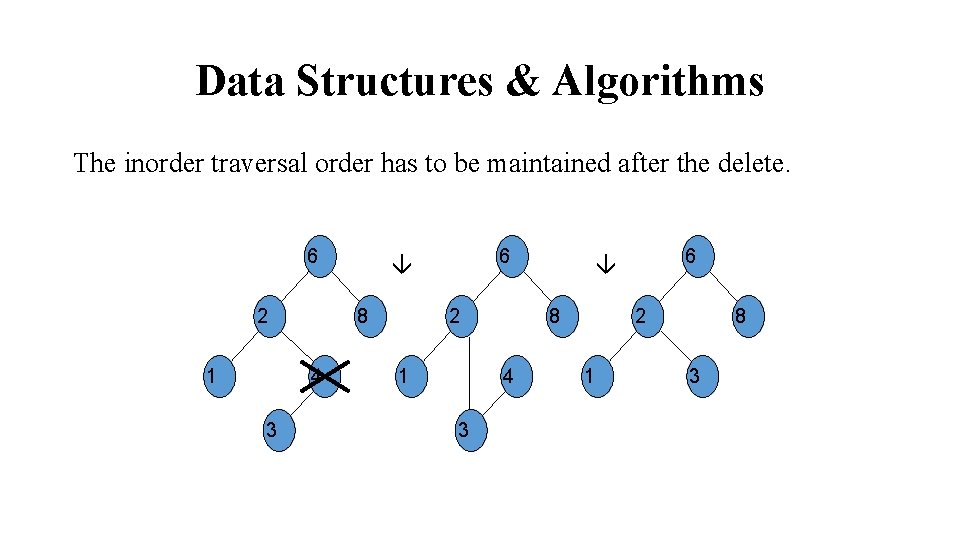
Data Structures & Algorithms Deleting a node in BST: As is common with many data structures, the hardest operation is deletion. Once we have found the node to be deleted, we need to consider several possibilities. If the node is a leaf, it can be deleted immediately. If the node has one child, the node can be deleted after its parent adjusts 6 a pointer to bypass the node and connect to inorder successor. 2 1 8 4 3

Data Structures & Algorithms The inorder traversal order has to be maintained after the delete. 6 2 1 8 4 3 6 2 1 8 3

Data Structures & Algorithms The complicated case is when the node to be deleted has both left and right subtrees. The strategy is to replace the data of this node with the smallest data of the right subtree and recursively delete that node.

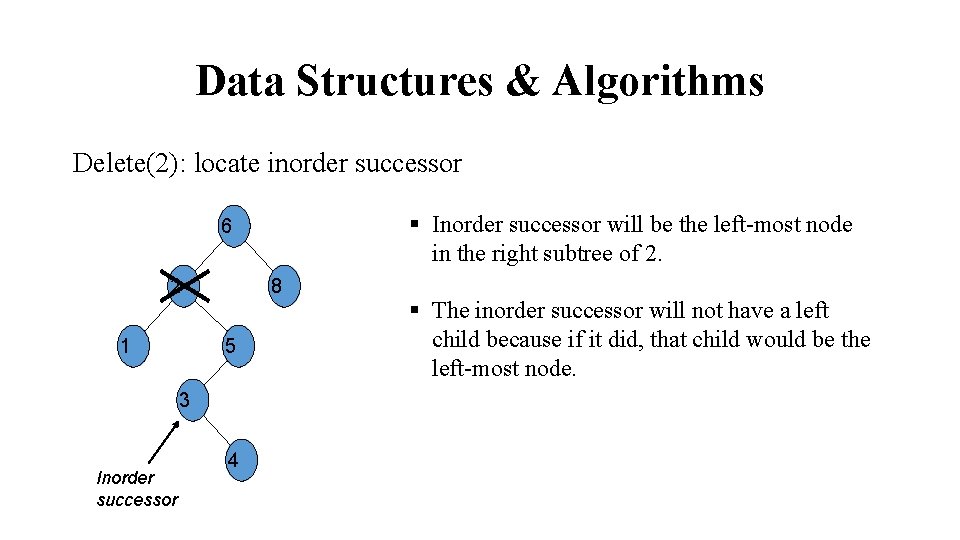
Data Structures & Algorithms Delete(2): locate inorder successor § Inorder successor will be the left-most node in the right subtree of 2. 6 2 1 8 5 3 Inorder successor 4 § The inorder successor will not have a left child because if it did, that child would be the left-most node.

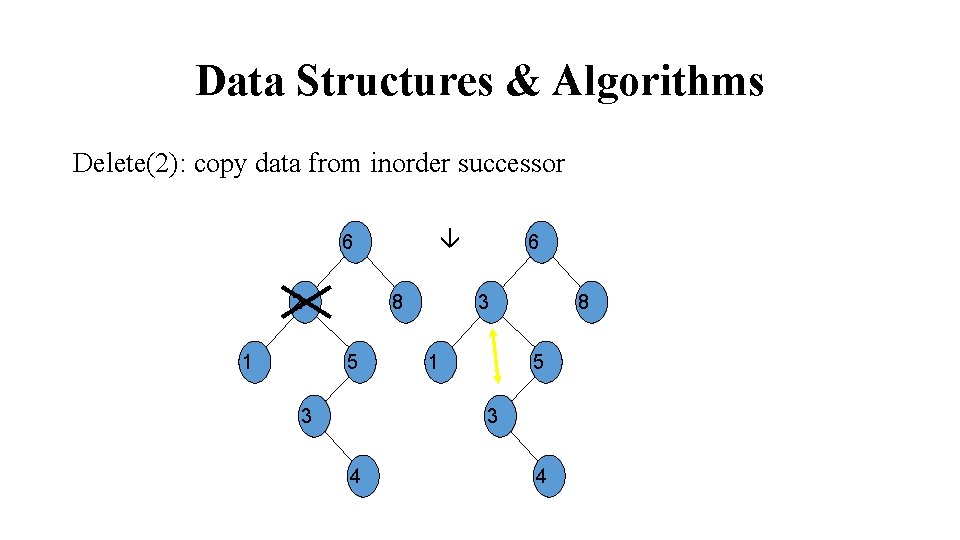
Data Structures & Algorithms Delete(2): copy data from inorder successor 6 2 1 8 5 3 6 3 1 8 5 3 4 4

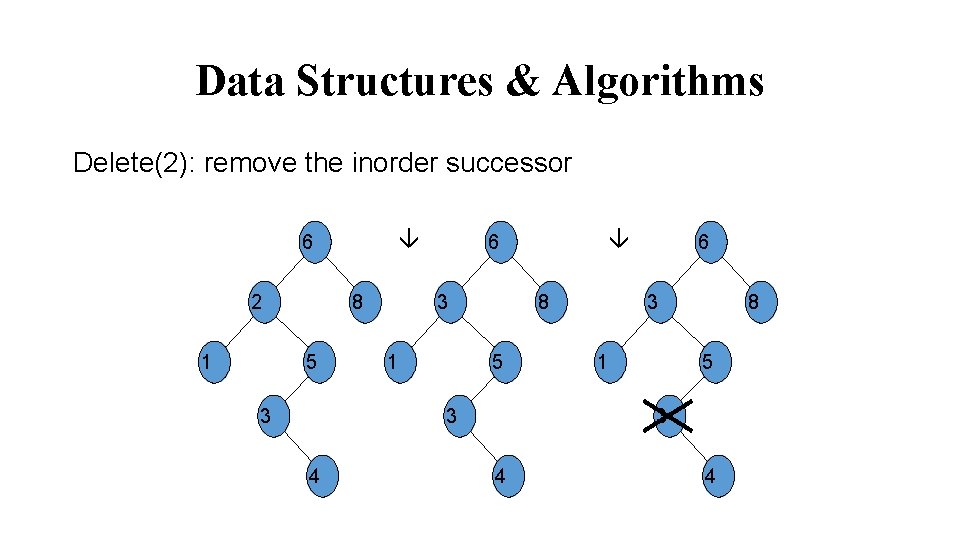
Data Structures & Algorithms Delete(2): remove the inorder successor 6 2 1 8 5 3 3 1 8 5 3 4 6 6 3 1 8 5 3 4 4

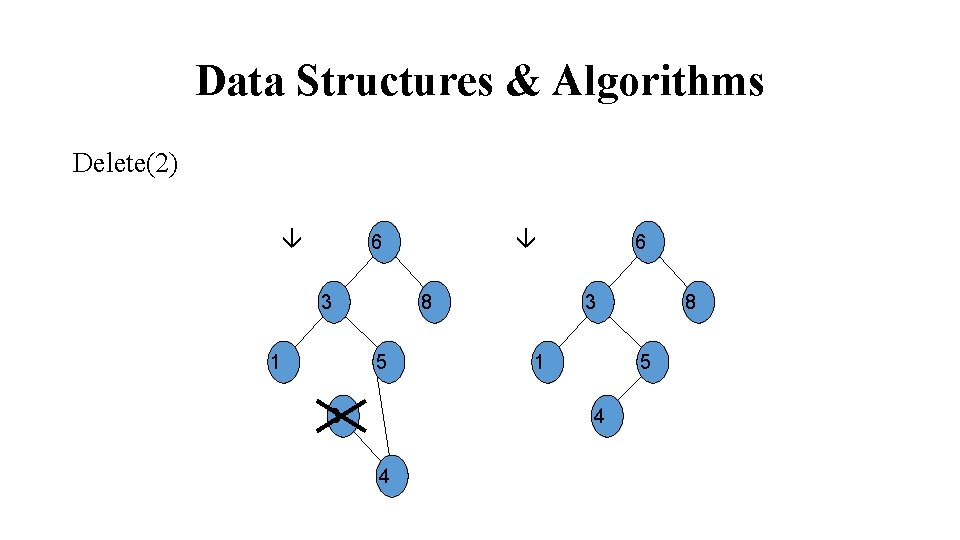
Data Structures & Algorithms Delete(2) 6 3 1 8 5 3 6 3 1 5 4 4 8

Data Structures & Algorithms ‘delete’ is C++ keyword. We will call our delete. Node routine remove. Here is the C++ code for remove.

Data Structures & Algorithms Tree. Node<int>* remove(Tree. Node<int>* tree, int info) { Tree. Node<int>* t; int cmp = info - *(tree->get. Info()); if( cmp < 0 ){ t = remove(tree->get. Left(), info); tree->set. Left( t ); } else if( cmp > 0 ){ t = remove(tree->get. Right(), info); tree->set. Right( t ); }

Data Structures & Algorithms //two children, replace with inorder successor else if(tree->get. Left() != NULL && tree->get. Right() != NULL ){ Tree. Node<int>* min. Node; min. Node = find. Min(tree->get. Right()); tree->set. Info( min. Node->get. Info() ); t = remove(tree->get. Right(), *(min. Node->get. Info())); tree->set. Right( t ); }

Data Structures & Algorithms else { // case 1 Tree. Node<int>* node. To. Delete = tree; if( tree->get. Left() == NULL ) //will handle 0 children tree = tree->get. Right(); else if( tree->get. Right() == NULL ) tree = tree->get. Left(); else tree = NULL; delete node. To. Delete; } return tree; }

Data Structures & Algorithms Tree. Node<int>* find. Min(Tree. Node<int>* tree) { if( tree == NULL ) return NULL; if( tree->get. Left() == NULL ) return tree; // this is it. return find. Min( tree->get. Left() ); }

Data Structures & Algorithms Let us design the Binary. Search. Tree class (factory). #ifndef _BINARY_SEARCH_TREE_H_ #define _BINARY_SEARCH_TREE_H_ #include <iostream. h> // For NULL // Binary node and forward declaration template <class EType> class Binary. Search. Tree;

Data Structures & Algorithms template <class EType> class Binary. Node { EType element; Binary. Node *left; Binary. Node *right; Binary. Node( const EType & the. Element, Binary. Node *lt, Binary. Node *rt ) : element( the. Element ), left( lt ), right( rt ) { } friend class Binary. Search. Tree<EType>; };

Data Structures & Algorithms template <class EType> class Binary. Search. Tree { public: Binary. Search. Tree( const EType& not. Found ); Binary. Search. Tree( const Binary. Search. Tree& rhs ); ~Binary. Search. Tree( ); const EType& find. Min( ) const; const EType& find. Max( ) const; const EType& find( const EType & x ) const; bool is. Empty( ) const; void print. Inorder( ) const;

Data Structures & Algorithms void insert( const EType& x ); void remove( const EType& x ); const Binary. Search. Tree & operator= ( const Binary. Search. Tree & rhs );

Data Structures & Algorithms private: Binary. Node<EType>* root; // ITEM_NOT_FOUND object used to signal failed finds const EType ITEM_NOT_FOUND; const EType& element. At( Binary. Node<EType>* t ); void insert(const EType& x, Binary. Node<EType>* & t); void remove(const EType& x, Binary. Node<EType>* & t); Binary. Node<EType>* find. Min(Binary. Node<EType>* t); Binary. Node<EType>* find. Max(Binary. Node<EType>* t); Binary. Node<EType>* find(const EType& x, Binary. Node<EType>* t ); void make. Empty(Binary. Node<EType>* & t); void print. Inorder(Binary. Node<EType>* t); };