Parallel vs Sequential Algorithms Design of efficient algorithms

Parallel vs Sequential Algorithms

Design of efficient algorithms A parallel computer is of little use unless efficient parallel algorithms are available. – The issue in designing parallel algorithms are very different from those in designing their sequential counterparts. – A significant amount of work is being done to develop efficient parallel algorithms for a variety of parallel architectures.

Processor Trends • Moore’s Law – performance doubles every 18 months • Parallelization within processors – pipelining – multiple pipelines

Why Parallel Computing • Practical: – Moore’s Law cannot hold forever – Problems must be solved immediately – Cost-effectiveness – Scalability • Theoretical: – challenging problems

Efficient and optimal parallel algorithms • A parallel algorithm is efficient iff – it is fast (e. g. polynomial time) and – the product of the parallel time and number of processors is close to the time of at the best know sequential algorithm T sequential T parallel N processors • A parallel algorithms is optimal iff this product is of the same order as the best known sequential time

The main open question • The basic parallel complexity class is NC. • NC is a class of problems computable in poly-logarithmic time (log c n, for a constant c) using a polynomial number of processors. • P is a class of problems computable sequentially in a polynomial time The main open question in parallel computations is NC = P ?

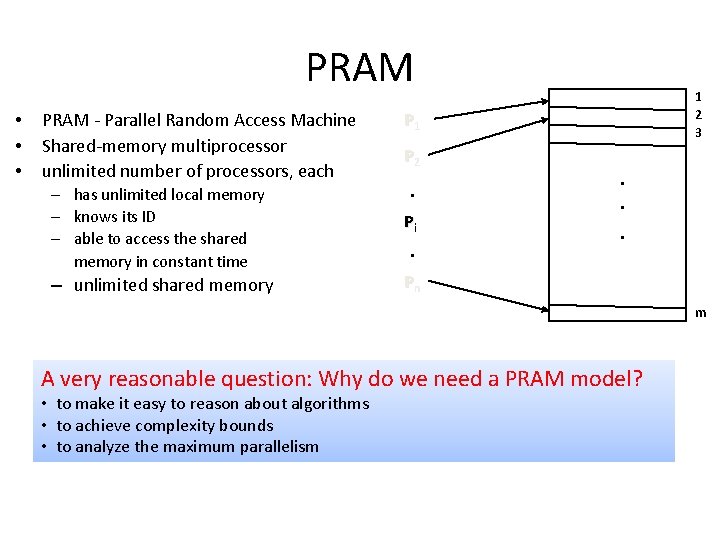
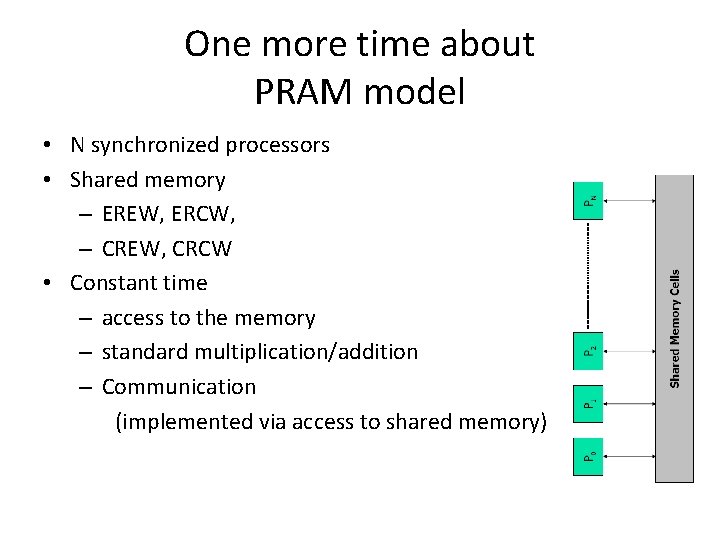
PRAM • • • PRAM - Parallel Random Access Machine Shared-memory multiprocessor unlimited number of processors, each – has unlimited local memory – knows its ID – able to access the shared memory in constant time – unlimited shared memory 1 2 3 P 1 P 2 . Pi . . Pn m A very reasonable question: Why do we need a PRAM model? • to make it easy to reason about algorithms • to achieve complexity bounds • to analyze the maximum parallelism

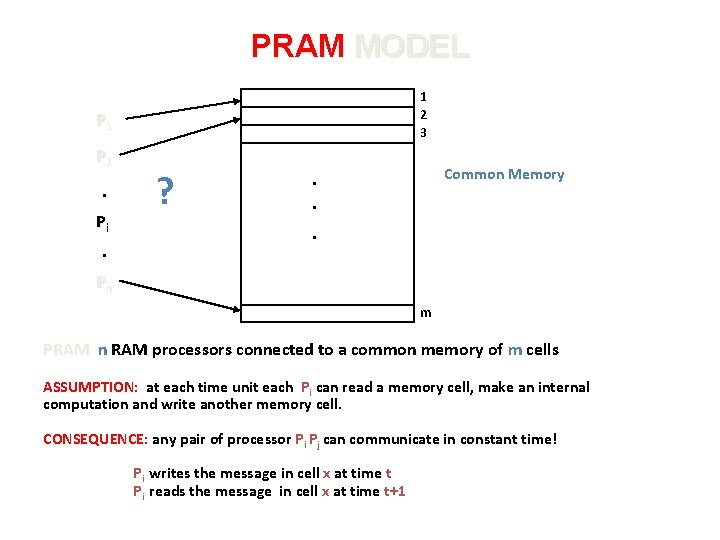
PRAM MODEL 1 2 3 P 1 P 2 . Pi . ? Common Memory . . . Pn m PRAM n RAM processors connected to a common memory of m cells ASSUMPTION: at each time unit each Pi can read a memory cell, make an internal computation and write another memory cell. CONSEQUENCE: any pair of processor Pi Pj can communicate in constant time! Pi writes the message in cell x at time t Pi reads the message in cell x at time t+1

Summary of assumptions for PRAM • Inputs/Outputs are placed in the shared memory (designated address) • Memory cell stores an arbitrarily large integer • Each instruction takes unit time • Instructions are synchronized across the processors PRAM Instruction Set • accumulator architecture – memory cell R 0 accumulates results • multiply/divide instructions take only constant operands – prevents generating exponentially large numbers in polynomial time

PRAM Complexity Measures • for each individual processor – time: number of instructions executed – space: number of memory cells accessed • PRAM machine – time: time taken by the longest running processor – hardware: maximum number of active processors

Two Technical Issues for PRAM • How processors are activated • How shared memory is accessed

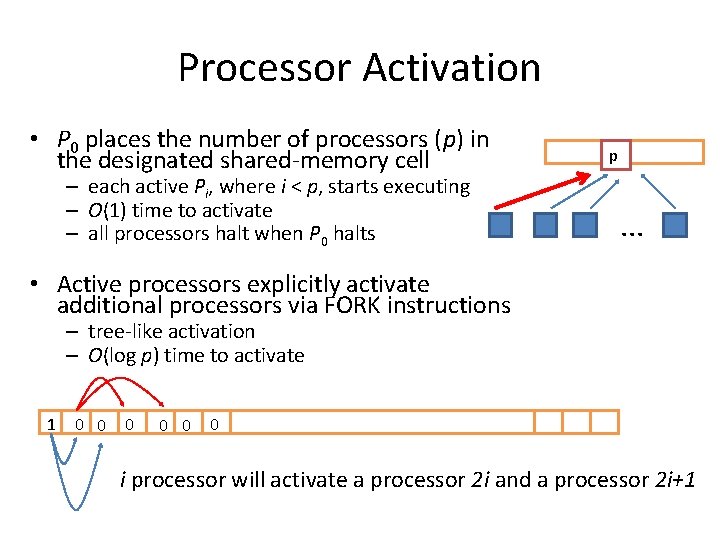
Processor Activation • P 0 places the number of processors (p) in the designated shared-memory cell – each active Pi, where i < p, starts executing – O(1) time to activate – all processors halt when P 0 halts p . . . • Active processors explicitly activate additional processors via FORK instructions – tree-like activation – O(log p) time to activate 1 0 0 0 i processor will activate a processor 2 i and a processor 2 i+1

PRAM • Too many interconnections gives problems with synchronization • However it is the best conceptual model for designing efficient parallel algorithms – due to simplicity and possibility of simulating efficiently PRAM algorithms on more realistic parallel architectures Basic parallel statement for all x in X do in parallel instruction (x) For each x PRAM will assign a processor which will execute instruction(x)

Shared-Memory Access Concurrent (C) means, many processors can do the operation simultaneously in the same memory Exclusive (E) not concurent • EREW (Exclusive Read Exclusive Write) • CREW (Concurrent Read Exclusive Write) – Many processors can read simultaneously the same location, but only one can attempt to write to a given location • ERCW (Exclusive Read Concurrent Write) • CRCW (Concurrent Read Concurrent Write) – Many processors can write/read at/from the same memory location

Concurrent Write (CW) • What value gets written finally? • Priority CW – processors have priority based on which write value is decided • Common CW – multiple processors can simultaneously write only if values are the same • Arbitrary/Random CW – any one of the values are randomly chosen

Example CRCW-PRAM • Initially – table A contains values 0 and 1 – output contains value 0 • The program computes the “Boolean OR” of A[1], A[2], A[3], A[4], A[5]

Example CREW-PRAM • Assume initially table A contains [0, 0, 0, 1] and we have the parallel program

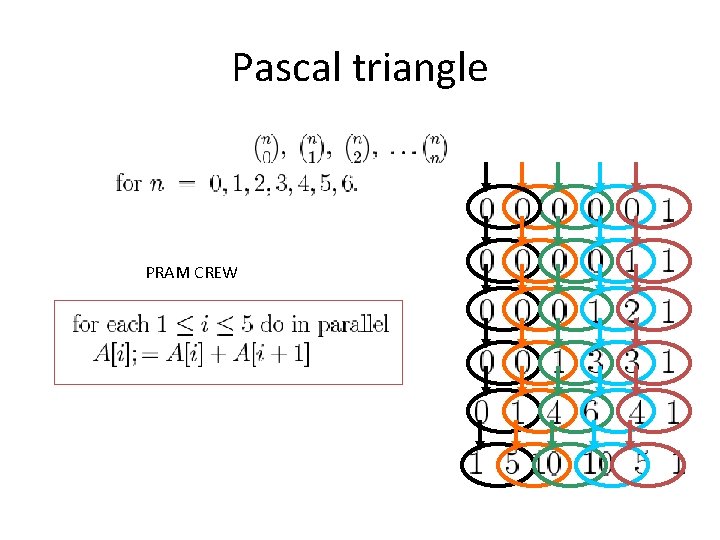
Pascal triangle PRAM CREW

Membership problem • p processors PRAM with n numbers (p ≤ n) • Does x exist within the n numbers? • P 0 contains x and finally P 0 has to know Algorithm step 1: Inform everyone what x is step 2: Every processor checks [n/p] numbers and sets a flag step 3: Check if any of the flags are set to 1

One more time about PRAM model • N synchronized processors • Shared memory – EREW, ERCW, – CREW, CRCW • Constant time – access to the memory – standard multiplication/addition – Communication (implemented via access to shared memory)

Two problems for PRAM Problem 1. Min of n numbers Problem 2. Computing a position of the first one in the sequence of 0’s and 1’s. How fast we can compute with many processor and how to reduce the number of processors?

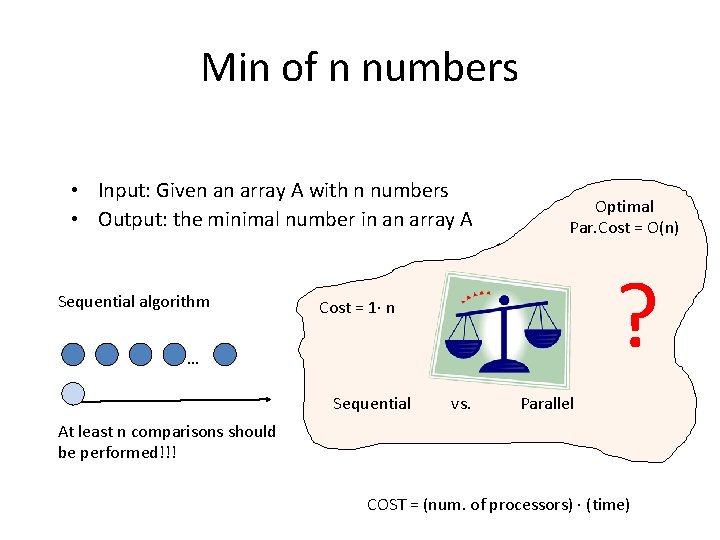
Min of n numbers • Input: Given an array A with n numbers • Output: the minimal number in an array A Sequential algorithm Optimal Par. Cost = O(n) ? Cost = 1 n … Sequential vs. Parallel At least n comparisons should be performed!!! COST = (num. of processors) (time)

Mission: Impossible … computing in a constant time • Archimedes: Give me a lever long enough and a place to stand I will move the earth • NOWDAYS…. Give me a parallel machine with enough processors and I will find the smallest number in any giant set in a constant time!

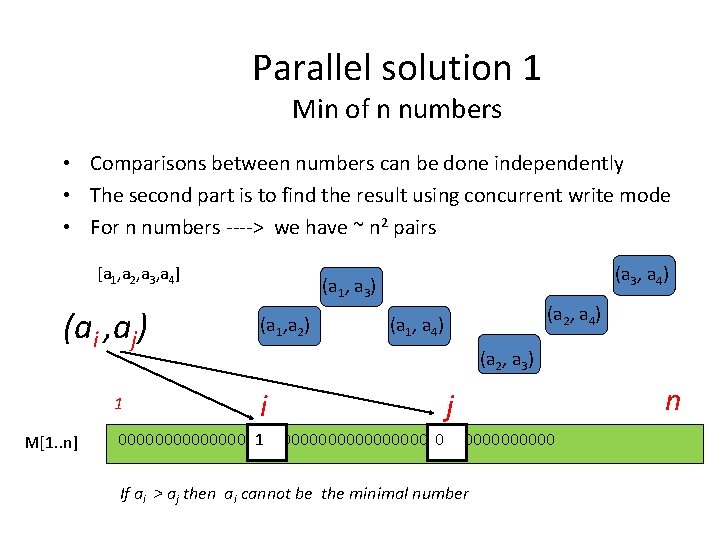
Parallel solution 1 Min of n numbers • Comparisons between numbers can be done independently • The second part is to find the result using concurrent write mode • For n numbers ----> we have ~ n 2 pairs [a 1, a 2, a 3, a 4] (ai , aj) 1 M[1. . n] (a 3, a 4) (a 1, a 3) (a 1, a 2) (a 2, a 4) (a 1, a 4) (a 2, a 3) i j 000000000000000000000000 1 0 If ai > aj then ai cannot be the minimal number n

The following program computes MIN of n numbers stored in the array C[1. . n] in O(1) time with n 2 processors. Algorithm A 1 for each 1 i n do in parallel M[i]: =0 for each 1 i, j n do in parallel if i j C[i] C[j] then M[j]: =1 for each 1 i n do in parallel if M[i]=0 then output: =i

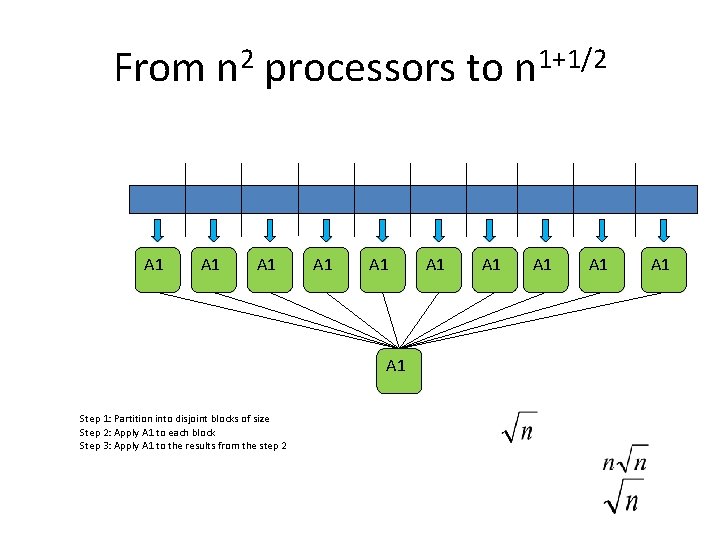
From n 2 processors to n 1+1/2 A 1 A 1 A 1 Step 1: Partition into disjoint blocks of size Step 2: Apply A 1 to each block Step 3: Apply A 1 to the results from the step 2 A 1 A 1 A 1

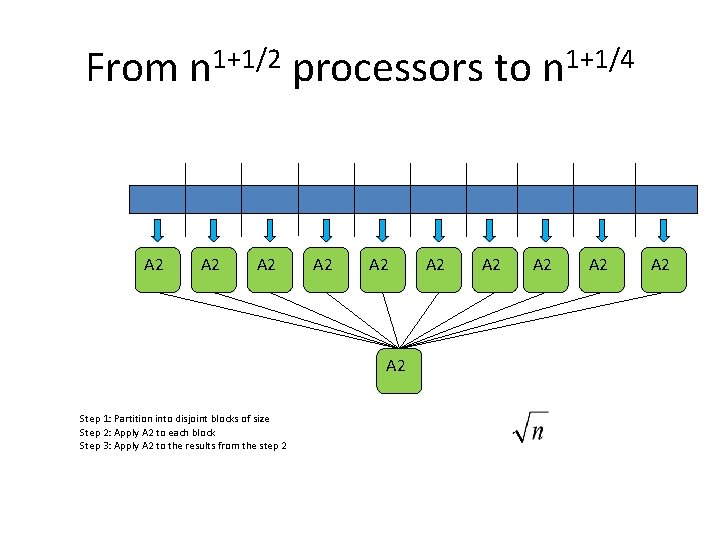
From n 1+1/2 processors to n 1+1/4 A 2 A 2 A 2 Step 1: Partition into disjoint blocks of size Step 2: Apply A 2 to each block Step 3: Apply A 2 to the results from the step 2 A 2 A 2 A 2

n 2 -> n 1+1/4 -> n 1+1/8 -> n 1+1/16 ->… -> n 1+1/k ~ n 1 • Assume that we have an algorithm Ak working in O(1) time with processors Algorithm Ak+1 1. Let =1/2 2. Partition the input array C of size n into disjoint blocks of size n each 3. Apply in parallel algorithm Ak to each of these blocks 4. Apply algorithm Ak to the array C’ consisting of n/ n minima in the blocks.

Complexity • We can compute minimum of n numbers using CRCW PRAM model in O(log n) with n processors by applying a strategy of partitioning the input Par. Cost = n log n

Mission: Impossible (Part 2) Computing a position of the first one in the sequence of 0’s and 1’s in a constant time. 0000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000 0000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000010000000001 00000000000000000000000000000000000000000000000000000000100000000000000000000001000 000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000010000001111 00000000000000000000000000000000000000000000000000000000 1111000000000000100000000000000000000000000000000000000000000000000000000100000000000000000000000000000000100000000000000000000000000000000000000000000000000000000 0001000000000000000000000000000000000001000000000000000000000000000000001000 00000000000000000000000000000000000000000000000000000000111111111111111000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000001000000111111110000000000 0001000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000000100000000000000000000010000000000000000000000100000000000000000000100000011111111000000000000100000000000000000000000000000000000000000000000000000000 00101000 00000001 01101000 00010100

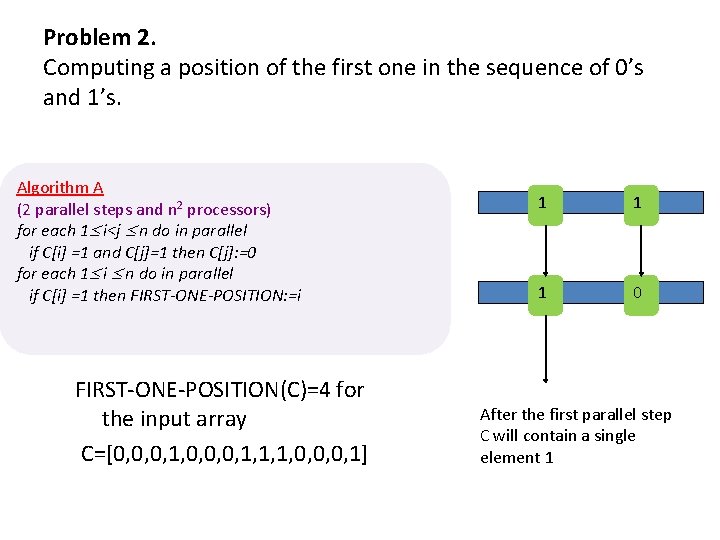
Problem 2. Computing a position of the first one in the sequence of 0’s and 1’s. Algorithm A (2 parallel steps and n 2 processors) for each 1 i<j n do in parallel if C[i] =1 and C[j]=1 then C[j]: =0 for each 1 i n do in parallel if C[i] =1 then FIRST-ONE-POSITION: =i FIRST-ONE-POSITION(C)=4 for the input array C=[0, 0, 0, 1, 1, 1, 0, 0, 0, 1] 1 1 1 0 After the first parallel step C will contain a single element 1

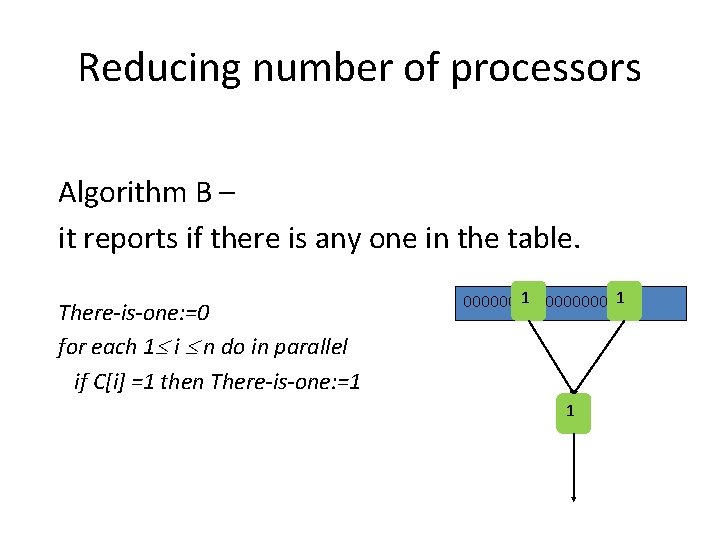
Reducing number of processors Algorithm B – it reports if there is any one in the table. There-is-one: =0 for each 1 i n do in parallel if C[i] =1 then There-is-one: =1 1 1 000000000 1

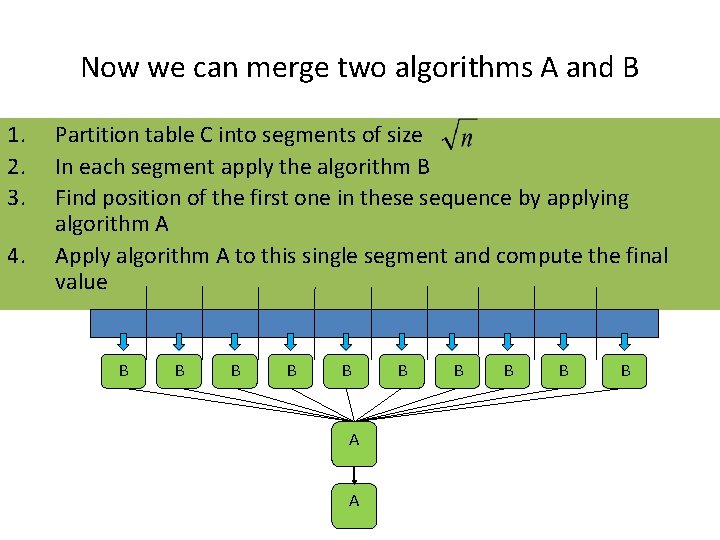
Now we can merge two algorithms A and B 1. 2. 3. 4. Partition table C into segments of size In each segment apply the algorithm B Find position of the first one in these sequence by applying algorithm A Apply algorithm A to this single segment and compute the final value B B B A A B B B

Complexity • We apply an algorithm A twice and each time to the array of length which need only ( )2 = n processors • The time is O(1) and number of processors is n.

Tractable and intractable problems for parallel computers

P (complexity) • In computational complexity theory, P is the complexity class containing decision problems which can be solved by a deterministic Turing machine using a polynomial amount of computation time, or polynomial time. • P is known to contain many natural problems, including linear programming, calculating the greatest common divisor, and finding a maximum matching. • In 2002, it was shown that the problem of determining if a number is prime is in P.

P-complete class • In complexity theory, the complexity class P-complete is a set of decision problems and is useful in the analysis of which problems can be efficiently solved on parallel computers. • A decision problem is in P-complete if it is complete for P, meaning that it is in P, and that every problem in P can be reduced to it in polylogarithmic time on a parallel computer with a polynomial number of processors. • In other words, a problem A is in P-complete if, for each problem B in P, there are constants c and k such that B can be reduced to A in time O((log n)c) using O(nk) parallel processors.

Motivation • The class P, typically taken to consist of all the "tractable" problems for a sequential computer, contains the class NC, which consists of those problems which can be efficiently solved on a parallel computer. This is because parallel computers can be simulated on a sequential machine. • It is not known whether NC=P. In other words, it is not known whethere any tractable problems that are inherently sequential. • Just as it is widely suspected that P does not equal NP, so it is widely suspected that NC does not equal P.

P-complete problems • The most basic P-complete problem is this: Given a Turing machine, an input for that machine, and a number T (written in unary), does that machine halt on that input within the first T steps? • It is clear that this problem is P-complete: if we can parallelize a general simulation of a sequential computer, then we will be able to parallelize any program that runs on that computer. • If this problem is in NC, then so is every other problem in P.

• This problem illustrates a common trick in theory of Pcompleteness. We aren't really interested in whether a problem can be solved quickly on a parallel machine. • We're just interested in whether a parallel machine solves it much more quickly than a sequential machine. Therefore, we have to reword the problem so that the sequential version is in P. That is why this problem required T to be written in unary. • If a number T is written as a binary number (a string of n ones and zeros, where n=log(T)), then the obvious sequential algorithm can take time 2 n. On the other hand, if T is written as a unary number (a string of n ones, where n=T), then it only takes time n. By writing T in unary rather than binary, we have reduced the obvious sequential algorithm from exponential time to linear time. That puts the sequential problem in P. Then, it will be in NC if and only if it is parallelizable.

P-complete problems • Many other problems have been proved to be Pcomplete, and therefore are widely believed to be inherently sequential. These include the following problems, either as given, or in a decision-problem form: • In order to prove that a given problem is P-complete, one typically tries to reduce a known P-complete problem to the given one, using an efficient parallel algorithm.

Examples of P-complete problems • Circuit Value Problem (CVP) - Given a circuit, the inputs to the circuit, and one gate in the circuit, calculate the output of that gate • Game of Life - Given an initial configuration of Conway's Game of Life, a particular cell, and a time T (in unary), is that cell alive after T steps? • Depth First Search Ordering - Given a graph with fixed ordered adjacency lists, and nodes u and v, is vertex u visited before vertex v in a depth-first search?

Problems not known to be P-complete • Some problems are not known to be either NP-complete or P. These problems (e. g. factoring) are suspected to be difficult. • Similarly there are problems that are not known to be either P -complete or NC, but are thought to be difficult to parallelize. • Examples include the decision problem forms of finding the greatest common divisor of two binary numbers, and determining what answer the extended Euclidean algorithm would return when given two binary numbers.

Conclusion • Just as the class P can be thought of as the tractable problems, so NC can be thought of as the problems that can be efficiently solved on a parallel computer. • NC is a subset of P because parallel computers can be simulated by sequential ones. • It is unknown whether NC = P, but most researchers suspect this to be false, meaning that there are some tractable problems which are probably "inherently sequential" and cannot significantly be sped up by using parallelism • The class P-Complete can be thought of as "probably not parallelizable" or "probably inherently sequential".