Distributed Algorithms by Nancy A Lynch Chapter 8

“Distributed Algorithms” by Nancy A. Lynch Chapter 8 Asynchronous System Model by Mikhail Nesterenko

Outline • • I/O automaton definition examples of I/O automata execution operations on I/O automata – composition – hiding fairness properties and proof methods – invariants – trace properties – compositional reasoning – hierarchical proofs complexity randomization

I/O Automaton Signature • Iinput/Output automaton A is a state machine that models a component of a distributed system – the transitions associated with named actions acts(A) • main part of I/O automaton is its signature: sig(A) - a description of actions, actions can be • input - in(sig(A)) or just in(A) • output - out(A) • internal actions int(A) • sets of actions are disjoint • input and output actions are external actions, external signature (external interface) extsig(A) contains external actions only

I/O Automaton Parts • • signature sig(A) (possibly) infinite set of states(A) non-empty subset of initial states start(A) a state transition relation trans(A) states(A) acts(A) states(A) – there must be a transition for every state and every input actions (the automata are input-enabled) – a member of trans(A) is transition, an action is enabled at a state if a the corresponding transition is in trans(A) – state is quiescent if only input actions are enabled • task partition tasks(A) - a separation of internal and output actions into subset to model different objectives of A

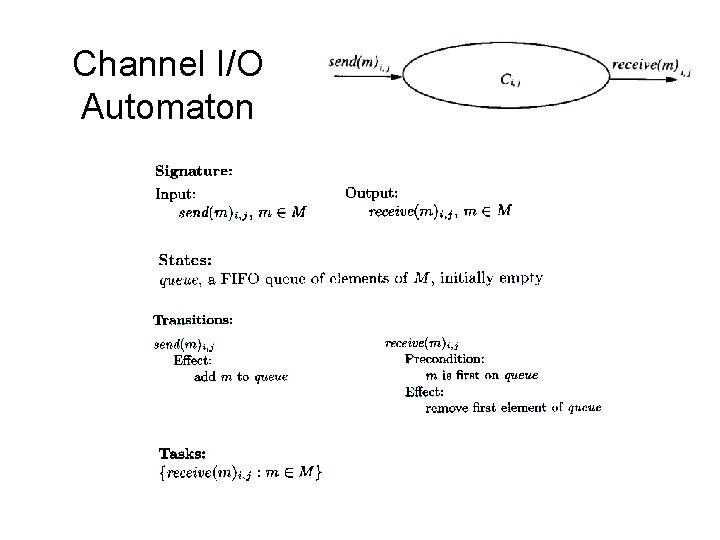
Channel I/O Automaton

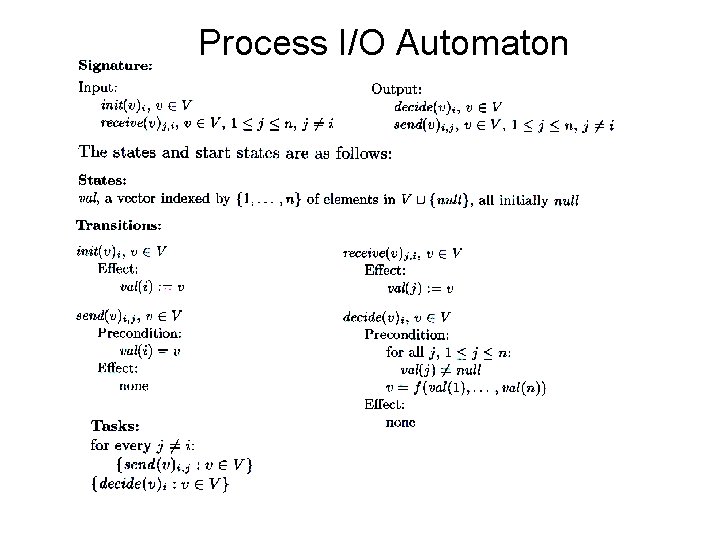
Process I/O Automaton

Execution • finite (or infinite) sequence s 0, p 1, s 1, p 2, …, pr, sr is execution fragment if each (pk, sk, pk+1) is a transition of A • execution is an execution fragment that starts in an initial state • a state is reachable if it is a final state of a finite execution of A • example: channel automata executions (assuming messages are {1, 2} • a trace of an execution a of A (denoted trace(a) or trace(A)) is a projection of the execution on external actions • traces(A) - a set of traces of A

Compatible Components • allows constructing of complex system out of individual components • informally - components are joined, individual component’s actions are executed, when action p is executed by one component, each component with p (the same action) executes it • a collection of components is compatible if their signatures are as follows – internal actions of one component are not observable by any other (i. e. the internal actions are disjoint) – only one component controls output (output sets of any two components are disjoint) – each action is contained in finitely many components

Composition • given a collection of compatible signatures {Si}i I the composition S=P I Si of signatures is defined as follows • a composition A=P I Ai of automata is • A B is a composition of components A and B

Exposed outputs • Observe that even though some of the inputs (the ones that have corresponding output) of the components are removed from the composition, all outputs of components are outputs of composition • this is done to allow convenient composition • example component A has output action p while B and C have p as input action – that is p is “broadcast” to both B and C • if p is not exposed then (A B) C as well as is not possible

Hidden outputs • there is an operation that “hides” the output actions of components by reclassifying them as internal actions (they are not used in further communication and do not appear in traces) • if for some signature S, an some subset of output actions S out(S) hiding operation hide. S(S) is defined as a new signature S’ such hat: – in(S’)=in(S), out(S’)=out(S)-S, and int(S’)=int(S) S – hiding of output actions for an automaton involves hiding of these actions for the automaton’s signature

Example Composition • composition of process and channel automata assuming N=3 • the transitions are as follows • example trace assuming N=2 and the function f is addition

Composition Theorems • given an execution a, a|A is the projection (removal) of all the transitions that are not in A

Fairness • interesting executions - each components “take fair turns” at performing transitions • recall - each automaton is partitioned into tasks • informally fairness allows each task to perform one of its actions infinitely often • formally, let C be set of tasks and a - an execution fragment, a is fair if – a is finite and C is not enabled in the final state – a is infinite and it contains either • infinitely many transitions from C or • infinitely many states where all actions of C are disabled • fairexec(A) - a set of fair executions of A • trace is fair if it is a trace of fair execution • fairtrace(A) a set of fair traces of A

Fairness Examples • example: channel automata executions (assuming messages are {1, 2} fair not fair

Fairness Examples: Clock Automaton executions • tick, – fair • tick, tick – not fair (no fair finite executions for Clock) • tick, request, tick, clock(4), tick, … - fair • tick, request, tick, … - not fair

Fairness Theorem

Invariants • Invariant (assertion) for A is a property that is true in all reachable states of A • usually proved by induction on the number of steps in the execution • can be done by providing a sequence of invariants and proceeding from one to the next – note: “we” tend to think of an invariant as an assertion (predicate) on a state which is less generic than Lynch’s definition

Trace Properties • reasoning of the properties of an automaton is done in terms of its traces • formally a trace property P is – a signature sig(P) containing no internal actions – a set traces(P) of (finite or infinite) sequences of actions of sig(P) • A satisfies trace property P means either of the two – extsig(A)=sig(P) and traces(A) traces(P) – extsig(A)=sig(P) and fairtraces(A) traces(P) in either case the satisfaction intuitively means that the behavior that can be produced by A is permitted by P; the reverse (completion) is not required

Automata and Trace Properties

Safety Properties • P is a trace safety property if – traces(P) is not empty – traces(P) is prefix closed – every prefix of a trace in traces(P) is also in traces(P) • intuitively – if nothing “bad” happens in a trace, nothing bad happens in a prefix of the trace – traces(P) is limit-closed – given an infinite sequence of finite sequences b 1, b 2, … such that each consequent finite sequence is contains the preceding one as a prefix, the limit of this infinite sequence is also in traces(P) • intuitively – if nothing “bad” happens in any of the prefixes then nothing bad happens in the trace itself

Liveness Properties, Theorems • P is liveness property if every finite sequence from acts(P) has some extensions in traces(P) – intuitively – an arbitrary prefix can be made “live” and extended to conform to a liveness property Theorem 8. 8 if a property is both a liveness and safety property then it contains all possible sequences of actions Theorem 8. 9 every property is an intersection of a liveness and safety property

Proof Techniques • compositional reasoning – proves properties of the composed automaton on the basis of the properties of the components and composition techniques • hierarchical proofs – describe the system in an abstract model and, prove it conforms to a property then move (refine) the abstraction while preserving the property

Indistinguishable Executions, Randomization • if a and a’ are two executions of a composed systems of automata each containing automaton A, a and a’ are indistinguishable to A provides a|A=a’|A • probabilistic I/O automaton – notion of transition is modified: instead of (s, p, s’), it is (s, p, P) where P is a probability distribution over some set of states