Analysis of Algorithms Aaron Tan Analysis of Algorithms

Analysis of Algorithms Aaron Tan Analysis of Algorithms http: //www. comp. nus. edu. sg/~tantc/cs 1101. html

Introduction to Analysis of Algorithms n After you have read and studied this chapter, you should be able to § Know what is analysis of algorithms (complexity analysis) § Know the definition and uses of big-O notation § How to analyse the running time of an algorithm Analysis of Algorithms 2

Introduction (1/2) n Two aspects on writing efficient codes: ¨ Programming n n Implementation of algorithms Practitioner’s viewpoint ¨ Asymptotic n n techniques analysis (“big-O” notation, etc. ) Analysis and design of algorithms Theoretician’s viewpoint Asymptotic analysis keeps the student’s head in the clouds, while attention to implementation details keeps his feet on the grounds. + Analysis of Algorithms 3

Introduction (2/2) n Programming techniques versus Algorithm design: int f 1 (int n) { int a, sum=0; for (a=1; a<=n; a++) sum += a; return sum; } + Analysis of Algorithms 4

Sum of Two Elements (1/5) n Given this problem: ¨A sorted list of integers list and a value is given. Write a program to find the indices of (any) two distinct elements in the list whose sum is equal to the given value. ¨ Example: list: 2, 3, 8, 12, 15, 19, 22, 24 sum: 23 answer: elements 8 (at subscript 2) and 15 (at subscript 4) Analysis of Algorithms 5

Sum of Two Elements (2/5) n Algorithm A: list: 2, 3, 8, 12, 15, 19, 22, 24 sum: 23 answer: elements 8 (at subscript 2) and 15 (at subscript 4) n = size of list for x from 0 to n – 2 for y from x + 1 to n – 1 if ((list[x] + list[y]) == sum) then found! (answers are x and y) Analysis of Algorithms 6

Sum of Two Elements (3/5) n Code for algorithm A: import java. util. *; class Sum. Of. Two. A { public static void main(String[] args) { Scanner scanner = new Scanner(System. in); int[] list = { 2, 3, 8, 12, 15, 19, 22, 24 }; int n = list. length; System. out. print("Enter sum: "); int sum = scanner. next. Int(); boolean found = false; for (int x = 0; x < n-1 && !found; x++) for (int y = x+1; y < n && !found; y++) if (list[x] + list[y] == sum) { System. out. println("Indices at " + x + " and " + y); found = true; } } } Analysis of Algorithms 7

Sum of Two Elements (4/5) n n Algorithm A used nested loop and scans some elements many times. Algorithm B: can you use a single loop to examine each element at most once? ¨ If this can be done, it will be more efficient than Algorithm A. Analysis of Algorithms 8

Sum of Two Elements (5/5) n Code for algorithm B: + Analysis of Algorithms 9

The Race 100 metres ahead Who will reach the finishing line first? Analysis of Algorithms 10

Complexity Analysis (1/2) n Complexity analysis: to measure and predict the behavior (running time, storage space) of an algorithm. n We will focus on running time here. n Inexact, but provides a good basis for comparisons. n We want to have a good judgment on how an algorithm will perform if the problem size gets very big. Analysis of Algorithms 11

Complexity Analysis (2/2) n Problem size is defined based on the problem on hand. n Examples of problem size: ¨ Number ¨ Length of elements in an array (for sorting problems). of the strings in an anagram problem. ¨ Number of discs in the Tower of Hanoi problem. ¨ Number of cities in the Traveling Salesman Problem (TSP). Analysis of Algorithms 12

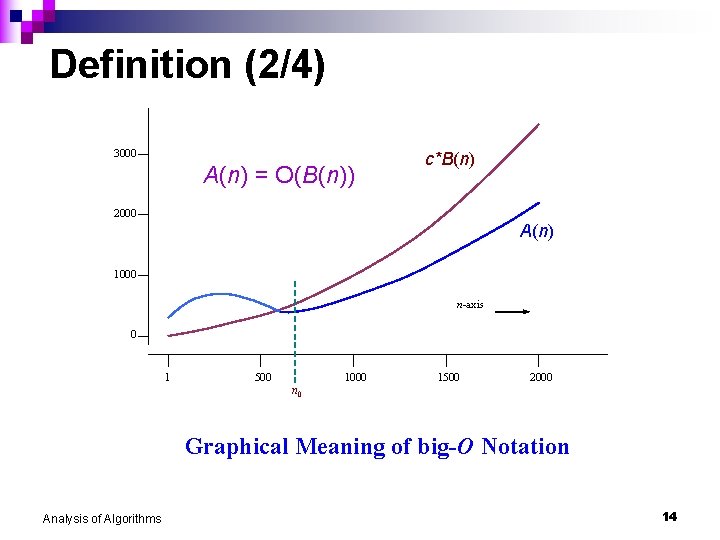
Definition (1/4) n Assume problem size is n and T(n) is the running time. n Upper bound – Big-O notation Definition: T(n) = O(f(n)) if there are constants c and n 0 such that T(n) c*f(n) when n n 0 n We read the equal sign = as “is a member of” ( ), because O(f(n)) is a set of functions. n We may also say that T(n) is bounded above by f(n). Analysis of Algorithms 13

Definition (2/4) 3000 A(n) = O(B(n)) c*B(n) K * g(n) f(n) 2000 A(n) 1000 n-axis 0 1 500 1000 1500 2000 n 0 Graphical Meaning of big-O Notation Analysis of Algorithms 14

Definition (3/4) n The functions’ relative rates of growth are compared. n For instance, compare f(n) = n 2 with g(n) = 1000 n. n ¨ Although at some points f(n) is smaller than g(n), f(n) actually grows at a faster rate than g(n). (Hence, an algorithm with running time complexity of f(n) is slower than another with running time complexity of g(n) in this example. ) ¨ Hence, g(n) = O(f(n)). The definition says that eventually there is some point n 0 past which c*f(n) is always larger or equal to g(n). ¨ Here, we can make c = 1 and n 0 = 1000. Analysis of Algorithms 15

Definition (4/4) n Besides the big-O (upper bound) analysis, there are the Omega (lower bound) analysis, the Theta (tight bounds) analysis, and others. Analysis of Algorithms 16

Exercises (1/4) n f(n) = 1 + 2 + 3 + … + n Show that f(n) = O(n 2) Proof: 1 + 2 + 3 + … + n = n(n+1)/2 = n 2/2 + n/2 n 2/2 + n 2/2 = n 2 n The above is the running time of basic sorting algorithms such as bubblesort, insertion sort, selection sort. Analysis of Algorithms 17

Exercises (2/4) n f(n) = 17 + n/3 Show that f(n) = O(n) Proof: 17 + n/3 3 n = O(n) n f(n) = n 4 + n 2 + 20 n + 100 Show that f(n) = O(n 4) Proof: n 4 + n 2 + 20 n + 100 4 n 4 = O(n 4) n From the two examples above, it can be seen that an expression is dominated by the term of the highest degree. Analysis of Algorithms 18

Exercises (3/4) n Tower of Hanoi Algorithm: Tower(n, source, temp, dest) { if (n > 0) { tower(n-1, source, dest, temp); move disc from source to dest; tower(n-1, temp, source, dest); } } Let T(n) = number of move to solve a tower of n discs. Analysis of Algorithms 19

Exercises (4/4) n Tower of Hanoi (cont. ) Let T(n) = number of move to solve a tower of n discs. Prove that T(n) = 2 n – 1. T(0) = 0 T(n) = T(n – 1) + 1 + T(n – 1) = 2 T(n – 1) + 1 = 2 (2 n– 1 – 1) + 1 = 2 2 n– 1 – 2 +1 = 2 n – 1 Hence T(n) = O(2 n) Analysis of Algorithms 20

Some Common Series 1 + 2 + 4 + 8 + 16 + …+ 2 n 1+2+3+4+5…+n 12 + 2 2 + 3 2 + 4 2 + 5 2 … + n 2 Analysis of Algorithms 21

The Conversation n Boss: Your program is too slow! Rewrite it! n You: But why? All we need to do is to buy faster computer! Is this really the solution? Analysis of Algorithms 22

Complexity Classes (1/4) n There are some common complexity classes. ¨ In analysis of algorithm, log refers to log 2, or sometimes written simply as lg. Notation Name O(1) Constant. O(log n) Logarithmic. O(n) Linear. O(n log n) Linearithmic, loglinear, quasilinear or supralinear. O(n 2) Quadratic. O(nc), c > 1 Polynomial, sometimes called algebraic. Examples: O(n 2), O(n 3), O(n 4). O(cn) Exponential, sometimes called geometric. Examples: O(2 n), O(3 n). O(n!) Factorial, sometimes called combinatorial. Analysis of Algorithms n is problem size. 23

Complexity Classes (2/4) n Algorithms of polynomial running times are desirable. Table 1. Running Times for Different Complexity Classes Analysis of Algorithms 24

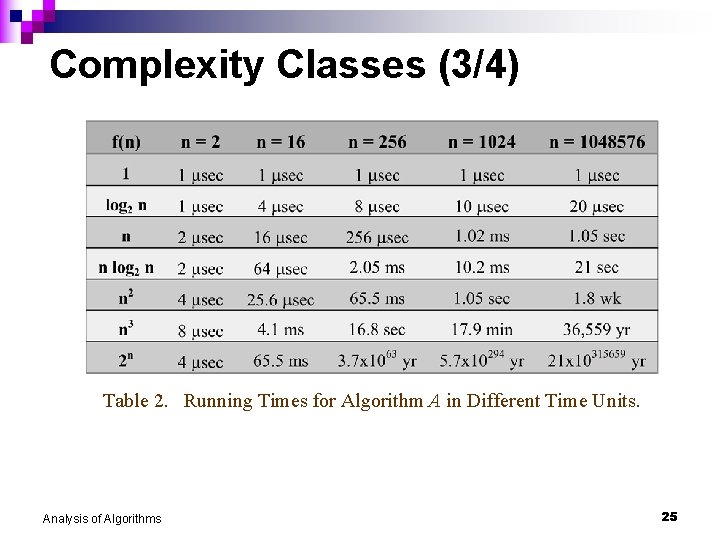
Complexity Classes (3/4) Table 2. Running Times for Algorithm A in Different Time Units. Analysis of Algorithms 25

Complexity Classes (4/4) Table 3. Size of Largest Problem that Algorithm A can solve if solution is computed in time <= T at 1 micro-sec per step. Analysis of Algorithms 26

Analysing Simple Codes (1/4) n Some rules. n Basic operations are those that can be computed in O(1) or constant time. ¨ Examples are assignment statements, comparison statements, and simple arithmetic operations. Analysis of Algorithms 27

Analysing Simple Codes (2/4) n Code fragment 1: temp = x; x = y; y = temp; Running time: 3 statements = O(1) n Code fragment 2: p = list. size(); for (int i = 0; i < p; ++i) { list[i] += 3; } Running time: 1 + p statements = O(p) Analysis of Algorithms 28

Analysing Simple Codes (3/4) n Code fragment 3: if (x < y) { a = 1; b = 2; c = 3; } else { a = 2; b = 4; c = 8; d = 13; e = 51; } Running time: max{3, 5} statements = 5 = O(1) In code fragments 2 and 3, we consider only assignment statements as our basic operations. Even if we include the loop test operation (i < p) and update operation (++i) in fragment 2, and the if test operation (x < y) in fragment 3, it will not affect the final result in big. O notation, since they are each of constant time. Analysis of Algorithms 29

Analysing Simple Codes (4/4) n Code fragment 4: sum = 0. 0; for (int k = 0; k < n; ++k) sum += array[k]; avg = sum/n; Running time: 1 + n + 1 statements = n + 2 = O(n) n Code fragment 5: for (int i = 0; i < n; i++) for (int j = 0; j < i; ++j) sum += matrix[i][j]; Running time: 0 + 1 + 2 + … + (n-1) = n(n-1)/2 = O(n 2) Analysis of Algorithms 30

General Rules (1/3) n Rule 1: Loops ¨ The running time of a loop is at most the running time of the statements inside the loop times the number of iterations. for (. . . ) { …; …; …; } n iterations m statements n m statements Example: if m = 3, then running time is 3 n or O(n). Analysis of Algorithms 31

General Rules (2/3) n Rule 2: Nested loops ¨ Analyse these inside out. The total running time of a statement inside a group of nested loops is the running time of the statement multiplied by the product of the sizes of all the loops. for (…) { for (. . . ) { …; …; …; } } Analysis of Algorithms k iterations O(kn) O(n) 32

General Rules (3/3) n Rule 3: Selection statements ¨ For the fragment if (condition) S 1; else S 2; the running time of an if-else statement is never more than the running time of the condition test plus the larger of the running times of S 1 and S 2. if (…) { …; } else { …; } Analysis of Algorithms m statements max{m, n} n statements 33

Worst-case Analysis n We may analyze an algorithm/code based on the bestcase, average-case and worst-case scenarios. n Average-case and worst-case analysis are usually better indicators of performance than best-case analysis. n Worst-case is usually easier to determine than averagecase. Analysis of Algorithms 34

Running Time of Some Known Algorithms n The following are worst-case running time of some known algorithms on arrays. The problem size, n, is the number of elements in the array. ¨ Sequential search (linear search) in an array: O(n). ¨ Binary search in a sorted array: O(lg n). ¨ Simple sorts (bubblesort, selection sort, insertion sort): O(n 2). ¨ Mergesort: O(n lg n). Analysis of Algorithms 35

Sequential Search vs Binary Search (1/2) n Sequential/linear search: Start from first element, visit each element to see if it matches the search item. public static int linear. Search(int[] list, int search. Value) { for (int i = 0; i < list. length; i++) { if (list[i] == search. Value) return i; } return -1; } Analysis of Algorithms 36

Sequential Search vs Binary Search (2/2) n Binary search: Works for sorted array. ¨ Examine middle element, and eliminate half of the array. ¨ public static int binary. Search(int[] list, int search. Value) { int left = 0; int right = list. length - 1; int mid; while (left <= right) { mid = (left + right)/2; if (list[mid] == search. Value) return mid; else if (list[mid] < search. Value) left = mid + 1; else right = mid - 1; } return -1; } Analysis of Algorithms 37

Analysis of Sequential Search n Assume: An array with n elements. ¨ Basic operation is the comparison operation. ¨ n Best-case: ¨ n Worst-case: ¨ n When the key is found at the first element. Running time: O(1). When the key is found at the last element, or when the key is not found. Running time: O(n). Average case: ¨ Assuming that the chance of every element that matches the key is equal, then on average the key is found after n/2 compare operations. Running time: O(n). Analysis of Algorithms 38

Analysis of Binary Search n Assume: An array with n elements. ¨ Basic operation is the comparison operation. ¨ n Best-case: ¨ n When the key is found at the middle element. Running time: O(1). Worst-case: Running time: O(lg n). Why? ¨ If you start with the value n, how many times can you half it until it becomes 1? ¨ Examples: Starting with 8, it takes 3 halving to get it to 1; starting with 32, it takes 5 halving; starting with 1024, it takes 10 halving. ¨ Analysis of Algorithms 39

Analysis of Sort Algorithms n For comparison-based sorting algorithms, the basic operations used in analysis is The number of comparisons, or ¨ The number of swaps (exchanges). ¨ n Worst-case analysis: All the three basic sorts – selection sort, bubble sort, and insertion sort – have worst-case running time of O(n 2), where n is the array size. ¨ What is the worst-case scenario for bubble sort? For selection sort? For insertion sort? ¨ Analysis of Algorithms 40

Maximum Subsequence Sum (1/6) n Given this problem: ¨ Given (possibly negative) integers a 0, a 1, a 2, …, an-1, find the maximum value of (For convenience, the maximum subsequence sum is 0 if all the integers are negative. ) ¨ Example: ¨ list: -2, 11, -4, 13, -5, -2 answer: 20 (a 1 through a 3). ¨ Many algorithms to solve this problem. Analysis of Algorithms 41

Maximum Subsequence Sum (2/6) n Algorithm 1 public static int max. Subseq. Sum(int[] list) { int this. Sum, max. Sum; max. Sum = 0; for (int i = 0; i < list. length; i++) for (int j = 0; j < list. length; j++) { this. Sum = 0; for (int k = i; k <= j; k++) this. Sum += list[k]; // count this line if (this. Sum > max. Sum) max. Sum = this. Sum; } return max. Sum; } Analysis of Algorithms 42

Maximum Subsequence Sum (3/6) n Algorithm 1: Analysis How many times is line this. Sum += list[k]; executed? Analysis of Algorithms 43

Maximum Subsequence Sum (4/6) n Algorithm 2 + Analysis of Algorithms 44

Maximum Subsequence Sum (5/6) n Algorithm 2: Analysis Algorithm 2 avoids the cubic running time O(n 3) by removing the inner-most for-k loop in algorithm 1. New running-time complexity is O(n 2). Analysis of Algorithms 45

Maximum Subsequence Sum (6/6) n Algorithm 3 + Analysis of Algorithms 46

End of file 47