CSE 246 Computer Arithmetic Algorithms and Hardware Design

CSE 246: Computer Arithmetic Algorithms and Hardware Design Lecture 6. 1 Multiplication Arithmetic Instructor: Prof. Chung-Kuan Cheng CSE 246

Topics: n n CSE 246 Karatsuba’s Method (1962) Toom’s Method (1963) Modular Method FFT 2

Karatsuba’s Method U=2 n. U 1+U 0, V=2 n. V 1+V 0 o UV= 22 n. U 1 V 1+2 n(U 1 V 0+U 0 V 1)+U 0 V 0 = (22 n+2 n)U 1 V 1+2 n(U 1 -U 0)(V 0 -V 1)+(2 n+1)U 0 V 0 o T(2 n)<= 3 T(n)+cn T(2 k)<=c(3 k-2 k) T(n)=T(2 lgn)<=c(3 lgn-2 lgn)<3 cnlg 3=1. 585 CSE 246 3

Toom’s Method U=2 rn. Ur+…+2 n. U 1+U 0 o V=2 rn. Vr+…+2 n. V 1+V 0 o U(x)= xr. Ur+…+x. U 1+U 0 o V(x)= xr. Vr+…+x. V 1+V 0 o U(x)V(x)=W(x)= x 2 r. W 2 r+…+x. W 1+W 0 Set 2 r+1 equations: W(0)=U(0)V(0) W(1)=U(1)V(1) W(2 r)=U(2 r)V(2 r) o CSE 246 4

Toom’s Method o o T((r+1)n)<= (2 r+1)T(n)+cn T(n)<=cnlogr+1(2 r+1)<cn 1+logr+12 Theorem: Given e> 0, there exists a multiplication algorithm such that the number of elementary operation T(n) needed to multiply two n-bit numbers satisfies for some constant c(e) independent of n T(n)<c(e)n 1+e CSE 246 5

Toom’s Method o o o U=(4, 13, 2)16, V=(9, 2, 5)16 U(x)=4 x 2+13 x+2, V=9 x 2+2 x+5 W(x)=U(x)V(x) W(0)=10, W(1)=304, W(2)=1980 W(3)=7084, W(4)=18526 W(x)= x 2 r. W 2 r+…+x. W 1+W 0 CSE 246 6

Toom’s Method W(x)= x 2 r. W 2 r+…+x. W 1+W 0 o Rewrite W(x)= a 2 rx 2 r+…+a 1 x 1+a 0 where xk=x(x-1)…(x-k+1) W(x+1)-W(x)= 2 ra 2 rx 2 r-1+(2 r-1)a 2 r-1 x 2 r-2…+a 1 (W(x+2)-W(x+1))-(W(x+1)-W(x))= 2 r(2 r-1)a 2 rx 2 r-2+(2 r-1)(2 r-2)a 2 r-1 x 2 r-3…+2 a 2 o CSE 246 7

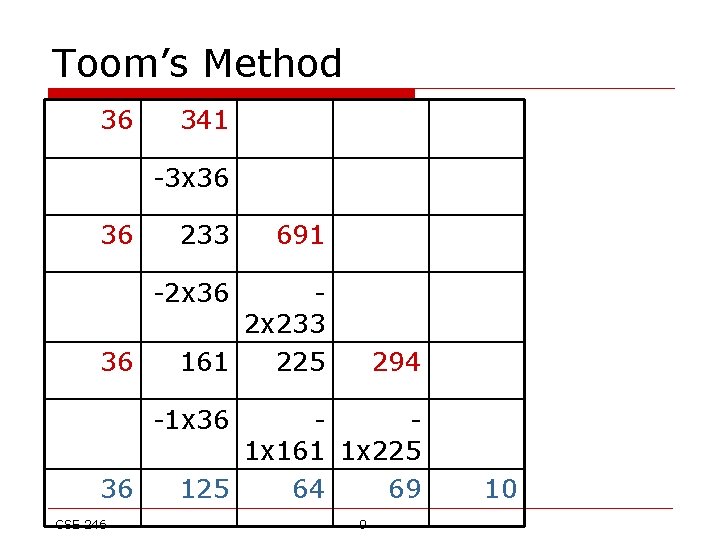
Toom’s Method W(*)=10, 304, 1980, 7084, 18526 o W’(*)=294, 1676, 5104, 11442 o W’’(*)=1382, 3428, 6338 o W’’(*)/2= 691, 1714, 3169 o W’’’(*)/2= 1023, 1455 o W’’’(*)/6= 341, 485 o W’’’’(*)/6= 144 o W’’’’(*)/24= 36 o W(x)= 36 x 4+341 x 3+691 x 2+294 x 1+10 =(((36(x-3)+341)(x-2)+691)(x-1)+294)x+10 = 36 x 4+125 x 3+64 x 2+69 x+10 o CSE 246 8

Toom’s Method 36 341 -3 x 36 36 233 691 -2 x 36 36 2 x 233 161 225 294 -1 x 36 36 CSE 246 1 x 161 1 x 225 125 64 69 9 10

Toom and Cook’s Method o Theorem: There is a constant c such that the execution time of Toom and Cook’s method is less than cn 23. 5 sqrt(lgn) cycles CSE 246 10

Modular Method (Schonhage) Recursive formula: q 0=1, qk+1=3 qk-1 o Thus, we have qk=1/2(3 k+1) o Relatively prime pi 6 qk-1, 6 qk+2, 6 qk+3, 6 qk+5, 6 qk+7 o Set six moduli mi=2 pi-1 o CSE 246 11

Modular Method o o Given U and V, Find W=Ux. V Compute ui=Umodmi vi=Vmodmi Compute wi=uixvimodmi Recover W T(n)=O(nlog 36)=O(n 1. 631) CSE 246 12

FFT Given U(t)=(u 0, u 1, …u. K-1), V(t)=(v 0, v 1, …v. K-1) Find P(t)=(p 0, p 1, …, p. K-1), where pt=sum(i+j=t mod. K) uivj o o o Set w=exp(2 pi/K), i. e. w. K=1 us= sum(0<=t<K) wstut vs= sum(0<=t<K) wstvt U(s)V(s)=(u 0 v 0, u 1 v 1, …, u. K-1 v. K-1) P(s)=U(s)V(s), ps=usvs ps= sum(0<=t<K) wstpt CSE 246 13

FFT o o o K>= 2 n-1, un=un+1=…=u. K-1=0 vn=vn+1=…=v. K-1=0 pt=sum(i+j=t mod. K)uivj =utv 0+ut-1 v 1+…+u 0 vt CSE 246 14

FFT (K=2 k , t=(tk-1, …, t 0)) o o Set A 0(tk-1, …, t 0)=ut , i. e. A 0(t)=ut Set A 1(sk-1, tk-2, …, t 0)= A 0(0, tk-2, …, t 0)+w 2 k-1 sk-1 A 0(1, tk-2, …, t 0) Set A 2(sk-1, sk-2, tk-3, …, t 0)= A 1(sk-1, 0, tk-3, …, t 0)+ k-2(s 2 k-2 sk-1)2 A (s w 1 k-1, 1, tk-3, …, t 0) Set Ak(sk-1, sk-2, sk-3, …, s 0)= Ak-1(sk-1, …, s 1, 0)+ w(s 0 s 1…sk-1)2 Ak-1(sk-1, …, s 1, 1) CSE 246 15

FFT (K=2 k , t=(tk-1, …, t 0)) o o o o Replace tk-1 with sk-1 k-1 s 2 k-1 sk-1 determines w Replace tk-2 with sk-2 k-2(s 2 k-2 sk-1)2 sk-1, sk-2 determines w Replace t 0 with s 0 sk-1, sk-2, …, s 0 determines w(s 0 s 1…sk-1)2 Binary s=(s 0, s 1, …, sk-1)2 CSE 246 16

FFT (K=2 k , t=(tk-1, …, t 0)) By induction, we have Aj(sk-1, …, sk-j, tk-j-1, …, t 0)= sum(tk-1, …, tk-j)w 2 k-j (sk-j, …, sk-1)2 (tk-1, …, tk-j)2 ut Ak(sk-1, …, s 0)= sum(tk-1, …, t 0) w(s 0, …, sk-1)2(tk-1, …, t 0)2 ut =us CSE 246 17

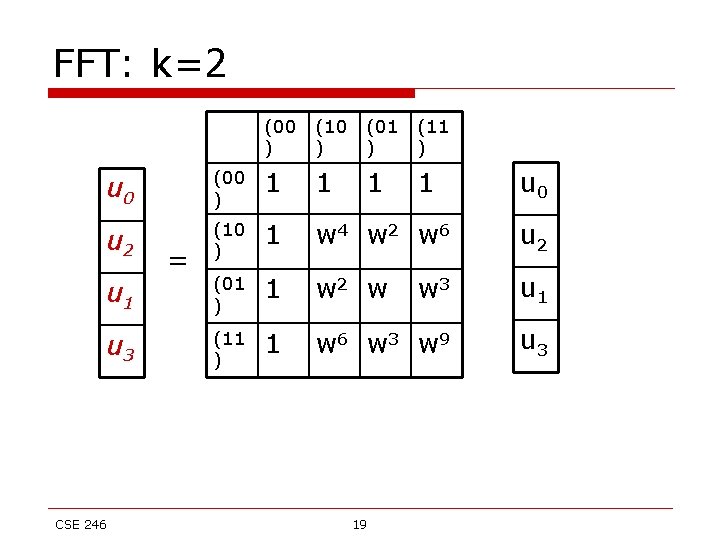
FFT: k=2 (00 ) (01 ) (10 ) (11 ) 1 u 0 (00 ) 1 1 1 u 1 (01 ) 1 w w 2 w 3 u 1 u 2 (10 ) 1 w 2 w 4 w 6 u 2 u 3 (11 ) 1 w 3 w 6 w 9 u 3 CSE 246 = 18

FFT: k=2 (00 ) (10 ) (01 ) (11 ) 1 1 u 0 (00 ) 1 1 u 2 (10 ) 1 w 4 w 2 w 6 u 2 u 1 (01 ) 1 w 2 w w 3 u 1 u 3 (11 ) 1 w 6 w 3 w 9 u 3 CSE 246 = 19

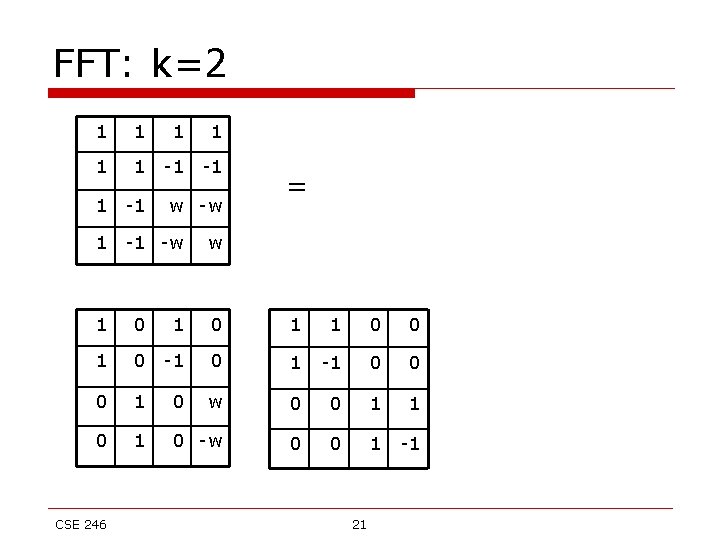
FFT: k=2 (00) (10) (01) (11) u 0 (00) 1 1 u 0 u 2 (10) 1 1 -1 -1 u 2 u 1 (01) 1 -1 w -w u 1 u 3 (11) 1 -1 -w w u 3 CSE 246 = 20

FFT: k=2 1 1 1 -1 -1 -w w -w = w 1 0 1 1 0 0 1 0 -1 0 1 -1 0 0 0 1 0 w 0 0 1 1 0 -w 0 0 1 -1 CSE 246 21

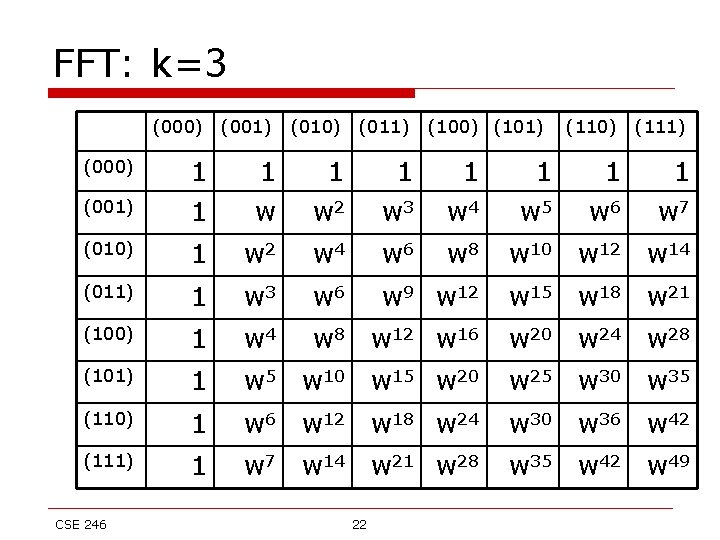
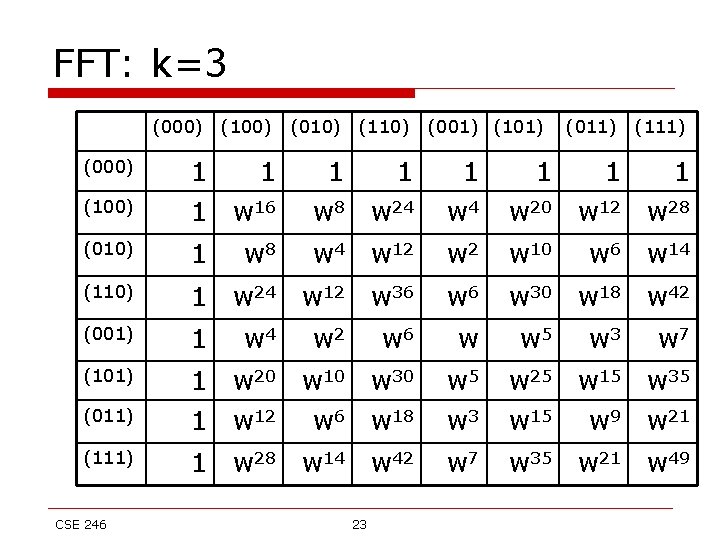
FFT: k=3 (000) (001) (010) (011) (000) 1 1 1 (001) 1 w w 2 w 3 w 4 (010) 1 w 2 w 4 w 6 w 8 w 10 w 12 w 14 (011) 1 w 3 w 6 w 9 w 12 w 15 w 18 w 21 (100) 1 w 4 w 8 w 12 w 16 w 20 w 24 w 28 (101) 1 w 5 w 10 w 15 w 20 w 25 w 30 w 35 (110) 1 w 6 w 12 w 18 w 24 w 30 w 36 w 42 (111) 1 w 7 w 14 w 21 w 28 w 35 w 42 w 49 CSE 246 22 (100) (101) (110) (111) 1 1 1 w 5 w 6 w 7

FFT: k=3 (000) (100) (010) (110) (000) 1 1 1 (100) 1 w 16 w 8 w 24 w 20 w 12 w 28 (010) 1 w 8 w 4 w 12 w 10 (110) 1 w 24 w 12 w 36 w 30 w 18 w 42 (001) 1 (101) w 2 1 (111) 1 1 w 6 w 14 w 1 w 20 w 10 w 30 w 5 w 25 w 15 w 35 (011) 1 w 12 w 6 w 18 w 3 w 15 (111) 1 w 28 w 14 w 42 w 7 w 35 w 21 w 49 23 w 5 (011) w 6 CSE 246 w 4 (001) (101) w 3 w 7 w 9 w 21

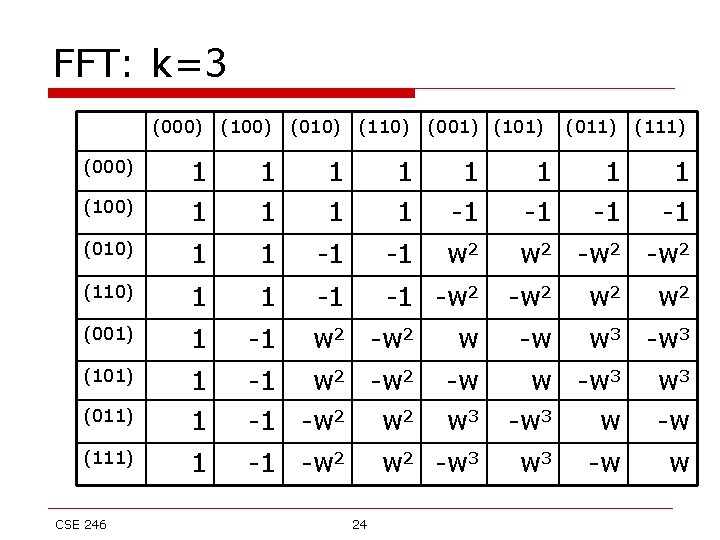
FFT: k=3 (000) (100) (010) (110) (000) 1 1 1 (100) 1 1 (010) 1 1 -1 -1 (110) 1 1 -1 -1 -w 2 (001) 1 -1 w 2 -w 2 w (101) 1 -1 w 2 -w (011) 1 -1 -w 2 w 3 -w 3 w -w (111) 1 -1 -w 2 -w 3 -w w CSE 246 24 (001) (101) (011) (111) 1 1 1 -1 -1 w 2 -w 2 -w w 2 w 3 -w 3 w 3

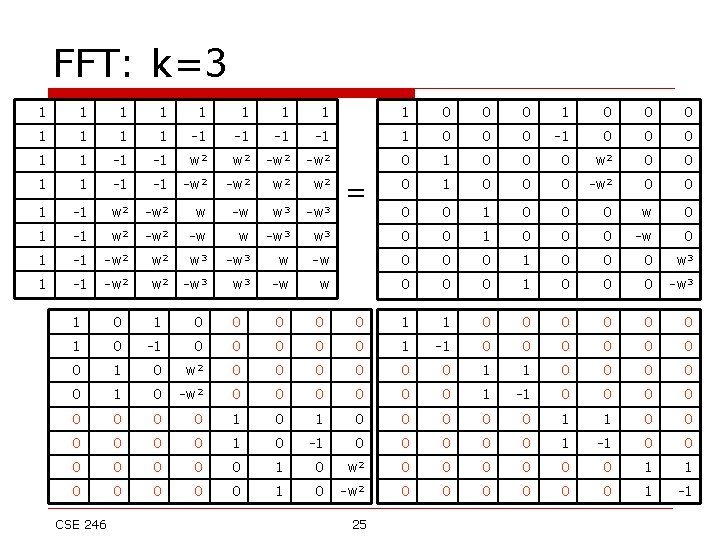
FFT: k=3 1 1 1 1 1 0 0 0 1 1 -1 -1 1 0 0 0 -1 0 0 0 1 1 -1 -1 w 2 -w 2 0 1 0 0 0 w 2 0 0 1 1 -1 -1 -w 2 w 2 0 1 0 0 0 -w 2 0 0 1 -1 w 2 -w 2 w -w w 3 -w 3 0 0 1 0 0 0 w 0 1 -1 w 2 -w w -w 3 0 0 1 0 0 0 -w 0 1 -1 -w 2 w 3 -w 3 w -w 0 0 0 1 0 0 0 w 3 1 -1 -w 2 -w 3 -w w 0 0 0 1 0 0 0 -w 3 1 0 0 0 1 0 -1 0 0 0 1 -1 0 0 0 0 1 0 w 2 0 0 0 1 1 0 0 0 1 0 -w 2 0 0 0 1 -1 0 0 0 0 1 1 0 0 0 1 0 -1 0 0 0 1 -1 0 0 0 0 1 0 w 2 0 0 0 1 1 0 0 0 1 0 -w 2 0 0 0 1 -1 CSE 246 = 25

FFT o o k-1 2 s us=u 0+u 1 s+u 2 2 k-1 k-2 2 2 us=u 0+u 2 s +…+u 2 k-2 s +u 1 s+u 3 s 3+…+u 2 k-1 s 2 k-1 us= Fe(s 2) + s. Fd(s 2) k-2 2 Fe(s )=u 0+u 2 s +…+u 2 k-2 s k-1 2 2 2 Fd(s )=u 1+u 3 s +…+u 2 k-1 s us= Fee(s 4)+s 2 Fed(s 4) + s[Fde(s 4) +s 2 Fdd(s 4)] CSE 246 s 2+…+u 26

FFT o o us=u 0+u 1 s+u 2 s 2+…+u 2 k-1 s 2 k-1 us= Fee(s 4)+s 2 Fed(s 4) + s[Fde(s 4) +s 2 Fdd(s 4)] us= Feee(s 8)+ s 4 Feed(s 8) + s 2[Fede(s 8)+ s 4 Fedd(s 8)] + s{[Fdee(s 8)+s 4 Fded(s 8)] +s 2[Fdde(s 8)+ s 4 Fddd(s 8)]} k-1 k 2 2 Fx…x(s )= Fx…xe(s ) + s Fx…xd(s ) CSE 246 27

FFT o o o us=u 0+u 1 s+u 2 s 2+u 3 s 3+u 4 s 4+u 5 s 5+u 6 s 6+u 7 s 7 us= Fe(s 2) + s. Fd(s 2) Fe(s 2)=u 0+u 2 s 2+u 4 s 4+u 6 s 6 Fd(s 2)=u 1+u 3 s 2+u 5 s 4+u 7 s 6 Fe(s 2)=Fee(s 4) + s 2 Fed(s 4) Fee(s 4)=u 0+u 4 s 4, Fed(s 4)=u 2+u 6 s 6 Fd(s 2)=Fde(s 4) + s 2 Fdd(s 4) Fde(s 4)=u 1+u 5 s 4, Fdd(s 4)=u 3+u 7 s 4 Fx(s=w 0)=Fx(s=w 4), Fx(s=w 2)=Fx(s=w 6), Fx(s=w)=Fx(s=w 5), Fx(s=w 3)=Fx(s=w 7) x=e, d (s 0, s 1, s 2)=(-, 0, 0), (-, 0, 1), (-, 1, 0), (-, 1, 1) Fxx(s=w 0)=Fxx(s=w 2)=Fxx(s=w 4)=Fxx(s=w 6), Fxx(s=w)=Fxx(s=w 3)=Fxx(s=w 5)=Fxx(s=w 7), xx=ee, ed, de, dd, (s 0, s 1, s 2)=(-, -, 0), (-, -, 1) CSE 246 28

FFT (Inversion) o ur== sum(0<=s<K)wrsus = sum(0<=s, t<K)wrswstut = sum(0<=t<K)utsum(0<=s<K)ws(t+r) =Ku(-r)mod. K sum(0<=s<K)wsj=K if jmod. K=0, 0 otherwise. CSE 246 29

FFT o o 2 n<=2 k g< 4 n, K=2 k Precision m= 6 k Let M= time of m-bit multiplication Total time to multiply n-bit numbers O(n)+O(Mnk/g) CSE 246 30