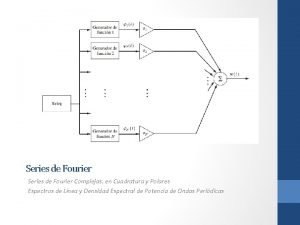
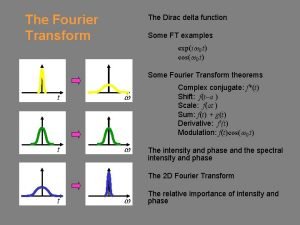
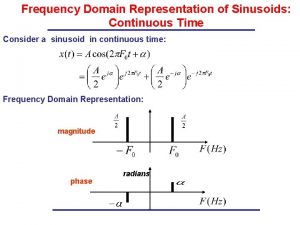
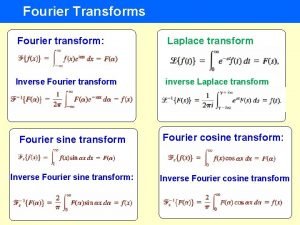
594 Chapter 11 Orthogonal Functions and Fourier Series



![597 11. 1. 2 定義 (1) inner product on an interval [a, b] (f 597 11. 1. 2 定義 (1) inner product on an interval [a, b] (f](https://slidetodoc.com/presentation_image_h2/dc4894f5d5e108523f879525faf3cf26/image-4.jpg)

![599 (2) orthogonal on an interval [a, b] (f 1, f 2 為 real 599 (2) orthogonal on an interval [a, b] (f 1, f 2 為 real](https://slidetodoc.com/presentation_image_h2/dc4894f5d5e108523f879525faf3cf26/image-6.jpg)





![605 (8) complete 若在 interval [a, b] 之間,任何一個 function f(x) 都可以表 示成 0(x), 1(x), 605 (8) complete 若在 interval [a, b] 之間,任何一個 function f(x) 都可以表 示成 0(x), 1(x),](https://slidetodoc.com/presentation_image_h2/dc4894f5d5e108523f879525faf3cf26/image-12.jpg)






















































































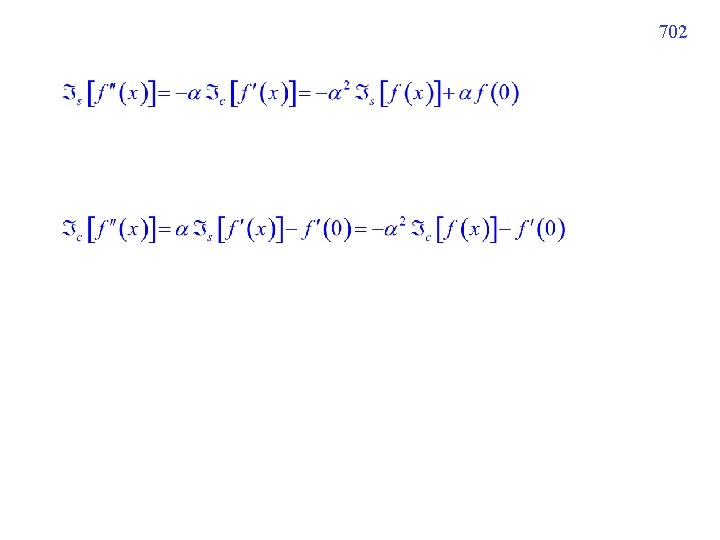














- Slides: 123

594 Chapter 11 Orthogonal Functions and Fourier Series 複習: linear algebra 關於 orthogonal (正交) basis 的介紹 在 linear algebra 當中 (1) inner product (2) orthogonal (3) 若 f 1, f 2, …. , f. N 為 complete orthogonal set, where

例如 在只有三個 entry 的情形下 是一組 complete orthogonal set f 3 f 2 f 1 問題:在 continuous 當中該如何定義 orthogonal? 595

596 Section 11. 1 Orthogonal Functions 11. 1. 1 綱要:熟悉幾個重要定義 (1) inner product (pp. 597) (7) normalize (pp. 604) (2) orthogonal (pp. 599) (8) complete (pp. 605) (3) orthogonal set (pp. 600) (9) orthogonal series expansion (pp. 606) (4) square norm (pp. 602) (10) generalized Fourier series (pp. 606) (5) norm (pp. 602) (11) weight function (pp. 608) With weighting functions, many definition s are changed. 學習方式:(1) 可以多和 linear algebra 當中的定義多比較 (6) orthonormal set (pp. 602) (2) 複習三角函式的公式 (see pp. 611 -612)
![597 11 1 2 定義 1 inner product on an interval a b f 597 11. 1. 2 定義 (1) inner product on an interval [a, b] (f](https://slidetodoc.com/presentation_image_h2/dc4894f5d5e108523f879525faf3cf26/image-4.jpg)
597 11. 1. 2 定義 (1) inner product on an interval [a, b] (f 1, f 2 為 real 時) 比較: discrete case 補充:more standard definition for inner product with conjugation

598 Inner product 性質 (a) (f 1, f 2) = (f 2, f 1)* *: conjugation (b) (k f 1, f 2) = k (f 1, f 2), k 為 scalar (或稱為constant) (c) (f, f) = 0 if and only if f = 0, (f, f) > 0 if and only if f 0, (d) (f 1 + f 2 , g) = (f 1, g) + (f 2 , g) discrete case 亦有這些性質
![599 2 orthogonal on an interval a b f 1 f 2 為 real 599 (2) orthogonal on an interval [a, b] (f 1, f 2 為 real](https://slidetodoc.com/presentation_image_h2/dc4894f5d5e108523f879525faf3cf26/image-6.jpg)
599 (2) orthogonal on an interval [a, b] (f 1, f 2 為 real 時) (more standard definition) 或 比較: discrete case 例子: 當 [a, b] = [-1, 1], 1 和 xk (k 為奇數) 互為 orthogonal 注意:任何 even function 和任何 odd function 在 [-a, a] 之間必為 orthogonal, 包括 Example 1 (text page 426) 的 x 2 和 x 3 在 [-1, 1] 之間也是 orthogonal

600 (3) orthogonal set 有一組 functions 0(x), 1(x), 2(x), 3(x), ………. . 若 for any m n 則 0(x), 1(x), 2(x), 3(x), ………. . 被稱作 orthogonal set on an interval [a, b]

Example 2 (text page 426) Show that the set {1, cosx, cos 2 x, cos 3 x, …. . } is an orthogonal set on the interval [− , ] when one of the functions is 1 when both the two functions are not 1 601

602 (4) square norm 比較: discrete case (5) norm (6) orthonormal set 對一個 orthogonal set, 若更進一步的滿足 for all n 則被稱為 orthonormal set

603 Example 3 (text page 427) Calculate the norms of {1, cosx, cos 2 x, cos 3 x, …. . } 運用三角函式公式 {1, cosx, cos 2 x, cos 3 x, …. . } normalization as a orthonormal set

604 (7) normalize 將 norm 變為 1 (x) 注意,此時 可藉由 normalization, 將 orthogonal set 變成 orthonormal set
![605 8 complete 若在 interval a b 之間任何一個 function fx 都可以表 示成 0x 1x 605 (8) complete 若在 interval [a, b] 之間,任何一個 function f(x) 都可以表 示成 0(x), 1(x),](https://slidetodoc.com/presentation_image_h2/dc4894f5d5e108523f879525faf3cf26/image-12.jpg)
605 (8) complete 若在 interval [a, b] 之間,任何一個 function f(x) 都可以表 示成 0(x), 1(x), 2(x), 3(x), ………. . 的 linear combination 則 0(x), 1(x), 2(x), 3(x), ………. . 被稱作 complete 比較:在 linear algebra 當中,對 3 -D vector 而言 e 1 = [1, 0, 0], e 2 = [0, 1, 0], e 3 = [0, 0, 1] 為 complete Any 3 -D vector [a, b, c] can be expressed as ae 1 + be 2 + ce 3

606 (9)(10) 若 0(x), 1(x), 2(x), 3(x), ………. . 為complete 可將 f(x) 表示成 被稱作 (9) orthogonal series expansion 當 0(x), 1(x), 2(x), 3(x), ………. . 不為 orthogonal, cn 不易算 當 0(x), 1(x), 2(x), 3(x), ………. . 為 orthogonal cn 被稱作 (10) generalized Fourier series

當 0(x), 1(x), 2(x), 3(x), ………. . 為 orthonormal 607

608 11. 1. 3 Orthogonal with Weight Function (11) inner product with weight function 其中 w(x) 被稱作 weight function 加上了 weight function 後 (11 -1) orthogonal 的定義改成 for m n (11 -2) square norm 的定義改成

609 (11 -3) norm 的定義改成 (11 -4) orthonormal 的定義改成 for m n (11 -5) normalize 的算法改成

610 (11 -6) orthogonal series expansion of f(x) 以及 generalize Fourier series 的算法改成

611 11. 1. 4 三角函數表 (要複習) cos(a + b) cosa cosb − sina sinb sin(a + b) sina cosb + cosa sinb cos(a − b) cosa cosb + sina sinb sin(a − b) sina cosb − cosa sinb cosa cosb [cos(a + b) + cos(a − b)]/2 sina sinb [cos(a − b) − cos(a + b)]/2 sina cosb [sin(a + b) + sin(a − b)]/2

612 cos(2 a) cos 2 a − sin 2 a or 1 − 2 sin 2 a or 2 cos 2 a − 1 sin(2 a) 2 sin a cos 2 a [cos(2 a) + 1]/2 sin 2 a [1 − cos(2 a)]/2


614 複習: Legendre polynomials 是一種 orthogonal set if m n 其他常用的 orthogonal set Hermite polynomials (with weight function) (補充) Chebyshev polynomials (with weight function) (補充) Cosine series Sine series Fourier series

615 Section 11. 2 Fourier Series 11. 2. 1 綱要 trigonometric functions orthogonal set on the interval of [ p , p] be proved on pages 620~622 週期: 頻率:


617 (3) 名詞 trigonometric function (page 620) Fourier series (trigonometric series) (page 624) Fourier coefficients (page 624) fundamental period (page 629) period extension (page 629) partial sum (page 631)


619 「頻率」 (frequency) 是個常用字,以 Hz (每秒多少個週期)為單位 說話聲音: 100~1200 Hz 人耳可聽見的聲音: 20~20000 Hz 廣播 (AM): 5× 105 ~ 1. 6× 106 Hz 廣播 (FM): 8. 8× 107 ~ 1. 08× 108 Hz 無線電視: 7. 6× 107 ~ 8. 8× 107, 1. 74× 108 ~ 2. 16× 108 Hz 行動通訊: 5. 1× 108 Hz ~ 2. 75 × 1011 Hz 可見光: 4× 1014 Hz ~ 8 × 1014 Hz 測量頻率的方式: Fourier series Fourier transform

11. 2. 2 Trigonometric Functions trigonometric functions Trigonometric functions is orthogonal on the interval of [ p , p] 要用 + 2 = 5 次的inner products 來證明 (1) 1 VS. Cosine (2) 1 VS. Sine 620

621 (3) Cosine VS. Sine (when h k) when (h = k)

622 (4) Cosine VS. Cosine, k h when h k (5) Sine VS. Sine, k h when h k

623 Square norms of trigonometric functions

624 11. 2. 3 Fourier Series The Fourier series is the orthogonal series expansion (see page 606) by trigonometric functions (Fourier series又被稱作 trigonometric series) The Fourier Series of a function f(x) defined on the interval [ p, p] a 0, an, bn 被稱作 Fourier coefficients

Example 1 (text page 433) 625

626 p=

627 11. 2. 4 Conditions for Convergence 其實未必成立 If (1) f 1(x 0) = f(x 0) if f(x) is continuous at x 0

628 (2) Example 1 的例子 Fig. 11 -2 -1 if f(x) is not continuous at x 0

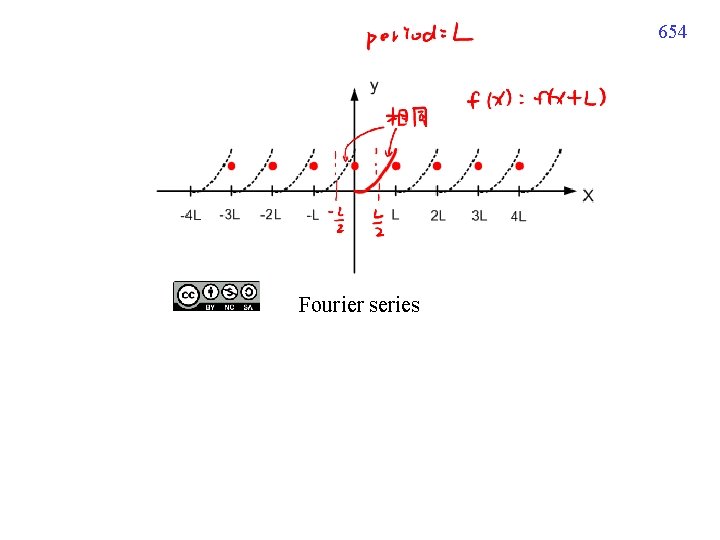
629 11. 2. 5 Period Extension fundamental period: 2 p 在 interval x [ p, p] 以外的地方 (period Extension) f 1(x) 是個週期為 2 p 的 函式 (這是 f 1(x) 和 f(x) 第二個 不同的地方


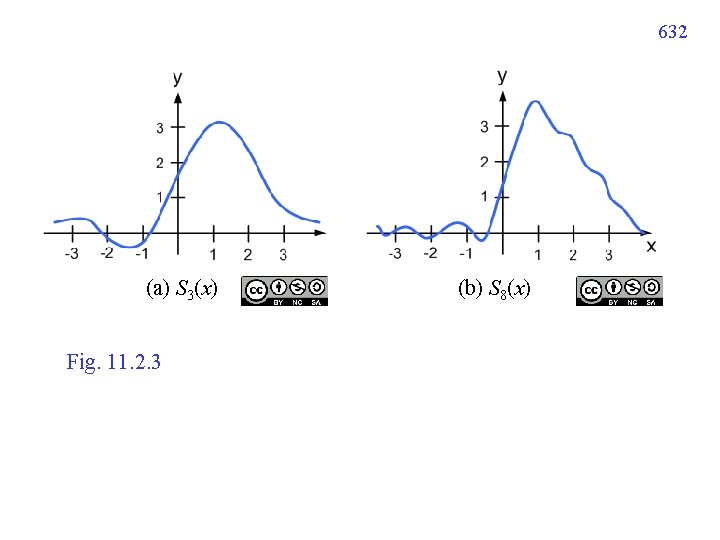
11. 2. 6 Sequence of Partial Sums N 越大,越能逼近原來的 function 631

632 (a) S 3(x) Fig. 11. 2. 3 (b) S 8(x)

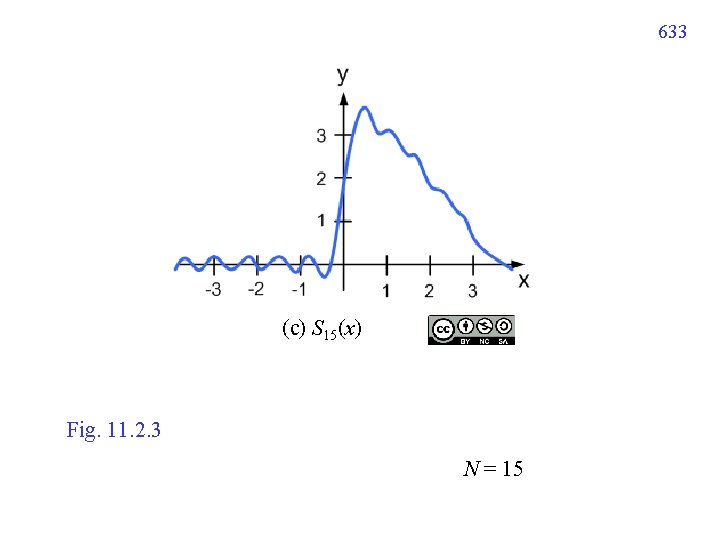
633 (c) S 15(x) Fig. 11. 2. 3 N = 15




637 Section 11. 3 Fourier Cosine and Sine Series 11. 3. 1 綱要 (1) f(x) is even Fourier cosine series (或 cosine series) Fourier Series 比較 page 637 和 page 616 f(x) is odd Fourier sine series (或 sine series)

(2) 重要名詞: Fourier cosine series, cosine series (page 643) Fourier sine series, sine series (page 644) Gibb’s Phenomenon (page 647) 638 (3) Half-range extension: [0, L] (a) cosine series: f(x) = f(−x), interval is changed into [−L, L], set p = L (b) sine series: f(x) = −f(−x), interval is changed into [−L, L ], set p = L (c) Fourier series: (i) interval [−p, p] is replaced by [0, L], (ii) p is replaced by L/2 (4) One of the applications: Solving particular solution (See page 657)

639 11. 3. 2 Even and Odd Functions even function: f(x) = f( x) odd function: f(x) = f( x) Example 1, x 2, x 4, x 6, x 8 …. . are even x, x 3, x 5, x 7, x 9…. . are odd

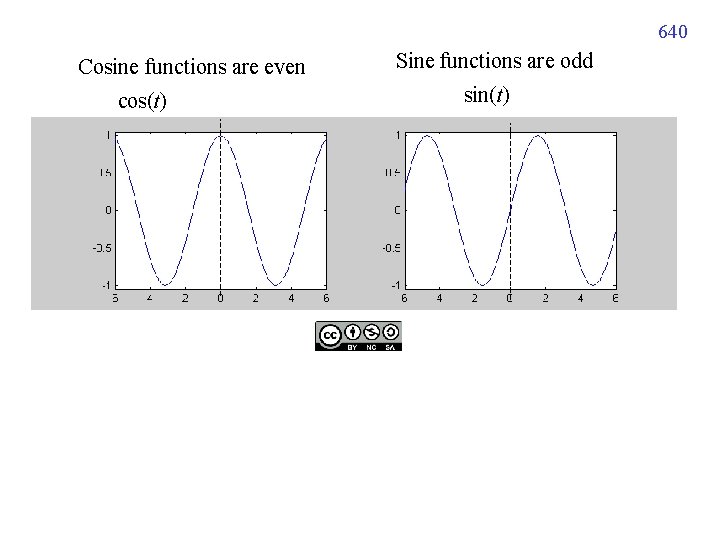
640 Cosine functions are even cos(t) Sine functions are odd sin(t)

Several properties about even and odd functions (a) The product of two even functions is even 例: x 2 x 4 = x 6 (b) The product of two odd functions is even 例: x x = x 2 (c) The product of an even function and an odd function is odd 例: x x 2 = x 3 (d) The sum (or difference) of two even function is still even (e) The sum (or difference) of two odd function is still odd 641

642 (f) If f(x) is even, then (g) If f(x) is odd, then (Proof): (令 x 1 = −x, dx 1 = −dx) When f(x) = f(−x) When f(x) = − f(−x)

11. 3. 3 Fourier Cosine and Sine Series (1) The Fourier series of an even function on the interval (−p, p) is the cosine series (或稱作 Fourier cosine series) 和之前 Fourier series 不一樣的地方有三個 適用情形: (1) f(x) is even (2) Half range extension (page 649) 643

644 (2) The Fourier series of an odd function on the interval (−p, p) is the sine series (或稱作 Fourier sine series) 和之前 Fourier series 不一樣的地方有三個 (是哪三個) 適用情形: (1) f(x) is odd (2) Half range extension (page 649)

645 Example 1 (text page 438) Expand f(x) = x, 2 < x < 2 in a Fourier series f(x) is odd expand f(x) by a Fourier sine series Fig. 11. 3. 3

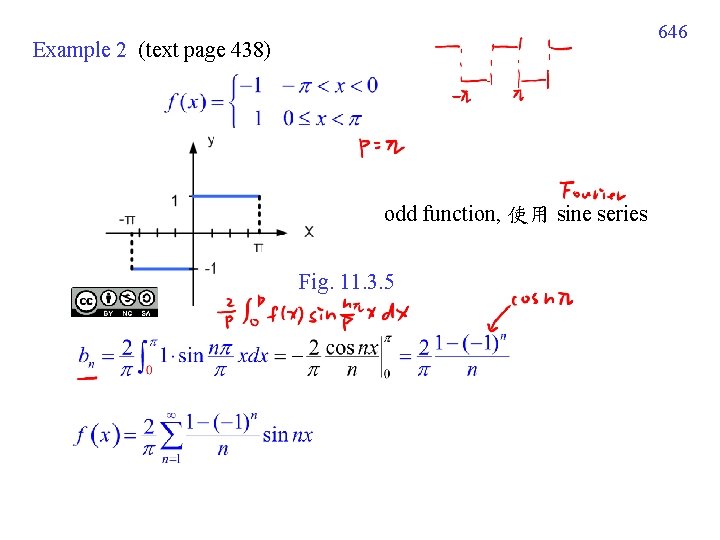
646 Example 2 (text page 438) odd function, 使用 sine series Fig. 11. 3. 5

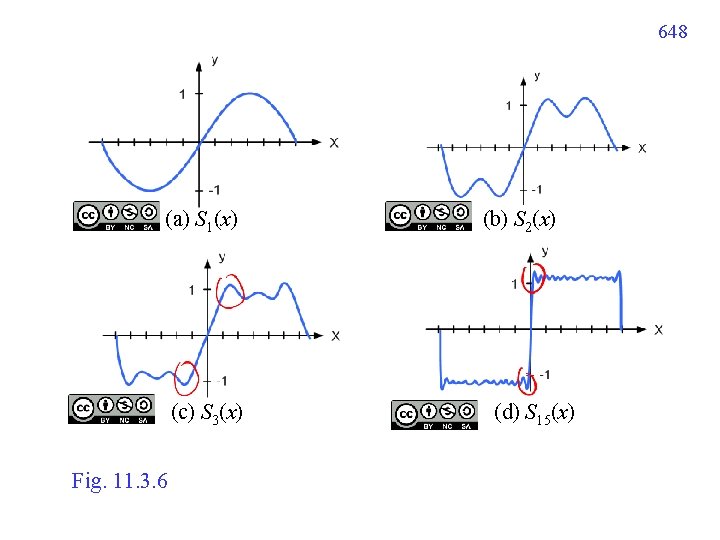
11. 3. 4 Gibbs Phenomenon Example 2 的結果 partial sum 當 N 不為無限大,在 discontinuities 附近會有 “overshooting” 的大小不會隨著 N 而變小 但寬度會越來越窄,越來越靠近 discontinuities 的地方 這種現象,稱作 Gibb’s phenomenon 647

648 (a) S 1(x) (c) S 3(x) Fig. 11. 3. 6 (b) S 2(x) (d) S 15(x)

11. 3. 5 Half Range Extension 649 之前的例子: f(x) is defined in the interval of −p < x < p 若問題改成 Expand f(x), 0 < x < L (f(x) 只有在 0 < x < L 當中有定義) (a) In a cosine series (i) Interval: [−L, L], (ii) 所有公式的 p 由 L 取代, (iii) 結果是 even (b) in a sine series (i) Interval: [−L, L], (ii) 所有公式的 p 由 L 取代 , (iii) 結果是 odd (c) in a Fourier series (i) Interval: [0, L], (ii) 所有公式的 p 由 L/2 取代

650 如 Example 3 (text page 440), f(x) = x 2, 0<x<L (a) in a cosine series 假設 f(x) = f( x) for −L < x < 0, (假設 f(x) 是一個 even function) interval變為 ( L, L) 原本 cosine series 公式 現在只不過將 p 改成 L

651 (b) in a sine series 假設 f(x) = f( x) for −L < x < 0, (假設 f(x) 是一個 odd function) interval 變為 ( L, L) 原本 sine series 公式 現在只不過將 p 改成 L

(c) in a Fourier series interval 仍為 (0, L) 原本 Fourier series 公式 現在 (1) 將 interval [−p, p] 換為 [0, L], (2) 將 p 換為 L/2 652

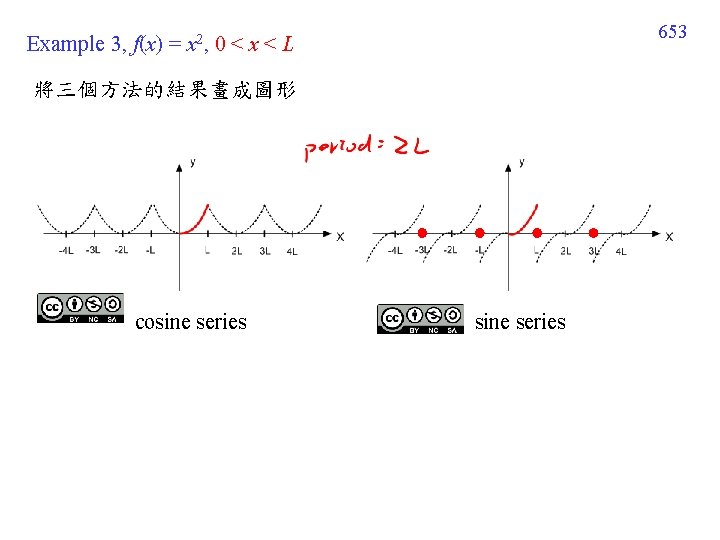
653 Example 3, f(x) = x 2, 0 < x < L 將三個方法的結果畫成圖形 cosine series

654 Fourier series

11. 3. 6 Solving Particular Solutions (第四個方法) 方法的限制 (註:以下的步驟不包含解 homogeneous solution 還是需要用 Section 4 -3 的方法來解) (Step 1) 將 f(t) 表示成 Fourier series 或 cosine series (當 f(t) 為 even) 或 sine series (當 f(t) 為 odd) 655

(Step 2) 假設 particular solution 的型態為 (Step 3) 代回原式,比較係數,將 A 0, An, Bn 解出來 若所假設的 particular solution 和 homogeneous solution 有相同的地方,則要乘上 t 656

657 Example 4 (text page 441) (相關物理定理請複習 Section 5. 1) for 1 < t < 1 Step 1 假設 (因為 f(t) 是 odd)


659 Step 3 將 xp(t) 和 Step 1 的結果代入 Therefore, the particular solution is:


11. 3. 7 Section 11. 3 需要注意的地方 (1) 公式一些地方易記錯 for cosine series and sine series, (2) Fourier series 的 half-range extension 和 cosine series 及 sine series 不同 p is replaced by L/2, [−p, p] is replaced by [0, L] (3) Half range extension 和 solving particular solution 這兩個部分 較複雜,需要特別注意,並且多練習例題 661

662 Exercise for Practice Section 11 -1 3, 5, 6, 8, 13, 14, 17, 19, 20, 21, 22, 23 Section 11 -2 2, 5, 9, 10, 12, 16, 19, 22, 23, 24 Section 11 -3 14, 16, 18, 21, 22, 23, 28, 29, 33, 36, 37, 43, 46, 47 a, 48 a, 49, 52 Review 11 6, 12, 13, 14, 15, 17, 18

663 Chapter 14 Integral Transform Method Integral transform 可以表示成如下的積分式的 transform kernel Laplace transform is one of the integral transform 本章討論的 integral transform: Fourier transform


Section 14. 3 Fourier Integral 14. 3. 1 綱要 (1) Fourier integral: (和 Fourier series 的定義比較) 665

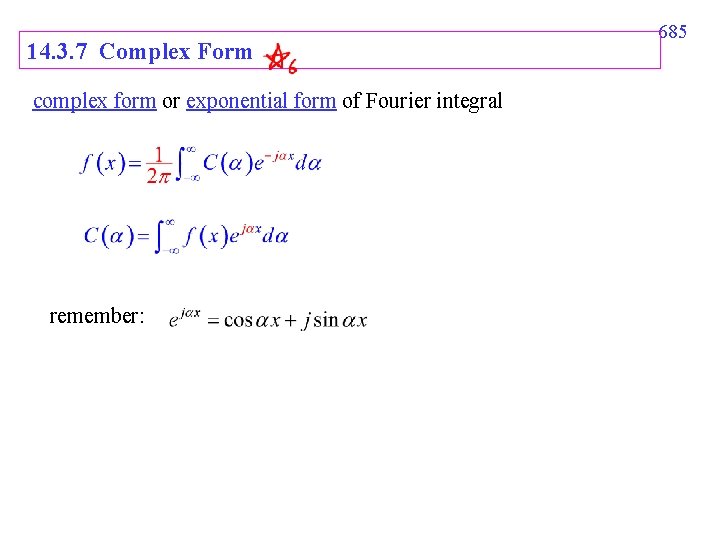
(2) complex form 或 exponential form of Fourier integral 比較: Fourier integral 原本的定義 666

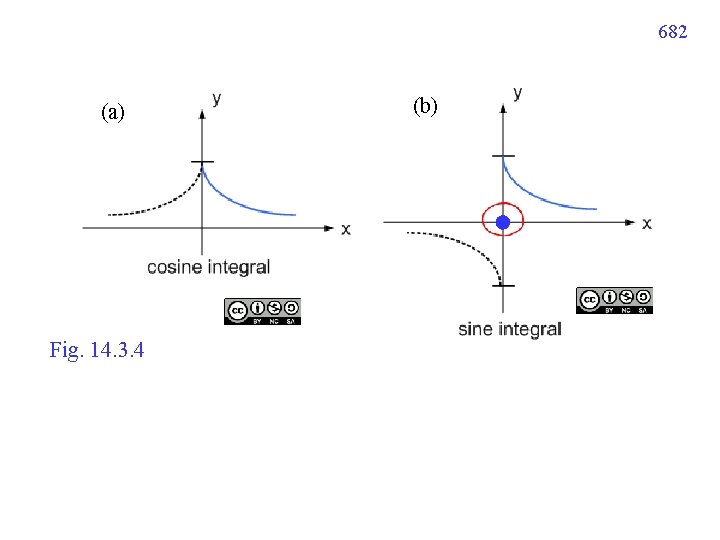
(3) Fourier cosine integral 或 cosine integral 適用情形: (1) even 或 (2) interval: [0, ) (4) Fourier sine integral 或 sine integral 適用情形: (1) odd 或 (2) interval: [0, ) (5) Others 名詞:absolutely integrable (page 671) partial integral (page 683) 特殊公式: 667

14. 3. 2 From Fourier Series to Fourier Integral 複習:Section 11 -2 的 Fourier series: 668



14. 3. 3 Fourier Integral: Fourier integral 存在的 sufficient condition: converges 若這個條件滿足,f(x) 為 absolutely integrable 671


Theorem 14. 3. 1 Condition for convergence When (1) f(x) 為 piecewise continuous (2) f (x) 為 piecewise continuous (3) f(x) 為 absolutely integrable The Fourier integral of f(x) (即上一頁的 f 1(x)) converges to f(x) at a point of continuity. At the point of discontinuity, f 1(x) converges to 673

Example 1 (text page 531) Find the Fourier integral representation of f(x) 674


14. 3. 4 Fourier Transform 意外的提供了一些方程式積分的 算法 由 Example 1 When x = 1, since f(x) = 1 676

677 補充: sinc function 的定義: 常用在 sampling theory, filter design, 及通訊上

14. 3. 5 Fourier Cosine and Sine Integrals 678 (A) Fourier cosine integral 或 cosine integral 注意:有三個地方和 Fourier integral 不同 (1) 類比於 cosine series (2) (3) 適用情形: (1) f(x) is even, f(x) = f(−x) (2) 只知道 f(x) 當 x > 0 的時候的值 (類似於Section 11. 3 的 half-range expansion, 而且假設 f(x) = f(−x) )

679 (B) Fourier sine integral 或 sine integral 類比於 sine series 適用情形: (1) f(x) is odd, f(x) = −f(−x) (2) 只知道 f(x) 當 x > 0 的時候的值 (類比於Section 11. 3 的 half-range expansion, 而且假設 f(x) = −f(−x) )

Example 3 (text page 533) Represent (a) by a cosine integral (b) by a sine integral Solution: (a) Suppose that (其實,有一個取巧的快速算法,用 Laplace transform) 680

cosine integral: (b) 681

682 (a) Fig. 14. 3. 4 (b)

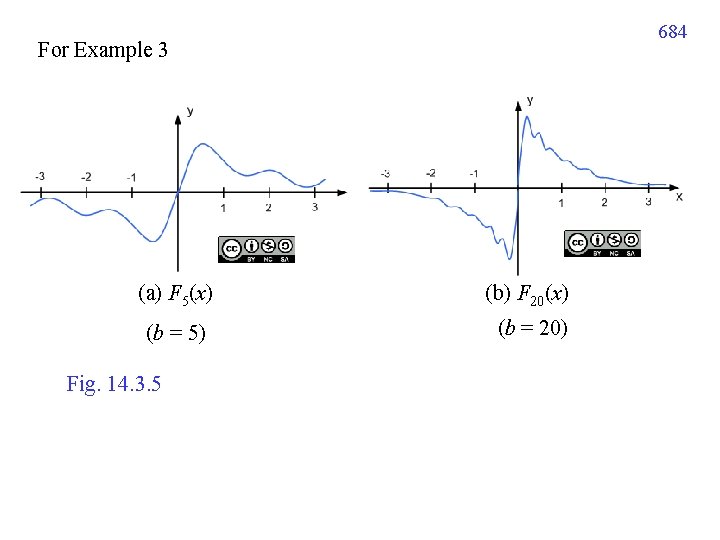
683 14. 3. 6 Partial Integral partial integral for Fourier integral partial integral for cosine integral partial integral for sine integral (用 b 取代 )

684 For Example 3 (a) F 5(x) (b) F 20(x) (b = 5) (b = 20) Fig. 14. 3. 5

14. 3. 7 Complex Form complex form or exponential form of Fourier integral remember: 685

686 Proof: 由講義 page 671 Fourier integral 的定義 注意: 對 而言是 even function

687 From (因為 對 而言是 odd function)

688 14. 3. 8 Section 14. 3 需要注意的地方 (1) 公式積分的外面,要乘 (Fourier integral) 或 (Complex form of Fourier integral) 或 (cosine integral, sine integral) (2) 一些積分的計算會常常用到 算法:假設解為 或者用 Laplace transform 的公式, s = 1

Section 14. 4 Fourier Transforms 689 14. 4. 1 綱要 Fourier transform,其實就是 complex form of Fourier integral 公式: 代表 Fourier transform 本節著重於 (1) 定義 (2) 性質 學習方式:多和 Laplace transform 比較 (3) Solving the boundary value problem (pages 703713) 有一點複雜,且常考,要勤於練習

690 (A) 六大定義 (1) Fourier transform (2) inverse Fourier transform (3) Fourier sine transform (4) inverse Fourier sine transform (5) Fourier cosine transform (6) inverse Fourier cosine transform 注意:除了 ej x 變成 cos( x) 以外 還有三個地方和 Fourier transform 不同

691 (B) 微分性質 (7) for Fourier transform (8) (9) for Fourier sine transform 不同 (10) (11) for Fourier cosine transform 不同 (12)

(C) Problems with boundary conditions (多練習) (13) 可考慮用 Fourier transform 的情形 (14) 可考慮用 Fourier sine transform 的情形 when x = 0 (15) 可考慮用 Fourier cosine transform 的情形 另外,要熟悉 page 704 的計算流程 (D) 名詞 transform pair (page 693) heat equation (page 705) 692

693 14. 4. 2 Transform Pair Transform pair 的定義: 若 甲 A 乙 乙 則 A 和 B 形成一個 transform pair 甲和乙 B 甲

694 14. 4. 3 Fourier Transform Fourier transform pair 和之前 complex form of Fourier integral 相比較 只不過把 C( ) 換成 F( ) 為何要取兩個名字? ? ? Fourier transform 存在的條件 (1) (absolutely integrable) (2) f(x) and f (x) 為 piecewise continuous

695 Fourier transform 和 Laplace transform 之間的關係: 把 s 換成 −j Laplace:

14. 4. 4 Fourier Sine Transform and Fourier Cosine Transform Fourier sine transform pair Fourier cosine transform pair Fourier sine / cosine transform 存在的條件 (1) (absolutely integrable) (2) f(x) and f (x) 為 piecewise continuous 696

Fourier sine / cosine transform 的意義: (1)當 f(x) 為 even Fourier transform Fourier cosine transform 等於 0 for Fourier cosine transform 697

698 (2) Inverse Fourier transform inverse Fourier cosine transform If f(x) is even (由前頁) 由於對 Fourier cosine transform 而言 (even function ) 等於 0

Fourier cosine transform 等同於 Fourier transform 當 input f(x) 為 even 的情形。當 f(x) 為 even, Fourier sine transform 等同於 Fourier transform 當 input f(x) 為 odd 的情形。當 f(x) 為 odd, 然而,若 f(x) 只有在 x [0, ) 之間有定義,也可以用 Fourier cosine / sine transform (類似於Section 11. 3 的 half-range expansion) 699

14. 4. 5 微分性質 (1) Fourier transform 的微分性質做了一些假設: f(x) = 0 when x and x 以此類推 比較:對 Laplace transform 對 Fourier transform s −j , without initial conditions 700

(2) Fourier sine transform 的微分性質 (3) Fourier cosine transform 的微分性質 注意: (1) Fourier sine, cosine transforms 互換 (2) 正負號不同 (3) Fourier cosine transform 要考慮 initial condition 701
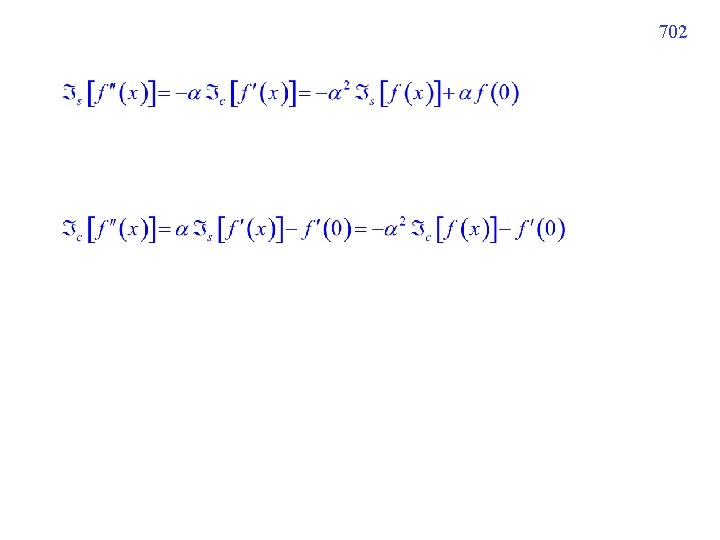
702

14. 4. 6 Solving the Boundary Value Problem (BVP) 703 ※ 概念複雜,要特別加強練習 (Condition 1) interval 為 < v < 時: 用 Fourier transform (Condition 2) interval 為 0 < v < , 有 “u(v, …. . ) = 0 or a constant when v = 0” 的 boundary condition 時 : 用 Fourier sine transform (Condition 3) interval 為 0 < v < , 有“ 時: or a constant when v = 0” 的 boundary condition 用 Fourier cosine transform

使 用 Fourier transform, Fourier cosine transform, Fourier sine transform 來解 partial differential equation (PDE) 的 BVP 或IVP 的解法流程 (Step 1) 以 page 703 的規則,來決定要針對 哪一個 independent variable ,做什麼 transform (Fourier, Fourier cosine, 或Fourier sine transform) (Step 2) 對 PDE 做 Step 1 所決定的 transform, 則原本的 PDE 變成 針對另外一個 independent variable 的 ordinary differential equation (ODE) (Step 3) 將 Step 2 所得出的 ODE 的解算出來 (Step 4) Step 3 所得出來的解會有一些 constants,可以對 initial conditions (或 boundary conditions) 做 transform 將 constants 解出 (※ 和 Step 1 所做的 transform 一樣,只是 transform 的對象變成 是 initial 或 boundary conditions,見 pages 705, 708 的例子) (Step 5) 最後,別忘了做 inverse transform (畫龍點睛) 704

705 Example 1 (text page 538) heat equation: subject to where Step 1 決定針對 x 做 Fourier transform Step 2 原本對 x, t 兩個變數做偏微分 經過 Fourier transform 之後, 只剩下對 t 做偏微分

706 對於 t 而言,是 1 st order ODE 這邊的 c 值,對 t 而言是 constant , Step 3 但是可能會 dependent on (特別注意) Step 4 根據 u(x, 0) = f(x) 將 c 解出 和 Step 1 一樣,也是針對 x 做 Fourier transform 只是對象改成 initial condition 因為


Example 3 Laplace’s equation (text page 540) Step 1 決定針對 y 做 Fourier cosine transform Step 2 from 對於 x 的 2 nd order ODE 708


710 Step 4 由 來解 c 1, c 2 和 Step 1 一樣,也是針對 y 做 Fourier cosine transform 只是對象改成 boundary conditions (1 ) (2 ) 分別代入 (1 ) (2 ) (可以用Laplace transform 的「取巧法」 )

711 Step 5 inverse cosine transform (算到這裡即可,難以繼續化簡)

14. 4. 7 Section 14. 4 需要注意的地方 712 (1) 微分公式當中,Fourier cosine transform 和 Fourier sine transform 會 有互換的情形。(See pages 701, 702) (2) 公式會有很多小地方會背錯 (特別注意綱要的公式中紅色的地方) (3) 在解 boundary value problem 時,要了解 何時用 Fourier transform, 何時用Fourier cosine transform, 何時用 Fourier sine transform (see page 703) (4) 解 boundary value problem 流程雖複雜,但只要記住, 方法的精神,在於: 運用 transform, 將原本針對兩個以上 independent variables 做微分的 PDE, 變成只有針對一個 independent variable 做微分的 ODE

713 (5) 在解 partial differential equation 時,往往只針對一個 independent variable 做 Fourier transform, 另一個 independent variable 不受影響, 如 Examples 1 and 2, pages 705 and 708 的例子 計算過程中,自己要清楚是對哪一個 independent variable 做Fourier transform ※ 本人習慣用下標做記號 (建議同學們使用) (6) Step 4 和 Step 1 必需是針對同一個 independent variable 來做 同一種 transform,只是處理的對象改成了 initial (or boundary) conditions (see pages 706, 710) (7) 注意 page 709, 有時我們會用 來取代 ,以方便計算



716 Exercise for Practice Section 14 -3 3, 4, 7, 12, 15, 16, 17, 19, 20 Section 14 -4 1, 2, 3, 9, 12, 15, 16, 18, 19, 20, 21, 27 Review 14 2, 7, 8, 11, 15, 16
 Orthogonal functions and fourier series
Orthogonal functions and fourier series Fourier series and orthogonal functions
Fourier series and orthogonal functions Orthogonal functions in fourier series
Orthogonal functions in fourier series Fourier series and integrals
Fourier series and integrals Orthogonal series expansion
Orthogonal series expansion Orthogonal polynomials examples
Orthogonal polynomials examples Trigonometric form of fourier series
Trigonometric form of fourier series Site:slidetodoc.com
Site:slidetodoc.com Half range fourier sine series formula
Half range fourier sine series formula Upenn cit
Upenn cit Iri zahlen pikas
Iri zahlen pikas 86 è divisibile per
86 è divisibile per Cit 594
Cit 594 841*594
841*594 Mcit 594
Mcit 594 Magni 599
Magni 599 Ai 594
Ai 594 Upenn cis courses
Upenn cis courses Cis classes upenn
Cis classes upenn Com(2020) 594 final
Com(2020) 594 final Fourier
Fourier Series de fourier
Series de fourier Serie de fourier
Serie de fourier Frequency domain to time domain
Frequency domain to time domain Frequency differentiation property of fourier transform
Frequency differentiation property of fourier transform Fourier transform of a periodic function
Fourier transform of a periodic function Half-wave symmetry examples
Half-wave symmetry examples Use of fourier series
Use of fourier series Fourier transform of impulse train
Fourier transform of impulse train Rectified sine wave fourier series
Rectified sine wave fourier series Fourier transform formula
Fourier transform formula Parseval's theorem
Parseval's theorem Fourier series coefficients
Fourier series coefficients Polar fourier series
Polar fourier series Fourier series multiplication property
Fourier series multiplication property Fourier series representation
Fourier series representation Properties of fourier transform
Properties of fourier transform Fourier
Fourier Fourier series
Fourier series Fourier's theorem
Fourier's theorem Half range fourier series formula
Half range fourier series formula Discrete time fourier series
Discrete time fourier series Discrete fourier transform
Discrete fourier transform Dtft representation of
Dtft representation of Fourier series circuit analysis
Fourier series circuit analysis Inverse fourier transform of delta function
Inverse fourier transform of delta function Series complejas de fourier
Series complejas de fourier Matlab fourier series coefficients
Matlab fourier series coefficients Series fourier
Series fourier Series de fourier
Series de fourier Parseval's theorem in signals and systems
Parseval's theorem in signals and systems Fourier series
Fourier series Series de fourier
Series de fourier Series de fourier
Series de fourier Fourier
Fourier Fourier series coefficients formula
Fourier series coefficients formula Wolfram fourier series
Wolfram fourier series What is fourier series
What is fourier series Rayleigh energy theorem
Rayleigh energy theorem Step function fourier transform
Step function fourier transform Fourier series formula
Fourier series formula Transformata fourier
Transformata fourier Fourier transform in polar coordinates
Fourier transform in polar coordinates Fourier series
Fourier series Fourier series of periodic function
Fourier series of periodic function Single phase half wave controlled rectifier with rle load
Single phase half wave controlled rectifier with rle load Series aiding and series opposing
Series aiding and series opposing Sinc fourier transform
Sinc fourier transform Fourier transform of product of two functions
Fourier transform of product of two functions Kl transform example
Kl transform example Maclaurin series vs taylor series
Maclaurin series vs taylor series Heisenberg 1925 paper
Heisenberg 1925 paper Taylor vs maclaurin
Taylor vs maclaurin Taylor vs maclaurin
Taylor vs maclaurin Ibm p series server
Ibm p series server Shunt series amplifier
Shunt series amplifier Arithmetic sequence sum formula
Arithmetic sequence sum formula Ndc computer graphics
Ndc computer graphics Orthonormal basis
Orthonormal basis Orthogonal unit differentiation
Orthogonal unit differentiation Irange tree
Irange tree Example of an orthogonal matrix
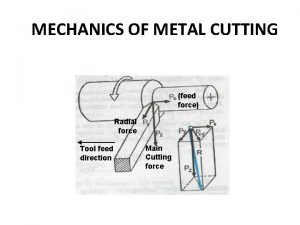
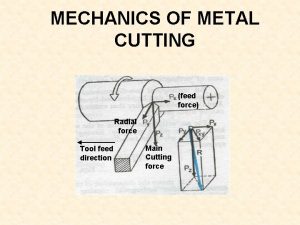
Example of an orthogonal matrix Orthogonal cutting diagram
Orthogonal cutting diagram Orthogonal basis example
Orthogonal basis example Object basics in ooad
Object basics in ooad Feed in metal cutting
Feed in metal cutting What is orthogonal matrix
What is orthogonal matrix Orthogonal iteration
Orthogonal iteration Orthogonal matrix properties
Orthogonal matrix properties Eigenvalue definition
Eigenvalue definition Taguchi l18 orthogonal array
Taguchi l18 orthogonal array Eigenvectors of orthogonal matrix
Eigenvectors of orthogonal matrix Orthogonal decomposition
Orthogonal decomposition Cauchy-schwarz inequality proof inner product
Cauchy-schwarz inequality proof inner product Orthogonal complement
Orthogonal complement Define orthogonal transformation
Define orthogonal transformation Orthogonal transformation
Orthogonal transformation Theory of metal cutting
Theory of metal cutting Pythagoras theorem for orthogonal set of vectors
Pythagoras theorem for orthogonal set of vectors Orthogonal hole phantom
Orthogonal hole phantom Feed force
Feed force Orthogonal projection in computer graphics
Orthogonal projection in computer graphics Isometric drawing characteristics
Isometric drawing characteristics Orthogonal set
Orthogonal set Cartesian equation
Cartesian equation Taguchi design of experiments
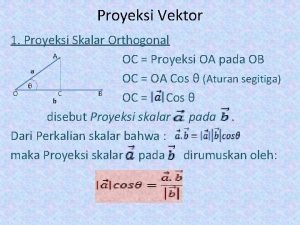
Taguchi design of experiments Proyeksi vektor skalar ortogonal
Proyeksi vektor skalar ortogonal Orthogonal projection
Orthogonal projection Orthogonal
Orthogonal What are the two orthogonal view of software
What are the two orthogonal view of software Long term evolution advanced
Long term evolution advanced Orthogonal matrix
Orthogonal matrix Channel
Channel Lip angle of single point cutting tool
Lip angle of single point cutting tool First order linear differential equation
First order linear differential equation Representations of functions as power series
Representations of functions as power series Evaluating functions and operations on functions
Evaluating functions and operations on functions Evaluating functions and operations on functions
Evaluating functions and operations on functions Chapter 12 sequences and series answers
Chapter 12 sequences and series answers Chapter 23 series and parallel circuits study guide answers
Chapter 23 series and parallel circuits study guide answers Sequences and series math 20-1
Sequences and series math 20-1 Chapter 1 sequences and series
Chapter 1 sequences and series Sequences and series math 20-1
Sequences and series math 20-1 Piecewise functions absolute value
Piecewise functions absolute value